2. 中国气象科学研究院, 北京 100091;
3. 国家气象中心, 北京 100091;
4. 中国气象局北京城市气象研究所, 北京 100142
青藏高原(下称高原)作为“第三极”,对东亚甚至全球的天气和气候影响巨大。早在1979年和1998年,中外科学家们相继完成了第一次和第二次高原大气科学试验(TIPEX)(徐祥徳和陈联寿,2006)。试验得到了许多重要的研究成果,例如: 高原大地形在大气环流中的动力和热力作用(Chen and Luo,2003: Zhang et al,2003: 刘式适等,2000; 卓嘎等,2002; 梁玲等,2013; 郁淑华等,2013); 高原地区边界层复杂的对流机制(周玉淑和邓涤菲,2012; 田红瑛等,2014); 高原的水汽“转运站”功能(Xu et al,2003); 高原和亚洲夏季风的关系(Massimo and Sam,2004; Qie et al,2014)等。由于高原地区复杂的动力和物理过程,数值天气预报(NWP)在高原地区存在较大的模式不确定性,例如: 数值模拟结果对高原的大地形十分敏感(吴国雄等,2005; 何钰和李国平,2013); 参数化的选择对高原的数值预报十分重要(李川等,2006)等。
近年来还开展了一些针对高原地区的观测试验: 从2005年开始的新一代完整的高原观测系统(New Integrated Observational Systems over TP,NIOST); 2012年起发展的高原观测研究平台(Tibetan Observation and Research Platform,TORP)(Ma et al,2008); 第三次高原大气科学试验(TIPEX3)也于近期启动,TIPEX3的一个主要任务即为,在高原及其周边地区建立一个完备的观测系统(李跃清,2011)。然而高原观测资料仍旧十分匮乏,使得对高原的研究十分困难(Xu et al,2008)。而在数值天气预报中,观测资料的缺乏,会增大初始分析场的不确定性。这些初值不确定性,会由大气模式的非线性作用进一步放大,进而导致数值预报误差的增加(Danforth et al,2007)。许多研究(Szunyogh et al,2002; Davies and Marco,2013; Langland et al,2002; Prive et al,2013)表明,这些初始误差能够迅速的传播到下游地区,对下游地区的预报影响显著。
因此,本文通过NCEP全球预报在不同地区的预报误差分析、 包含大地形(亚洲青藏高原、 北美落基山脉)与否的区域模拟试验、 同化高原地区人造观测的观测系统模拟试验,探讨了数值预报在高原地区的不确定性对其下游地区预报的影响,为减少青藏高原下游地区数值预报误差提供可行的策略。
2 全球预报模式(GFS)不同区域预报误差分析数值预报的不确定性主要有两个来源: 初始误差和模式误差。高原由于其复杂的动力、 物理过程和较为稀疏的观测,数值预报在该地区存在较大的不确定性。利用全球数值预报在不同区域的月平均预报误差,分析高原的不确定性对其下游预报的影响。
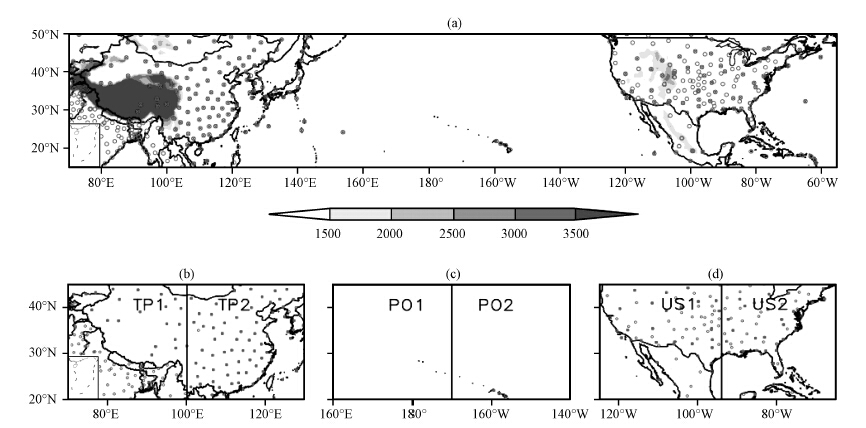
2.1 验证区域设置和资料说明图 1a中给出了常规地面和探空观测站点在中纬度地区的分布,站点位置来源于世界气象组织(WMO)的全球观测系统(2007年7月版本); 其中阴影为复杂地形区: 位于东亚青藏高原和北美西部的落基山脉。从图 1a中可以看出,高原地区的观测较为稀少。为分析复杂地形和观测稀少对其下游预报的影响,将图 1a中的区域分为6个部分(图 1b~d): 包含整个高原大部的高原地形区(简称TP1); 紧邻高原大地形的下游区(TP2); 太平洋西侧地区(PO1); 太平洋东侧地区(PO2); 包含北美落基山脉大地形地区(US1); 落基山脉下游地区(US2)。表 1中给出了各个区域设置的详细说明。
|
图 1 常规观测站分布(a)和验证区域设置(b~d) 空心圆为常规地面观测站点,十字为探空观测站点,阴影为地表高度(单位: m).(b)TP1和TP2,(c)PO1和PO2,(d)US1和US2 Figure 1 The distribution of observing stations(a)and verification region setup(d~d).Hollow cycles is the surface stations.Cross is the upper-air stations.The shaded is the terrain height(unit: m).(b)TP1 and TP2,(c)PO1 and PO2,(d)US1 and US2 |
本文利用美国环境预报中心NCEP(National Center for Environmental Prediction)全球模式GFS(Global Forecast System)24 h和48 h预报的500 hPa高度场进行研究分析。预报资料的起始时间为2012年7月1-31日00:00(世界时,下同),水平分辨率为1°×1°。每天24 h和48 h预报相对于分析的均方根误差计算公式为
| 表 1 检验区域设置 Table 1 The configuration of the verification region |
| $RMSE=\sqrt{\frac{1}{N}\sum _{i=1}^{N}{{\left( {{f}_{i}}-{{a}_{i}} \right)}^{2}}},$ | (1) |
其中: f表示24 h或48 h的GFS 500 hPa高度场预报。a表示对应时次的分析场。N为验证区域内的格点总数。所有计算基于DTC(Developmental Testbed Centre)的MET(Model Evaluation Tools)系统,版本为4.0。
2.2 结果分析表 2给出了500 hPa高度场的24 h和48 h预报的月平均均方根误差。从表 2中可以看出,在积分初始阶段(前24 h),由于高原复杂的地形和观测资料的缺乏,TP1的均方根误差最大; 其下游不同地区的预报误差自上游向下游(或自西向东)呈阶梯式减小,远离高原的太平洋中部地区的预报误差最小; 在积分48 h以后,各个检验地区的预报误差都有所增加,但紧邻高原的TP2地区预报误差增长率最为显著(约为0.77),大于其它地区(约为0.55)。对比同为大地形的落基山脉地区: TP1的24 h预报误差大于TP2、 US1和US2,而TP2和US1、 US2的误差相当,均在5.7 gpm左右; 然而,在模式积分48 h以后,TP2的预报误差迅速增加,超过TP1,在所有验证区中达到最大。这说明在积分初始阶段(前24 h)高原地区的预报误差较大(预报存在较大的不确定性),这种不确定的预报在积分48 h后,会使得紧邻高原下游地区的预报误差迅速增大。
| 表 2 不同检验地区500 hPa高度场月平均均方根误差 Table 2 The monthly average RMSE of 500 hPa geopotential height at different verification region |
数值模式的误差增长主要来源有: 模式非线性作用对初始误差的放大; 模式自身不足(对大地形的处理; 参数化方案的不足等)。而高原地区由于缺乏观测,初始误差较大,因此随着数值模式积分,误差的放大作用较其他地区更为明显; 此外,高原地区的动力和热力过程较其他地区更为复杂,这也使得紧邻高原下游地区预报误差迅速增大。
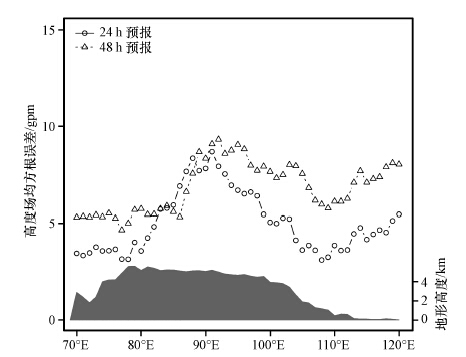
图 2给出了不同预报时效下水平风场,较分析时刻的月平均均方根误差沿着35°N的变化曲线。从图 2中可以看出,结果类似于表 2,紧邻高原的下游地区预报误差较高原地区小; 而在积分48 h后,高原下游地区预报误差迅速增大,其增长速度比高原地区快,其数值和高原地区的均方根误差相当。以上情况说明高原地区预报的不确定性,会影响其下游地区的预报。
|
图 2 500 hPa水平风场24 h和48 h预报的月平均均方根 误差沿35°N的纬向变化曲线 黑色填色区为地面海拔(单位: km) Figure 2 The zonal changing curve of monthly average RMSE of 500 hPa horizontal wind at 24 h forecast and 48 h forecast along 35°N.The black areas are the surface height.Unit: km |
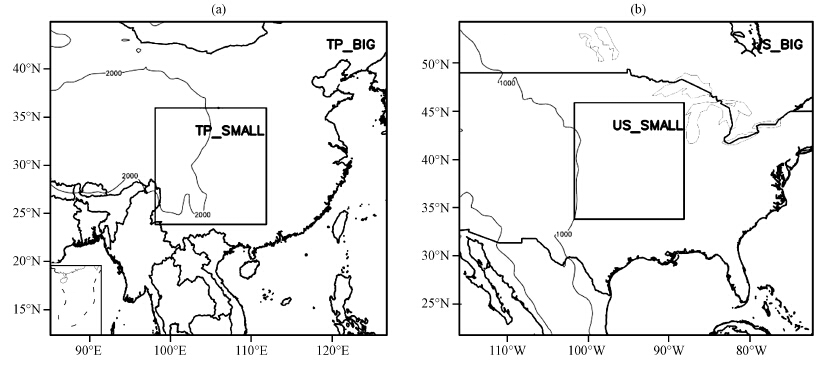
本文使用的区域数值模式为ARW-WRF,版本为3.4.1。设计4个对比试验,分别为TP_BIG、 TP_SMALL、 US_BIG和US_SMALL。四个试验的水平分辨率同为9 km,垂直层为27层,初始和边界条件均由NCEP_GFS的12 h预报场提供,水平分辨率为1°×1°,起报时间为2012年7月6日00:00,预报时效为48 h。区别在其模拟范围(图 3): TP_BIG包含高原及其下游地区,水平格点为500×400; 而TP_SMALL只覆盖紧邻高原的我国西南地区,格点数为140×150; US_BIG覆盖北美大陆大部分地区; 而US_SMALL只包含落基山脉下游部分地区。更多模式配置参数(如格点数、 微物理过程、 边界层方案等)详见表 3。
|
图 3 模拟区域设置 (a)TP_BIG和TP_SMALL,(b)US_BIG和US_SMALL Figure 3 Geographical domains used in TP/US experiments |
| 表 3 模式配置参数 Table 3 The configuration of model parameters |
参与检验的气象要素有500 hPa高度、 温度和水平风分量。其中用于检验的“实况”资料为对应时刻的GFS分析场。检验区域统一为“大地形”的下游即小区域试验(TP_SMALL和US_SMALL)所覆盖地区。
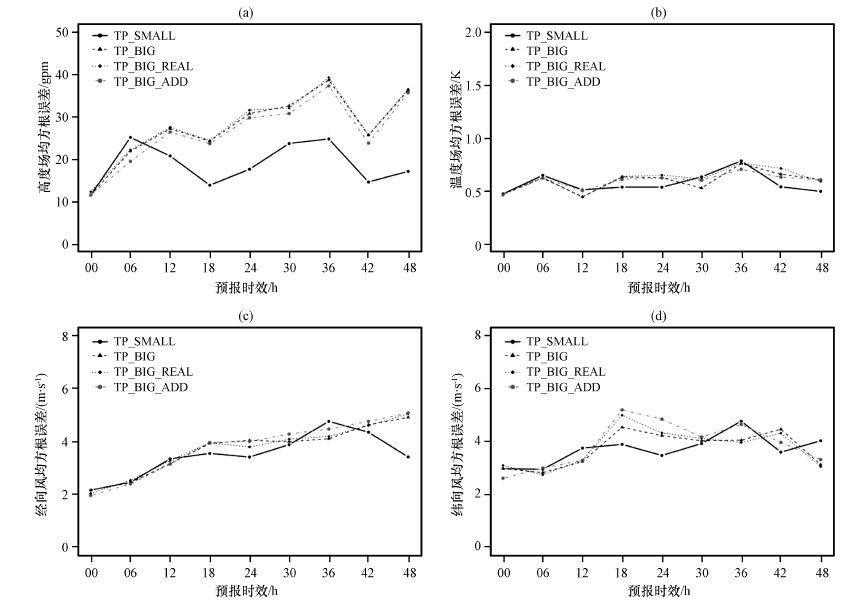
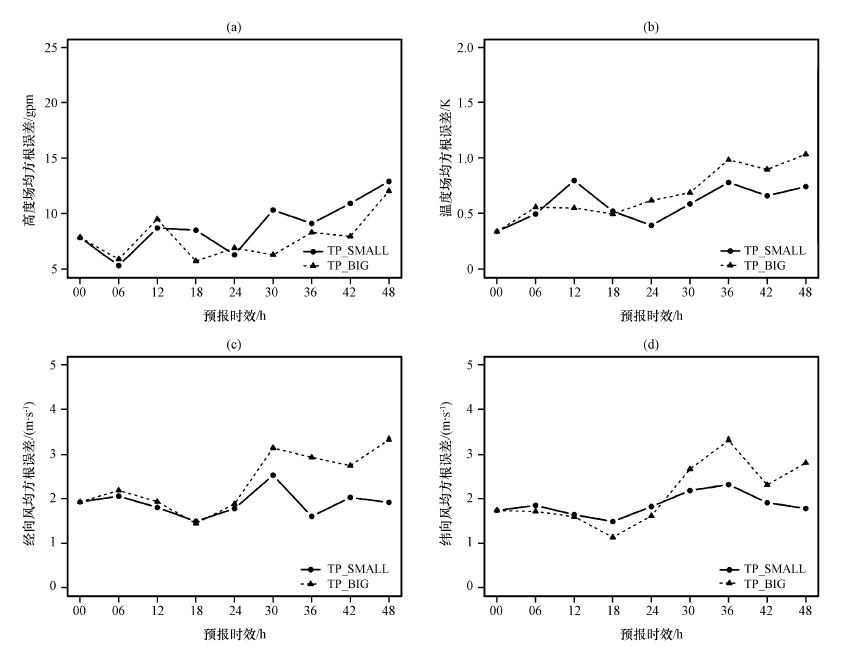
图 4给出了TP_BIG和TP_SMALL不同气象要素的均方根误差随时间变化曲线。从图 4可以看出,在初始时刻,由于使用了同样的初始场,TP_BIG和TP_SMALL水平风分量、 温度和高度场的均方根误差都相同; 模式的预报误差随预报时效增加而增大。但是,TP_SMALL的误差增长速度小于TP_BIG; 在积分24 h以后,TP_SMALL和TP_BIG的预报误差的差别明显增大: 水平风分量误差的差别达到了1 m·s-1,温度误差的差别达1 K。表明在给定模式和初始场的条件下,若区域模拟覆盖范围包括高原地区,会局限其下游的预报效果。
|
图 4 TP_BIG和TP_SMALL试验的均方根误差随时间变化曲线 (a)高度场,(b)温度场,(c)纬向风分量,(d)经向风分量 Figure 4 The time change curve of RMSE of WRF forecasts over the “TP” region.(a)height field, (b)temperature field,(c)the zonal wind,(d)meridional wind |
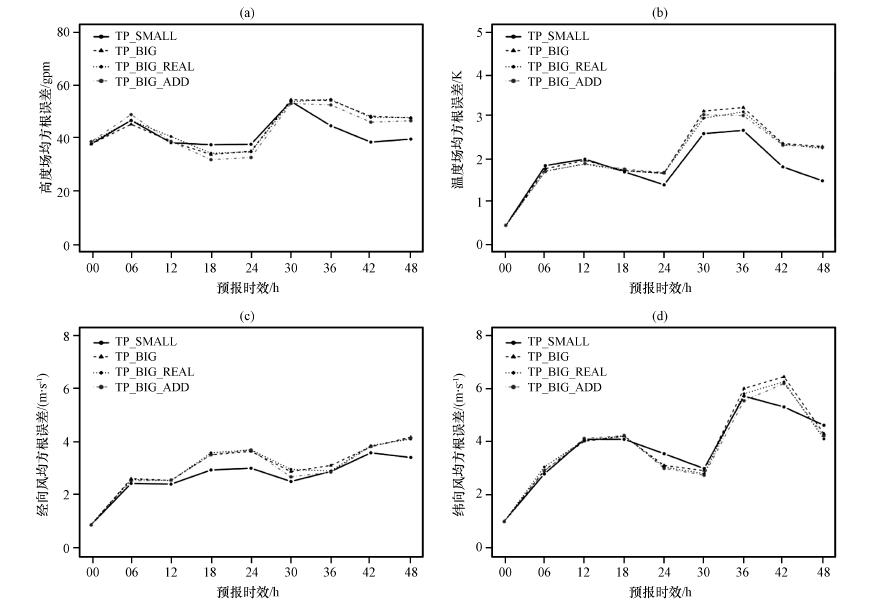
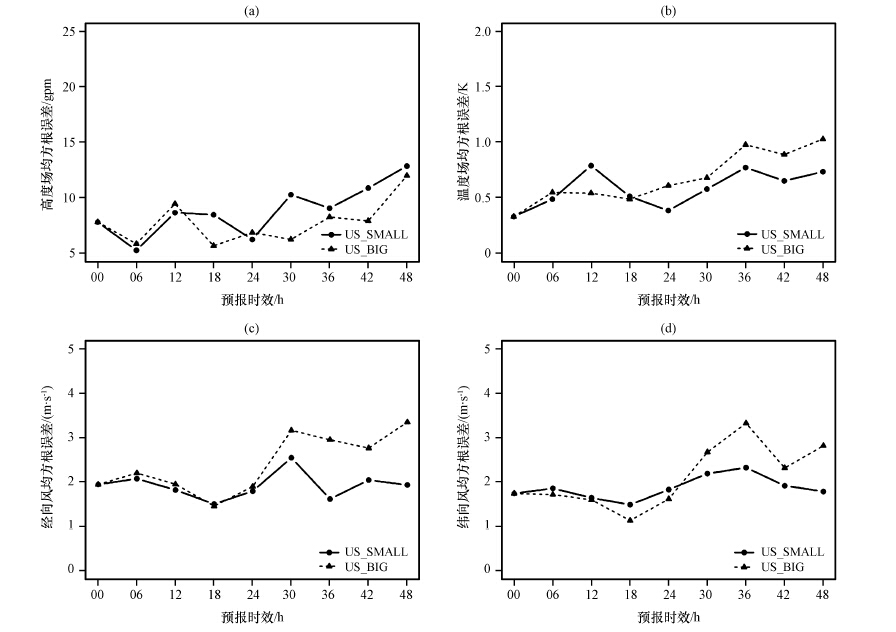
图 5给出了US_BIG和US_SMALL在“落基山脉”下游的均方根误差随时间变化曲线。从图 5中可以看出,对比图 4,落基山脉试验(US_BIG和US_SMALL)的预报误差增长速度较青藏高原试验(TP_BIG和TP_SMALL)慢; US_BIG和US_SMALL区域的误差也有所不同,不过这个差距较TP_BIG和TP_SMALL之间的差距小。简而言之,落基山脉对其下游地区的影响较高原小。
|
图 5 US_BIG和US_SMALL试验的均方根误差随时间变化曲线 (a)高度场,(b)温度场,(c)纬向风分量,(d)经向风分量 Figure 5 The time change curve of RMSE of WRF forecasts over the “US” region.(a)height field, (b)temperature field,(c)the zonal wind,(d)meridional wind |
区域个例试验结果表明: 模式在大地形地区的不确定性会增大其下游地区的预报误差。而这一现象在高原地区十分显著,若模拟区域不包含高原地区,则可以避免高原地区的模式误差对其下游预报的影响。
4 观测系统模拟试验在数值预报中,一般通过观测系统模拟试验来估算新的观测资料对数值预报的影响。本文通过一组观测系统模拟试验OSSE(Observation System Simulation Experiment),估算高原增加的观测对其下游地区预报的影响。尝试通过减少高原初值不确定性,提高其下游地区的预报技巧。
4.1 观测系统模拟试验设置OSSE通常包含3个部分(Prive et al,2013): 替代“真实”大气的“自然”场(Nature run); 由“自然”场生成的人造观测; 用于模拟的资料同化和数值预报系统。能够表征真实大气信息的“自然”场一般通过一段时间的,自由(free)的数值预报提供,而本文的研究中直接使用GFS分析场作为“自然”场,也被称为快捷OSSE试验。
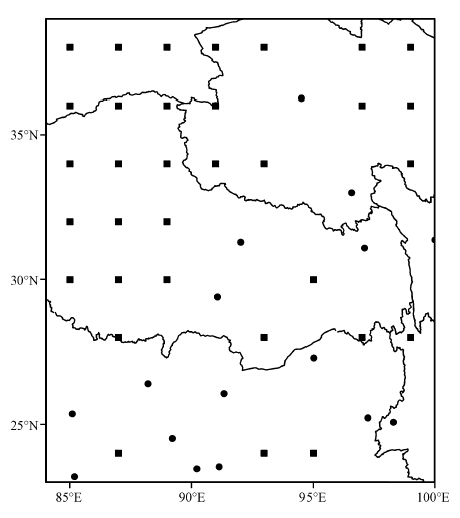
为了预估观测资料对数值预报的影响,OSSE中通常使用“自然”场来生成人造的观测资料。本文中参与OSSE试验的观测资料包含19个常规探空站观测资料和33个“人造”的加密探空资料。图 6为观测系统模拟试验中的观测站点分布。从图 6中可以看出,常规探空站点在高原西部较为稀疏。因此在OSSE试验中,需要在高原西部地区增加“人造”加密探空,以增加高原地区探空观测的密度,进而分析高原地区初值不确定性对下游预报的影响。具体而言,“人造”加密探空站点位置的选取过程如下:先选定一个较为合理的探空影响半径(本文选取的影响半径约为110 km); 然后在高原地区(85°E100°E,24°N39°N)按照影响半径均匀分布“人造”加密探空站点; 计算所有“人造”加密探空站点和常规探空观测站点之间的距离,剔除最小距离<2倍影响半径的“人造”加密探空站点。本文选用的“人造”加密探空站点(共计33个)。人造探空资料和常规探空资料类似,包含温度、 压强、 高度、 风向和风速这些气象要素。具体的生成步骤: 首先通过“自然”场水平和垂直插值到“观测站点”生成“完美”的人造观测; 由于在实际观测中,观测资料包含随机误差、 仪器误差和代表性误差(Errico et al,2013),为了使“人造”观测更加接近实际观测,需要在“完美”的人造观测资料上增加随机误差。随机误差生成方式为以该要素在GSI同化应用中的观测误差作为标准差,使用正态分布函数,生成一组均值为零的随机数,叠加到“完美”观测中,从而得到“人造”探空观测。
|
图 6 观测系统模拟试验中的观测站点分布 Figure 6 The distribution of observing station location of OSSE |
在OSSE试验中用于验证观测资料的预报系统,应该与生成“自然”场的模式不同,以此来避免双子效应(Twin Problems)(Arnold and Dey,1986)。本文OSSE试验的预报系统为ARW-WRF3.4.1,同化系统为GSI(Gridpoint Statistical Interpolation),版本为3.1。
OSSE试验包含两个: TP_BIG_REAL和TP_BIG_ADD。其模REAL式配置和TP_BIG相同。区别在于,TP_BIG_REAL中的初始场为GSI同化后的分析场,参与同化的观测资料为19个实况探空; 而TP_BIG_ADD中的初始场中同化了19个实况探空外还同化了33个“人造”观测资料。具体的模拟试验设置见表 4。
| 表 4 观测系统模拟试验设置 Table 4 The configuration of the OSSE |
同3.1一样,验证区域为TP_SMALL试验覆盖区域,使用METv4.0计算500 hPa高度、 温度和水平风分量的均方根误差。
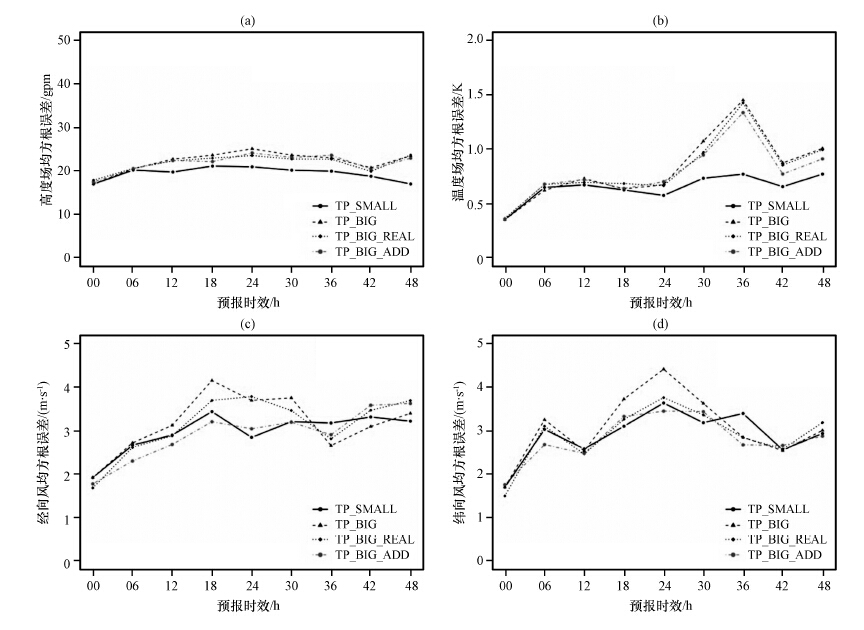
图 7给出了OSSE预报和“自然”场各个变量的均方根误差随时间变化曲线。由图 7可知,在同化了观测资料后,高原下游地区的预报更加接近“真实”大气,特别是水平风分量和高度的误差有明显的减少; TP_BIG_ADD的误差减少最多,因为其同化了实况探空和“人造”探空资料; 图中还给出了3.2中未同化资料的TP_BIG和TP_SMALL的误差变化,虽然TP_SMALL没有同化观测资料,但是其模拟区域未包含高原地区,因而误差最小; 在同化完高原地区的观测资料后,TP_BIG_ADD和TP_BIG_REAL在高原下游地区的误差更加接近TP_SMALL,甚至其水平风场的均方根误差会小于TP_SMALL的误差。图 8和图 9分别为200 hPa和850 hPa各个变量的均方根误差随时间变化曲线。和500 hPa各个变量的均方根误差变化类似,TP_SMALL的误差较其他试验小。在200 hPa,同化完高原地区的观测资料后,TP_BIG_ADD和TP_BIG_REAL在高原下游地区的高度场和温度场误差(图 8a、8b)更加接近TP_SMALL,不过纬向和经向风场(图 8c、8d)的误差反而有所增加。不过在850 hPa,同化完高原地区的观测资料后,TP_BIG_ADD和TP_BIG_REAL在高原下游地区的各个变量(图 9a~d)的误差更加接近TP_SMALL,特别是同化了“人造”加密观测的TP_BIG_ADD试验,误差减少更多。这说明高原地区初值不确定性越小,对其下游的预报影响越少。在实际业务运行中,可以考虑通过大尺度的全球模式预报生成高原上空的“人造”观测资料,作为高原初始场的补充,以改进其下游地区预报。
|
图 7 不同试验的预报误差随时间变化曲线 (a)500 hPa高度场,(b)500 hPa温度场,(c)500 hPa纬向风分量,(d)500 hPa经向风分量 Figure 7 The time change curve of RMSE of WRF forecasts on 500 hPa over the “TP” region.(a)height field, (b)temperature field,(c)the zonal wind,(d)meridional wind |
通过一系列数值试验,探讨数值预报在高原地区的不确定性对其下游地区预报的影响。得到以下主要结论:
(1) 通过利用NCEP的全球预报,比较分析在高原地区及其下游不同地区的预报和分析场,发现积分初始阶段(24 h)高原地区的预报误差最大,其下游不同地区的预报误差自上游向下游(或自西向东)呈阶梯式减小,最远离高原的太平洋中部地区的预报误差最小; 紧邻高原下游地区的预报误差增长率明显大于其他地区。这表明数值预报在高原地区具有较大的不确定性,这种不确定性会制约高原下游地区的预报。
(2) 在同一全球模式提供的初、 边条件下,通过比较分析包含大地形(中国高原和美国落基山)及其下游地区的模拟试验与仅包含大地形下游地区的模拟试验结果表明,前者在大地形下游地区的预报误差明显大于后者; 在积分48 h时,两者误差的差异进一步增大。仅包含大地形下游地区的模拟试验,相当于避免了上游大地形地区的模式不确定性引起的预报误差增长对下游地区的影响。
(3) OSSE试验结果表明,同化高原地区额外的“人造”观测资料,可减少数值预报在高原地区的初值不确定性,进而减小高原本区以及下游地区预报误差。由于当前高原地区观测较为匮乏,在实际数值预报应用中,可考虑使用高质量的分析场或预报场生成“人造”观测资料,经过同化应用以减少高原地区的初值不确定性,进而提高高原及其下游地区预报。
值得指出,本文的快捷OSSE系统还不够严格: 应使用一个独立,自由运行的“自然”场; 而“人造”观测的站点位置确定较为简单,可以使用目标观测技术以确定更加利于青藏高原下游地区预报的“敏感”站点。
| Arnold C J, Dey C. 1986. Observing-system simulation experiments:past, present, and future[J]. Bull Amer Meteor Soc, 67 : 687–695. DOI:10.1175/1520-0477(1986)067<0687:OSSEPP>2.0.CO;2 | |
| Chen Lianshou, Luo Zhexian. 2003. A preliminary study of the dynamicsof eastward shifting cyclonic vortices[J]. Adv Atmos Sci, 20 (3): 323–332. DOI:10.1007/BF02690790 | |
| Danforth C M, Eugenia K, Takemasa M. 2007. Estimating and correcting global weather model error[J]. Mon Wea Rev, 135 (2): 281–299. DOI:10.1175/MWR3289.1 | |
| Davies H C, Marco D. 2013. Diagnosis and dynamics of forecast error growth[J]. Mon Wea Rev, 141 (7): 2483–2501. DOI:10.1175/MWR-D-12-00242.1 | |
| Errico R M, Yang R, Prive N, et al. 2013. Development and validation of observing-system simulation experiments at NASA's Global Modeling and Assimilation Office[J]. Q J Roy Meteor Soc, 139 (674): 1162–1178. DOI:10.1002/qj.v139.674 | |
| Langland R H, Melvyn A S, Ronald G. 2002. Initial condition sensitivity and error growth in forecasts of the 25 January 2000 east coast snowstorm[J]. Mon Wea Rev, 130 (4): 957–974. DOI:10.1175/1520-0493(2002)130<0957:ICSAEG>2.0.CO;2 | |
| MaYaoming, Kang Shichang, Zhu Liping, et al. 2008. Roof of the world:Tibetan observation and research platform[J]. Bull Amer Meteor Soc, 89 (10): 1487–1492. DOI:10.1175/2008BAMS2545.1 | |
| Massimo B, Sam B S. 2004. The role of the Himalayas and the Tibetan Plateau within the Asian monsoon system[J]. Bull Amer Meteor Soc, 85 (7): 1001–1004. DOI:10.1175/BAMS-85-7-1001 | |
| Prive N C, Xie Y, Woollen J S, et al. 2013. Evaluation of the earth systems research laboratory's global observing system simulation experiment system[J]. Tellus A, 65 : 19011. | |
| Qie Xiushu, Xueke Wu, Tie Yuan, et al. 2014. Comprehensive pattern of deep convective systems over the Tibetan Plateau-south Asian monsoon region based on TRMM Data[J]. J Climate, 27 (17): 6612–6626. DOI:10.1175/JCLI-D-14-00076.1 | |
| Szunyogh I, Toth Z, Zimin A, et al. 2002. On the propagation of the effect of targeted observations:The 2000 Winter Storm Reconnaissance Program[J]. Mon Wea Rev, 130 : 1144–1165. DOI:10.1175/1520-0493(2002)130<1144:POTEOT>2.0.CO;2 | |
| Xu Xiangde, Qiuju Miao, Jizhi Wang, et al. 2003. The water transportmodel at the regional boundary during the meiyu period[J]. AdvAtmos Sci, 20 (3): 333–342. | |
| Xu Xiangde, Zhang Renhe, Toshio K, et al. 2008. A new integrated observational system overthe Tibetan Plateau[J]. Bull Amer Meteor Soc, 89 (10): 1492–1496. DOI:10.1175/2008BAMS2557.1 | |
| Zhang Guangzhi, Xu Xiangde, Wang Jizhi. 2003. A dynamic study of Ekman characteristics by using 1998 SCSMEX and TIPEX boundary layer data[J]. Adv Atmos Sci, 20 (3): 349–356. DOI:10.1007/BF02690793 | |
| 何钰, 李国平. 2013. 青藏高原大地形对华南持续性暴雨影响的数值试验[J]. 大气科学 , 37 (4): 933–944. He Yu, Li Guoping. 2013. Numerical experiments on influence of Tibetan Plateau on persistent heavy rain in South China[J]. Chinese J Atmos Sci, 37 (4): 933–944. | |
| 李川, 陈静, 何光碧. 2006. 青藏高原东侧陡峭地形对一次强降水天气过程的影响[J]. 高原气象 , 37 (4): 442–450. Li Chuan, Chen Jing, He Guangbi. 2006. Impact of the steep terrain of eastern Qinghai-Xizang Plateau on the genesis and development of extreme heavy rainfall event[J]. Plateau Meteor, 37 (4): 442–450. | |
| 李跃清. 2011. 第三次青藏高原大气科学试验的观测基础[J]. 高原山地气象研究 , 27 (3): 77–82. Li Yueqing. 2011. The observational basis of the 3rdTibetan Plateau atmospheric scientific experiment[J]. Plateau and Mountain Meteor Res, 27 (3): 77–82. | |
| 梁玲, 李跃清, 胡豪然, 等. 2013. 青藏高原夏季感热异常与川渝地区降水关系的数值模拟[J]. 高原气象 , 32 (6): 1538–1545. DOI:10.7522/j.issn.1000-0534.2013.00028 Liang Ling, Li Yueqing, Hu Haoran, et al. 2013. Numerical study of influence of sensible heat anomalies in summer over Qinghai-Xizang Plateau on rainfall in Sichuan-Chongqing Regions[J]. Plateau Meteor, 32 (6): 1538–1545. DOI:10.7522/j.issn.1000-0534.2013.00028 | |
| 刘式适, 柏晶瑜, 徐祥德, 等. 2000. 青藏高原大地形的动力?热力作用与低频振荡[J]. 应用气象学报 , 11 (3): 312–321. Liu Shikuo, Bai Jingyu, Xu Xiangde, et al. 2000. Dynamic and thermodynamic effects of the Tibetan Plateau and the low-frequency fluctuation[J]. J Appl Meteor Sci, 11 (3): 312–321. | |
| 田红瑛, 田文寿, 雒佳丽, 等. 2014. 青藏高原地区上对流层-下平流层区域水汽分布和变化特征[J]. 高原气象 , 33 (1): 1–13. DOI:10.7522/j.issn.1000-0534.2013.00074 Tian Hongying, Tian Wenshou, Ge Jiali, et al. 2014. Characteristics of water vapor distribution and variation in upper troposphere and lower stratosphere over Qinghai-Xizang Plateau[J]. Plateau Meteor, 33 (1): 1–13. DOI:10.7522/j.issn.1000-0534.2013.00074 | |
| 吴国雄, 刘屹岷, 刘新, 等. 2005. 青藏高原加热如何影响亚洲夏季的气候格局[J]. 大气科学 , 29 (1): 47–56. Wu Guoxiong, Liu Yimin, Liu Xin, et al. 2005. How the Heating over the Tibetan Plateau Affects the Asian Climate in Summer[J]. Chinese J Atmos Sci, 29 (1): 47–56. | |
| 徐祥德, 陈联寿. 2006. 青藏高原大气科学试验研究进展[J]. 应用气象学报 , 17 (6): 756–772. Xu Xiangde, Chen Lianshou. 2006. Advances of the study on Tibetan Plateau experiment of atmospheric Sciences[J]. J Appl Meteor Sci, 17 (6): 756–772. | |
| 郁淑华, 高文良, 彭骏. 2013. 近13年青藏高原切变线活动及其对中国降水影响的若干统计[J]. 高原气象 , 32 (6): 1527–1537. DOI:10.7522/j.issn.1000-0534.2012.00149 Yu Shuhua, Gao Wenliang, Peng Jun. 2013. Statistical analysis of shearline activity in QXP and its influence on rainfall in China in recent 13 years[J]. Plateau Meteor., 32 (6): 1527–1537. DOI:10.7522/j.issn.1000-0534.2012.00149 | |
| 周玉淑, 邓涤菲. 2012. 等σ面相当重力位势分析方法及其对高原低涡个例的检验应用[J]. 大气科学 , 36 (1): 47–62. Zhou Yushu, Deng Difei. 2012. 2012:Analysis method of equivalent isobaric geopotential on σ coordinate and its application to a vortex in the Tibetan Plateau[J]. Chinese J Atmos Sci, 36 (1): 47–62. | |
| 卓嘎, 徐祥德, 陈联寿. 2002. 青藏高原边界层高度特征对大气环流动力学效应的数值试验[J]. 应用气象学报 , 13 (2): 163–169. Zhuo Ga, Xu Xiangde, Chen Lianshou. 2002. Dynamical effect of boundary layer characteristics of Tibetan Plateau on general circulation[J]. J Appl Meteor Sci, 13 (2): 163–169. |
2. Chinese Academy of Meteorological Science, Beijing 100091, China;
3. National Meteorological Centre, Beijing 100091, China;
4. Institute of Urban Meteorology, Beijing 100142, China
 2016, Vol. 35
2016, Vol. 35