2. 南京信息工程大学中国气象局气溶胶-云-降水重点开放实验室, 南京 210044;
3. 成都信息工程大学大气科学学院, 成都 610025
云在天气和气候中起着重要的作用,它是地气辐射能量平衡的重要因子,也是水循环中的重要角色,云和降水过程释放的潜热是各种尺度天气的重要能量来源(Browning et al,1993;Rosenfeld et al,2008)。毫米波云雷达增益高、波长短,可以有效穿透云层获取云内部信息,是研究云宏微观特征和云-降水演变等的有力工具(黄毅梅和周毓荃,2012;刘黎平等,2014;吴举秀等,2014)。中国毫米波云雷达的研制起步较晚,2006年,空军第七研究所与安徽四创电子有限公司联合研制出了8. 6 mm的Ka波段云雷达;2007年,中国气象科学研究院研制出了第一部具有偏振功能的Ka波段云雷达;2013年,安徽四创电子有限公司与南京信息工程大学联合研制了一部3. 2 mm的W波段云雷达,同年中国气象科学研究院与航天科工集团第二十三研究所联合研制出了一部采用固态发射机的Ka波段偏振云雷达(王振会等,2001;程周杰等,2014;张一平等,2014;徐学义等,2014;Wu et al,2014)。
云雷达能够探测到云中不同尺寸的云粒子,这些粒子具备不同的下落速度,雷达返回信号经过快速傅里叶变换后就可以得到不同多普勒速度下的功率分布,即功率谱密度,习惯上也称为多普勒速度谱或功率谱,功率谱中包含了气象目标的散射强度及速度信息,回波功率在不同多普勒速度上的分配对研究大气的运动状态和粒子的滴谱分布等都很关键。近年来国内外学者研究认为,云雷达灵敏度足够探测到云内较微小的云粒子并反映在功率谱中,当云粒子尺度较小时(直径在0 ~ 20 μm),它们自身的下落末速度相对于云内大气的垂直运动速度几乎可以忽略,因此可将这些气流化的小粒子做为示踪物,反演出大气的垂直运动速度,Shupe et al(2008)将这种方法称为小粒子示踪法,该方法基于实测数据,它比传统基于较多假设条件的W0-Z法更为可靠,且对不同云类具有更好的适应性(Gossard et al,1997;Babb,1999;张培昌等,2000;Kollias et al,2001;彭亮等,2012;刘黎平等,2014)。云雷达的功率谱由雷达噪声和云信号组成,云信号谱线的回波功率必需经过定标,而定标时噪声电平是关键。对于噪声电平的计算方法,在早期的天气雷达中是通过设定一个固定值或谱峰下的某固定值(Battan,1964;Donaldson et al,1967,1972;Sekhon and Srivastava,1971),但由于雷达接收到的功率谱并不是固定不变的,在不同天气背景下差异较大,因此该方法效果不令人满意。随后,Peter et al(1975)基于雷达噪声在统计意义上是高斯白噪声的特性,提出了客观噪声电平计算法,算法从谱峰开始不断下降并检测,直至功率谱中气象信号和噪声被正确分离,该方法自提出后就被用于天气雷达中,而近年来也有很多学者将该方法用于确定云雷达的噪声电平(Gossard,1997;Babb,1999;Shupe et al,2008;Luke and Kollias,2013)。在风廓线雷达功率谱研究中,Monique et al(1997)提出一种分段的噪声电平计算法,该方法假设雷达噪声服从自由度为2N/k的中心x2分布,将功率谱分成k段,统计k段各自的平均值,将最小的平均值作为噪声电平,该方法较多被用于风廓线雷达的功率谱中(胡明宝,2012;刘俊等,2015)。王莎等(2012)通过统计风廓线雷达最大速度附近的功率值,将平均值作为噪声电平,该方法假设功率谱中最大速度附近只有噪声而不含有气象信号,与之类似,刘黎平等(2014)认为在云雷达的功率谱中速度> 8 m·s-1对应的基本都为雷达噪声,对该速度位置的功率取平均值作为噪声电平。计算出噪声电平之后,可以从功率谱中识别出云信号,通过信噪比和雷达系统噪声对云信号的回波功率进行定标,并可通过局部积分法计算得到反射率因子、径向速度和谱宽等物理量。
云内大气垂直运动在云的形成、发展和维持过程中扮演了重要角色,利用Ka波段云雷达功率谱对其进行反演具有重要意义,而噪声电平的计算是雷达返回功率定标和反演的重要前提。文章首先提出了一种云雷达功率谱的模拟方法,利用模拟数据定量评估了目前三种主流噪声电平计算方法的准确性,利用评估结果对云信号回波功率进行定标。基于之上,利用小粒子示踪法反演了广东阳江对流云和层状云内的大气垂直运动速度,并提出了假定数浓度和直径下的谱线回波强度临界阈值对反演结果的可靠性进行了定量检验。
2 Ka波段云雷达及其功率谱资料简介2013年中国气象科学研究院与中国航天科工集团第二十三研究所联合研制了一部Ka波段毫米波云雷达,该雷达工作频率为35 GHz,波长为8. 6 mm,最大的特点是采用固态发射机体制和脉冲压缩处理等技术,同时具备双极化功能。在野外观测时,天线垂直指向天顶扫描,距离分辨率高达30 m,时间分辨率高达8. 8 s,即能够在8. 8 s内获取地面至高空的一组廓线资料,资料包含了510个距离库的反射率因子、径向速度、谱宽、退偏振比和功率谱,该雷达的部分雷达参数和性能指标如表 1所示。雷达每个距离库包含一个功率谱数据,功率谱由快速傅里叶变换(FFT)处理后得到,谱点数为256点,对应多普勒速度范围为-9. 27 ~ 9. 27 m·s-1,速度分辨率为0. 0724 m·s-1。
| 表 1 Ka波段云雷达系统的部分参数和性能指标 Table 1 Portion of system parameters and indexes of Ka-band cloud radar |
噪声电平指的是功率谱中所有雷达噪声的平均功率,噪声电平的大小直接影响对雷达返回信号功率的定标和云信号范围的确定。目前,主流的噪声电平计算方法包含:分段噪声电平计算法、最大速度噪声电平计算法和客观噪声电平计算法(本文分别简称为:分段法、最大速度法和客观法)。分段法的原理为:假设雷达功率谱的噪声服从自由度为2 N/k的中心x2分布,即将功率谱分为k段,分别统计出k段功率谱的平均值,取最小的平均值作为噪声电平。最大速度法的原理为:假设雷达功率谱中最大多普勒速度位置处没有气象回波,仅存在着雷达噪声,因此可将最大速度附近的功率值作为噪声电平。客观法的原理为:假设雷达功率谱的噪声是高斯白噪声,则它满足高斯白噪声的两个统计特性,一是统计上噪声的幅度在频带范围内满足均匀分布,二是噪声的瞬间幅度的概率分布满足高斯分布。当功率谱中存在雷达噪声和气象信号时,气象信号功率较高,因此客观法从高功率开始逐渐将功率谱中的气象信号抽离,直至只剩下雷达噪声,计算过程中按抽离后的序列方差是否满足高斯白噪声的方差性质为准则进行判断。客观法可以有效实现功率谱中的气象信号和雷达噪声的自动分离,但也有学者研究发现,该方法存在阈值选取不明确和执行效率较低的缺点(Hildebrand and Sekhon,1974;王莎等,2012);一个原因是气象信号谱峰的功率与雷达噪声的功率数量级差距较大时,若按某阈值从谱峰下降并判断,则计算的次数较多,另一个原因是由于功率谱的谱点有限,雷达噪声组成的序列方差有时难以满足预设的判断条件;针对这两个问题本文对客观法的计算方式进行了调整,具体的计算方法和步骤如下:
(1) 假设功率谱序列为Si(i=1,2,…,M),对其进行由大到小的排序得到序列Sti(i=1,2,…,M),M为功率谱的点数。
(2) 依次将Sti序列中每个点预设为气象信号和噪声的功率分界值,大于该分界值的被认为是气象信号,而小于该分界值的被认为是噪声。将每个分界值分离出的噪声重新组成一组噪声序列,即得到M组噪声序列Sn(n=1,2,…,N)。
(3) 对于每组噪声序列Sn(n=1,2,…,N),假设频率范围为F,第n点的频率为fn,功率为Sn,由于雷达噪声为白噪声,频带范围内的幅度满足均匀分布,则它的方差为
| $~{{\sigma }_{N}}^{2}={{F}^{2}}/12,$ | (1) |
而噪声序列Sn按功率谱的方差定义式求得:
| ${{\sigma }^{2}}=\left( \sum\limits_{n=1}^{N}{{{f}_{n}}^{2}}{{S}_{n}}/\sum\limits_{n=1}^{N}{{{S}_{n}}} \right)-{{\left( \sum\limits_{n=1}^{N}{{{f}_{n}}}Sn/\sum\limits_{n=1}^{N}{{{S}_{n}}} \right)}^{2}},$ | (2) |
定义两者的商为
| $~{{R}_{1}}={{\sigma }^{2}}_{N}/{{\sigma }^{2}},$ | (3) |
根据雷达噪声瞬间幅值的概率密度满足高斯分布,理论上可求得高斯白噪声的方差为
| ${{P}^{2}}={{\left( \sum\limits_{n=1}^{N}{{{S}_{n}}/N} \right)}^{2}},$ | (4) |
而按照随机变量方差的定义式,随机噪声序列Sn的方差为
| $~{{Q}^{2}}=\left( \sum\limits_{n=1}^{N}{{{S}^{2}}_{n}/N} \right)-{{P}^{2}},$ | (5) |
定义P2和Q2的商为
| $~{{R}_{2}}={{P}^{2}}/{{Q}^{2}}\text{ }.$ | (6) |
(4) 通过式(1)~(6)可以得到M个高斯白噪声方差的商R1n和R2n(n=1,2,…,M),理论上,当某分界值能够将气象信号和噪声正确分离时,则满足条件R1 ≈ R2≈1,而实际中,只能用R1 ≈R2≈ 1做为判断条件。对于R1n和R2n,当预设的分界值从谱峰开始往下降时,二者分别表现为下降和上升的过程,当R1n和R2n第一次下降和上升到1时,取两者与1最近的值做为满足R1 ≈R2≈1的条件,此时对应Stn中的预设功率分界值即为信号和噪声的分界值,对该分界值以下的噪声求平均即得到噪声电平。如以上所述,本文在迭代计算前先进行了排序处理,这有效提高了算法的执行效率(功率谱最大到最小值的数量级可差106,假设以101为步长,则需要迭代计算105次,而改进后只需要计算M次,当功率谱点数为256时,即只需要计算256次)。
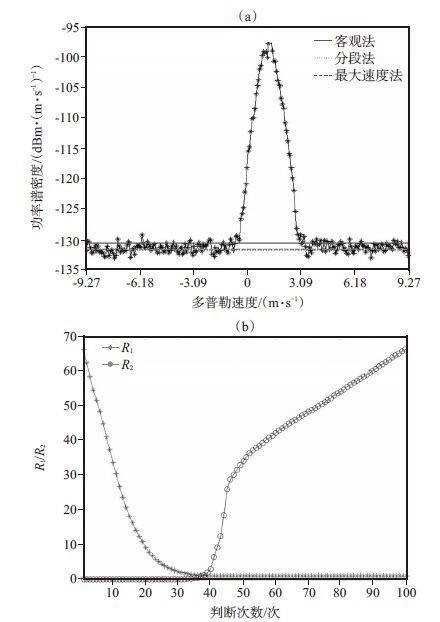
通过云雷达功率谱中三种方法计算的噪声电平效果及R1和R2的变化(图 1)可以看出,分段法计算(图 1a)的噪声电平最低,最大速度法与之相近,而客观法稍微较高。客观法计算(图 1b)过程中R1和R2变化情况,可见,当从谱峰开始按功率大小下降时,R1和R2分别表现为逐渐下降和上升的过程,当运算到第37次时,满足R1 ≈R2≈ 1条件,此时预设的功率即为噪声与信号的分界值,分界值以下组成的噪声序列满足高斯白噪声的性质,噪声的平均功率即为噪声电平。
|
图 1 云雷达功率谱中三种方法计算的噪声电平效果(a)及R1和R2的变化(b) Figure 1 Noise-level calculated effects by three methods (a) and the variation of R1 and R2 (b) |
由于事先很难知道实测功率谱中的噪声电平真值,因此考虑采用模拟的手段,在事先设置噪声电平的情况下模拟出云雷达的功率谱数据,然后利用模拟数据对三种噪声电平计算方法进行定量评估。功率谱是由雷达噪声和云信号组成,二者相互叠加而不相干,因此考虑分别对二者进行模拟(王莎等,2012)。
3.2.1 雷达噪声模拟选取该云雷达2014年6月广东阳江观测资料中随机10000份远距离库的功率谱(远距离库对应位置无云回波,功率谱中全部为雷达噪声),统计了每个距离库功率谱中雷达噪声的平均功率和所有噪声瞬间功率幅值的概率分布,结果表明每个距离库的噪声平均值基本相同,为-131. 4 dBm·(m·s-1)-1左右;而噪声瞬间功率幅值的概率分布(图 2)显示,该噪声瞬间幅值概率分布很好的服从高斯分布,拟合的相关系数达到了99. 95%;因此该云雷达的噪声是高斯白噪声。基于该统计结果,通过构造满足高斯白噪声性质的随机变量来模拟雷达噪声:
| $~{{G}_{n}}\left( {{v}_{i}} \right)=\bar{\mu }+{{F}_{i}}\times \sigma ,$ | (7) |

|
图 2 云雷达10000份功率谱中噪声瞬间幅值的概率分布 Figure 2 Probability distribution of 10000 groups of radar noise instantaneous amplitudes |
式中:vi为多普勒速度;μ为预设的噪声电平;Fi为随机函数;σ为云雷达实测噪声谱线幅值的标准差;σ与Fi乘积代表了雷达噪声在噪声电平上下的随机涨落程度;μ和σ的取值分别为实测功率谱的统计结果。Fi和σ的表达式为
| $~{{F}_{i}}=\sum\limits_{i=0}^{n-1}{\zeta i}-\frac{n}{2},$ | (8) |
| $\sigma =\sqrt{\frac{\sum\limits_{i=1}^{M}{{{\left( {{N}_{i}}-\bar{\mu } \right)}^{2}}}}{M}},$ | (9) |
式中:ζi为(0,1)区间上均匀分布的随机数;n为随机数的个数,根据Lindeberg-levy中心极限定理,当n=12时,随机函数Fi服从标准高斯分布,式(9)中M为统计样本数,Ni为实测的噪声幅值。
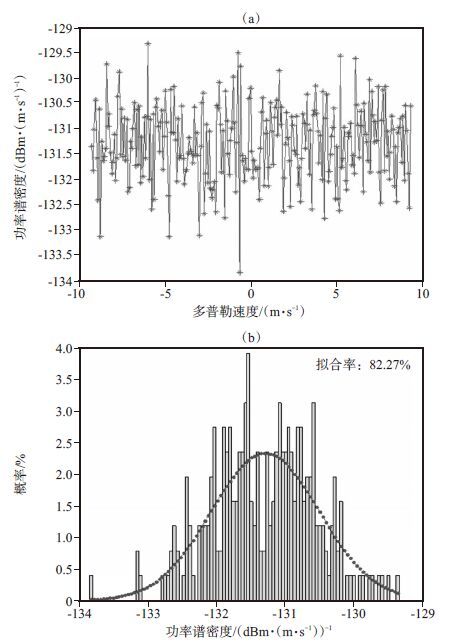
利用该方法模拟的一个云雷达噪声功率谱示例(图 3),功率谱的谱点数、多普勒范围和速度分辨率按实际参数设定为256点、-9. 27 ~ 9. 27 m·s-1和0. 0724 m·s-1,通过噪声的功率谱(图 3a)和噪声瞬间幅值的概率分布(图 3b)可见,该方法能够模拟出满足高斯白噪声性质的雷达噪声。
|
图 3 模拟的云雷达噪声功率谱密度(a)及其瞬间幅值的概率分布(b) Figure 3 Emulational cloud radar noise(a)and the probability distribution of instantaneous amplitudes(b) |
已有研究表明,通常云雨滴信号的功率谱也可近似为高斯分布(Peter et al,1975;Monique,1997;王莎等,2012 ;惠建新等,2012;胡明宝,2012)。因此也考虑根据高斯函数来模拟云信号,模拟时云信号的功率可以利用噪声总功率通过设定一定的信噪比来反映回波的强弱,而对于回波信号的涨落现象,处理方式与噪声类似,我们对雷达实测的云信号功率谱进行高斯拟合,计算拟合的云信号与实测云信号的相对标准偏差,将相对标准偏差与随机函数Fi结合对云信号随机化处理。
| $~{{G}_{s}}\left( {{v}_{i}} \right)={{P}_{r}}\times {{G}_{n}}\left( {{v}_{i}} \right)\times \left( 1+{{F}_{i}}\times \lambda \right),$ | (10) |
| $~{{G}_{n}}\left( {{v}_{i}} \right)=\frac{1}{\sqrt{2\pi {{\sigma }_{v}}}}{{e}^{-\frac{{{\left( {{v}_{i}}-\bar{v} \right)}^{2}}}{2{{\sigma }^{2}}_{v}}}},$ | (11) |
| ${{P}_{r}}={{P}_{n}}\times {{10}^{SNR/10}},$ | (12) |
| $~\lambda =\sqrt{\frac{\sum\limits_{i=1}^{N}{{{\left( \left( Si-f\left( Si \right) \right)/{{S}_{i}} \right)}^{2}}}}{N}},$ | (13) |
式中:Gnvi为模拟的云信号功率谱;vi为多普勒速度;[Gnvi为离散化的高斯函数;v和σv为预设的平均多普勒速度和速度谱宽;Pr为云信号总功率;Pn为噪声总功率;SNR为预设的信噪比;λ是实测云信号功率谱经过高斯拟合后,实测信号值与模拟值的相对标准偏差,它与Fi结合反映了云信号各个谱线的涨落程度,λ取值根据1000份实测云信号功率谱的拟合计算结果为0. 205。
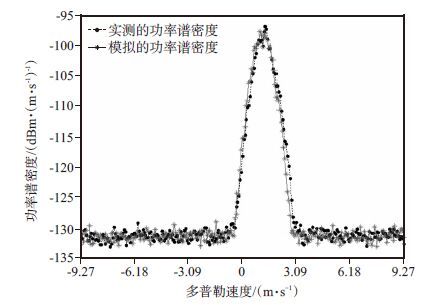
将上述模拟的雷达噪声和云信号叠加后,就可以得到最终模拟的功率谱,图 4给出了一个噪声电平为-131. 5 dBm·(m·s-1)-1,信噪比为20. 18 dB,平均多普勒速度为1. 22 m·s-1,谱宽为0. 39 m·s-1的实测功率谱和模拟功率谱,由图 4可见,模拟的功率谱和实测功率谱是较相近的,无论是谱的形态、谱峰功率、噪声功率和噪声及信号的涨落程度都较为一致,相关系数达到了98. 65%,模拟效果较好。这种在预先设定谱参数情况下的云雷达功率谱模拟方法可以为噪声电平方法的准确性评估提供很好的数据手段。
|
图 4 给定谱参数下的云雷达实测和模拟的功率谱 Figure 4 Observed and simulated cloud radar spectra |
实际中,伴随着云的发展或向降水转化,云回波的强度和运动状态是逐渐在变化的,雷达实测到的功率谱也随着改变,因此在定量评估噪声电平确定方法的准确性时,模拟的功率谱也应该反映出云的强度变化和运动状态变化;云回波强度的变化可以通过设定信噪比来表示,而粒子运动状态可以通过径向速度和谱宽来表示。因此,本文设定了4种云回波状态如表 2所示,从状态1至状态4分别代表了云回波强度逐渐增强,信噪比范围逐渐增大,云内粒子运动从最初的微弱上升运动至云粒子增长到足够大后的下沉运动,同时伴随云粒子增长带来的碰撞和尺度谱的变宽,谱宽也随之增大。针对该四种运动状态下的谱参数,利用模拟的云雷达功率谱对分段法、最大速度法和客观法确定的噪声电平误差进行计算,分段法根据前人的研究结果,段数取为8(Monique,1997;胡明宝,2012),最大速度法取正负Nyquist速度附近的平均值作为噪声电平。
| 表 2 云回波的强度和运动状态 Table 2 Cloud echo intensity and motion state |
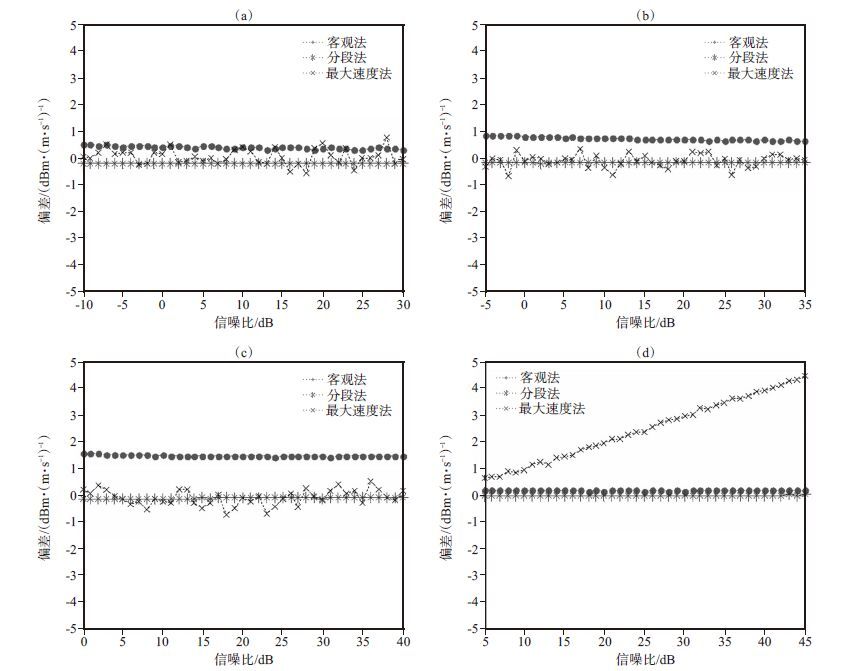
4种状态下,三种噪声电平计算方法的误差如图 5所示。整体上来看,分段法是稍微低估了噪声电平,但低估程度很小,在0. 2 dBm·(m·s-1)-1以下;最大速度法由于Nyquist附近受雷达噪声起伏的影响,误差也随之起伏,误差高低估的程度均在1 dBm·(m·s-1)-1以下,但随着谱宽的增大及粒子运动速度增大,云信号向大速度区分布,此时最大速度附近的谱点不再代表雷达噪声而是云信号,因此最大速度法的误差会较大;对于客观法,4种状态下均高估了噪声电平,高估值在0. 3 ~ 1. 9 dBm·(m·s-1)-1之间,高估的程度是随着谱宽的增大而增大,这是由于功率谱中雷达噪声谱点数的减少会使得客观法将云信号边缘弱的谱点也当成雷达噪声,造成噪声电平偏高。另外当平均速度和谱宽固定时,随着信噪比的逐渐增大,分段法的误差并没有变化,最大速度法的误差是受噪声随机性的影响起伏,而客观法的误差随着信噪比的增大略微有所下降,这说明一定谱宽下客观法的误差会随着回波强度增强而减小。综上分析可知,对于三种噪声电平确定方法,分段法的误差较小,误差基本不随着信噪比的变化而变化,它的适应性和准确性较好。
|
图 5 4种回波状态下分段法、最大速度法和客观法计算的噪声电平误差 (a)~(d)分别为状态1~4 Figure 5 Noise-level calculation bias by using segment method,max-speed method and objective method under four situations. (a)~(d)represent situations 1~4 |
根据第3节的结果选用分段法来计算功率谱中的噪声电平,随后还需自动识别出功率谱中的云信号。通常情况下高于噪声电平的云信号仅为一个包络,但也不排除另外两个特殊情况,一是在云向降水转化的阶段,云信号双峰逐渐演变成双包络,即云滴和雨滴的信号出现了分离;二是当雷达上空出现多层云时,高层降水云形成的雨滴下落至低层非降水云的云体内,此时雷达扫描得到的功率谱中也可能出现双包络的情况。因此,在自动识别功率谱中云信号时要考虑双包络的情况,具体做法如下:(1)确定完噪声电平后,对功率谱中高出噪声电平的连续数据段进行提取,计算出每个连续数据段的功率,并记录下对应的左右端点位置;(2)比较所有段的功率,将功率最大和功率次大对应的数据段初步视为两段气象信号;(3)计算该两个数据段的信噪比,当功率最大数据段的信噪比过小时,认为两个数据段均为雷达噪声,即功率谱中无气象信号,当功率最大数据段的信噪比足够大而功率次大数据段的信噪比又过小时,认为只有前者为气象信号,当功率最大和功率次大数据段的信噪比都足够大时,认为数据段均是气象信号;(4)仅保留被判断为气象信号的数据段左右末端点,并计算出雷达噪声中的最大的噪声功率谱密度值做为云信号和噪声的分界;通过上述步骤即完成对功率谱中云信号的识别,识别出云信号后,利用信噪比和雷达系统噪声分别对云信号每根谱线进行定标。由于功率谱还不能反映不同高度的回波强度情况,因此将功率谱进一步转化为回波强度谱。单根谱线的回波功率Pri实际上是单根功率谱密度谱线S(vi)与多普勒速度间隔Δv的乘积,而谱线的回波功率Pri又可以利用雷达方程转化为回波强度Zi,因此每根谱线扣除掉噪声电平并利用式(14)和(15)将功率谱密度转化成回波强度谱:
| $~{{P}_{ri}}=S\left( {{v}_{i}} \right)\times \Delta v,$ | (14) |
| $\left\{ \begin{matrix} {{Z}_{i}}=\frac{{{P}_{ri}}\times {{R}^{2}}}{C} \\ C=\frac{{{P}_{t}}\times {{G}^{2}}\times \theta \times \phi \times h\times {{\pi }^{3}}\times {{\left| k \right|}^{2}}}{1024\times ln2\times {{\lambda }^{2}}\times L\varepsilon } \\ \end{matrix}, \right.$ | (15) |
式中:C为雷达常数;R为探测距离;Pt为发射功率;G为天线增益;θ和ø为天线水平和垂直波束宽度;h为距离分辨率;|k|2为折射指数;λ为波长;Lε为馈线损耗。
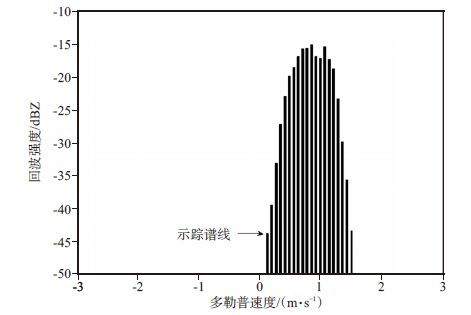
利用小粒子示踪法从云雷达回波强度谱中反演大气垂直运动的依据是:云雷达波长短、灵敏度高对云内小粒子具有较好的探测能力,当云粒子尺度较小(直径0 ~ 20 μm)时,它们的下落速度是远小于大气的垂直运动,因此可将它们在回波强度谱内对应谱线的多普勒速度做为大气的垂直运动速度(Gossard,1997;Babb,1999;Kollias et al,2001;Shupe et al,2008;彭亮等,2012;庄薇等,2013;刘黎平等,2014;吴庆梅等,2014)。如图 6给出了一个广东阳江2014年6月7日17:50(北京时,下同)高度为6 km处的云信号回波强度谱和小粒子示踪法的反演示例。
|
图 6 2014年6月7日17:05阳江6 km高度云信号回波强度谱小粒子示踪法反演结果 Figure 6 Typical case of cloud signal identification and small particle trace method at Yangjiang at 17:50 on 7 June 2014 |
对于小粒子示踪法,反演的准确性与可探测小云粒子的尺度和数浓度有关,若存在20 μm以内的小粒子,则它反演的结果是较准确的,若粒子直径超过20 μm,则反演结果会存在偏差。研究表明,一般情况下,层状云内的云滴数浓度约在102 ~ 103个·cm-3数量级,而积云内的云滴数浓度则相对要小,在102 ~ 103 个·cm-3数量级(盛裴轩等,2003;尹金方,2013),而吴兑等(1988)利用飞机观测资料研究了广东新丰县4 5月上空暖性层积云和浓积云内的云滴谱,结果表明层积云内直径< 20 μm的平均浓度大约在1500个·cm-3,而浓积云内直径小于20 μm的平均浓度大约在1600个·cm-3,出现概率最大的数浓度约在500个·cm-3,平均直径在8 ~ 12 μm之间。由于不同地区不同云类内部的云滴谱差异较大,因此,仅假设在广东阳江地区层状云和积云内直径在20 μm以下的云滴数浓度为500个·cm-3,平均直径为10 μm。从回波强度定义式可算得在这种直径和数浓度下造成的回波强度可达-33 dBZ,故将它作为判断小粒子示踪法可靠性的临界阈值,即若示踪谱线的回波强度大于临界阈值则认为反演结果存在误差,若小于临界阈值则认为反演结果准确可靠。
4.2 个例分析该云雷达具有较高的灵敏度,在5 km处可探测的最小回波强度为-39 dBZ,谱线的回波强度最小为-49 dBZ,理论上具备对20 μm以内云粒子的探测能力。以下选用2014年6月广东阳江探测的对流云和层状云个例分析大气垂直运动速度的反演效果,并利用谱线回波强度临界阈值定量检验结果的可靠性。
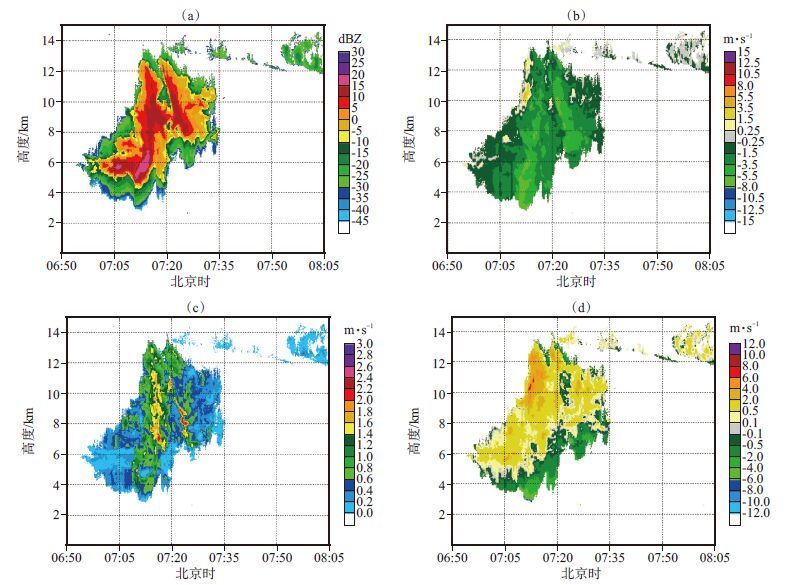
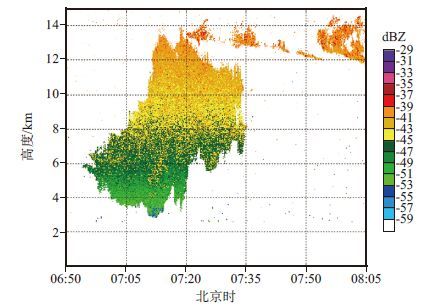
通过2014年6月6日广东阳江观测的一次对流云回波强度、径向速度、谱宽及反演的大气垂直运动速度(图 7)可以看出,该对流云回波(图 7a)最强可达20 dBZ,高度在3 ~ 13 km之间,持续时间在40 min左右;从平均径向速度(图 7b)可见,云内粒子以下沉运动(速度为负)为主,云上部出现了个别正速度区域,说明云上部应该存在上升气流;从谱宽(图 7c)可见,回波较强区域对应着较大谱宽值,在0. 6 ~ 1. 8 m·s-1之间,最大可达2. 2 m·s-1。从反演的云内大气垂直运动速度(图 7d)可见,与从平均径向速度推测的结果一样,反演的对流云中上部分为上升气流,随着高度上升速度有所增大,尤其在07:20之前,云内的9 ~ 13 km位置的上升速度强,最强可达6 m·s-1,在06:55 07:20,云内较强的上升气流使得云内粒子快速增长,因此回波强度增强,谱宽增大,回波可以下伸至3 km;而在07:20 07:35,上升速度有所减弱,回波强度逐渐减弱,谱宽逐渐减小,回波高度在5. 5 km以上;云内的上升气流除了环境场提供之外,云内粒子增长过程中的放热和夹卷效应也会产生贡献,云的底部对应为下沉气流,这是由于云粒子增长到一定尺度后下落速度增长,粒子下沉过程的拖曳及蒸发作用使得大气气流转变为下沉运动。从示踪谱线的回波强度(图 8)可见,所有的示踪谱线回波强度分布在-53 ~ -39 dBZ之间,远小于临界阈值-33 dBZ,说明该对流云内存在可被气流化的示踪小云粒子,该个例所有回波点100%可利用小粒子示踪法较精确反演出大气垂直运动速度。另外,注意到示踪谱线的回波强度从云底到云顶逐渐增加,这与雷达灵敏度随高度下降有关。
|
图 7 2014年6月6日阳江对流云回波强度(a)、径向速度(b)、谱宽(c)及反演的大气垂直运动速度(d) Figure 7 Convective cloud echoes reflectivity (a),mean velocity (b),spectral widthand (c) the retrieved vertical air motion speed (d) at Yangjiang on 6 June 2014 |
|
图 8 2014年6月6日阳江对流云示踪谱线的回波强度 Figure 8 Intensity of traced spectra line of convective cloud at Yangjiang on 6 June 2014 |
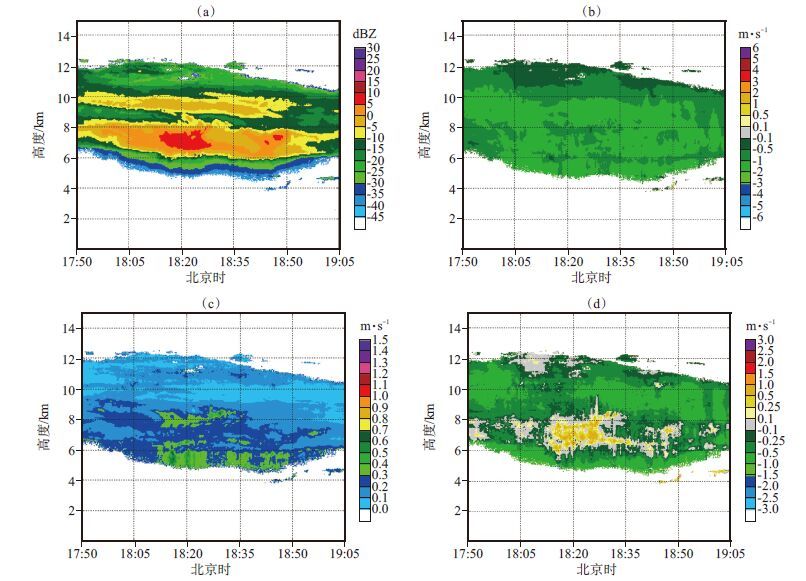
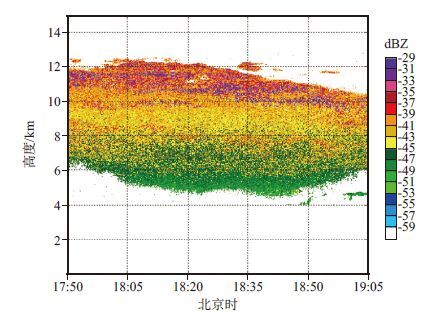
通过2014年6月16日阳江观测的一次层状云回波强度、径向速度、谱宽及反演的大气垂直运动速度(图 9)可以看出,回波高度在5 ~ 12 km,回波强度最强达到10 dBZ,该层状云在雷达上空持续时间在4 h左右。从径向速度显示,云内粒子均为下沉运动,但下落速度较弱,最大只达到-2 m·s-1;从谱宽图可见,云内谱宽很小,最大只达到0. 4 m·s-1,因此云内粒子尺寸较小,云内粒子微物理变化较为缓慢。从反演的云内大气垂直运动来看,云内大部分区域以微弱的下沉气流为主,下沉气流为粒子下落时所带动,下沉速度在-1 m·s-1以内,但在云的6 ~ 8 km之间,云内出现了几个上升气流区域,上升速度也很小,0 ~ 0. 5 m·s-1之间,尤其在18:12 18:35时段,上升气流相对较强,它与强回波区有很好的对应,这说明即使上升气流较弱,它对云粒子增长依然很重要。从示踪谱线的回波强度(图 10)可见,10 km以下,示踪谱线的回波强度在-53 ~ -39 dBZ之间,均小于临界阈值,10 km以上,大部分也在-35 dBZ以下,但有少数谱线的回波强度超过了临界阈值;整体来看,该层状云内有96. 23%回波点满足小粒子示踪法的条件,则反演的大气垂直运动较准确可靠。
|
图 9 2014年6月16日阳江层状云回波强度(a),径向速度(b),谱宽(c)及反演的大气垂直运动速度(d) Figure 9 Stratiform cloud echoes reflectivity (a),mean velocity (b),spectral widthand (c) the retrieved vertical air motion speed (d) at Yangjiang on 16 June 2014 |
|
图 10 2014年6月16日阳江层状云示踪谱线的回波强度 Figure 10 Intensity of traced spectra line of stratiform cloud at Yangjiang on 16 June 2014 |
(1) 利用云雷达的高斯白噪声特征和云信号满足高斯分布特征,结合实测数据统计得到的涨落程度,可以模拟出给定谱参数的功率谱,模拟数据与实测十分相近,可做为功率谱定量研究的有效数据源。
(2) 三种噪声电平计算方法中,最大速度法受噪声起伏的影响,误差在1 dBm·(m·s-1)-1以内,客观法计算结果偏高0. 3 ~ 1. 9 dBm·(m·s-1)-1,分段法最准确,误差在0. 2 dBm·(m·s-1)-1以内;稳定性上,当谱宽和多普勒速度较大时客观法和最大速度法误差达到很大,而分段法受影响较小。
(3) 谱线回波强度临界阈值的检验结果表明,该对流云内所有示踪谱线的回波强度均远小于临界阈值,云内100%距离库为被反演,反演结果可靠;该层状云内,除了少数距离库,大部分示踪谱线的回波强度在临界阈值以下,云内96. 23%距离库可被反演,反演结果可靠;对流云和层状云内示踪谱点的回波强度均随着探测高度升高而增大,这是雷达灵敏度随高度下降的表现。
致谢 本文受到中国气象科学研究院灾害性天气国家重点实验室的葛润生研究员和阮征研究员的悉心指导,在此表示感谢。| Battan L J. 1964. Some observations of vertical velocities and precipitation sizes in a thunderstorm[J]. J Appl Meteor, 3 (4): 415–420. DOI:10.1175/1520-0450(1964)003<0415:SOOVVA>2.0.CO;2 | |
| Babb D M, Verlinde J, Albrecht B A. 1999. Retrieval of cloud microphysical parameters from 94-GHz radar Doppler power spectra[J]. J. Atmos Oceanic Technol, 16 (5): 489–503. DOI:10.1175/1520-0426(1999)016<0489:ROCMPF>2.0.CO;2 | |
| Donaldson Jr R J. 1967. A preliminary report on Doppler radar observation of turbulence in a thunderstorm[R]. Air Force Cambridge Research Laboratories,Environ Res Papers,No. 255,19. | |
| Donaldson R J. 1972. Measurement of wind gradients in convective storms by Doppler radar[C]//Champaign-Urbana:Preprints Fifteenth Radar Meteorology Conference,22-26. | |
| Gossard E E, Snider J B, Clothiaux E E, et al. 1997. The potential of 8-mm radars for remotely sensing cloud drop size distributions[J]. J Atmos Oceanic Technol, 14 (1): 76–87. DOI:10.1175/1520-0426(1997)014<0076:TPOMRF>2.0.CO;2 | |
| Kollias P, Albrecht B A, Lhermitte R, et al. 2001. Radar observations of updrafts,downdrafts,and turbulence in fair-weather cumuli[J]. J Atmos Sci, 58 (13): 1750–1766. DOI:10.1175/1520-0469(2001)058<1750:ROOUDA>2.0.CO;2 | |
| Luke E P, Kollias P. 2013. Separating cloud and drizzle radar moments during precipitation onset using Doppler spectra[J]. J Atmos Oceanic Technol, 30 (8): 1656–1671. DOI:10.1175/JTECH-D-11-00195.1 | |
| Petitdidier M, Sy A, Garrouste A, et al. 1997. Statistical characteristics of the noise power spectral density in UHF and VHF wind profilers[J]. Radio Science, 32 (3): 1229–1247. DOI:10.1029/97RS00250 | |
| Hildebrand P H, Sekhon R S. 1974. Objective determination of the noise level in Doppler spectra[J]. J Appl Meteor, 13 (7): 808–811. DOI:10.1175/1520-0450(1974)013<0808:ODOTNL>2.0.CO;2 | |
| Rosenfeld D, Lohmann U, Raga G B, et al. 2008. Flood or drought:how do aerosols affect precipitation?[J]. Science, 321 (5894): 1309–1313. DOI:10.1126/science.1160606 | |
| Sekhon R S, Srivastava R C. 1971. Doppler radar observations of drop-size distributions in a thunderstorm[J]. J Atmos Sci, 28 (6): 983–994. DOI:10.1175/1520-0469(1971)028<0983:DROODS>2.0.CO;2 | |
| Shupe M D, Kollias P, Poellot M, et al. 2008. On deriving vertical air motions from cloud radar Doppler spectra[J]. J Atmos Oceanic Technol, 25 (4): 547–557. DOI:10.1175/2007JTECHA1007.1 | |
| Browning K A, Betts A, Jonas P R, et al. 1993. The GEWEX cloud system study(GCSS)[J]. Bull Amer Meteor Soc, 74 (3): 387–399. DOI:10.1175/1520-0477(1993)074<0387:TGCSS>2.0.CO;2 | |
| Wu J, Wei M, Hang X, et al. 2014. The first observed cloud echoes and microphysical parameter retrievals by China's 94-GHz cloud radar[J]. J Meteor Res, 28 : 430–443. DOI:10.1007/s13351-014-3083-x | |
| 程周杰, 魏鸣, 朱亚平, 等. 2014. 双偏振天气雷达探测量的伪彩合成[J]. 高原气象 , 33 (5): 1448–1456. DOI:10.7522/j.issn.1000-0534.2013.00088 Cheng Zhoujie, Wei Ming, Zhu Yaping, et al. 2014. Pseudo-color composite for polarimetric radar[J]. Plateau Meteor, 33 (5): 1448–1456. DOI:10.7522/j.issn.1000-0534.2013.00088 | |
| 胡明宝. 2012. 风廓线雷达数据处理与应用研究[D]. 南京:南京信息工程大学. Hu Mingbao. 2012. Reseach on data processing and application of wind profile radar[D]. Nanjing:Nanjing University of Information Science & Technology. | |
| 黄毅梅, 周毓荃. 2012. 95 GHz云雷达对一次冷锋云系结构的观测分析[J]. 高原气象 , 31 (4): 1129–1138. Huang Yimei, Zhou Yuquan. 2012. Analysis on cold front cloud structure from 95 GHz cloud radar data[J]. Plateau Meteor, 31 (4): 1129–1138. | |
| 惠建新, 吴蕾, 高玉春, 等. 2012. 基于极大似然算法的风廓线雷达谱矩估计[J]. 气象科技 , 40 (1): 9–14. Hui Jianxin, Wu Lei, Gao Yuchun, et al. 2012. Study of spectral moments estimations for wind-profiling radar based on maximum likelihood algorithm[J]. Meteor Sci Technol, 40 (1): 9–14. | |
| 刘俊, 黄兴友, 何雨芩, 等. 2015. X波段相控阵气象雷达回波数据的对比分析[J]. 高原气象 , 34 (4): 1167–1176. DOI:10.7522/j.issn.1000-0534.2014.00043 Liu Jun, Huang Xingyou, He Yuqin, et al. 2015. Comparative analysis of X-band phased array antenna weather radar measurements[J]. Plateau Meteor, 34 (4): 1167–1176. DOI:10.7522/j.issn.1000-0534.2014.00043 | |
| 刘黎平, 谢蕾, 崔哲虎. 2014. 毫米波云雷达功率谱密度数据的检验和在弱降水滴谱反演中的应用研究[J]. 大气科学 , 38 (2): 223–236. Liu Liping, Xie Lei, Cui Zhehu. 2014. Examination and application of doppler spectral density data in drop size distribution retrieval in weak precipitation by cloud radar[J]. Chinese J Atmos Sci, 38 (2): 223–236. | |
| 彭亮, 陈洪滨, 李柏. 2012. 3 mm多普勒云雷达测量反演云内空气垂直速度的研究[J]. 大气科学 , 36 (1): 1–10. Peng Liang, Chen Hongbin, Li Bai. 2012. A case study of deriving vertical air velocity from 3 mm cloud radar[J]. Chinese J Atmos Sci, 36 (1): 1–10. | |
| 盛裴轩, 毛节泰, 李建国, 等. 2003. 大气物理学[M]. 北京: 北京大学出版社, 290-307. Sheng Peixuan, Mao Jietai, Li Jianguo, et al. 2003. Atmospheric physics[M]. Beijing: China Meteorological Press , 290-307. | |
| 王莎, 阮征, 葛润生. 2012. 风廓线雷达探测大气返回信号谱的仿真模拟[J]. 应用气象学报 , 23 (1): 20–28. Wang Sha, Ruan Zheng, Ge Runsheng. 2012. Simulation of return signal spectraum of wind profile radar[J]. J. Appl Meteor Sci, 23 (1): 20–28. | |
| 王振会, 纪雷, 黄兴友, 等. 2011. 机载W波段测云雷达回波强度衰减订正仿真研究[J]. 高原气象 , 30 (2): 437–444. Wang Zhenhui, Ji Lei, Huang Xingyou, et al. 2011. Simulation study on the attenuation correction to reflectivityfactor observed with an air-borne W-band cloud radar[J]. Plateau Meteor, 30 (2): 437–444. | |
| 吴兑, 何应昌, 陈桂樵. 1988. 广东新丰江流域4-5月暖云的微物理特征[J]. 热带气象学报 , 4 (4): 341–349. Wu Dui, He Yingchang, Chen Guiqiao. 1988. The microphysical features of warm clouds over the Xingfeng Jiang River valley in Guangdong during Apri to May[J]. J Trop Meteor, 4 (4): 341–349. | |
| 吴举秀, 魏鸣, 周杰. 2014. 94 GHz云雷达回波及测云能力分析[J]. 气象学报 , 72 (2): 402–416. Wu Juxiu, Wei Ming, Zhou Jie. 2014. Echo and capability analysis of 94 GHz cloud radars[J]. Acta Meteor Sinica, 72 (2): 402–416. | |
| 吴庆梅, 杨波, 王国荣. 2014. 北京地区一次回流暴雪过程的锋区特征分析[J]. 高原气象 , 33 (2): 539–547. DOI:10.7522/j.issn.1000-0534.2014.00081 Wang Qingmei, Yang Bo, Wang Guorong. 2014. Analysis of the frontal characteristics of the backflow snowstorm process in Beijing area[J]. Plateau Meteor, 33 (2): 539–547. DOI:10.7522/j.issn.1000-0534.2014.00081 | |
| 徐学义, 赵振东, 梁红新. 2014. 三次非超级单体龙卷风暴多普勒雷达特征对比分析[J]. 高原气象 , 33 (4): 1164–1172. DOI:10.7522/j.issn.1000-0534.2013.00036 Xu Xueyi, Zhao Zhendong, Liang Hongxin. 2014. Comparative analysis on doppler radar echo features of three non-supercell tornadic storms[J]. Plateau Meteor, 33 (4): 1164–1172. DOI:10.7522/j.issn.1000-0534.2013.00036 | |
| 尹金方. 2013. 东亚区域云和降水微物理特征及云微物理方案参数化方案构建[D]. 杭州:浙江大学博士学位论文. Yin Jinfang. 2013.The study on observation and parameterization of cloud-precipitation microphysical properties over East Aisa[D]. Hangzhou:PHD Dissertation of Zhejiang University. http://cn.bing.com/academic/profile?id=62fca557a2083a248feb4e12b8b7ace6&encoded=0&v=paper_preview&mkt=zh-cn | |
| 张培昌, 杜秉玉, 戴铁丕. 2000. 雷达气象学[M]. 北京: 气象出版社, 223-236. Zhang Peichang, Du Bingyu, Dai Tiepi. 2000. Radar Meteorology[M]. Beijing: China Meteorological Press , 223-236. | |
| 张一平, 俞小鼎, 孙景兰, 等. 2014. 一次槽后型大暴雨伴冰雹的形成机制和雷达观测分析[J]. 高原气象 , 33 (4): 1093–1104. DOI:10.7522/j.issn.1000-0534.2012.00200 Zhang Yiping, Yu Xiaoding, Sun Jinglan, et al. 2014. Formation mechanism and analysis of radar observation of a heavy rainstorm accompanied by hail that back of trough[J]. Plateau Meteor, 33 (4): 1093–1104. DOI:10.7522/j.issn.1000-0534.2012.00200 | |
| 庄薇, 刘黎平, 王改利, 等. 2013. 青藏高原复杂地形区雷达估测降水方法研究[J]. 高原气象 , 32 (5): 1224–1235. DOI:10.7522/j.issn.1000-0534.2012.00118 Zhuang Wei, Liu Liping, Wang Gaili, et al. 2013. Radar-derived quantitative precipitation estimation in complex terrain area in Qinghai-Xizang Plateau[J]. Plateau Meteor, 32 (5): 1224–1235. DOI:10.7522/j.issn.1000-0534.2012.00118 |
2. Key Laboratory for Aerosol-Cloud-Precipition of China Meteorological Adiministration, Nanjing University of Information Science and Technology, Nanjing 210044, China;
3. Chengdu University of Information Technology, School of Atmospheric Sciences, Chengdu 610225, China
 2016, Vol. 35
2016, Vol. 35