2. 南京信息工程大学 大气物理学院, 南京 210044
中国是一个对流性天气灾害多发的国家。随着国民经济和社会的快速发展,突发性的灾害性天气对社会经济和人民生活的影响日益加剧,极端天气气候现象事件增多给农业、水资源、能源和国防等安全保障带来极大影响(刘杰等,2012; 翟盘茂和刘静,2012; 温颖等,2015)。天气雷达已经成为突发性强对流天气的重要观测和预警手段之一(张沛源等,2008; 李柏等,2013; 张之贤等,2014),目前我国已经拥有近200部新一代多普勒天气雷达。
新一代天气雷达在一定条件下具有其他观测手段无可比拟的优越性(张一平等,2014; Serafin and Wilson,2000)。但是,地面位置固定的单部天气雷达因其波束为锥形(空间尺度随距离增大而增大)等影响而造成远距离处探测能力降低、探测范围有限、难以探测大尺度天气系统,如台风、梅雨锋等。为此,研究对单部雷达远距离处的低分辨率资料进行“插值”处理(邹海波等,2014),并研究将多部天气雷达联网观测(张蕾等,2011),从而增强防灾减灾能力(杨吉等,2012; 段艺萍等,2014)。联网观测资料处理中,也涉及到“插值”计算(肖艳娇和刘黎平,2006)。插值的常用方法有:(1)最近邻居法(Jorgensen et al,1983);(2)线性内插法(Fulton,1998; Mohr and Vaughn,1979; Miller et al,1986);(3)Cressman权重方法(Weygandt,2002);(4)Barnes方法或指数权重方法(Shapiro et al,2003; Askelson et al,2000)。单个仰角平面内雷达资料网格化的方法主要为最近邻居法和双线性插值法两种(邹海波等,2014)。其中最近邻居法基于网格单元中心和雷达数据距离库中心的距离,因此随着径向距离的增加,相邻两个方位角的距离库的中心离得越远,雷达反射率因子之间的差别就可能越大,从而出现回波插值明显不连续,这种方法虽然耗时最少,但是精确度较低(黄云仙和张英,2008)。线性内插法在雷达数据处理中得到广泛的应用,张培昌(1989)介绍将单站 CAPPI 资料坐标转换成统一的地理经纬度坐标和底图直角坐标,再通过双线性插值法转换成底图直角坐标网格点上。为了得到不同的插值效果,也有把这几种插值算法相结合的,如王庆东等(2002)用垂直投影法和两次双线性(距离和方位)及一次线性值插值(仰角)得到网格点的回波强度,肖艳姣等(2006)采用了径向与方位上最近邻居法和垂直方向上线性内插法相结合(NVI方法)的方法。
但这些插值方法的共同点是,插值点的插值都是居于其附近观测点所取极大值和极小值之间。而在距离雷达较远的区域内可能存在一些强降水中心,没有被雷达观测到,也不可能用插值法插值出来。这就导致在远距离的回波图上缺少可能存在的一些强回波中心,这些强回波中心在进行雷达拼图的时候因显现不出来,而使回波更加平滑,进而影响了在数值模式同化预报、灾害预警中揭示强对流天气的应用。
在目前的业务天气雷达上、适当距离范围内,产生对流性降水的积状云(含浓积云、积雨云等)波动特征明显。而波动特征不明显的区域,可以是分布均匀的层状云弱回波区,也可以是因雷达分辨率过低而被空间平滑的区域,或是因距离过远而难以使用雷达探测积状云波动特征的区域。
本文基于傅里叶谱分析原理,提出一种新的插值方法,该方法在分析雷达回波时通过内插计算来显示适当距离处具有波动特征、产生对流性降水的“积状云”由于波束展宽、分辨率下降导致雷达探测不到的强回波中心,为进一步精确识别强回波中心位置和强度提供参考。
2 理论与算法介绍 2.1 理论简介傅立叶变换是数据信号分析中常用的一种方法,利用频率、幅值和相位来描述时域中的振动波形,进而分析数据的规律和特征,并且在气象上已得到广泛的应用(张红等,2006; 肖现等; 2008)。本研究将雷达观测数据看成时间序列,如: 在给定的雷达观测方向上,假设以Δt=1为采样间隔(即库),到采样点的最大距离处共有460库,则在此方向上获得N= 460个回波强度(张培昌和王振会,2001),记为
| $~{{X}_{1}},{{X}_{2}},\ldots ,{{X}_{N}},$ | (1) |
用序列表示为
| ${{X}_{t}}=\left\{ {{X}_{1}},{{X}_{2}},\ldots ,{{X}_{N}} \right\},$ | (2) |
其基本周期T等于序列的长度,基本周期对应的波称为基波,基波频率为f1=1/N。第i次谐波频率记为i*f1=i/N。按照傅里叶谱分析(黄嘉佑,2000),此序列可表示为
| ${{X}_{t}}={{A}_{0}}+\sum\limits_{i=1}^{p}{{{A}_{i}}cos\left( {{\omega }_{i}}t-{{\varphi }_{i}} \right),}$ | (3) |
其中: A0为序列的算术平均值; Ai为各谐波的振幅; φi为各谐波的相角; ωi=2πfi为谐波频率; p=N/2=230为谐波分量个数,共有230个谐波分量。也可表示为
| ${{X}_{t}}={{A}_{0}}+\sum\limits_{i=1}^{p}{\left[ {{a}_{i}}cos\left( 2\pi it/N \right)+{{b}_{i}}sin\left( 2\pi it/N \right) \right].}$ | (4) |
这里,傅立叶系数
| $\left\{ \begin{matrix} {{a}_{i}}=\frac{2}{N}\sum\limits_{t=1}^{N}{{{X}_{t}}cos\left( 2\pi it/N \right)} \\ {{b}_{i}}=\frac{2}{N}\sum\limits_{t=1}^{N}{{{X}_{t}}sin\left( 2\pi it/N \right)} \\ \end{matrix} \right.,\left( i=1,2,\ldots ,p \right)$ | (5) |
可由傅里叶变换计算得到。由傅立叶系数得到谐波振幅与相位:
| $\left\{ \begin{matrix} {{A}_{i}}=\sqrt{{{a}^{2}}_{i}+{{b}^{2}}_{i}} \\ {{\varphi }_{i}}=arctan\frac{{{b}_{i}}}{{{a}_{i}}} \\ \end{matrix} \right.,\left( i=1,2,\ldots ,p \right)$ | (6) |
由于序列(1)是随距离连续变化的雷达回波强度经离散采样而得到的,故可视为雷达回波强度随距离的变化,所以,把公式(6)计算得到的谐波振幅与相位代入公式(3),求全部谐波分量之和(p=N/2),可以得到任意距离(用t值表示)所对应的Xt,即对于这条径向上的任意距离,都可以给出相应的回波值。实际上,这样进行插值的本质是利用傅里叶谱分析获得产生对流性降水的积状云回波强度时空变化的谱特征并进一步用于观测数据离散点拟合、再进行重采样。
2.2 算法描述记雷达某一仰角PPI图有G个方位角,每个方位角上有H个距离库,因此,一个径向上H个距离所组成的数据称为径向数据(H个数值),同一距离上G个方位所组成的一维数据为切向数据(G个数值),那么一张雷达PPI图含有G组径向数据和H组切向数据。
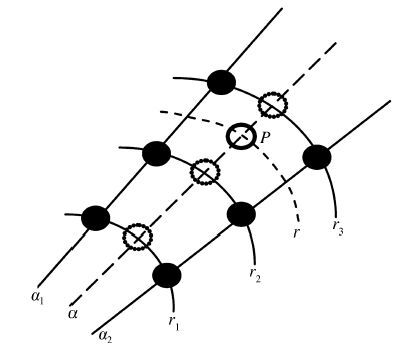
利用上述理论,对PPI形式的二维雷达回波数据的切向数据和径向数据先、后进行一维插值运算,即可在PPI图上得到任意方位和距离库的回波值。根据二维傅里叶变换的性质,切向、径向数据插值的顺序对结果没有影响,采用先切向、再径向的插值顺序。如图 1所示,黑色点为雷达探测到的点,P为插值点,α1、α2为相邻方位角,r1、r2、r3为相邻距离库,α和r是插值点P的方位和距离。
|
图 1 傅里叶插值示意图 Figure 1 An illustration for Fourier interpolation |
具体插值步骤为:
第一步,利用公式(5)和(6)对第1个切向(记为h=1,即距离雷达最近的距离圈)上的G个数据计算傅里叶系数、谐波振幅与相位(在这一步的计算中,令式(5)中的N=G);
第二步,将上一步得到的谐波振幅与相位代入公式(3),并令式(3)中的t=α,则计算出第1个切向上、方位α处的Xt值;
第三步,如此依次取h=2,…,H重复前两步,得到方位角为α时H个切点上的回波值(如图 1中的虚线小圈);
第四步,将第三步得到的H个回波值作为一组径向数据,仿照第一步(但在这一步的计算中,令式(5)中的N=H)利用公式(5)、(6)计算傅里叶系数、谐波振幅与相位;
第五步(仿照第二步)将上一步得到的谐波振幅与相位代入公式(2)并令式(2)中的t等于r,则计算出方位=α且距离=r处的回波值,即P(r,α)。
由于上述计算中r和α 为任意值,故重复上述计算(改变r,重复第五步; 改变α,重复第二至第五步),可得出PPI上雷达探测范围内任意点的回波值。
3 个例实验如前所述,最近邻居法在处理单个仰角平面内雷达资料插值时精确度最低,所以文中用双线性插值法作为参照,对傅里叶插值法进行效果对比。
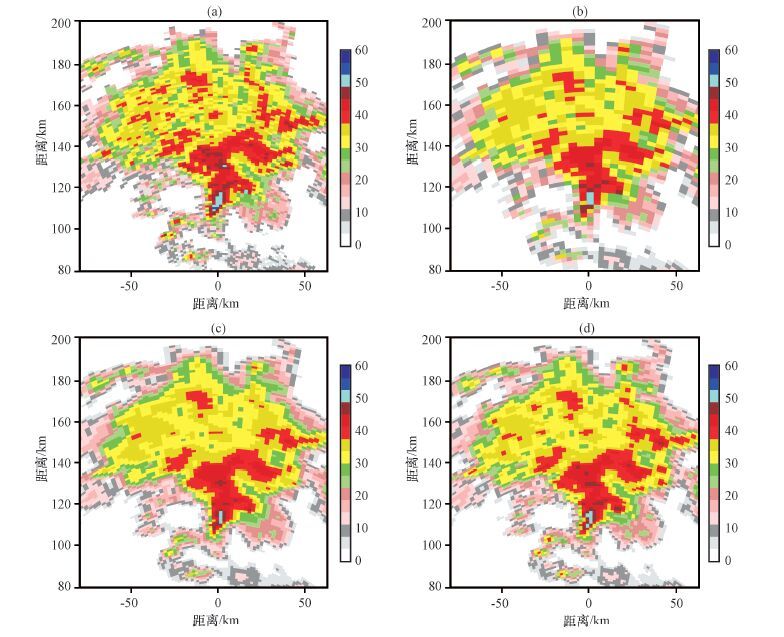
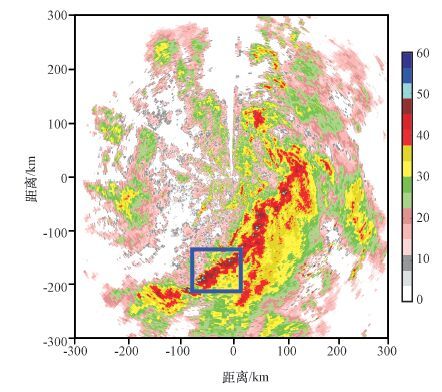
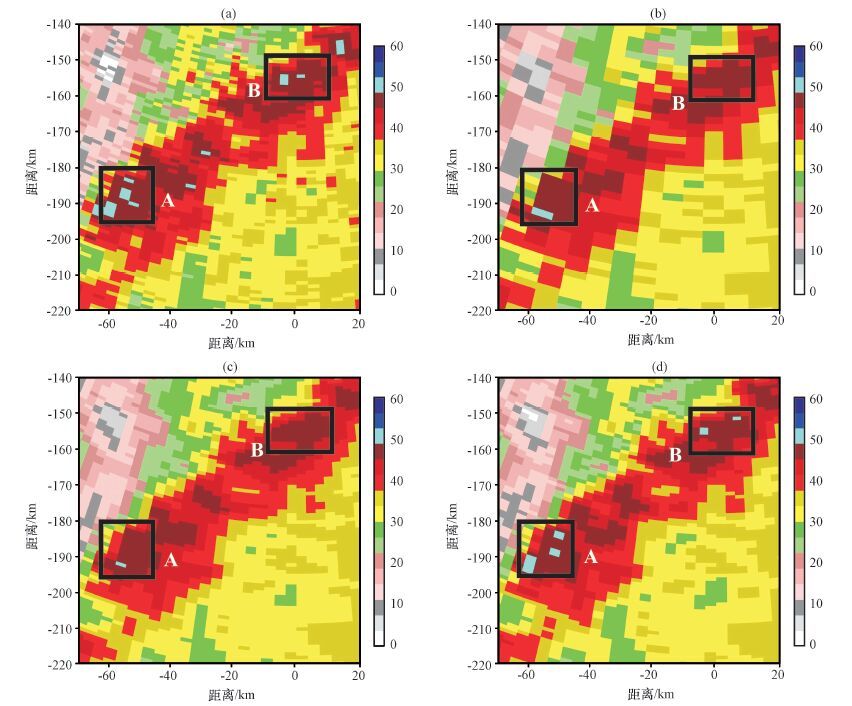
3.1 个例12008年7月29日00:18(北京时,下同),台风“凤凰”在福州南部沿海登陆,此时福州雷达0. 5°仰角的回波PPI图(图 2),中心点为雷达位置。从图 2可看出,在雷达的东南方向有一条范围较大的气旋性带状强回波区,在带状回波上有多个强回波中心。以距离较远的蓝色框内强对流区域为例,放大后如图 3a,分辨率为1°×1 km(1°在距离180 km处相当于3 km),作为真值。为了进行插值效果对比,按照空间权重平均(参照雷达气象学中对雷达反射率因子的定义)将图 3a分辨率降为2°×2 km,如图 3b,假设其为低分辨率雷达探测得到的回波图,对图 3b按照1°×1 km分辨率进行插值(即分辨率复原),用双线性插值和傅里叶插值两种方法,分别得到结果如图 3c和3d。图 3b因分辨率降低而平滑了图 3a中的几处强回波中心,图 3c尽管空间分辨率提高了,但因双线性插值的平滑性质进一步埋没了本来存在的几处强回波中心,而图 3d则因傅里叶插值的优势明显改善了图 3b中的强回波中心显示。图 3d与图 3a更接近。尤其是在图 3黑框选定的区域A中,高分辨率雷达数据(即真值)中有较多强回波区域(蓝点),低分辨率雷达只探测到了一小块强回波。对低分辨率雷达回波进行插值后,双线性插值不仅没有插值出实际应有的回波,而且强回波中心点的范围也变小了; 傅里叶插值后,区域内出现了一些较强的回波,仅其位置与图 3a差一个像素(1 km)。同样的,区域B中,高分辨率雷达探测到了两个强回波中心点,而低分辨率雷达却没有探测到,双线性插值后的结果也没有出现强回波中心点,傅里叶插值使两个强回波中心重现,其位置仅差一个像素。图 3右下角有大片的弱回波区,在这片区域图 3b、3c和3d都比较一致,说明傅里叶插值在处理弱回波区数据时,其效果与双线性插值相差不大。
|
图 2 008年7月29日00:18福州雷达0. 5°仰角的PPI回波分布(单位: dBZ) Figure 2 Radar echo PPI at 0. 5° elevation of Fuzhou radar at 00:18 on 29 July 2008. Unit: dBZ |
|
图 3 个例1的雷达回波效果对比(单位: dBZ) (a)高分辨率雷达回波,(b)低分辨率雷达回波,(c)为图(b)的双线性插值结果,(d)为图(b)的傅里叶插值结果 Figure 3 Comparisonof radar echo for Case one. Unit: dBZ. (a)Higher resolution radar echo,(b)lower resolution radar echo,(c)bilinear interpolation results from(b),(d)Fourier interpolation results from(b) |
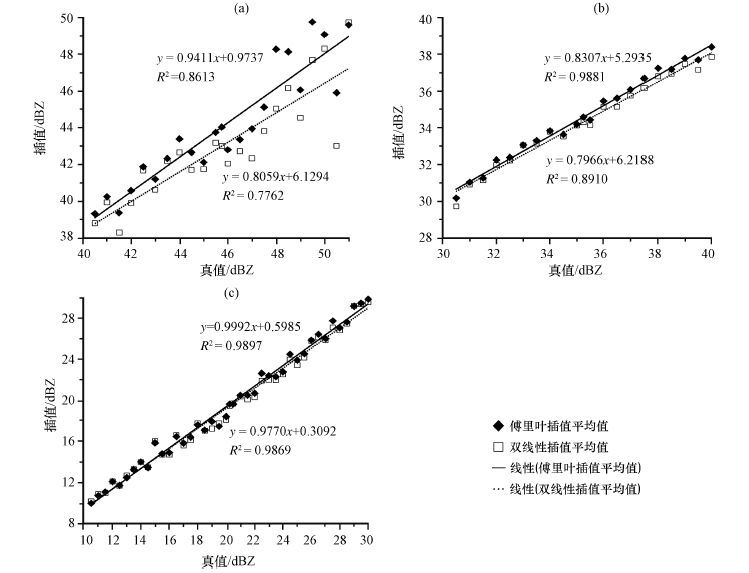
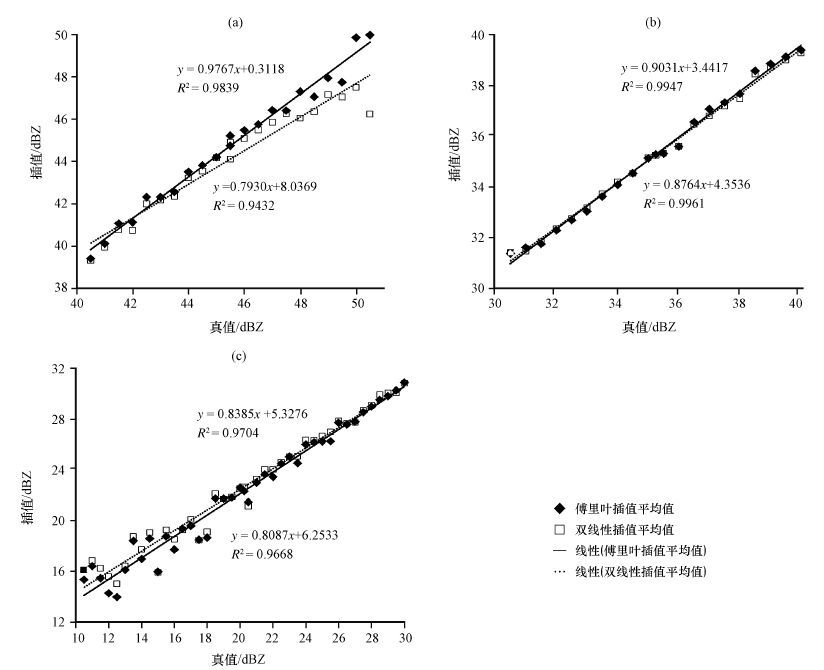
为了进一步表达傅里叶插值的这一优势,把图 3a中所有像素的回波强度作为真值,对图 3c和3d分别进行像素一一配对比较,得到真值40 dBZ以上的像素与图 3c和3d中的对应像素值的统计表如表 1所示。表 1中数据含义以第1行为例,真值为40. 5 dBZ的像素在图 3a中有58个,对应的这58个像素在图 3d中的值(即傅里叶插值)的平均值为39. 4 dBZ、标准差为1. 9 dBZ,而它们在在图 3c中的值(即双线性插值)的平均值为39. 3 dBZ、标准差为2. 1 dBZ,即,对于真值为40. 5 dBZ的58个像素而言,两种插值法得到的结果无明显差异,但傅里叶插值平均值更接近于真值,这表明傅里叶插值法优于双线性插值法。由表 1中各行数据可见,随着真值增大(即真实的回波强度增强),傅里叶插值法优于双线性插值法更加明显。表 1中最后一行数据表明,真值40 dBZ以上的像素共有672个,平均45. 5 dBZ,傅里叶插值平均值为44. 8 dBZ、标准差为1. 6 dBZ,双线性插值平均值为44. 1 dBZ、标准差为1. 5 dBZ。因此,可以说,在“较强回波区”,两种插值法得到的结果从标准差看无明显差异,但傅里叶插值平均值更接近于真值,这表明傅里叶插值法优于双线性插值法。这一判断还可以从由表 1制作的图 4a看出,实线框内为傅里叶插值法的拟合方程和拟合度,虚线框内为双线性插值法的。由图 4a可见,傅里叶插值平均值与真值有更好的一致性(拟合度R2较大,在0. 98以上; 拟合线斜率更接近于1,截距更接近于0 dBZ),而双线性插值与真值之间的一致性就差一些(拟合度较小,为0. 94; 拟合线斜率也较小,仅为0. 79,而截距较大,接近8. 04 dBZ)。
| 表 1 图 3a中真值40 dBZ以上的像素与图 3c和3d中的对应像素值的对比统计 Table 1 Comparison of statistics between pixels over 40 dBZ in figure 3a and corresponding pixels in figure 3c and 3d |
|
图 4 个例1插值平均值对比真值范围:(a)40. 5~51 dBZ,(b)30. 5~40 dBZ,(c)10. 5~30 dBZ Figure 4 Comparison of average value for Case one. True value range:(a)40. 5~51 dBZ,(b)30. 5~40 dBZ,(c)10. 5~30 dBZ |
同理,把图 3a中真值在30~40 dBZ 范围内的像素(即中等强度回波区)与图 3c、d中的对应像素值进行对比统计并作拟合分析,可得到图 4b; 把图 3a中真值在10~30 dBZ范围内的像素(即弱回波区)与图 3c、d中的对应像素值进行对比统计并作拟合分析,可得到图 4c; 10 dBZ以下的像素点由于个数较少,且对天气影响较小,所以不对其进行对比。由图 4b、c的散点分布及其拟合参数可见,在较强回波区周围的中等强度和弱回波区,两种插值方法的效果差异不大。
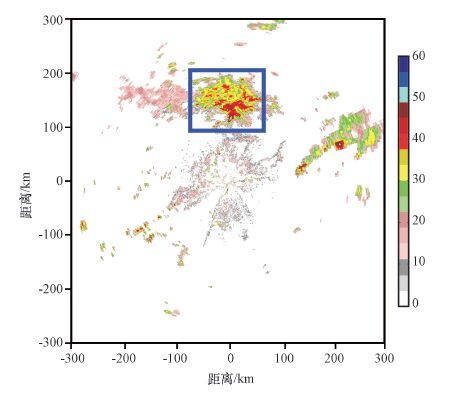
3.2 个例2图 5为2013年8月24日21:33南京SA雷达0. 5°仰角PPI回波图,当时洪泽湖地区出现了中到大雨(蓝色方框区域)。类似于对个例1的强对流区实验,得到图 5蓝色方框区的插值实验结果如图 6所示。图 6a~d之间的差异特征,与个例1结果(图 3a~d)的差异特征基本相同,从整体图像上来看,傅里叶插值处理后的图像与原分辨率雷达回波图更一致。仿照图 4,得到个例2不同回波强度区的插值平均值散点图及其拟合线(图 7)。由图 7a可见,在强回波区,傅里叶插值效果明显优于双线性插值(拟合度、拟合线斜率及截距都明显),而在强回波区周围的中等强度和弱回波区,两种插值效果基本相同。这与个例1的结论相同。
|
图 5 2013年8月24日21:33南京SA雷达0. 5°仰角PPI回波分布(单位: dBZ) Figure 5 Radar echo PPI at 0. 5° elevation of Nanjing SA radar at 21:33 on 24 August 2013. Unit: dBZ |
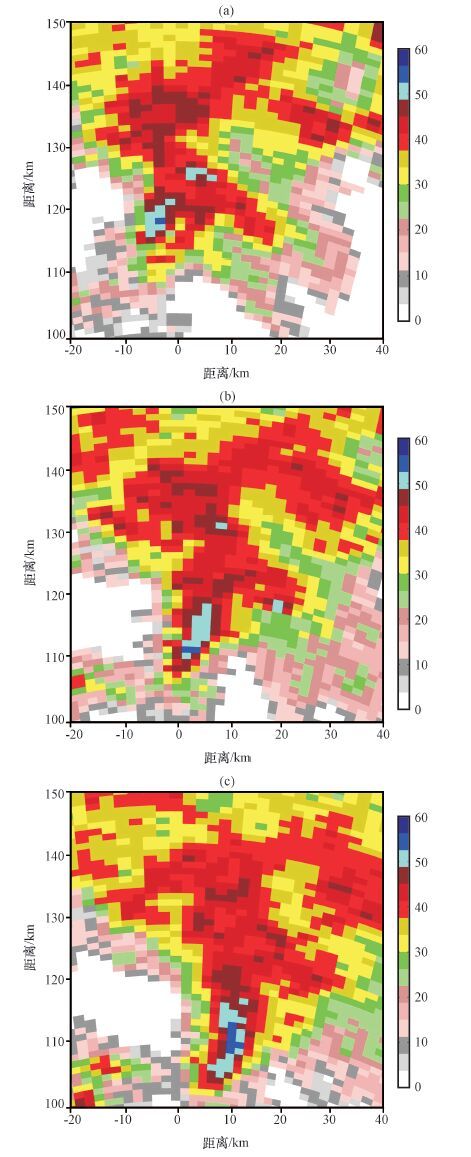
利用傅里叶插值法能凸显出强回波中心及位置的优势,本文以个例2(2013年8月24日21:33)PPI图为参照,获得了其前后时间分别为21:15和21:51的PPI图像,放大强回波区后如图 8,对这三幅PPI回波图中的强对流区域基数据分别进行傅里叶插值,将分辨率在径向和切向上分别提高两倍,得到强回波区的结果如图 9所示。对比图 8,傅里叶插值法使强回波中心更加突出,从图 9a中可明显的看到强回波区A、B和强回波点C,其中区域A的强回波特征最为突出(深蓝色),强度在53 dBZ以上。经过18 min的演变,如图 9b,区域A和C合并增强,范围不断扩大,强回波中心(深蓝色点),较图 9a中的点向东南方向移动了约8 km; 区域B回波逐渐减弱、消失、变为深红色,回波强度<48. 5 dBZ; 区域D为新生强回波区,强度比图 8b显示的要强。图 9c中,区域A的强回波仍在加强、形成弓状,强回波(深蓝色)面积继续增大,继续向东南方向移动了约8 km,移动速度约为7. 8 m·s-1; 区域B已完全消失,区域D也在减弱。从图 9还可看出,E、F等一些强回波点,并且强回波点C、F在图 8中是没有显示的。
|
图 8 2013年8月2日南京SA雷达0. 5°仰角不同时刻的PPI强回波分布(单位: dBZ) (a)21:15,(b)21:33,(c)21:51 Figure 8 Strong echo PPI at 0. 5° elevation of Nanjing SA radar on 24 August 2013. Unit: dBZ. (a)At 21:15,(b)at 21:33,(c)at 21:51 |
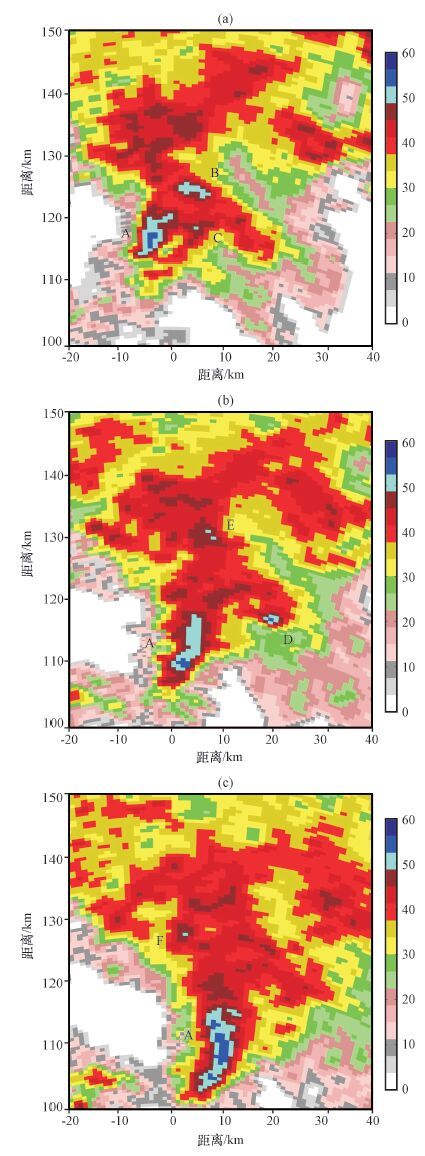
|
图 9 2013年8月24日不同时刻傅里叶插值后的强回波区域(单位: dBZ) (a)21:15,(b)21:33,(c)21:51 Figure 9 Strong echo by Fourier interpolation in different duration on 24 August 2013. Unit: dBZ. (a)At 21:15,(b)at 21:33,(c)at 21:51 |
以上分析更加证明了傅里叶插值法能突出强回波中心及位置的特征,使强回波内部的结构更加具体、细化,并且根据凸显出的强回波中心点的移动可以更好地估计出回波的移动速度矢量,为进一步提高临近预报水平提供帮助。
4 结语本文提出了一种基于傅里叶谱分析的雷达回波强度图像插值方法。插值方法的原理和个例实验都表明,双线性插值法在处理雷达数据时,会因为该方法的“平均”过程而缩小强回波区域的范围,而傅里叶插值法利用了谱分析和重采样的性质,可在一定程度上避免这个问题。
在处理适当距离处具有波动特征、产生对流性降水的“积状云”回波时,傅里叶插值法能凸显出强回波区的结构特征,尤其是能够在距离雷达较远处插值出因雷达分辨率低而探测不到的强回波中心(从效果上看,有“捏造”强回波中心的能力),这对于强回波区及其中心识别而言,傅里叶插值效果优于双线性插值法。在处理强回波区周围的回波较弱、分布较为平缓的雷达资料时,傅里叶插值效果与双线性插值法差异不明显,虽然也会“捏造”出强回波中心,但由于其周围回波都很弱,这种“捏造”的强回波中心并不会达到强对流天气回波的强度,因此不会影响对强对流区的识别。
利用傅里叶插值法的优势,可对一个天气过程中的雷达回波图像序列进行傅里叶插值处理,有助于更细致地分析强回波结构、位置及其发展情况,并且可以根据凸显出的强回波中心点的位置计算出回波移动的速度矢量,为进一步提高雷达数据临近预报应用效果提供帮助。
当然,由于雷达PPI数据中每插值一个点,双线性插值的计算所涉及数据只有4个,而傅里叶插值计算需要涉及整个PPI的数据,所以傅里叶插值方法的耗时与中间内存要比双线性插值法多一些,但这一要求对于现在计算机的性能和水平,是不成问题的。另外,由于本文所提出的傅里叶插值方法的主要优势是利于突出产生对流性降水的积状云“强回波中心和位置”,对“弱回波区”以及分布比较均匀的层状云,内插效果与双线性方法差异不大,故在考虑时间和内存需求时,可以先进行粗略的回波性质判别,傅里叶插值方法只针对积状云强回波区。
| Askelson M A, Aubagnac J P, Straka J M. 2000. An adaptation of the Barnes filter applied to the objective analysis of radar data[J]. Mon Wea Rev, 128 : 3050–3082. DOI:10.1175/1520-0493(2000)128<3050:AAOTBF>2.0.CO;2 | |
| Fulton R. 1998. WSR-88D polar to HRAP mapping[Z]. Tech Memo, Hydrology Research Laboratory, Office of Hydrology, National Weather Service, Silver Spring, MD, 33. | |
| Jorgensen D P, Hildebrand P H, Frush C L. 1983. Feasibility test of an airborne pulse-Doppler meteorological radar[J]. J Appl Meteor, 22 : 744–757. DOI:10.1175/1520-0450(1983)022<0744:FTOAAP>2.0.CO;2 | |
| Miller L J, Mohr C G, Weinheimer A J. 1986. The simple rectification to Cartesian space of folded radial velocities from Doppler radar sampling[J]. J Atmos Oceanic Tech, 3 : 162–174. DOI:10.1175/1520-0426(1986)003<0162:TSRTCS>2.0.CO;2 | |
| Mohr C G, Vaughn R L. 1979. An economical procedure for Cartesian interpolation and display of reflectivity factor data in three-dimensional space[J]. J Appl Meteor, 18 : 661–670. DOI:10.1175/1520-0450(1979)018<0661:AEPFCI>2.0.CO;2 | |
| Serafin R J, Wilson J W. 2000. Operational weather radar in the United States:Progress and opportunity[J]. Bull Amer Meteor Soc, 81 : 501–518. DOI:10.1175/1520-0477(2000)081<0501:OWRITU>2.3.CO;2 | |
| Shapiro A, Robinson P, Wurman J, et al. 2003. Single-Doppler velocity retrieval with rapid-scan radar data[J]. J Atmos Oceanic Tech, 20 : 1758–1775. DOI:10.1175/1520-0426(2003)020<1758:SVRWRR>2.0.CO;2 | |
| Weygandt S S, Shapiro A, Droegemeier K K. 2002. Retrieval of model initial fields from single-Doppler observations of a supercell thunderstorm[J]. Part I:Single-Doppler velocity retrieval[J]. Mon Wea Rev, 130 : 433–453. | |
| 段艺萍, 刘寿东, 刘黎平, 等. 2014. 新一代天气雷达三维组网产品在人工防雹的应用[J]. 高原气象 , 33 (5): 1426–1439. DOI:10.7522/j.issn.1000-0534.2013.00139 Duan Yiping, Liu Shoudong, Liu Liping, et al. 2014. Application of CINRAD mosaic products on artificial hail suppression[J]. Plateau Meteor, 33 (5): 1426–1439. DOI:10.7522/j.issn.1000-0534.2013.00139 | |
| 黄嘉佑. 2000. 气象统计分析与预报方法[M]. 北京: 气象出版社, 309-343. Huang Jiayou. 2000. Meteorological statistical analysis and prediction method[M]. Beijing: Meteorological Press , 309-343. | |
| 黄云仙, 张英. 2008. 多普勒天气雷达数据插值方法比较研究[J]. 遥感信息 , 23 (2): 39–45. Huang Yunxian, Zhang Ying. 2008. Comparison of interpolation schemes for the Doppler Weather Radar data[J]. Remote Sensing Informatin, 23 (2): 39–45. | |
| 李柏, 古庆同, 李瑞义, 等. 2013. 新一代天气雷达灾害性天气监测能力分析及未来发展[J]. 气象 , 39 (3): 265–280. Li Bai, Gu Qingdong, Li Ruiyi, et al. 2013. Analyses on disastrous weather monitoring capability of CINRAD and future development[J]. Meteor Mon, 39 (3): 265–280. | |
| 刘杰, 许小峰, 罗慧. 2012. 极端天气气候事件影响我国农业经济产出的实证研究[J]. 中国科学:地球科学 , 42 (7): 1076–1082. Liu Jie, Xu Xiao Feng, Luo Hui. 2012. An empirical research on the impacts of extreme weather and climate events on agricultural economic output in China[J]. Sci Sin Terrae, 42 (7): 1076–1082. | |
| 王庆东, 严卫, 马宁. 2002. 数字化天气雷达组网拼图算法[J]. 解放军理工大学学报:自然科学版 , 3 (2): 90–93. Wang Qingdong, Yan Wei, Ma Ning. 2002. Algorithm for digital weather radar networking and composite image[J]. Journal of PLA University of Science and Technology:Natural Science Edition, 3 (2): 90–93. | |
| 王振会, 张培昌. 2001. 天气雷达回波衰减订正算法的研究(Ⅱ):数值模拟与个例实验[J]. 高原气象 , 20 (2): 115–120. Wang Zhenhui, Zhang Peichang. 2001. A study on the algorithm making attenuation correction to observations of radar reflectivity factor (II):Numerical simulations and a case study[J]. Plateau Meteor, 20 (2): 115–120. | |
| 温颖, 赵阳, 赵果, 等. 2015. 台风"莫拉克"登陆过程的闪电活动与雷达回波特征[J]. 高原气象 , 34 (3): 832–841. DOI:10.7522/j.issn.1000-0534.2015.0036 Wen Ying, Zhao Yang, Zhao Guo, et al. 2015. Characteristics of lightning activity and radar reflectivity during typhoon ‘Morakot’ landfall[J]. Plateau Meteor, 34 (3): 832–841. DOI:10.7522/j.issn.1000-0534.2015.0036 | |
| 肖现, 肖辉, 王振会, 等. 2008. 傅立叶相位技术在雷达回波移动矢量特征分析中的应用[J]. 南京气象学院学报 , 30 (4): 473–482. Xiao Xian, Xiao Hui, Wang Zhenhui, et al. 2008. Applications of Fourier phase analysis technique to computation of radar cloud echo motion vectors[J]. J Nanjing Insti Meteor, 30 (4): 473–482. | |
| 肖艳姣, 刘黎平. 2006. 新一代天气雷达网资料的三维格点化及拼图方法研究[J]. 气象学报 , 64 (5): 647–657. Xiao Yanjiao, Liu Liping. 2006. Study of methods for interpolating data from weather radar network to 3-D grid and mosaics[J]. Acta Meteor Sinica, 64 (5): 647–657. | |
| 杨吉, 刘黎平, 李国平, 等. 2012. 基于雷达回波拼图资料的风暴单体和中尺度对流系统识别、跟踪及预报技术[J]. 气象学报 , 70 (6): 1347–1355. Yang Ji, Liu Liping, Li Guoping, et al. 2012. A new techniques for storm cell and mesoscale convective systems identification, tracking and nowcasting based on the radar mosaic data[J]. Acta Meteor Sinica, 70 (6): 1347–1355. | |
| 翟盘茂, 刘静. 2012. 气候变暖背景下的极端天气气候事件与防灾减灾[J]. 中国工程科学 , 14 (9): 55–63. Zhai Panmao, Liu Jing. 2012. Extreme weather/climate events and disaster prevention and mitigation under global warming background[J]. Engineering Sciences, 14 (9): 55–63. | |
| 张红, 王振会, 许建明. 2006. 利用静止卫星云图进行二维傅里叶相位导风试验[J]. 高原气象 , 25 (1): 105–109. Zhang Hong, Wang Zhenhui, Xu Jianming. 2006. An experiment to derive cloud motion vectors from satellite images with 2-D Fourier phase analysis technique[J]. Plateau Meteor, 25 (1): 105–109. | |
| 张蕾, 王振会, 杨艳蓉. 2011. 多普勒天气雷达资料在数值模式ARPS中的试验[J]. 气象科学 , 31 (5): 567–575. Zhang Lei, Wang Zhenhui, Yang Yanrong. 2011. Application test of Doppler radar data in numerical model ARPS[J]. J Meteor Sci, 31 (5): 567–575. | |
| 张培昌, 王振会. 2001. 天气雷达回波衰减订正算法的研究(Ⅰ):理论分析[J]. 高原气象 , 20 (1): 1–5. Zhang Peichang, Wang Zhenhui. 2001. A study on algorithm to make attenuation correction to radar observations of radar reflectivity factor(Ⅰ):Theoretical analysis[J]. Plateau Meteor, 20 (1): 1–5. | |
| 张培昌. 1989. 天气雷达组网拼图的四维同化方法[J]. 南京气象学院学报 , 12 (3): 22–28. Zhang Peichang. 1989. 4-D assimilation method of weather radar network[J]. J Nanjing Insti Meteor, 12 (3): 22–28. | |
| 张沛源, 杨洪平, 胡绍萍. 2008. 新一代天气雷达在临近预报和灾害性天气警报中的应用[J]. 气象 , 34 (1): 3–11. Zhang Peiyuan, Yang Hongping, Hu Shaoping. 2008. Applications of new generation weather radar to nowcastingand warning of severe weather[J]. Meteor Mon, 34 (1): 3–11. | |
| 张一平, 俞小鼎, 孙景兰, 等. 2014. 一次槽后型大暴雨伴冰雹的形成机制和雷达观测分析[J]. 高原气象 , 33 (4): 1093–1104. DOI:10.7522/j.issn.1000-0534.2012.00200 Zhang Yiping, Yu Xiaoding, Sun Jinglan, et al. 2014. Formation mechanism and analysis of radar observation of a heavy rainstorm accompanied by hail that back of trough[J]. Plateau Meteor, 33 (4): 1093–1104. DOI:10.7522/j.issn.1000-0534.2012.00200 | |
| 张之贤, 张强, 赵庆云, 等. 2014. 陇东南地区短时强降水的雷达回波特征及其降水反演[J]. 高原气象 , 33 (2): 530–538. DOI:10.7522/j.issn.1000-0534.2013.00001 Zhang Zhixian, Zhang Qiang, Zhao Qingyun, et al. 2014. Analysis on radar echo and precipitation retrieve of short-duration heavy precipitation in Southeast Gansu[J]. Plateau Meteor, 33 (2): 530–538. DOI:10.7522/j.issn.1000-0534.2013.00001 | |
| 邹海波, 单九生, 邓诗茹. 2014. 多普勒雷达资料的网格化研究[J]. 气象与减灾研究 , 35 (2): 23–30. Zou Haibo, Shan Jiusheng, Deng Shiru. 2014. Study of the Doppler radar data gridding[J]. Meteor Disaster Reduction Research, 35 (2): 23–30. |
2. School of Atmospheric Physics, Nanjing University of Information Science & Technology, Nanjing 210044, China
 2016, Vol. 35
2016, Vol. 35