2. 中国科学院大学, 北京 100101;
3. 青藏高原环境变化与地表过程重点实验室, 北京 100101;
4. 中国科学院青藏高原地球科学卓越创新中心, 北京 100101
近年来, 由于人类活动的干扰, 大气污染和温室气体的浓度逐渐升高, 全球气候变化研究现已成为国际科学界的热点之一 (张志强和孙成权, 1999; Qin et al, 2005; Wu et al, 2005; Wang et al, 2006; 鲍媛媛和康志明, 2014; 王青霞等, 2014)。气候变化特别是气温和降水的变化对水资源的影响已有了大量研究 (刘颖秋, 2002; 朱利和张万昌, 2005; 任国玉等, 2008; 岑思弦等, 2014; 程慧萍和贾晓静, 2014), 就水资源平衡关系而言, 影响水资源变化的不仅仅是气温和降水, 其他气候要素对水资源的变化也具有很重要的作用。蒸发是水循环中的重要组成部分, 它和降水、径流一起决定着一个地区的水量平衡 (曾燕等, 2007; 张存厚等, 2007)。同时, 全球性陆面蒸发对大气环流和降水均有重要影响意义, 因此, 在全球气候变化背景下, 对于蒸发的研究具有重要意义。
当全球平均气温升高时, 通常认为空气将变得干燥, 陆面水体蒸发量增大, 全球水循环加速 (杜军等, 2008)。目前, 已经观测到北半球1950-2000年区域平均气温以0.15 ℃·(10a)-1的速率增温 (Houghton and Ding, 2001), 但通过对蒸发皿蒸发量变化的分析, 人们认为全球许多地区的蒸发皿蒸发量存在显著的下降趋势 (Peterson, 1995; Cohen et al, 2002; 丛振涛等, 2008)。Roderick and Farquhar (2002)将全球气温升高与潜在蒸散量减少同时发生的水文气候现象称为“蒸发悖论”。目前, 已经有研究表明青藏高原 (下称高原) 地区也存在“蒸发悖论”现象 (Zhang et al, 2007; 李景玉等, 2009; Liu et al, 2011)。Brutsaert and Parlange (1998)指出, 确定蒸发皿蒸发量与实际蒸散发量的关系是解决“蒸发悖论”的关键。所以, 众多学者开展了“蒸发悖论”的相关研究以及蒸发皿蒸发量与实际蒸散发量的关系研究。
目前, 对于“蒸发悖论”的解释, 有一种观点是认为蒸发皿蒸发量与实际蒸散发量存在互补关系, 也就是说, 蒸发皿蒸发量下降而实际蒸散发量增加 (Bouchet, 1963; Brutsaert and Parlange, 1998; Hobbins et al, 2004; Ramírez, 2005; Zhang et al, 2007; 张小磊和杨梅学, 2010)。Bouchet (1963)指出, 在实际蒸散发量和潜在蒸发量之间存在一种互补反馈机制, 随着环境湿度的增加, 实际蒸散发量增加而潜在蒸发量下降, 并在湿环境下趋于相等。Ma (2015)利用2013年6-9月的气象观测资料, 评估了互补理论在青藏高原高寒草甸区的应用。
本文将在参考前人研究方法的基础上, 应用互补理论分析中国西藏地区中国科学院珠穆朗玛大气与环境综合观测研究站实际蒸散和蒸发皿蒸发量之间的关系。
2 资料选取和方法介绍 2.1 资料选取青藏高原是亚欧大陆上最大的地貌单元, 位于中国西南部, 毗邻印度, 从东到西约1900 km, 从南到北约100 km, 总面积约为120×104 km2。高原平均海拔4000 m以上, 由藏南谷地、藏北高原、川藏高山峡谷所组成。中国科学院珠穆朗玛大气与环境综合观测研究站 (简称“珠峰站”, 28.21°N, 86.56°E, 海拔4276 m), 位于高原地区定日县扎西宗乡巴松村, 距登山大本营40 km左右。观测站建在河谷中, 地势较为平坦、开阔, 下垫面类型为戈壁, 地表以戈壁裸地为主, 植被稀疏、矮小。观测场内设有大气边界层气象塔、LAP3000风温廓线仪、超声风温仪以及降水量、20 cm直径的蒸发皿蒸发量观测等 (图 1)。

|
图 1 珠峰站下垫面及仪器设置 Figure 1 Underlying surface and instrument in Qomolangma station |
所用到的观测数据为蒸发皿蒸发量, 风速, 温度, 相对湿度, 净辐射, 潜热通量, 感热通量, 土壤热通量。其中, 蒸发皿蒸发量的观测频率为每天一次, 其余参数为每30 min一次。所用数据观测时段为2010年全年。
实际蒸散发量是由气温和潜热通量计算得到的, 由于使用的气温和潜热通量观测数据是每30 min观测一次, 所以首先计算得到实际蒸散发量的瞬时值, 并剔除异常值; 然后计算日总量, 如果一天的缺测数据多于25个, 则舍弃这一天的观测数据, 并且, 如果这一天的观测数据都集中在白天或者都集中在夜间, 则这一天的数据也要舍弃。
净辐射和土壤热通量的日均值计算, 首先计算每小时的平均值, 然后对没有缺测值的月份直接进行月平均计算, 对于有缺测值的月份, 首先选取每天02:00(北京时, 下同) 到24:00每间隔2 h时刻的观测值, 然后计算其平均值; 如果一天内这12个时刻存在缺测值, 则选取02:00到24:00每间隔4 h时刻的观测值, 然后计算其平均值; 如果一天内这6个时刻仍然存在缺测值, 则选取02:00和14:00观测值的平均值, 然后计算其平均值。
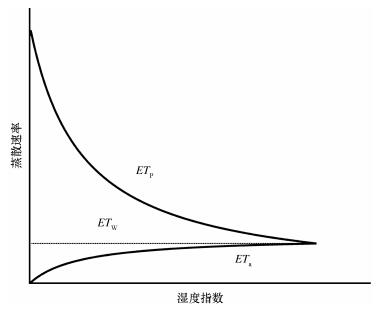
2.2 分析方法Bouchet (1963)指出, 在实际蒸散发量和潜在蒸发量之间存在一种互补反馈机制 (图 2), 实际蒸散发量和潜在蒸发量在湿环境下趋于相等, 并且等于湿环境下的蒸散量, ETa=ETp=ETw。潜在蒸发速率和实际蒸发速率之间存在如下关系:
|
图 2 互补理论的概念表示 Figure 2 Conceptual representation of the complementary relationship |
| $ E{{T}_{\text{p}}}-E{{T}_{\text{w}}}=\varepsilon \left(E{{T}_{\text{w}}}-E{{T}_{a}} \right), $ | (1) |
其中: ETp为潜在蒸发速率 (单位: mm·d-1), ETa为实际蒸散速率 (单位: mm·d-1), ETw为湿环境下的蒸发速率 (单位: mm·d-1), ε为使潜在蒸发量增加的那部分感热的比例。
根据公式 (1) 可以得到:
| $ \frac{E{{T}_{\text{a}}}}{E{{T}_{\text{w}}}}=\frac{\left(1+\varepsilon \right)\frac{E{{T}_{\text{a}}}}{E{{T}_{\text{p}}}}}{1+\varepsilon \frac{E{{T}_{\text{a}}}}{E{{T}_{\text{p}}}}}, $ | (2) |
| $ \frac{E{{T}_{\text{p}}}}{E{{T}_{\text{w}}}}=\frac{1+\varepsilon }{1+\varepsilon \frac{E{{T}_{\text{a}}}}{E{{T}_{\text{p}}}}}, $ | (3) |
首先进行数据的标准化, ETa/ETw=ETa+, ETp/ETw=ETp+, ETa/ETp=ETHI, ETa+和ETp+分别为标准化后的实际蒸散发和潜在蒸发速率, ETHI为湿度指数。代入公式 (2) 和 (3), 得到:
首先进行数据的标准化, ETa/ETw=ETa+, ETp/ETw=ETp+, ETa/ETp=ETHI, ETa+和ETp+分别为标准化后的实际蒸散发和潜在蒸发速率, ETHI为湿度指数。代入公式 (2) 和 (3), 得到:
| $ E{{T}_{\text{a+}}}=\frac{\left(1+\varepsilon \right)E{{T}_{\text{HI}}}}{1+\varepsilon E{{T}_{\text{HI}}}}, $ | (4) |
| $ E{{T}_{\text{p+}}}=\frac{1+\varepsilon }{1+\varepsilon E{{T}_{\text{HI}}}}, $ | (5) |
据Brutsaert and Stricker (1979)的研究, ETp可以根据Penman (1948)公式计算:
| $ E{{T}_{\text{p}}}=\frac{\Delta \left(Rn-G \right)}{\Delta +\gamma }+\frac{\gamma f\left(U \right)\left({{e}_{0}}-{{e}_{a}} \right)}{\Delta +\gamma }, $ | (6) |
其中: ETp为潜在蒸发速率 (单位: mm·d-1)Δ为饱和水汽压随温度变化的斜率 (单位: kPa·℃-1), γ为干湿表常数 (单位: kPa·℃-1), Rn和G分别表示净辐射和土壤热通量 (单位: mm·d-1), e0和ea分别为饱和水汽压和实际水汽压 (单位: kPa), f(U) 为Rome风速方程 (Penman, 1948):
| $ f\left(U \right)=2.6\left(1+0.54{{U}_{2}} \right), $ | (7) |
其中: U2为观测高度 (3.25 m) 处的风速 (单位: m·s-1), f(U) 的单位为mm·d-1·kPa。
由于蒸发皿蒸发量 (Epan) 是潜在蒸发量 (ETp) 的很好的代用指标 (Zhang et al, 2007), 并且存在如下关系:
| $ E{{T}_{\text{p}}}=cE{{T}_{\text{pan}}}, $ | (8) |
其中: c表示蒸发皿系数, c值大小不仅受环境条件的影响, 而且受蒸发皿型号不同的影响。在不同的文章中c有不同的取值 (Pettijohn and Salvucci, 2009; Brutsaert, 2013), 本文c取值为1(Priestley, Taylor, 1972; Kahler and Brutsaert, 2006; Szilagyi, 2007; Pettijohn and Salvucci, 2009; Ma et al, 2015), 原因主要有两个方面:一方面, 本文希望通过互补理论得出珠峰站蒸发皿蒸发量和实际蒸散发量之间的关系, 从而为实际蒸散发量的计算提供一些参考, 并不是为了得出青藏高原不同地区的不同的c值; 另一方面, 在公式 (1) 中, 当cEpan代替了ETp, 对于实际蒸散发量的估算可以由ε进行校准 (Kahler and Brutsaert, 2006; Ma et al, 2015)。
ETw为湿环境下的蒸发速率 (单位: mm·d-1), 有如下定义 (Priestley and Taylor, 1972; Ma et al, 2015):
| $ E{{T}_{\text{w}}}=\alpha \frac{{{\Delta }_{\text{wea}}}\left(Rn-G \right)}{{{\Delta }_{\text{wea}}}+\gamma }, $ | (9) |
其中: α为泰勒系数, 取值1.26(Priestley and Taylor, 1972; Ma et al, 2015), Δwea(单位: kPa·℃-1) 为饱和水汽压随湿环境下的温度Twea变化的斜率, 其他参数的物理意义及单位与公式 (6) 中相同。
βwe为湿环境下的波文比, 根据如下公式可以计算Twea(Ma et al, 2015):
| $ {{\beta }_{\text{we}}}=\frac{Rn-G-E{{T}_{\text{p}}}}{E{{T}_{\text{p}}}}\approx \gamma \frac{{{T}_{\text{wea}}}-{{T}_{a}}}{{{e}_{0}}\left({{T}_{\text{wea}}} \right)-{{e}_{a}}}, $ | (10) |
其中, Twea为湿空气下的温度, Ta为气温, e0(Twea) 为在Twea时的的饱和水汽压, ea为在气温Ta下的实际水汽压。
最后将标准化后的ETa+和ETp+以及ETw带入公式 (1) 计算得出的ε, 然后进行实际蒸散发量 (ETa-sim) 的计算:
| $ E{{T}_{\text{a-sim}}}=\left(1+\varepsilon \right)E{{T}_{\text{w}}}/\varepsilon -E{{T}_{\text{p}}}/\varepsilon . $ | (11) |
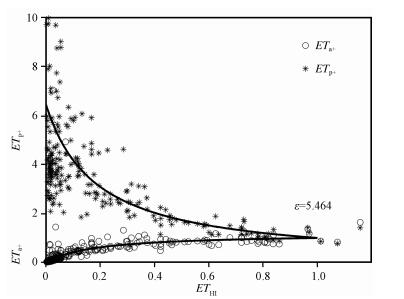
图 3为标准化的实际蒸散发和潜在蒸发速率随湿度指数ETHI的变化。图中显示标准化后的实际蒸散发和潜在蒸发速率随湿度指数增加而趋近于同一个值, 根据公式 (1) 计算得出ε=5.464, 图 3中的曲线是根据ε=5.464和公式 (4) 和 (5) 计算得到的。由公式 (11) 计算得出ETa-sim, 并对ETa-sim和ETa进行对比 (图 4)。
|
图 3 标准化的实际 (ETa+) 和潜在 (ETp+) 蒸散速率随湿度指数ETHI的变化 图中的曲线是根据ε=5.464和公式 (4) 和 (5) 计算得到 Figure 3 Normalized daily actual, ETa+(=ETa/ETw), and estimated potential, ETp+(=ETp/ETw), evapotranspiration rates plotted against ETHI.The curves representformula (4) and (5) with a calibrated value of 5.464 for ε |
|
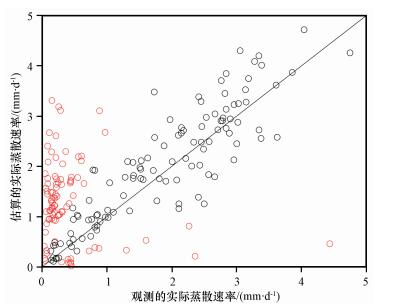
图 4 2010年珠峰站观测 (ETa) 和计算 (ETa-sim) 的实际蒸散发速率对比 ETa-sim是根据公式 (11) 计算得到的, 其中ETp=cEpan(c=1), ε=5.464, 实际蒸散发量的计算值比较接近于观测值的点用黑色表示, 差距比较大的点用红色表示 Figure 4 Comparison of daily observed (ETa) and simulated (ETa-sim) actual evapotranspiration rates in 2010 at Qomola-ngma Station.ETa-sim is from (11) with ETp=cEpan, c=1, and calibrated values of ε=5.464.Black dots indicate the calculated actual evapotranspiration is more close to the observed value, red dots indicate the calculated actual evapotranspiration is not close to the observed value |
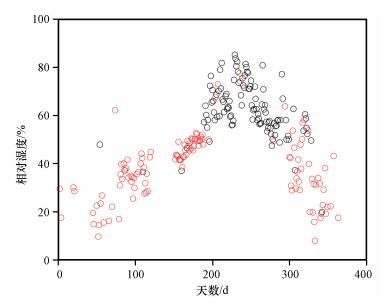
如图 4所示, 部分ETa的计算结果不甚理想, 根据图 5, 这些点主要出现在相对湿度比较小的区域, 这可能是由于相对湿度比较小的时候互补理论的应用效果不好造成的, 为考察互补理论在不同环境湿度条件下的适用性, 本文根据珠峰站2010年全年相对湿度变化情况 (图 5), 将相对湿度>50%的月份 (7-10月) 定义为湿季, < 50%的月份 (1-6月, 11-12月) 定义为干季:
|
图 5 2010年珠峰站相对湿度的变化 红色点表示实际蒸散发量的计算值与观测值之间的差距比较大 Figure 5 Relative humidity varies with date in 2010 at Qomolangma station.Red dots indicate the calculated actual evapotranspiration is not close to the observed value |
分别作出湿季 (7-10月) 标准化后的实际蒸散速率ETa+_wet和潜在蒸发速率 (由cEpan代替, c取值为1)ETp+_wet随ETHI_wet的变化曲线, 以及干季 (1-6月, 11-12月)ETa+_dry和ETp+_dry随ETHI_dry的变化曲线, 最后根据公式 (11) 计算得出湿季ETa-sim_wet和干季ETa-sim_dry, 分别对ETa-sim_wet、ETa-sim_dry与实际蒸散发的观测值进行对比, 并对结果进行分析。
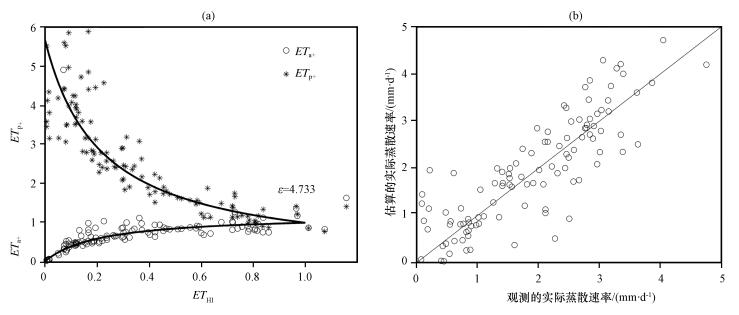
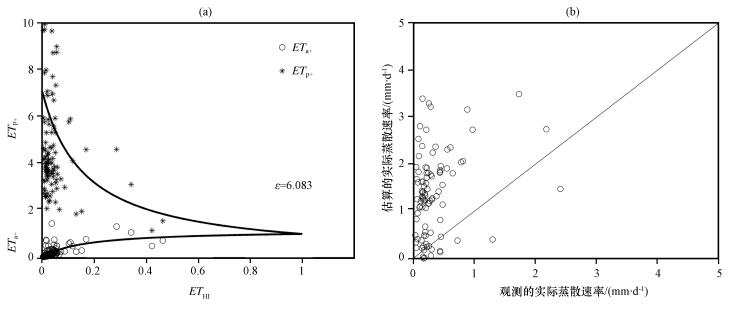
通过计算得到2010年珠峰站湿季的ε=4.733, 干季ε=6.083。图 6显示在湿季, 标准化后的实际蒸散发和潜在蒸发量随湿度指数的增加趋近于相等, 并且对实际蒸散发量的计算效果比较好; 图 7为干季, 标准化后的潜在蒸散量主要集中在湿度指数较小 (0~0.1) 的区域, 并且与湿度指数的变化未存在明显的线性关系, 实际蒸散发量的计算值远大于观测值。所以, 互补理论可能更适合用于湿季对实际蒸散发量的计算。
|
图 6 2010年7-10月珠峰站标准化的实际蒸散发和潜在蒸发速率随湿度指数的变化, 以及观测和计算的实际蒸散速率的对比 Figure 6 Normalized daily actual and estimated potential evapotranspiration rates plotted against ETHI, and comparison of daily observed and simulated actual evapotranspiration rates at Qomolangma station from 1 July to 30 October 2010 |
|
图 7 2010年1-6和11-12月珠峰站标准化的实际蒸散发和潜在蒸发速率随湿度指数的变化, 以及观测和计算的实际蒸散发速率的对比 Figure 7 Normalized daily actual and estimated potential evapotranspiration rates plotted against ETHI, and comparison of daily observed and simulated actual evapotranspiration rates at Qomolangma station from 1 January to 30 June and 1 November to 30 December 2010 |
为进一步理解应用互补理论计算干、湿季实际蒸散发量存在差异的原因, 本文又对蒸发皿蒸发量及实际蒸散发量的影响因子进行了分析。表 1和表 2为2010年珠峰站风速、气温、相对湿度、净辐射、降水分别与蒸发皿蒸发量和实际蒸散发量的多元回归分析 (均通过置信度为0.05的显著性检验)。从表 1和表 2中湿季的回归分析可以看出, 蒸发皿蒸发量主要受相对湿度影响, 并且随相对湿度的增加而减小, 随风速和温度的增加而增加; 实际蒸散发量受相对湿度影响也较大, 并且随相对湿度的增加而增加, 随风速和温度的增加而减小, 所以在湿季, 蒸发皿蒸发量和实际蒸散发量随气象因子的变化趋势相反, 并且受湿度指数的影响都较大, 所以随湿度指数的变化有明显的变化, 进而在湿季应用互补理论计算得到的实际蒸散发量更加接近于观测值。根据表 1可知, 蒸发皿蒸发量在干季主要受风速和温度影响, 受相对湿度的影响比较小, 所以随湿度指数的变化没有明显的变化, 造成在干季应用互补理论计算得到的实际蒸散发量与观测值的差距较大。所以互补理论可能比较适用于湿季, 在干季并不适用。
| 表 1 2010年珠峰站各气象要素分别与干季、湿季的蒸发皿蒸发量的多元回归系数 Table 1 Multiple regression coefficients of pan evaporation and meteorological elements in Qomolangma station in the dry season and wet seasonin 2010 |
| 表 2 2010年珠峰站各气象要素分别与干季、湿季的实际蒸散发量的多元回归系数 Table 2 Multiple regression coefficients of actual evaporation and meteorological elements in Qomolangma station in the dry season and wet season in 2010 |
(1) 根据互补理论首先得出了我国西藏地区珠峰站2010年的蒸发皿蒸发量和实际蒸散发量之间的关系, 湿季的ε值小于全年的ε值, 干季的ε值最大。
(2) 对实际蒸散发量进行了估算, 湿季实际蒸散发量的估算效果最好, 全年的计算效果较好, 干季的计算效果最差。
(3) 通过对珠峰站蒸发皿蒸发量和实际蒸散发量分别与风速、气温、相对湿度、净辐射、降水的关系分析, 结果表明:一方面, 在湿季蒸发皿蒸发量和实际蒸散发量随主要气象因子的变化趋势相反, 并且受湿度指数的影响都比较大, 进而随湿度指数的变化有明显的变化, 所以应用互补理论计算得到的实际蒸散发量更加接近于观测值; 另一方面, 蒸发皿蒸发量在干季主要受风速和温度影响, 受相对湿度影响比较小, 进而随湿度指数没有明显的变化, 所以在干季应用互补理论计算得到的实际蒸散发量与观测值的差距比较大。所以互补理论可能比较适用于湿季, 在干季并不适用。
| Bouchet R. 1963. Evapotranspiration réelle et potentielle, signification climatique[J]. IAHS Publ, 62: 134–142. | |
| Brutsaert W, Parlange M B. 1998. Hydrologic cycle explains the evaporation paradox[J]. Nature, 396(6706): 30–30. DOI:10.1038/23845 | |
| Brutsaert W, Stricker H. 1979. An advection-aridity approach to estimate actual regional evapotranspiration[J]. Water Resour Res, 15(2): 443–450. DOI:10.1029/WR015i002p00443 | |
| Brutsaert W. 2013. Use of pan evaporation to estimate terrestrial evaporation trends:The case of the Tibetan Plateau[J]. Water Resour Res, 49(5): 3054–3058. DOI:10.1002/wrcr.20247 | |
| Cohen S, Ianetz A, Stanhill G. 2002. Evaporative climate changes at Bet Dagan, Israel, 1964-1998[J]. Agri Forest Meteor, 111(2): 83–91. DOI:10.1016/S0168-1923(02)00016-3 | |
| Hobbins M T, Ramírez J A, Brown T C. 2004. Trends in pan evaporation and actual evapotranspiration across the conterminous US:Paradoxical or complementary?[J]. Geophys Res Lett, 31(13). | |
| Houghton J, Ding Y.2001.Climate Change:Scientific Basis[R].IPCC TAR Working Group, Cambridge University Press. | |
| Kahler D M, Brutsaert W. 2006. Complementary relationship between daily evaporation in the environment and pan evaporation[J]. Water Resour Res, 42(5): W05413. | |
| Liu X, Zheng H, Zhang M, et al. 2011. Identification of dominant climate factor for pan evaporation trend in the Tibetan Plateau[J]. J Geographical Sci, 21(4): 594–608. DOI:10.1007/s11442-011-0866-1 | |
| Ma N, Zhang Y, Szilagyi J, et al. 2015. Evaluating the complementary relationship of evapotranspiration in the alpine steppe of the Tibetan Plateau[J]. Water Resour Res, 51(2): 1069–1083. DOI:10.1002/2014WR015493 | |
| Penman H L. 1948. Natural evaporation from open water, bare soil and grass[J]. Proceedings of the Royal Society of London A:Mathematical, Physical and Engineering Sciences, 193(1032): 120–145. DOI:10.1098/rspa.1948.0037 | |
| Peterson T V. 1995. Evaporation losing its strength[J]. Nature, 377: 687–688. | |
| Pettijohn J C, Salvucci G D. 2009. A New Two-Dimensional Physical Basis for the Complementary Relation between Terrestrial and Pan Evaporation[J]. J Hydrometeor, 10(2): 565–574. DOI:10.1175/2008JHM1026.1 | |
| Priestley C H B, Taylor R J. 1972. On the assessment of surface heat flux and evaporation using large-scale parameters[J]. Mon Wea Rev, 100(2): 81–92. DOI:10.1175/1520-0493(1972)100<0081:OTAOSH>2.3.CO;2 | |
| Qin D, Ding Y, Su J, et al. 2005. Assessment of climate and environment changes in China (Ⅰ):Climate and environment changes in China and their projection[J]. Advances in Climate Change Research, 1(2): 1–5. | |
| Ramírez J A. 2005. Observational evidence of the complementary relationship in regional evaporation lends strong support for Bouchet's hypothesis[J]. Geophys Res Lett, 32(15): L15401. DOI:10.1029/2005GL023549 | |
| Roderick M L, Farquhar G D. 2002. The cause of decreased pan evaporation over the past 50 years[J]. Science, 298(5597): 1410–1411. | |
| Szilagyi J. 2007. On the inherent asymmetric nature of the complementary relationship of evaporation[J]. Geophys Res Lett, 34(2): L02405. DOI:10.1029/2006GL028708 | |
| Wang Y, Jiang T, Xu C, et al. 2006. Trend of Evapotranspiration over the Yangtze River Basin in 1961-2000[J]. Advances in Climate Change Research, 2(Suppl): 35–40. | |
| Wu S, Yin Y, Zhao H. 2005. Recongnition of ecosystem response to climate change impact[J]. Advances in Climate Change Research, 1(3): 115–118. | |
| Zhang Y, Liu C, Tang Y, et al. 2007. Trends in pan evaporation and reference and actual evapotranspiration across the Tibetan Plateau[J]. J Geophys Res, 112(D12): D12110. DOI:10.1029/2006JD008161 | |
| 鲍媛媛, 康志明. 2014. 2010年亚洲夏季风环流异常特征及其对中国雨带的影响[J]. 高原气象, 33(5): 1217–1228. DOI:10.7522/j.issn.1000-0534.2013.00099 Bao Yuanyuan, Kang Zhiming. 2014. Abnormal features of Asian summer monsoon circulation and its effects on Chinese rain band in 2010[J]. Plateau Meteor, 33(5): 1217–1228. DOI:10.7522/j.issn.1000-0534.2013.00099 | |
| 岑思弦, 巩远发, 赖欣. 2014. 青藏高原及其周围地区大气热源对川渝盆地夏季降水的影响[J]. 高原气象, 33(4): 1182–1189. DOI:10.7522/j.issn.1000-0534.2013.00122 Cen Sixian, Gong Yuanfa, Lai Xin. 2014. Impact of Heat Source over Qinghai-Xizang Plateau and Its Surrounding Areas on Rainfall in Sichuan-Chongqing Basin in Summer[J]. Plateau Meteor, 33(4): 1182–1189. DOI:10.7522/j.issn.1000-0534.2013.00122 | |
| 曾燕, 邱新法, 刘昌明, 等. 2007. 1960-2000年中国蒸发皿蒸发量的气候变化特征[J]. 水科学进展, 18(3): 311–318. Zeng Yan, Qiu Xinfa, Liu Changming, et al. 2007. Changes of pan evaporation in China in 1960-2000[J]. Adv Water Sci, 18(3): 311–318. | |
| 程慧萍, 贾晓静. 2014. 印度洋冬季海温异常对中国春季降水的影响[J]. 高原气象, 33(3): 733–742. DOI:10.7522/j.issn.1000-0534.2013.00024 Cheng Huiping, Jia Xiaojing. 2014. Influence of sea surface temperature anomalies of Indian Ocean in winter on precipitation over China in spring[J]. Plateau Meteor, 33(3): 733–742. DOI:10.7522/j.issn.1000-0534.2013.00024 | |
| 丛振涛, 倪广恒, 杨大文, 等. 2008. "蒸发悖论"在中国的规律分析[J]. 水科学进展, 19(2): 3–8. Cong Zhentao, Ni Guangheng, Yang Dawen, et al. 2008. Evaporation paradox in China[J]. Adv Water Sci, 19(2): 3–8. | |
| 杜军, 边多, 鲍建华, 等. 2008. 藏北高原蒸发皿蒸发量及其影响因素的变化特征[J]. 水科学进展, 19(6): 786–791. Du Jun, Bian Duo, Bao Jianhua, et al. 2008. Changes of pan evaporations and its impact factors over northern Tibet in 1971-2006[J]. Adv Water Sci, 19(6): 786–791. | |
| 李景玉, 张志果, 徐宗学, 等. 2009. 影响西藏地区蒸发皿蒸发量的主要气象因素分析[J]. 亚热带资源与环境学报, 4(4): 20–29. Li Jingyu, Zhang Zhiguo, Xu Zongxue, et al. 2009. Major meteorological factors affecting pan evaporation in the Tibetan Region[J]. Journal of Subtropical Resources and Environment, 4(4): 20–29. | |
| 刘颖秋. 2002. 黄淮海流域水危机与水资源可持续利用[J]. 科技导报, 20(27): 51–54. Liu Yingqiu. 2002. Water crisis of the Yellow River Valley, the Huaihe River Valley and the Haihe River Valley and sustainable utilization of water resources[J]. SciTechnol Rev, 20(27): 51–54. | |
| 任国玉, 姜彤, 李维京, 等. 2008. 气候变化对中国水资源情势影响综合分析[J]. 水科学进展, 19(6): 772–779. Ren Guoyu, Jiang Tong, Li Weijing, et al. 2008. An integrated assessment of climate change impacts on China's water resources[J]. Adv Water Sci, 19(6): 772–779. | |
| 王青霞, 吕世华, 鲍艳, 等. 2014. 青藏高原不同时间尺度植被变化特征及其与气候因子的关系分析[J]. 高原气象, 33(2): 301–312. DOI:10.7522/j.issn.1000-0534.2014.00002 Wang Qingxia, Lü Shihua, Bao Yan, et al. 2014. Characteristics of vegetation change and its relationship with climate factors in different time-scales on Qinghai-Xizang Plateau[J]. Plateau Meteor, 33(2): 301–312. DOI:10.7522/j.issn.1000-0534.2014.00002 | |
| 张存厚, 吴学宏, 李永利. 2007. 内蒙古近45a蒸发量气候变化特征分析[J]. 干旱区资源与环境, 21(12): 93–98. Zhang Cunhou, Wu Xuehong, Li Yongli. 2007. Characters of the climate change about evaporation in recent 45 years in Inner Mongolia[J]. J Arid Land Resour Environ, 21(12): 93–98. | |
| 张小磊, 杨梅学. 2010. 基于GAME-Tibet IOP的青藏高原蒸散研究[J]. 地理科学, 30(6): 929–935. Zhang Xiaolei, Yang Meixue. 2010. Evapotranspiration in the Tibetan Plateau based on GAME-Tibet IOP data[J]. Scientia Geographica Sinica, 30(6): 929–935. | |
| 张志强, 孙成权. 1999. 全球变化研究十年新进展[J]. 科学通报, 44(5): 464–477. Zhang Zhiqiang, Sun Chengquan. 1999. New progress in global change study[J]. Chinese Sci Bull, 44(5): 464–477. | |
| 朱利, 张万昌. 2005. 基于径流模拟的汉江上游区水资源对气候变化响应的研究[J]. 资源科学, 27(2): 16–22. Zhu Li, Zhang Wanchang. 2005. Responses of water resources to climatic changes in the upper stream of the Hanjiang River Basin based on rainfall-runoff simulations[J]. Resour Sci, 27(2): 16–22. |
2. University of Chinese Academy of Sciences, Beijing 100101, China;
3. Key Laboratory of Tibetan Environment Changes and Land Surface Processes. Chinese Academy of Sciences, Beijing 100101, China;
4. Chinese Academy of Sciences Center for Excellence in Tibetan Plateau Earth Sciences, Beijing 100101, China
 2017, Vol. 36
2017, Vol. 36