2. 中国科学院青藏高原地球科学卓越创新中心, 北京 100101;
3. 中国科学院大学, 北京 100049
湖泊作为陆地水圈的组成部分, 参与局地的水分和能量循环, 特别是大型湖泊对局地强天气过程常常会产生推波助澜的作用(Dutra et al, 2010; Rouse et al, 2008)。湖泊在局地天气和气候系统中的重要地位是由于湖泊水热性质与周围陆面有明显不同, 相对于湖泊周围常被植被覆盖的地表, 湖面具有较低的反照率、较大的比热容和较小的表面粗糙度等。这些差异直接导致了湖泊-大气能量交换与陆地-大气能量交换显著不同, 对感热和潜热通量的分配, 积云和降水的形成(Miles and Verlinde, 2005), 边界层的温湿结构(Schwartz and Karl, 1990)等有显著影响, 并且可能导致中尺度环流的形成(Segal and Arritt, 1992), 进而影响降水的分布(Laird et al, 2009)。因此, 准确模拟湖泊与大气之间的相互作用可以提升对湖区周边天气和气候的理解(刘树华等, 2001)。
青藏高原上面积大于1 km2的湖泊超过1000个, 总面积超过中国湖泊总面积的50%(马荣华等, 2011)。由于青藏高原气候环境恶劣, 观测条件艰苦, 以往对于青藏高原陆气相互作用的研究较多而对湖气相互作用的研究较少。游庆龙等(2007)利用观测台站数据发现纳木错夏季有明显湖陆风现象。李茂善等(2012)利用纳木错湖大气湍流观测资料证实了该湖与周围地表存在明显差异, 导致地表通量分布不均。吕雅琼等(2007)研究发现, 青海湖夏季白天是冷干岛, 且在低空有明显的从湖面向四周辐散的气流, 而夜间是暖湿岛, 且有从北偏东方向来的陆风。Liu et al (2015)利用观测资料发现洱海局地环流明显受到湖陆风和山谷风影响。20世纪90年代, 随着数值模式技术在气象学中日益成熟, 科学家逐渐开始利用数值模式研究青藏高原湖气相互作用。陈万隆等(1995)用一个二维地气耦合模式模拟了青海湖的湖陆风, 湖泊和陆面性质差异对局地中尺度大气环境有重要影响。吕雅琼等(2008)利用MM5模型模拟发现纳木错湖的冷湖效应推迟了边界层湍流混合及对流边界层出现的时间, 边界层高度日变化非常明显, 对流边界层高度最高可达1750 m。王宾宾(2014)利用纳木错小湖的涡动相关资料, 对湖泊传输模型进行了分析和验证, 发现潜热通量受风速影响较大, 风速较小时不稳定大气层结条件下容易发生自由对流, 对水汽能量输送影响很大。Li et al (2009)利用中尺度气象模式WRF模拟纳木错湖的一次降水事件, 发现湖面温度对局地降水有很大影响, 模型模拟的湖表温度存在较大误差。李照国等(2012)利用WRF模式分析了鄂陵湖夏季的湖泊效应, 并用MODIS (Moderate Resolution Imaging Spectroradiometer)湖表温度数据代替模式模拟的湖表温度。结果表明, 夏季晴天中午至傍晚, 鄂陵湖有显著的湖风环流; 白天湖面感热和潜热较小, 昼(夜)表现出明显的冷(暖)湖效应, 湖区低层全天呈现出“湿岛”效应。目前, 科学家将简单的一维湖泊模型耦合进天气模式(Gu et al, 2015; Mironov et al, 2010), 但在青藏高原地区的适用性还有待研究。
近几十年来湖泊模型研究已取得很大进展, 已有的湖泊模型对浅湖的模拟已经成熟, 而深湖和冰湖的模拟效果欠佳(Stepanenko et al, 2010)。除常规物理过程参数化方案外, 湖泊模型还需考虑其自身特有的物理性质, 如盐度(Wen et al, 2015)。从兼顾模拟的物理准确性和计算效率的角度考虑, 一维模型相较于复杂的三维模型更适用于与天气或气候模式的耦合研究, 但究其本身, 仍存在很大的局限性, 例如不能够考虑到湖泊内部的水循环过程。湖泊模型一般是根据少量湖泊观测数据发展而成, 其参数化方案基于物理事实进行了不同程度的简化, 可能适用于特定环境下的湖泊, 其推广应用需要在研究区域进行评估(任晓倩等, 2013)。
本研究的目的是评估WRF (The Weather Research and Forecasting)的湖泊模型(简称WRF-Lake模型)在青藏高原大型湖泊纳木错湖的适用性, 并尝试改进模型。模型驱动数据来自中国科学院青藏高原研究所发展的中国区域高时空分辨率地面气象要素驱动数据集, 模拟结果用湖温观测数据和MODIS湖表温度数据进行验证。
2 研究区域概况和资料选取 2.1 研究区域纳木错湖位于青藏高原中部(30.5°N-30.95°N, 90.2°E-91.05°E, 海拔为4710 m), 湖泊面积2021.3 km2, 是西藏自治区第二大湖泊(Lei et al, 2013)(图 1)。其平均湖深大约为40 m, 最大湖深超过95 m。纳木错湖年降水量超过400 mm, 主要发生在5-10月(Zhou et al, 2013)。

|
图 1 纳木错湖及其周边地形 Figure 1 Location and the topography of Nam Co |
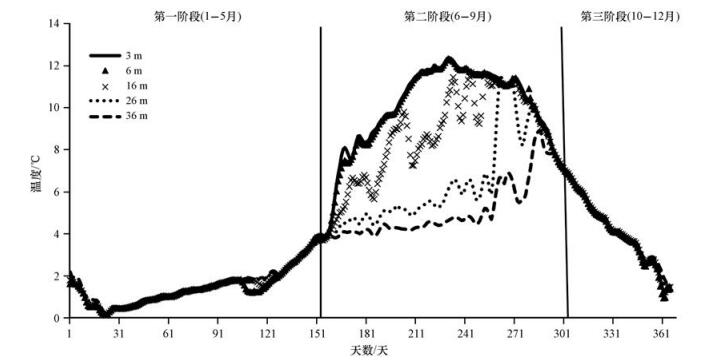
本研究用到两种站点观测数据。第一种是纳木错湖温廓线数据。该数据为2012年日平均湖水温度, 深度分别为3 m, 6 m, 16 m, 26 m和36 m(图 2)。该数据将用于验证模型模拟结果。第二种是纳木错湖岸观测站数据。中国科学院纳木错站始建于2005年, 位于纳木错湖的东南岸, 距离湖边大约2 km。该站提供常规气象要素(气温, 比湿, 气压, 风速风向, 降水和辐射)观测数据。这些观测数据主要用于校正模型驱动数据, 并和湖温数据一起用于波文比法估算纳木错的热通量, 其结果用于验证模拟结果。
|
图 2 2012年观测的纳木错湖5层(3 m, 6 m, 16 m, 26 m和36 m)日平均温度 Figure 2 The observed lake water temperature of Nam Co at five depths (3 m, 6 m, 16 m, 26 m and 36 m) in 2012 |
研究使用的中国区域高时空分辨率地面气象要素驱动数据(何杰, 2010), 是以国际上现有的Princeton再分析资料、GLDAS资料、GEWEX-SRB辐射资料, 以及TRMM降水资料为背景场, 融合了中国气象局常规气象观测数据制作而成。数据时间段从1979年1月1日至2012年12月31日, 时间分辨率为3 h, 空间分辨率0.1°, 包含近地面(2 m)气温、近地面气压、近地面(2 m)空气比湿、近地面(10 m)全风速、地面向下短波辐射、地面向下长波辐射和地面降水率, 共7个变量。该数据可以从以下网址获得: http://westdc.westgis.ac.cn/data/7a35329c-c53f-4267-aa07-e0037d913a21.已有研究表明该数据在中国陆面过程和水文过程研究中良好的表现(Chen et al, 2011; Guo and Wang, 2013; Liu and Xie, 2013)。为了得到更准确的驱动数据, Lazhu et al (2016)根据纳木错站的观测数据对该驱动数据的风场作了修正。本文直接使用修正后的驱动数据。
2.2.3 MODIS卫星数据MODIS地表温度数据产品(MOD11A1) 用于验证湖表温度, 时间跨度从2000至2012年。该数据每天观测2次(11:00和21:00左右, 北京时, 下同), 空间分辨率1 km (Savtchenko et al, 2004; Wan et al, 2004)。很多研究表明MODIS产品有较高的精度(Xiao et al, 2013; Zhang et al, 2014)。已有一些研究利用MODIS数据作为湖泊模型验证数据, 并发现MODIS产品往往比观测到的湖泊混合层温度低(Crosman and Horel, 2009; Reinart and Reinhold, 2008), 这种现象被称作冷表面效应(Robinson et al, 1984; Donlon et al, 2002)。
3 模型介绍本研究所用的湖泊模型是由Gu耦合入WRF的(Gu et al, 2015), 模型最初是由Hostetler et al(1992, 1993)发展而来的。Subin et al (2012)在原模型的基础上在湖泊的底部又添加了10层的土壤层, 在湖泊顶部湖冰上添加了最多5层的雪层, 并对湖冰进行参数化。将其作为陆面过程模型CLM (Community Land Model)的湖泊方案。湖泊内部的能量传送考虑分子扩散和湍流扩散来计算。在该模型中, 分子扩散系数为常数km(1.433×10-7 m·s-1), 近地面的风场和湖水的密度梯度用来参数化计算湍流扩散系数。当湖表温度低于湖水的冻结温度时, 模式中不再考虑湍流扩散的作用。每一层的湖水允许部分冻结, 冻结释放潜热用于加热湖水或湖泊上层的空气。对流混合可以在湖水的任何一层发生, 即使该层的湖水已经冻结。模式中有雪层时没有太阳光进入湖泊, 反之, 则太阳光可以穿透湖水到达湖泊的底部, 到达底部的太阳光则被湖泊底部的第一层土壤层吸收。该模型主要由三部分组成。第一部分由大气的强迫场计算出湖水的表面温度和各种通量(动量通量, 感热通量和水汽通量); 第二部分计算各个垂直层次(20~25层, 包括最多5层雪层, 以及10层湖水和湖底以下10层土壤)的温度; 第三部分考虑湖泊中水的三相变化以及雪的挤压等, 但是没有考虑雪的渗透。预报湖水温度的控制方程是一维热扩散方程:
| $ \frac{{\partial T}}{{\partial t}} = \frac{\partial }{{\partial z}}\left[ {\left( {{k_m} + {k_e}\frac{{\partial T}}{{\partial z}}} \right)} \right] + \frac{1}{{{c_{{\text{liq}}}}}}\frac{{d\emptyset }}{{dz}}, $ | (1) |
式中: T是湖水温度(单位: K), km是分子热扩散系数(单位: m2·s-1), ke是涡旋扩散系数(单位: m2·s-1), cliq是水的体积热容(单位: J·m-3·K-1), Ø是湖深z处吸收的太阳辐射(单位: W·m-2), t是时间, z是湖深(向下为正)。
上边界条件是由表层进入湖泊的热量通量G, 根据能量守恒要求方程可以写成:
| $ G = \left( {1 - \alpha } \right){s_g} + {L_g} - {H_g} - \lambda {E_g}, $ | (2) |
式中: G是进入湖泊的热量通量, (1-α)sg是净短波辐射, Lg是净长波辐射, Hg是向上的感热通量, λEg是向上的潜热通量。
公式(1) 采用Crank-Nicholson方法写成差分形式, 容易整理成三对角矩阵形式的差分方程组, 求解出每一层的温度。垂直涡旋扩散系数采用Hostetler模式的方案。该模式假设湖水在水平方向均一, 热量的分配主要由垂直交换引起。垂直涡旋扩散系数的大小主要由稳定度参数(即理查森数)决定。计算每层的垂直涡旋扩散系数ke, i的参数化方案可以写成如下形式:
| $ {k_{e,{\rm{ }}i}} = \left\{ \begin{array}{l} \frac{{k{w^*}{z_i}}}{{{P_0}(1 + 37R{i^2})}}\exp \left( { - {k^*}{z_i}} \right){\rm{ }},{T_g} > {T_f}\\ 0{\rm{ }},{\rm{ }}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{T_g} \le {T_f} \end{array} \right. $ | (3) |
式中: Ri是理查森数, k=0.4是冯卡曼常数, P0=1为中性层结下的Prandtl数, zi是湖泊各层的深度, Tf是临界冻结温度273.15 K, Tg是湖表温度, w*是表面摩擦速度。
本研究将湖深设为40 m, 为纳木错平均湖深。湖泊总共25层, 湖泊初始温度设为4 ℃, 模拟开始时间为1979年1月1日, 结束时间为2012年12月31日。将3 h分辨率的驱动数据线性插值到10 min分辨率, 并设置时间步长设为10 min。1979年作为模拟预热时间(spin-up)。属于微咸湖, 我们认为盐度的影响很小, 因此在本次研究中我们没有考虑盐度的影响。
4 结果分析 4.1 湖水温度模拟评估与改进根据观测湖温廓线的变化(图 2), 可以将湖泊温度变化分为3个阶段:第一阶段为1-5月, 这一阶段整层湖温低于4 ℃, 太阳辐射穿过冰层加热表层湖水, 使表层湖水密度增大, 产生混合, 故这一阶段整层湖水温度一致。第二阶段是6-9月, 这一阶段湖温大于4 ℃, 太阳辐射由浅到深逐层加热湖水, 整层湖水呈现明显的分层结构。第三阶段是10-12月, 这一阶段由湖水向大气释放热量, 表层湖水冷却下沉, 使整层湖水均匀混合。
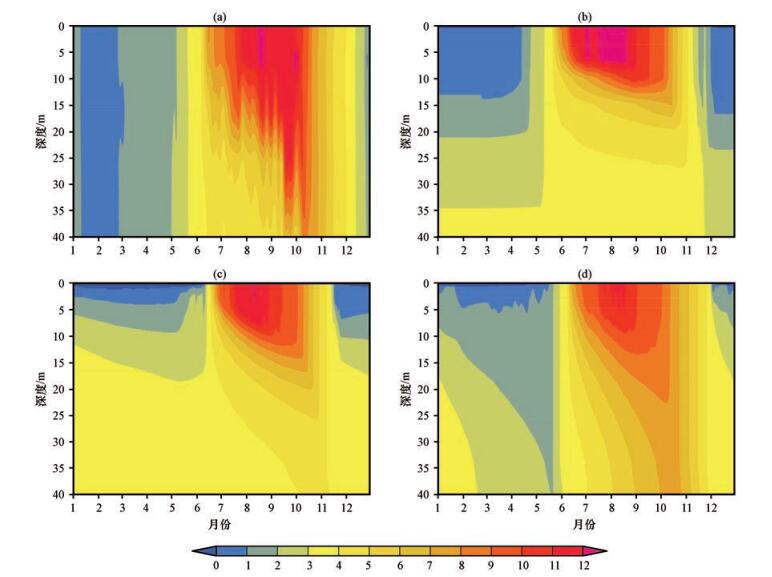
当湖泊深度大于15 m时, WRF湖泊模型会低估湖泊内部热量的传输能力, 原有的湍流扩散系数不足以将湖表能量传输到湖泊内部, 因此需要将ke扩大102~105倍(下称Lake_default方案)(Gu et al, 2015)。由于观测湖水温度廓线难度极大, 只在2012年有较为完整的观测数据, 因此选择2012年作为模拟验证时段。本研究中先采用Lake_default方案模拟2012年全年日平均湖温廓线并与观测资料作对比。结果显示(图 3b)即使扩大ke, 该湖泊模型也不能有效的将湖表能量传递到湖泊深层。能量堆积在15 m以上的湖泊浅层, 导致大量能量迅速释放到大气, 模拟的湖温在冬季迅速下降, 与观测结果(图 3a)相差较大。选择模型中最接近观测深度的数据, 计算均方根误差为3.6 ℃。因此, WRF的湖泊模型方案并不完全适用于纳木错湖。此外, 观测资料显示深层湖水存在着明显的振荡, 表明在湖水内部可能存在增强ke的因素亦或其他形式的混合。
|
图 3 2012年纳木错湖日均温度观测值(a)与Lake_default (b)、Subin (c)、Lake_enhanced (d)方案模拟的全年日平均湖温廓线对比(单位: ℃) Figure 3 Comparison betweenthe observed datas (a) and the simulated lake temperatures by Lake_default (b), Subin (c), Lake_enhanced (d) scheme in 2012.Unit: ℃ |
已有研究指出, 该湖泊模型低估了深湖(>20 m)的湖水混合能力。其原因可能是一维湖泊模型由于自身的局限性, 无法刻画大型湖泊三维流动对湖水混合的影响。这种混合不足会导致湖水浅层在春季升温过快而且秋季降温也过快, 而湖泊底层没有明显的季节变化, 与观测结果相差较大。Fang and Stefan(1996)研究认为:在深湖中存在一些增强湖水混合的机制, 并在ke的基础上引入湍流扩散增强项ked:
| $ {k_{ed}} = 1.{\rm{ }}04 \times {10^{ - 8}}{\left( {{N^2}} \right)^{ - 0.{\rm{ }}43}}, $ | (4) |
式中: N为布伦特维萨拉频率, 表征湖水的密度梯度。
湖水在稳定分层条件下, 湖水密度梯度大, 湍流动能将很快被耗散, 导致扩散能力变小, 反之亦然。通过比较, ked最大可为分子扩散系数km的106倍, ke一般为km的102~103倍, ked在大型湖泊中更为重要。为此, Subin在CLM4.5版本中, 加入了湍流增强项并允许对湍流扩散系数扩大10~100倍。我们按照CLM默认值, 将湍流扩散系数整体扩大10倍(下称Subin方案), 即:
| $ \left( {{k_e} + {k_{ed}}} \right) \times 10, $ | (5) |
结果表明Subin方案相较于Lake_default方案有明显改进, 计算湖温均方根误差为2.0 ℃湖泊浅层能量开始向深层传递, 说明湍流增强项ked能弥补一维模型扩散能力不强的问题, 但传输强度仍然偏小(图 3c)。为改进模拟效果, 本文进一步扩大垂向混合能力。考虑到表层涡旋扩散系数ke的参数化相对成熟, 我们将ked项扩大不同的倍数作敏感性模拟分析(表 1)。由敏感性模拟分析发现当ked扩大100倍时, 模拟与观测的6层湖温之间的均方根误差最小, 为1.16 ℃。该方案(下称Lake_enhanced方案)较原有方案, 湖泊能量传输能力加强, 原方案堆积在浅层的能量能够传递到湖水深层, 也能模拟出湖水向外放热前(10-11月), 整层湖水完全混合的现象(图 3d)。此外, 结冰期模拟效果也较原方案有一定改进, 模拟的融冰期和冻结期都与观测结果接近, 但冻结期深层湖水温度为4 ℃, 说明模拟的深层湖水并没有接收到外界能量或者发生垂向混合, 而观测数据显示冻结期整层湖水混合均匀。所以整个冻结期的模拟还有待改进。
| 表 1 湍流增强项ked扩大敏感性分析 Table 1 Sensitivity analysis of enhanced diffusion ked |
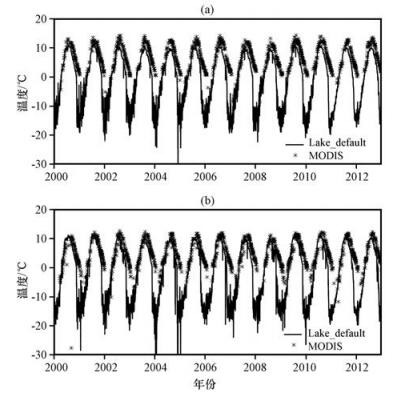
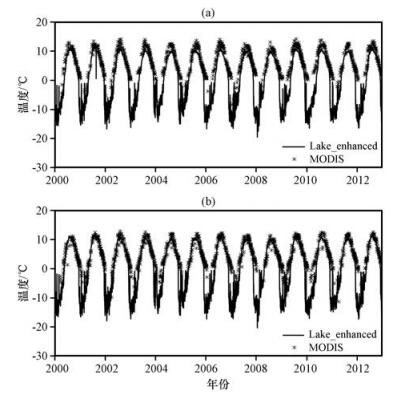
本研究利用MODIS湖表温度数据验证模拟结果。MODIS卫星在纳木错湖过境时间分别是白天(约11:00) 和晚上(约21:00), 时间跨度2000-2012年。对模拟结果的验证也选择相应时间。MODIS产品经过质量控制后可用数据主要出现在湖水未冻结期(5-12月), 这可能是因为在冻结期MODIS不能区分云和湖冰及湖冰上积雪。MODIS湖表温度观测与Lake_default方案湖表温度模拟的对比(图 4)显示, 在未冻结期, Lake_default方案湖表温度模拟结果与MODIS相比, 白天和晚上均方根误差分别是8.0 ℃和7.9 ℃。湖水升温阶段模拟较为准确, 但随后湖表温度迅速下降, 与MODIS数据相差较大, 原因可能是大量能量聚集在湖水浅层以热通量的形式释放到大气, 导致湖水内部能量不足, 在湖水降温时期温度迅速降低。增强ked(Lake_enhanced方案)后, 总体结果明显好于Lake_default方案(图 5)。模拟的白天和晚上湖表温度的均方根误差分别为2.58 ℃和1.38 ℃, 晚上的模拟结果总是好于白天。湖水升温阶段和降温阶段模拟效果好。但湖表温度达到最高的时期, 模拟的湖温略微偏低。综上所述, Lake_enhanced方案模拟结果较之Lake_default方案能更好的模拟出湖表温度, 但模拟湖水有提前结冰的现象, 仍需进一步改进。
|
图 4 2000-2012年MODIS湖表温度与Lake_default方案模拟结果对比(单位: ℃) (a) 09:00, (b) 21:00 Figure 4 Comparison of daily lake surface temperature of Nam Co between the MODIS observation and the Lake default simulation during 2000-2012.Unit: ℃ |
|
图 5 2000-2012年MODIS湖表温度与Lake_enhanced方案模拟结果对比(单位: ℃) (a) 09:00, (b) 21:00 Figure 5 Comparison of daily lake surface temperature of Nam Co between the MODIS observation and the Lake enhanced simulation during 2000-2012.Unit: ℃ |
为了佐证湖泊模型降温过快的现象是由于大量能量聚集在浅层以热通量形式释放到大气, 本研究对模拟和观测数据进行湖表能量平衡分析。湖表能量平衡方程为:
| $ {R_{{\rm{net}}}} = H + LE + G, $ | (6) |
式中: Rnet为净辐射, LE为潜热通量, H为感热通量, G为湖泊储热量。
净辐射包括短波净辐射和长波净辐射, 净短波辐射取决于湖表反照率(水面约0.07, 冰面约0.6), 净长波辐射取决于湖表温度。湖泊储热量由2012年湖温观测数据计算, 公式如下:
| $ G = \int {\rho \times C \times \frac{{{\rm{d}}\theta }}{{{\rm{d}}t}}{\rm{d}}z} , $ | (7) |
式中: ρ是水的密度(单位: kg·m-3), C水的比热容(单位: J·kg-1·℃-1), θ是在深度z(m)的湖水温度(单位: ℃), t是时间(单位:天)。
潜热通量和感热通量并没有观测数据, 利用纳木错站气象数据和湖面温度根据波文比推算得到。波文比定义为感热通量与潜热通量的比值, 公式如下:
| $ R = \frac{H}{{lE}} = \frac{{{C_p}P}}{{\varepsilon L}}\frac{{{T_0} - {T_{\rm{a}}}}}{{{e_0} - {e_{\rm{a}}}}}, $ | (8) |
式中: Cp=1004 J·kg-1·K-1, L=2.56×106 J·kg-1, ε=0.622, P(Pa)为气压, T0为湖表温度(单位: ℃), Ta为空气温度(单位: ℃), e0为饱和水汽压(单位: Pa), ea为水汽压(单位: Pa)。
图 6为2012年三个阶段模型改进前后与观测数据比较的结果。波文比推导的感热通量在三个阶段逐渐增大, 第三阶段达到最大, 为66.0 W·m-2。两种方案在趋势上与波文比推导的结果一致, 但Lake_enhanced方案较之Lake_default方案误差小。潜热通量与感热通量的季节变化一致, 但每个阶段都比感热大, 第三阶段达到最大值119.2 W·m-2。Lake_default方案对潜热通量趋势模拟有误, 在第二阶段达到最大值105.3 W·m-2, 比波文比推导结果(52.1 W·m-2)大一倍。Lake_enhanced方案有效地改进了潜热模拟, 全年趋势与观测一致, 且误差较小。湖泊储热量在前两个阶段为正值表示湖泊从外界吸收热量, 最后一个阶段为负值表示湖泊向外界放热。两个方案都能模拟出这种趋势, 但Lake_default的方案存在较大误差, 在第二阶段没有储存足够的热量, 导致第三阶段释放热量也较小。Lake_enhanced方案对模型的改进效果明显, 与观测接近。
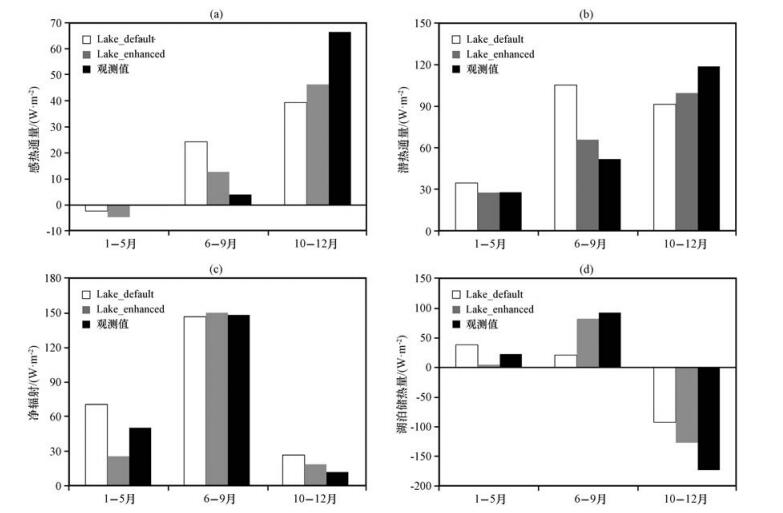
|
图 6 2012年观测数据及Lake_default方案, Lake_enhanced方案模拟的湖表能量平衡结果分析(单位: W·m-2) (a)感热通量, (b)潜热通量, (c)净辐射, (d)湖泊储热量 Figure 6 Comparison of the lake surface energy between the Bowen ratio-derived (observed) and the WRF-simulated for the three periods (P1-P3) of 2012.Unit: W·m-2. (a) sensible heat fluxes, (b) latent heat fluxes, (c) net radiation, (d) increment of heat storage in water |
通过湖表能量平衡分析, 验证了之前的推理: Lake_default案由于模拟的湖表温度过高, 导致热量通量在夏秋季过大, 大量能量释放到大气, 湖泊储热量不足, 这与观测结果存在较大误差。通过提高湖泊内部的混合能力, 新方案Lake_enhanced能够储存更多能量到湖泊深部, 与观测更接近, 从而改进了湖表能量平衡的季节变化模拟。新方案在湖水冻结期有一定改进, 但仍存在不小误差, 需要进一步讨论。
5 结论利用卫星观测资料和站点资料, 在西藏的大型深水湖泊纳木错评估了WRF3.6.1(2014年发布)版本新耦合的湖泊模型在模拟湖水温度和湖表能量平衡方面的性能。得到以下主要结论:
(1) 该模型在纳木错湖模拟效果并不理想, 主要表现为湖水混合能力不够, 湖泊深部没有加热, 大量热量聚集在湖水浅层并以热通量的形式过早释放到大气, 导致湖泊秋季提前降温。这是由于大型深湖的三维流动可以强化湖水的混合, 而在目前一维模型中无法参数化所致。
(2) 通过在模式中扩大混合系数, 增强湖水混合能力, 能够有效改进原模型的不足, 使得能量在夏季可以储存在湖泊内部, 这与观测事实相符。改进后的模型可以准确模拟未冻结期湖水温度和能量分配。
(3) 对于冻结期湖温模拟, 模拟结果还不够准确, 其原因是水体相变过程对湖泊能量平湖的影响在模式中存在不足之处, 将在今后能研究中进一步改进。
| Chen Y, Yang K, He J, et al. 2011. Improving land surface temperature modeling for dry land ofChina[J]. J Geophys Res, 116(D20): D20104. DOI:10.1029/2011JD015921 | |
| Crosman E T, Horel J D. 2009. MODIS-derived surface temperature of the Great Salt Lake[J]. Remote Sens Environ, 113(1): 73–81. DOI:10.1016/j.rse.2008.08.013 | |
| Donlon C, Minnett P, Gentemann C, et al. 2002. Toward improved validation of satellite sea surface skin temperature measurements for climate research[J]. J Climate, 15: 353–369. DOI:10.1175/1520-0442(2002)015<0353:TIVOSS>2.0.CO;2 | |
| Dutra E, Stepanenko V M, Balsamo G, et al. 2010. An offline study of the impact of lakes on the performance of the ECMWF surface scheme[J]. Boreal Environ Res, 15: 100–112. | |
| Fang X, Stefan H G. 1996. Long-term lake water temperature and ice cover simulations measurements[J]. Cold Reg Sci Technol, 24: 289–304. DOI:10.1016/0165-232X(95)00019-8 | |
| Gu H, Jin J, Wu Y, et al. 2015. Calibration and validation of lake surface temperature simulations with the coupled WRF-lake model[J]. Climatic Change, 129(3-4): 471–483. DOI:10.1007/s10584-013-0978-y | |
| Guo D, Wang H. 2013. Simulation of permafrost and seasonally frozen ground conditions on the Tibetan Plateau, 1981-2010[J]. J Geophys Res Atmos, 118: 5216–5230. DOI:10.1002/jgrd.50457 | |
| Hostetler S W, Giorgi F. 1992. Use of a regional atmospheric model to simulate lake-atmosphere feedbacks associated with Pleistocene Lakes Lahontan and Bonneville[J]. Climate Dyn, 7: 39–44. | |
| Hostetler S W, Bates G T, Giorgi F. 1993. Interactive coupling of a lake thermal model with a regional climate model[J]. J Geophys Res, 98: 5045. DOI:10.1029/92JD02843 | |
| Lazhu, Yang K, Lei Y, et al. 2016. Quantifying evaporation and its decadal change for Lake Nam Co, central Tibetan Plateau[J]. J Geophys Res:Atmospheres, 121(13): 7578–7591. DOI:10.1002/jgrd.v121.13 | |
| Laird N F, Desrochers J, Payer M. 2009. Climatology of lake-effect precipitation events over Lake Champlain[J]. J Appl Meteorol Climatol, 48(2): 232–250. DOI:10.1175/2008JAMC1923.1 | |
| Lei Y, Yao T, Bird B W, et al. 2013. Coherent lake growth on the central Tibetan Plateau since the 1970s:Characterization and attribution[J]. J Hydrol, 483: 61–67. DOI:10.1016/j.jhydrol.2013.01.003 | |
| Li M, Ma Y M, Hu Z, et al. 2009. Snow distribution over the Namco lake area of the Tibetan Plateau[J]. Hydrol Earth Syst Sci, 13: 2023–2030. DOI:10.5194/hess-13-2023-2009 | |
| Liu H Z, Feng J W, Sun J H, et al. 2015. Eddy covariance measurements of water vapor and CO2 fluxes above the Erhai Lake[J]. Science China Earth Science, 3: 317–328. | |
| Liu J G, Xie Z H. 2013. Improving simulation of soil moisture in China using a multiple meteorological forcing ensemble approach[J]. Hydrology and Earth System Sciences, 17(9): 3355–3369. DOI:10.5194/hess-17-3355-2013 | |
| Miles N L, Verlinde J. 2005. Observations of Transient Linear Organization and Nonlinear Scale Interactions in Lake-Effect Clouds.Part Ⅰ:Transient Linear Organization[J]. Mon Wea Rev, 133: 667–691. | |
| Mironov D, Heise E, Kourzeneva E, et al. 2010. Implementation of the lake parameterisation saheme FLake into the numerical weather prediction model COSMO[J]. Boreal environment research, 15(2): 218–230. | |
| Reinart A, Reinhold M. 2008. Mapping surface temperature in large lakes with MODIS data[J]. Remote Sens Environ, 112: 603–611. DOI:10.1016/j.rse.2007.05.015 | |
| Robinson I, N Wells, Charnock H. 1984. The sea surface thermal boundary layer and its relevance to the measurement of sea surface temperature by airborne and spaceborne radiometers[J]. Int J Remote Sens, 5: 19–45. DOI:10.1080/01431168408948787 | |
| Rouse W R, Blanken P D, Bussières N, et al. 2008. An Investigation of the Thermal and Energy Balance Regimes of Great Slave and Great Bear Lakes[J]. J Hydrometeorol, 9: 1318–1333. DOI:10.1175/2008JHM977.1 | |
| Savtchenko A, Ouzounov D, Ahmad S, et al. 2004. Terra and Aqua MODIS products available from NASA GES DAAC[J]. Adv Space Res, 34: 710–714. DOI:10.1016/j.asr.2004.03.012 | |
| Schwartz M D, Karl T R. 1990. Spring Phenology:Nature's Experiment to Detect the Effect of "Green-Up" on Surface Maximum Temperatures[J]. Mon Weather Rev, 118(4): 883–890. DOI:10.1175/1520-0493(1990)118<0883:SPNETD>2.0.CO;2 | |
| Segal M, Arritt R W. 1992. Nonclassical mesoscale circulations caused by surface sensible heat-flux gradients[J]. Bull Amer Meteor Soc, 73(10): 1593–1604. DOI:10.1175/1520-0477(1992)073<1593:NMCCBS>2.0.CO;2 | |
| Stepanenko V M, Goyette S, Martynov A, et al. 2010. First steps of a Lake Model intercomparison project:LakeMIP[J]. Boreal Environ Res, 15(2): 191–202. | |
| Subin Z M, Riley W J, Mironov D. 2012. An improved lake model for climate simulations:model structure, evaluation, and sensitivity analyses in CESM1[J]. Journal of Advances in Modeling Earth Systems, 4: 1–27. | |
| Wan Z, Zhang Y, Zhang Q, et al. 2004. Quality assessment and validation of the MODIS global land surface temperature[J]. Int J Remote Sens, 25: 261–274. DOI:10.1080/0143116031000116417 | |
| Wen L J, Nagahatla N, Zhao L, et al. 2015. Impacts of salinity parameterizations on temperature simulation over and in a hypersaline lake[J]. Chinese Journal of Oceanology and Limnology, 3: 790–801. | |
| Xiao F, Ling F, Du Y, et al. 2013. Evaluation of spatial-temporal dynamics in surface water temperature of Qinghai Lake from 2001 to 2010 by using MODIS data[J]. J Arid Land, 5: 452–464. DOI:10.1007/s40333-013-0188-5 | |
| Zhang G, Yao T, Xie H, et al. 2014. Estimating surface temperature changes of lakes in the Tibetan Plateau using MODIS LST data[J]. J Geophys Res Atmos, 119: 8552–8567. | |
| Zhou S, Kang S, Chen F, et al. 2013. Water balance observations reveal significant subsurface water seepage from Lake Nam Co, south-central Tibetan Plateau[J]. J Hydrol, 491: 89–99. DOI:10.1016/j.jhydrol.2013.03.030 | |
| 陈万隆, 孙卫国, 周竞南, 等. 1995. 青海湖湖陆风的数值研究[J]. 湖泊科学, 7(4): 289–296. DOI:10.18307/1995.0401Chen Wanlong, Sun Weiguo, Zhou Jingnan, et al. 1995. A numerical simulation on lake-land breeze of Qinghai Lake[J]. Lake Sci, 7(4): 289–296. DOI:10.18307/1995.0401 | |
| 何杰. 2010. 中国区域高时空分辨率气象要素数据集的建立[D]. 北京: 中国科学院大学, 1-77. He Jie.2010.Development of a surface meteorological dataset of China with high temporal and spatial resolution[D].Beijing:University of Chinese Academy of Sciences, 1-77. | |
| 李茂善, 杨耀先, 马耀明, 等. 2012. 纳木错(湖)地区湍流数据质量控制和湍流通量变化特征[J]. 高原气象, 31(4): 875–884. Li Maoshan, Yang Yaoxian, Ma yaoming, et al. 2012. Analyses on turbulence data control dan distribution of surface energy flux in Namco area of Tibetan Plateau[J]. Plateau Meteor, 31(4): 875–884. | |
| 李照国, 吕世华, 奥银焕, 等. 2012. 黄河源区生态环境变化对湖泊效应影响的数值模拟[J]. 高原气象, 31(6): 1591–1600. Li Zhaoguo, Lu Shihua, Ao Yinhuan, et al. 2012. Numerical simulation of impact of ecological environment change on lake effect in the source region of the Yellow River[J]. Plateau Meteor, 31(6): 1591–1600. | |
| 刘树华, 文平辉, 张云雁, 等. 2001. 陆面过程和大气边界层相互作用敏感性实验[J]. 气象学报, 59(5): 533–548. DOI:10.11676/qxxb2001.058Liu Shuhua, Wen Pinghui, Zhang Yunyan, et al. 2001. Sensitivity tests of interaction between land surface physical process and atmospheric boundary layer[J]. Acta Meteor Sinica, 59(5): 533–548. DOI:10.11676/qxxb2001.058 | |
| 吕雅琼, 杨显玉, 马耀明. 2007. 夏季青海湖局地环流及大气边界层特征的数值模拟[J]. 高原气象, 24(4): 686–692. Lü Yangqiong, Yang Xianyu, Ma Yaoming. 2007. Numerical simulation of summer circulation atmospheric boundary layer characteristics over Qinghai Lake[J]. Plateau Meteor, 24(4): 686–692. | |
| 吕雅琼, 马耀明, 李茂善, 等. 2008. 青藏高原纳木错湖区大气边界层结构分析[J]. 高原气象, 27(6): 1205–1210. Lü Yaqiong, Ma Yaoming, Li maoshan, et al. 2008. Study on characteristic of atmospheric boundary layer over lake Namco region, Tibetan Plateau[J]. Plateau Meteor, 27(6): 1205–1210. | |
| 马荣华, 杨桂山, 段洪涛, 等. 2011. 中国湖泊的数量、面积与空间分布[J]. 中国科学:地球科学, 41(3): 394–401. Ma Ronghua, Yang Guishan, Duan Hongtao, et al. 2011. China's lakes at present:Number, area and spatial distribution[J]. Science in China:Earth Sci, 41(3): 394–401. | |
| 任晓倩, 孙菽芬, 陈文, 等. 2013. 湖泊数值模拟研究现状综述[J]. 地球科学进展, 28(3): 347–356. DOI:10.11867/j.issn.1001-8166.2013.03.0347Ren Xiaoqian, Sun Shufen, Chen Wen, et al. 2013. A review of researches on the lake numerical modeling[J]. Adv Earth Sci, 28(3): 347–356. DOI:10.11867/j.issn.1001-8166.2013.03.0347 | |
| 王宾宾. 2014. 利用MODIS资料估算青藏高原感热和潜热通量的时空分布及变化[D]. 北京: 中国科学院大学, 1-127. Wan Binbin.2014.The spatial distribution and temporal variation of sensible and latent heat flux on the Tibetan Plateau by using MODIS data[D].Beijing:University of Chinese Academy of Sciences, 1-127. | |
| 游庆龙, 康世昌, 李潮流, 等. 2007. 青藏高原纳木错气象要素变化特征[J]. 气象, 33(3): 54–60. DOI:10.7519/j.issn.1000-0526.2007.03.008You Qinglong, Kang Shichang, Li Chaoliu, et al. 2007. Variation features of meteorological elements at Namco station, Tibetan Plateau[J]. Plateau Meteor, 33(3): 54–60. DOI:10.7519/j.issn.1000-0526.2007.03.008 |
2. Center for Excellence in Tibetan Plateau Earth Sciences, Chinese Academy of Sciences, Beijing 100101, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
 2017, Vol. 36
2017, Vol. 36
