在资料同化中, 由于非线性系统的集合卡尔曼滤波(Ensemble Kalman Filter, EnKF)(Evensen, 2003)方法对模型误差的忽略及初始背景条件的不确定, 导致对协方差矩阵的估计不准确(Whitaker and Hamill, 2002), 通常会降低滤波性能, 甚至会造成滤波发散。针对这类问题, Anderson et al (1999)、Jaison and Youmin (2009)、Bocquet and Sakov (2012)提出了协方差放大法, Hamill(2001)、Sakov and Bertino (2011)提出了解决背景误差虚假相关问题的局地化方法。协方差放大法的原理是利用放大因子缓解协方差被低估的现象。目前, 放大因子的选择都是经验性的, 这种方式会打破系统的物理平衡, 不能消除虚假相关问题。邱晓滨和邱崇践(2009)提出了一种混合误差协方差的方法。混合误差协方差的方法是将定常或准定常的高斯型预报误差协方差和由预报集合估计的预报误差协方差加权平均用于集合卡尔曼滤波同化, 实验发现在混合了依流型而变的预报误差协方差矩阵时, 同化效果得到明显的提高。邵爱梅等(2011)对Qiu et al(2007)基于集合的4DVar方法做了改进得出混合样本方法可以提高同化效果。随后相关学者将BP神经网络应用到资料同化领域来提高同化效果(刘亚亚等, 2010; 胡春梅等, 2010; 李虎超等, 2015)。Luo and Hoteit(2013, 2014)提出残差逼近法, 其原理是在状态变量估计时, 利用残差协方差放大方法, 使放大因子在一个确定的范围内。然而, 无论是适用于线性系统的卡尔曼滤波(Kalman Filter, KF)方法, 还是适用于非线性系统的EnKF方法, 资料同化的优良性都是建立在系统的动态模型准确且噪声的统计特性为已知白噪声的基础之上。但是, 在实际的大气问题中, 很多误差的统计特性不满足零均值高斯分布的假设条件, 或者统计特性未知。因此, 需要进一步研究普适意义上的同化方法。
鲁棒滤波是将鲁棒控制设计中的性能指标H∞范数应用于滤波, 以解决系统中存在的各种不确定性问题(Luo and Hoteit, 2011), 也被称作H∞滤波(H-infinity filter, HF)(Simon, 2006)。Wang and Cai (2008)对HF和KF进行了比较研究, 结果表明: HF和KF的不同之处在于它用未知的具有有限能量的确定性干扰代替白噪声过程驱动状态空间系统, 同时保证从干扰到估计误差的能量增益小于预选确定的正数, 不需要对其统计特性做相应的假设。为了应用于顺序资料同化和解决高维资料同化系统问题, Luo and Hoteit (2011)将集合的思想应用于时间局地化的H∞滤波(Time-Local H-infinity Filter, TLHF)。Altaf et al (2013)利用鲁棒自适应放大法改进集合卡尔曼预报的准确性。Triantafyllou et al (2013)将基于集合的鲁棒卡尔曼滤波应用到生态资料同化中, 提高了滤波的精度及鲁棒性。
文中针对资料同化中误差协方差矩阵低估问题, 提出了一种具有鲁棒稳健性的基于集合时间局地化的H∞滤波(Ensemble Time-Local H-infinity Filter, EnTLHF)资料同化新方法。通过利用分析误差协方差矩阵的逆阵为半正定的条件, 放大转移矩阵的特征值, 从而间接地放大分析误差协方差矩阵, 避免了直接对分析误差协方差矩阵进行复杂的奇异值分解(Singular Value Decomposition, SVD)(Luo and Hoteit, 2011), 降低了大尺度问题中的计算强度。
本文首先介绍了集合转换卡尔曼滤波(Ensemble Transform Kalman Filter, ETKF) (Petersen et al, 2007; Bishop et al, 2001)、TLHF及一种放大转移矩阵特征值的新同化方法; 然后利用Lorenz-96混沌系统进行了数值实验, 考察了EnTLHF在不同的初始背景及不同模型误差条件下的鲁棒性; 最后分析了放大转移矩阵新同化方案, 在不同性能水平系数下的鲁棒稳健性。实验结果表明, 该方法对不同的初始背景, 不同模型误差及不同的性能水平系数具有较好的鲁棒稳健性。
2 资料同化方法离散时间上的预报方程和观测方程分别表示为:
| $ {x_i} = {M_{i,i - 1}}\left( {{x_{i - 1}}} \right) + {u_i}, $ | (1) |
| $ {y_i} = {H_i}\left( {{x_i}} \right) + {v_i}, $ | (2) |
式中: xi∈Rm是第i时刻m维的状态变量; yi∈Rp是p维的观测向量; 转移算子Mi, i-1: Rm→Rm映射xi-1→xi; 观测算子Hi: Rm→Rp从状态空间变换到观测空间; ui和vi分别是预报误差向量和观测误差向量。
2. 1 集合转换卡尔曼滤波(ETKF)(1) 计算第i时刻的预报值及预报协方差矩阵
| $ x_{i,j}^b = {M_{i,i - 1}}\left( {x_{i - 1,j}^a} \right), $ | (3) |
| $ \bar x_i^b = \frac{1}{n}\sum\limits_{j = 1}^n {x_{i,j}^b} , $ | (4) |
| $ X_i^b = \frac{1}{{\sqrt {n - 1} }}\left[ {x_{i,1}^b - \bar x_i^b, \cdots ,x_{i,n}^b - \bar x_i^b} \right], $ | (5) |
| $ P_i^b = X_i^b{\left( {X_i^b} \right)^T}, $ | (6) |
式中: xi-1, ja是i-1时刻的第j个分析值(j=1, …, n), n为集合数的大小, xib是i时刻集合的均值, Xib是预报误差协方差矩阵Pib的平方根。
(2) 计算第i时刻的分析值及分析协方差矩阵
| $ {K_i} = P_i^bH_i^T{\left( {{H_i}P_i^bH_i^T + {R_i}} \right)^{ - 1}}, $ | (7) |
| $ \bar x_i^a = \bar x_i^b + {K_i}\left( {{y_i} - {H_i}\bar x_i^b} \right), $ | (8) |
| $ X_i^a = X_i^b{T_i}{U_i}, $ | (9) |
| $ P_i^a = X_i^a{\left( {X_i^a} \right)^T}, $ | (10) |
式中: Ki是卡尔曼增益, T表示转移矩阵(Wang et al, 2004), T=C(Γ+1)-0. 5, C, Γ分别表示(HXb)TR-1HXb的特征向量和特征值, T*T′的特征值是(Γ+1)-1, H是观测算子, R是观测误差协方差矩阵, U是调整酉矩阵(unitiary matrix)(Julier, 2003)。
| $ x_{i,j}^a = \bar x_i^a + \sqrt {n - 1} {\left( {X_i^a} \right)_j}, $ | (11) |
式中: xia是i时刻的分析均值, Xia是分析误差协方差矩阵Pia的平方根, xi, ja是i时刻第j个分析值。
2. 2 时间局地化的H∞滤波(TLHF)HF(Simon, 2006)是鲁棒滤波的一种, 其解不需要对模型和观测误差作任何的假设。无论模型误差和观测误差的大小, 只要HF范数小于预先设定的正值
为了满足顺序资料同化, Luo and Hoteit(2011)提出比原始滤波HF更加灵活的TLHF。TLHF的目标函数为:
| $ J_{x,i}^{HF} = \frac{{\left\| {{x_i} - x_i^a} \right\|_{{S_i}}^2}}{{\left\| {{x_i} - x_i^b} \right\|_{{{\left( {\Delta _i^b} \right)}^{ - 1}}}^2 + \left\| {{u_i}} \right\|_{Q_i^{ - 1}}^2 + \left\| {{v_i}} \right\|_{R_i^{ - 1}}^2}}, $ | (12) |
| $ \left\| {{x_i} - x_i^a} \right\|_{{S_i}}^2 \le \frac{1}{{{\gamma _i}}}\left( {\left\| {{x_i} - x_i^b} \right\|_{{{\left( {\Delta _i^b} \right)}^{ - 1}}}^2 + \left\| {{u_i}} \right\|_{Q_i^{ - 1}}^2 + \left\| {{v_i}} \right\|_{R_i^{ - 1}}^2} \right), $ | (13) |
式中: xi是系统的真值, xia是xi的估计值, Si是半正定的权重矩阵, 由设计者自由选择, xib是xi的预报值, Δib是相对应的背景协方差矩阵, γi是第i次循环的局地化性能水平, 满足式(14)。
| $ \frac{1}{{{\gamma _i}}} > \frac{1}{{\gamma _i^ * }} \equiv \mathop {\inf }\limits_{x_i^a} \mathop {\sup }\limits_{{x_i},{u_i},{v_i}} J_{x,i}^{HF}, $ | (14) |
式(14) 是最小最大准则, 其中inf是下界(以xia为变量), sup是上界(以xi, μi, vi为变量)。
TLHF的滤波过程如下:
预报:
| $ x_i^b = {M_{i,i - 1}}x_{i - 1}^a, $ | (15) |
| $ \Delta _i^b = {M_{i,i - 1}}\Delta _{i - 1}^aM_{i,i - 1}^T + {Q_i}, $ | (16) |
滤波:
| $ x_i^a = x_i^b + {G_i}\left( {{y_i} - {H_i}x_i^b} \right), $ | (17) |
| $ {\left( {\Delta _i^a} \right)^{ - 1}} = {\left( {\Delta _i^b} \right)^{ - 1}} + {\left( {{H_i}} \right)^T}{\left( {{R_i}} \right)^{ - 1}}{H_i} - {\gamma _i}{S_i}, $ | (18) |
| $ {G_i} = \Delta _i^a{\left( {{H_i}} \right)^T}{\left( {{R_i}} \right)^{ - 1}}, $ | (19) |
式中: Δib是预报误差协方差矩阵, Δia是分析误差协方差矩阵, Gi是增益矩阵。
目标限制:
| $ {\left( {\Delta _i^a} \right)^{ - 1}} = {\left( {\Delta _i^b} \right)^{ - 1}} + {\left( {{H_i}} \right)^T}{\left( {{R_i}} \right)^{ - 1}}{H_i} - {\gamma _i}{S_i} \ge 0. $ | (20) |
式(18) 中的(Δib)-1+(Hi)T(Ri)-1Hi与KF中的分析误差协方差矩阵的逆阵相等(Luo and Hoteit, 2011)。因此, TLHF与KF主要的区别是:分析误差协方差矩阵的逆阵中多出γiSi。当γi=0时, TLHF与KF相同, 即KF可以看成是TLHF的一种特殊形式。
2.3 集合时间局地化的H∞滤波(EnTLHF)由以上分析可知, 当γi=0时, 式(13) 中估计误差能量小于无穷, 即集合滤波算法在同化时并不能保证估计误差的能量有界, 该算法对误差不具备鲁棒性; 而TLHF方法在系统受到一定扰动影响时, 能保证估计误差的能量最小, 说明TLHF算法对扰动变化表现出较好的鲁棒稳健性, 但对于高度非线性的系统滤波精度不高。因此, 将集合的思想应用于TLHF方法, 形成集合滤波的鲁棒框架。其基本原理是利用式(17), (18), (19) 更新背景集合到分析集合, 并根据分析集合计算系统状态的统计特性(均值和协方差), 然后向前演进分析集合, 计算下一步同化循环的背景集合, 依次类推。对于式(18), 当γi>0时, -γiSi<0, 因此估计协方差矩阵大于γi=0时的协方差值, 即额外项-γiSi放大了估计协方差矩阵。理论上, EnTLHF为协方差放大提供了基于鲁棒控制理论的数学机理, 下面列举了EnTLHF的几种特殊形式, 建立了与已存在的协方差放大的集合卡尔曼滤波的联系, 具有如下情形:
当γiSi=α(Pib)-1时:
| $ {\left( {\Delta _i^a} \right)^{ - 1}} = \left( {1 - \alpha } \right){\left( {P_i^b} \right)^{ - 1}} + {\left( {{H_i}} \right)^T}{\left( {{R_i}} \right)^{ - 1}}{H_i}, $ | (21) |
式中: α是性能水平系数。这种放大形式称为背景协方差放大。
当γiSi=α[(Δib)-1+(Hi)T(Ri)-1Hi]=α(Pia)-1时:
| $ {\left( {\Delta _i^a} \right)^{ - 1}} = \left( {1 - \alpha } \right){\left( {P_i^a} \right)^{ - 1}}, $ | (22) |
这种条件下的放大称为分析协方差放大。
当Si=Im时:
| $ {\left( {\Delta _i^a} \right)^{ - 1}} = {\left( {X_i^b{C_i}} \right)^{ - T}}\left( {{\mathit{\Gamma }_i} + I} \right){\left( {X_i^b{C_i}} \right)^{ - 1}} - {\gamma _i}{I_m}. $ | (23) |
在EnTLHF中, Γ=diag(σi, 1, σi, 2, …, σi, n-1)是包含特征值σi, j的对角阵, 当j<l时, σi, j≤σi, l, 为了满足(Δia)-1≥0, 即σi, j-(γi-1)≥0, 方便起见, 令γi-1=ασi, n-1, α∈[0, 1), 在这些条件下得到:
| $ \begin{array}{l} {\left( {\Delta _i^a} \right)^{ - 1}} = {\left( {X_i^b{C_i}} \right)^{ - T}}\left( {{\mathit{\Gamma }_i} - \alpha {\sigma _{i,n - 1}}{I_m}} \right){\left( {X_i^b{C_i}} \right)^{ - 1}}\\ \;\;\;\;\;\;\;\;\;\; = {\left( {X_i^b{C_i}} \right)^{ - T}}{\rm{diag}}\left( {{\sigma _{i,1}} - \alpha {\sigma _{i,n - 1}}, \cdots ,} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\left( {1 - \alpha } \right){\sigma _{i,n - 1}}} \right){\left( {X_i^b{C_i}} \right)^{ - 1}}. \end{array} $ | (24) |
这种形式的放大定义为转移矩阵放大, 其本质是放大转移矩阵的特征值。其放大机理类似于Luo and Hoteit(2011), 基本原理是:首先对分析协方差矩阵进行SVD分解, 然后对其特征值ηi, j(j=1, …, m)进行放大处理, 即用
在一般的协方差放大理论中, 放大因子在同化的过程中保持不变, 而在EnTLHF中, γi=ασi, n-1+1在时间上不仅是自适应的(随着i变化), 而且对系统的每种模式都不相同(XibCi的列不同)。其他自适应的放大方法可以参考Miyoshi et al (2011)和Hoteit et al (2002)的文献。
3 数值实验 3.1 Lorenz-96高维混沌系统Lorenz-96系统(Lorenz and Emanuel, 1998)是一个由微分方程主导的二阶非线性动力系统, 即:
| $ \frac{{{\rm{d}}{X_k}}}{{{\rm{d}}t}} = \left( {{X_{k + 1}} - {X_{k - 2}}} \right){X_{k - 1}} - {X_k} + F, $ | (25) |
式中: k=1, 2, …, 40, X-1=X39, X0=X40, X1=X41。式(25) 是通过气象主导方程的简化所得, 其右边三项分别认为是非线性平流项、阻尼项和外部强迫性。强迫项F=8, 但在同化方法研究中可以通过改变强迫项值, 来代表不同程度的模型误差, 检验同化方法的鲁棒性。
利用经典四阶Runge-Kutta公式可以获得式(25) 的数值解, 迭代总步长为2000步。为了避免暂态影响, 舍去前500步进行同化实验, 取无量纲单位的时间间隔为0. 05。
3.2 观测系统观测系统的观测公式为:
| $ {y_i} = H\left( {{x_i}} \right) + {v_i}, $ | (26) |
式中:状态向量xi在i时刻的观测, xi=(xi, 1, xi, 2, …, xi, 40)T, vi服从高斯分布N(vi: 0, I40), I40是40维的单位矩阵, H是线性的观测算子。每4个时间步长有观测。
3.3 实验设计在背景协方差放大和分析协方差放大两种情形中, 设置驱动参数F=6、8、9(可以看成模拟的模型误差), 性能水平系数α分别为0. 4和0. 3。考察转移矩阵中的特征值放大实验时, 性能水平系数变化范围α∈[0, 0. 1, 0. 2, …, 0. 9]。为了减少统计的波动, 每个α值重复20次, 每次随机抽取初始背景集合。集合数设置为20。实验主要检查EnTLHF方法对任意初始背景条件的适用性; 检验EnTLHF方法对模型误差变化的鲁棒性; 分析算法参数变化时, EnTLHF方法相比于ETKF方法的性能优劣。实验中均采用无量纲量, 评价的标准是均方根误差(性能水平系数α值的函数)。如下式所示:
| $ RMSE = \frac{{\left\| {{X^t} - {{\bar X}^a}} \right\|}}{{\sqrt m }}, $ | (27) |
式中: xa是分析状态的均值, Xt是真实的状态, ‖·‖表示欧几里得范数, m是系统的维数。
4 数值实验结果及分析敏感性实验是为了比较EnTLHF与ETKF在不同的初始背景条件、强迫参数F及性能水平系数条件下的鲁棒稳健性。
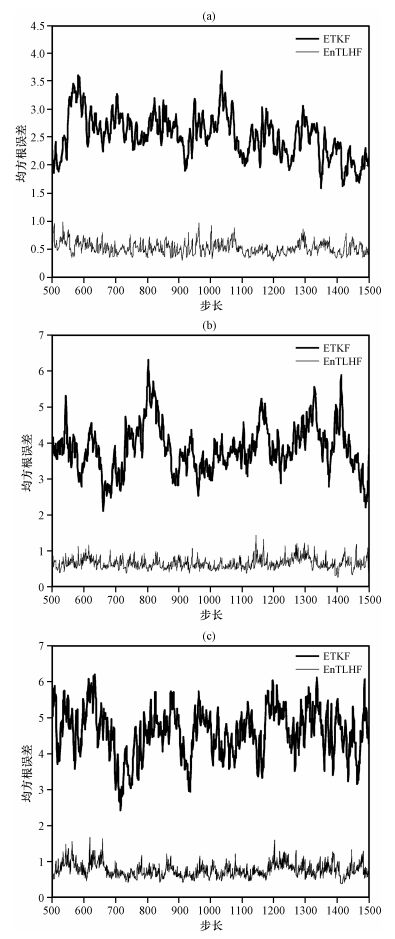
4.1 背景协方差放大实验当α=0. 4, 强迫参数F分别为6, 8, 9时, 图 1给出了ETKF与EnTLHF的均方根误差(RMSE)均值(20次实验取平均)变化图。由图 1可知, ETKF方法中估计误差没有明显的减少。然而, 采用基于鲁棒集合滤波理论的EnTLHF资料同化方法后, 随着同化演进, 估计误差及误差波动明显小于ETKF方法, 说明采用EnTLHF方案得到的分析值精度高。与图 1b和1c相比较, 图 1a中EnTLHF方法的估计误差均小于1;随着强迫参数F的增加, 即模拟增加模型误差, ETKF方法和EnTLHF方法的估计误差都增大, 但EnTLHF方案的性能较为优良, 验证了鲁棒集合资料同化方法的有效性, 同时说明EnTLHF方法对不同程度的模型误差具有较好的鲁棒稳健性。
|
图 1 驱动参数F=6(a)、8(b)和9(c)时, ETKF与背景协方差放大条件下EnTLHF的RMSE均值 Figure 1 Time mean RMSE of ETKF and EnTLHF in the inflation condition of background covariance when the values of the forcing parameters of F are 6 (a), 8 (b) and 9 (c) |
表 1给出了随着F变化, EnTLHF方法与ETKF方法的RMSE均值(先后对1500次, 20次试验取均值)及减小百分比(定义为: EnTLHF方法的RMSE与ETKF方法的RMSE的比值)。
| 表 1 背景协方差放大条件下RMSE的均值及减小的百分比 Table 1 Mean value of RMSE and decrease percentage in the inflation condition of background covariance |
从表 1可以看出, 不论哪种情形, ETKF方法的性能较差, 相比之下, EnTLHF算法即使是在模型误差相对较大时, 也能保证RMSE的均值小于1, 并在一定程度上, 减小误差的百分比超过了15%。
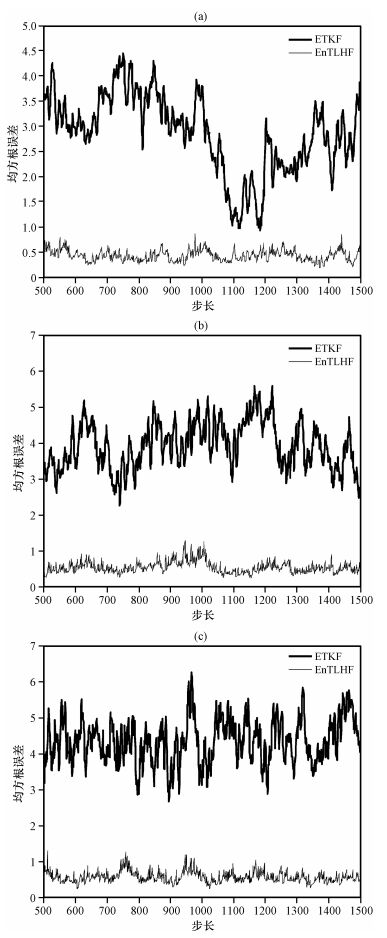
4.2 分析协方差放大实验图 2显示分析协方差放大实验中, 当α=0. 3, 强迫参数F=6, 8, 9, ETKF方法和EnTLHF方法的RMSE变化图。从图 2中可以看出, ETKF方法在每次分析过程中并没有明显的减少估计误差。但是, 采用基于鲁棒集合滤波理论的EnTLHF资料同化方案后, 分析过程中的误差要低于ETKF方法。说明采用EnTLHF方案得到的分析量精度高及鲁棒性能优。随着同化时间的延长, 这种优势依然存在。与F=8和F=9相比较, F=6的RMSE均值小于1;无论F值的大小, EnTLHF方法的估计误差波动程度很小, 而ETKF方法的误差波动在整个同化的过程中较大。进一步说明EnTLHF方法在同化的过程中不仅具有很强的鲁棒稳健性, 而且提高了滤波的精度。
|
图 2 驱动参数F=6(a)、8(b)和9(c)时, ETKF与分析协方差放大条件下EnTLHF的RMSE均值 Figure 2 Time mean RMSE of ETKF and EnTLHF in the inflation condition of analysis covariance when the values of the forcing parameter of F are 6 (a), 8 (b) and 9 (c) |
表 2分别列出了随着F的变化, EnTLHF方法与ETKF方法RMSE的均值(先后对1500次, 20次试验取均值)及误差减小的百分比(EnTLHF方法的RMSE相对ETKF方法的RMSE减小的百分比)。
从表 2中可以看出, 驱动参数F变化时, ETKF算法的性能较差, 相比之下, EnTLHF算法即使是在驱动参数相对较大时, 也能保证RMSE的均值小于1, 说明EnTLHF的性能优于ETKF。
| 表 2 分析协方差放大条件下RMSE的均值以及误差减小的百分比 Table 2 Mean value of RMSE and decrease percentage in the inflation condition of analysis covariance |
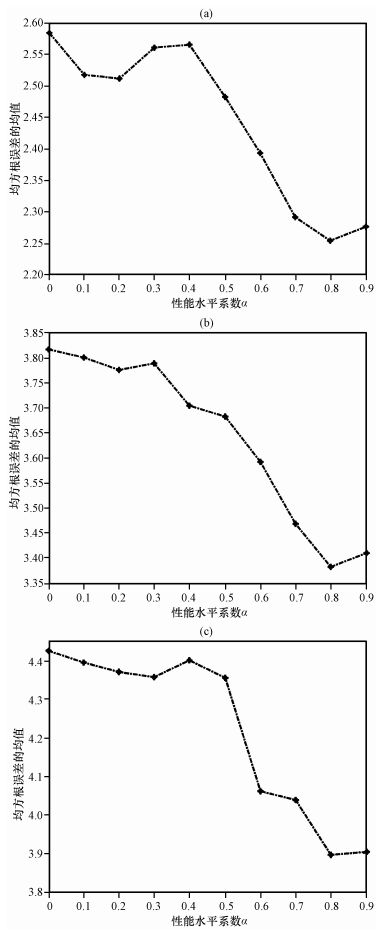
图 3表示转移矩阵放大实验中, 当F分别为6, 8, 9, 且α∈[0, 0. 1, 0. 2, …, 0. 9]时, EnTLHF方法的RMSE随性能水平系数α的变化图。结果显示, 当F=6时, 采用基于鲁棒集合滤波理论的EnTLHF资料同化方法, 放大转移矩阵中的特征值后, α∈[0. 1, 0. 2, …, 0. 9]时的估计误差都小于α=0时的值。说明EnTLHF方法比ETKF方法针对模型误差具有更优的滤波性及更强的鲁棒性。F=8, 9时有类似的结果。随着驱动参数F的增大, 对于相同的性能水平系数α, EnTLHF和ETKF的估计误差都增大, 但是EnTLHF方案的估计误差都小于ETKF方案。进一步验证了基于鲁棒集合资料同化方法放大转移矩阵的有效性, 同时说明该方法具有较好的鲁棒稳健性。
|
图 3 在驱动参数F=6(a)、8(b)和9(c)及不同的α值下, 转移矩阵特征值放大条件下EnTLHF方法的RMSE时间均值 Figure 3 Time mean RMSE of EnTLHF in the inflation condition of transform matrix eigenvalues as PLC changes when the values of the forcing parameter of F are 6 (a), 8 (b) and 9 (c) |
结合H∞滤波的鲁棒性, 从不同的角度分析了几种资料同化协方差放大技术的理论机理。与已有的集合协方差放大技术相比较, EnTLHF提供了统一各类放大技术的理论框架, 并且建立了协方差放大与鲁棒性之间的联系, 推导了ETKF方法和EnTLHF方法的数学表达式, 测试了其鲁棒性。
利用非线性系统Lorenz-96模型, 将传统的ETKF方法和EnTLHF方法进行了比较研究。首先通过背景放大实验和分析放大实验, 考察在固定性能水平系数α, 且改变强迫项F的条件下, 系统模型对两种方法的鲁棒稳健性影响。虽然两种方法的均方根误差随着模型误差的增加而增加, 但结果表明EnTLHF方法的鲁棒性能总是优于ETKF方法, 并且在整个同化的过程中误差的波动程度小, 即EnTLHF方法对模型误差更具鲁棒性。其次, 利用转移矩阵放大新方法, 在改变性能水平系数α时, EnTLHF方法的RMSE总是低于α=0时的ETKF方法的值, 说明基于EnTLHF方法的转移矩阵放大技术提高了鲁棒性并且改进了滤波的性能。
本文引进了估计误差增长率有界的鲁棒滤波理论, 其最大特点是不需要对模型及观测的统计特性做相应的假设。由于其自身的鲁棒性, 参数的变化并不会影响滤波的性能。该方法可广泛应用于其他非线性系统的资料同化中。
| Altaf M U, Butler T, Luo X, et al. 2013. Improving short-range ensemble Kalman storm surge forecasting using robust adaptive inflation[J]. Mon Wea Rev, 141(8): 2705–2720. DOI:10.1175/MWR-D-12-00310.1 | |
| Anderson J D. 1999. Aircraft Performance and Design[M]. Boston: WCB/McGraw Hill, 406-453. | |
| Bishop C H, Etherton B J, Majumdar S J. 2001. Adaptive sampling with the ensemble transform Kalman filter. Part Ⅰ:Theoretical aspects[J]. Mon Wea Rev, 129(3): 420–436. DOI:10.1175/1520-0493(2001)129<0420:ASWTET>2.0.CO;2 | |
| Bocquet M, Sakov P. 2012. Combining inflation-free and iterative ensemble Kalman filters for strongly nonlinear systems[J]. Nonlinear Processes in Geophysics, 19(3): 383–399. DOI:10.5194/npg-19-383-2012 | |
| Evensen G. 2003. The ensemble Kalman filter:Theoretical formulation and practical implementation[J]. Ocean Dyn, 53(4): 343–367. DOI:10.1007/s10236-003-0036-9 | |
| Jaison T A, Youmin T. 2009. Sigma-Point Kalman Filter Data Assimilation Methods for Strongly Nonlinear Systems"[J]. Atmos Sci, 66: 261–285. DOI:10.1175/2008JAS2681.1 | |
| Hamill T M. 2001. An overview of ensemble forecasting and data assimilation[C] //conference on weather analysis and forecasting. 18:353-357. | |
| Hoteit I, Pham D T, Blum J. 2002. A simplified reduced order Kalman filtering and application to altimetric data assimilation in Tropical Pacific[J]. Journal of Marine systems, 36(1): 101–127. | |
| Julier S J. 2003. The spherical simplex unscented transformation[C] //American Control Conference, 2003. Proceedings of the 2003. IEEE, 3:2430-2434. | |
| Lorenz E N, Emanuel K A. 1998. Optimal sites for supplementary weather observations:Simulation with a small model[J]. J Atmos Sci, 55(3): 399–414. DOI:10.1175/1520-0469(1998)055<0399:OSFSWO>2.0.CO;2 | |
| Luo X D, Hoteit I. 2013. Covariance inflation in the ensemble Kalman filter:A residual nudging perspective and some implications[J]. Mon Wea Rev, 141(10): 3360–3368. DOI:10.1175/MWR-D-13-00067.1 | |
| Luo X D, Hoteit I. 2014. Ensemble Kalman filtering with residual nudging:An extension to state estimation problems with nonlinear observation operators[J]. Mon Wea Rev, 142(10): 3696–3712. DOI:10.1175/MWR-D-13-00328.1 | |
| Luo X D, Hoteit I. 2011. Robust ensemble filtering and its relation to covariance inflation in the ensemble Kalman filter[J]. Mon Wea Rev, 139(12): 3938–3953. DOI:10.1175/MWR-D-10-05068.1 | |
| Miyoshi T, Bishop C, Kalnay E, et al. 2011. FY2011 annual report of data assimilation and predictability studies for improving tropical cyclone intensity forecasts[R]. Maryland Univ College Park Dept of Atmospheric and Oceanic Science. | |
| Petersen G N, Majumdar S J, Thorpe A J. 2007. The properties of sensitive area predictions based on the ensemble transform Kalman filter (ETKF)[J]. Quart J Roy Meteor Soc, 133(624): 697–710. DOI:10.1002/(ISSN)1477-870X | |
| Qiu C, Shao A, Xu Q, et al. 2007. Fitting model fields to observations by using singular value decomposition:An ensemble-based 4DVar approach[J]. Geophys Res Atmos, 112(D11): 236–242. | |
| Sakov P, Bertino L. 2011. Relation between two common localisation methods for the EnKF[J]. Computational Geosciences, 15(2): 225–237. DOI:10.1007/s10596-010-9202-6 | |
| Simon D. 2006. Optimal state estimation:Kalman, H infinity, and nonlinear approaches[M]. John Wiley & Sons. | |
| Triantafyllou G, Hoteit I, Luo X, et al. 2013. Assessing a robust ensemble-based Kalman filter for efficient ecosystem data assimilation of the Cretan Sea[J]. Journal of Marine Systems, 125: 90–100. DOI:10.1016/j.jmarsys.2012.12.006 | |
| Wang D, Cai X. 2008. Robust data assimilation in hydrological modeling-A comparison of Kalman and H-infinity filters[J]. Adv WaterResour, 31(3): 455–472. | |
| Wang X, Bishop C H, Julier S J. 2004. Which is better, an ensemble of positive-negative pairs or a centered spherical simplex ensemble?[J]. Mon Wea Rev, 132(7): 1590. DOI:10.1175/1520-0493(2004)132<1590:WIBAEO>2.0.CO;2 | |
| Whitaker J S, Hamill T M. 2002. Ensemble data assimilation without perturbed observations[J]. Mon Wea Rev, 130(7): 1913–1924. DOI:10.1175/1520-0493(2002)130<1913:EDAWPO>2.0.CO;2 | |
| 胡春梅, 陈道劲, 于润玲. 2010. BP神经网络和支持向量机在紫外线预报中的应用[J]. 高原气象, 29(2): 539–544. Hu Chunmei, Chen Daojin, Yu Runling. 2010. Application of BP artificial neural network and support vector machines to ultraviolet radiation prediction[J]. Plateau Meteor, 29(2): 539–544. | |
| 李虎超, 邵爱梅, 何邓新, 等. 2015. BP神经网络在估算模式非系统性预报误差中的应用[J]. 高原气象, 34(6): 1751–1757. DOI:10.7522/j.issn.1000-0534.2014.00120 Li Huchao, Shao Aimei, He Dengxin, et al. 2015. Application of back-propagation neural network in predicting non-systematic error in numerical prediction model[J]. Plateau Meteor, 34(6): 1751–1757. DOI:10.7522/j.issn.1000-0534.2014.00120 | |
| 刘亚亚, 毛节泰, 刘钧, 等. 2010. 地基微波辐射计遥感大气廓线的BP神经网络反演方法研究[J]. 高原气象, 29(6): 1514–1523. Liu Yaya, Mao Jietai, Liu Jun, et al. 2010. Research of BP neural network for microwave radiometer remote sensing retrieval of temperature, relative humidity, cloud liquid water profiles[J]. Plateau Meteor, 29(6): 1514–1523. | |
| 邱晓滨, 邱崇践. 2009. 混合误差协方差用于集合平方根滤波同化的试验[J]. 高原气象, 28(6): 1399–1407. Qiu Xiaobin, Qiu Chongjian. 2009. The suitability test of Ensemble square root filter with hybrid background error covariance[J]. Plateau Meteor, 28(6): 1399–1407. | |
| 邵爱梅, 邱晓滨, 邱崇践. 2011. 使用混合样本的集合四维变分同化试验研究[J]. 高原气象, 30(3): 583–593. Shao Aimei, Qiu Xiaobin, Qiu Chongjian. 2011. Ensemble-based four-dimensional variational assimilation using hybrid samples[J]. Plateau Meteor, 30(3): 583–593. |
 2017, Vol. 36
2017, Vol. 36