2. 中国人民解放军国防科学技术大学海洋科学与工程研究院, 长沙 410073
数值模式动力框架核心是空间离散化和时间积分方案, 它决定模式描述大气运动数学特性(包括模式精度)、物理保守性和计算稳定性。谱模式以欧洲中期天气预报中心(ECMWF)为代表。周毅等(2002)认为, 谱(球谐函数)具备对原函数“收敛性”(较准确计算空间微商)和“最优性”(最小平方误差逼近), 且为实现高次代数精确度的高斯积分公式与计算谱分量(谱系数), 必然选择采用纬向等距、经向不等距(勒让德多项式零点)的高斯网格, 即通过勒让德变换确定高斯网格坐标与高斯积分公式的求和系数, 并且通过“离散傅里叶变换(DDT)”或“快速傅里叶变换(FFT)”求得变量场谱分量, 或由谱分量合成高斯网格上的变量值。但作高斯网格二维谱展开还存在一些数学与计算缺陷:除高斯积分公式存在“多项求和代替积分”误差之外, 谱展开不可避免地存在波数截断误差, 在洋面上存在虚假的谱地形波(Gibbs现象), 矢量场(水平风及加速度)在极点为数学奇点, 不适合做谱展开, 故高斯网格不含极点(不对极点做预报), 则谱展开关于极点不对称(仅关于赤道对称), 且谱不适合做全球/区域统一数值模式、不适合做中尺度模式, 模式垂直方向不适合于谱, 另外, 随着模式分辨率的提高, 谱计算量迅速增加, 其提高模式计算精度的效率却迅速降低。
由于谱模式的局限性, 自20世纪90年代末以来, 世界上一些国家(如英国、美国、加拿大、法国、日本和中国)重新转向研究水平分辨率从1~100 km的全球/区域统一(格点)数值模式(Côté et al, 1998a, 1998b; Bubnová et al, 1995; 薛纪善和陈德辉, 2008)。但是, 格点模式同样遇到一些数学困难:如在经纬网格上, 存在极区网格点过密与两极奇异点, 欧拉差分方案计算精度不高, 其时间积分受约束于CFL计算稳定性条件等。
中国研究开发的GRAPES全球/区域统一数值模式(薛纪善和陈德辉, 2008), 采用球面经纬网格与SI-SL积分方案, 且必须求解庞大计算量的“三维气压扰动”广义共轭余差Helmholtz方程, 即采用Ritchie and Beaudoin (1994)计算准拉格朗日上游点路径方案, 在极区采用McDonald and Bates (1989)旋转格点计算上游点(Lagrangian particle)路径方案, 但不对极点作预报。一般认为(陈德辉等, 2004), 空间差分截断误差要比时间差分截断误差大得多, 采用准拉格朗日差分方案, 不仅可提高空间差分计算精度, 且使得时间步长只依据准拉格朗日差分方案计算精度, 而不再依据欧拉差分方案计算稳定度, 故准拉格朗日积分方案在静力/非静力模式中得到广泛应用(Cullen, 1990; Cullen et al, 1997)。但薛纪善和陈德辉(2008)认为, 相对于欧拉差分守恒方案, 准拉格朗日差分守恒方案的理论设计非常困难, 表明国内外至今尚未研究出准拉格朗日守恒积分方案全球格点模式。另外, 为克服极区网格点过密问题, 有人正在研究做“阴阳网格”数值模式(李江浩和彭新东, 2013; Li et al, 2006), 但阴阳网格不属于经纬网格, 而若做“经纬网格-阴阳网格”切换插值, 又将带来新的计算误差。
本文借鉴谱模式动力框架核心思想, 高斯网格二维谱变换半隐式-半拉格朗日积分方案(semi-implic semi-Lagrangian integration scheme, SI-SL), 探究准均匀经纬网格三次样条函数变换显式-准拉格朗日积分方案(explicit quasi-Lagrangian integration scheme)。应该指出, ECMWF谱模式采用了高斯网格(网格点从赤道向两极递减), 但因极点为(水平矢量场)数学奇点, 实际采用了一种“偏极点”准均匀经纬网格。
三次样条函数“变换”属于Hermite二重密切(二阶可导)“拟合+插值”(奚梅成, 1995)。三次样条函数分为“线、面、体”, 即三次样条(cubic spline)、双三次曲面(bicubic surface, Fergusion, 1964) 和三次曲体(tricubic cube), 而以三次样条(样条格式)为数学基础, 有数学定律(可推广到三次曲面和曲体): (1) 三次样条及其1阶、2阶导数收敛于原函数及其1阶、2阶导数(收敛性); (2) 三次样条二阶导数对原函数二阶导数为最佳逼近(最优性); (3) 三次样条既是二阶空间精度差分格式(精确性), 又是二阶可导积分格式(可积分性); (4) 三次样条存在多种数学边界(边界适应性), 且存在周期三次样条函数(周期三次样条无边界); (5) 自然三次样条函数具有最小总曲率(趋稳性); (6) 三次样条存在光顺泛函数(可光顺性), 以消除“多余拐点”(二拐点)和不连续“尖点”或“环绕”(二重合点); (7) 三次样条可保持点对称性(关于极点、经向、纬向对称), 而双三次曲面可保持球(面)对称性(关于极点、经向、纬向、经圈和赤道对称); (8) 三次样条可拼接其它连续函数(拼接性), 如三次样条可拼接二次、线性函数(无Gibbs现象)。以下将三次样条函数全部数学性质统称为“样条格式”, 且将三次样条函数变换, 变换=拟合+插值, 简称为“样条变换”。
所以, 采用三次样条函数, 完全具备做全球/区域统一样条格式(格点)数值模式(简称“样条模式”)的数学基础, 这既是格点模式的可能发展方向, 又能够克服谱模式相对于格点模式既有的缺点。如格点模式一般未考虑计算(三次曲面和曲体具有的)挠率, 三次样条函数具备完全“二阶空间”计算精度, 其高于“线性”中央差和“双线性”Lagrange三次函数插值(样条模式计算精度将高于一般格点模式)。将来还可以比较高斯网格谱展开与准均匀经纬网格双三次曲面拟合求上游点, 谁的计算精度高, 谁的数学收敛性更适合做数值模式, 并且通过做理想试验, 认识它们各自的优缺点, 或者探究高斯网格勒让德函数与三次样条函数变换相结合的全球/区域统一数值模式。
吕美仲等(1983)采用样条格式对正压原始方程做欧拉差分半隐式积分方案, 经试验于一维平流方程证明, 样条格式计算精度高于中央差2阶、4阶格式精度, 同时给出一种用三次样条函数求解Helmholtz方程迭代法, 并且证明迭代的收敛性, 给出计算个例表明, 样条格式较中央差格式更为稳定, 可较少使用平滑, 其预报天气系统波相速和波振幅较为准确。Layton(2002)在球面坐标上, 采用样条格式对浅水波方程做欧拉差分半隐式“蛙跳”三时间层积分方案, 经积分试验表明, 它是一种高阶(三次)精确且计算稳定的方法, 相比之下, 谱方法将遇到高阶勒让德变换复杂性。辜旭赞(2010, 2011)用泰勒级数展开, 完成四阶时空余差准拉格朗日法和欧拉法的对接推导, 证明用三次样条函数插值求准拉格朗日法上游点路径、或设计用样条格式斜率、曲率和挠率求欧拉法位移, 两种方法的数学基础一致, 同为二阶时空精度的数值解, 也可以求四阶时空精度的数值解, 但三次样条拟合计算量将呈指数增长。
2 样条格式准拉格朗日预报方程 2.1 大气运动方程球面坐标原始大气运动方程为(设为无地形、无水汽源汇, 并设时间t, 气压p、气温T、比湿q、V=(u, v, w)为三维风场, 气块至地心距离r, 但取r=r0, r0为地球平均半径, λ(λ∈[0, 2π])、φ(φ∈[-π/2, π/2])为经、纬度, 并δx=r0cosφδλ, δy=r0δφ, δr=δz, 以及f=2Ωsinφ、
| $ \frac{{{\rm{d}}u}}{{{\rm{d}}t}} = - RT\frac{{\partial \ln p}}{{\partial x}} + fv - \tilde fw + \frac{{uv \cdot \tan \varphi - uw}}{{{r_0}}} + {F_u}\hat = {a_u}, $ | (1) |
| $ \frac{{{\rm{d}}v}}{{{\rm{d}}t}} = - RT\frac{{\partial \ln p}}{{\partial y}} - fu - \frac{{{u^2}\tan \varphi + vw}}{{{r_0}}} + {F_v}\hat = {a_v}, $ | (2) |
| $ \frac{{{\rm{d}}w}}{{{\rm{d}}t}} = - RT\frac{{\partial \ln p}}{{\partial z}} - g + \tilde fu + \frac{{{u^2} + {v^2}}}{{{r_0}}} + {F_w}\hat = {a_w}, $ | (3) |
| $ \frac{{\partial \ln p}}{{\partial t}} = \frac{{ - 1}}{{1 - \kappa }}\nabla \cdot V\hat = {a_p}, $ | (4) |
| $ \frac{{\partial \ln T}}{{\partial t}} = \frac{{ - \kappa }}{{1 - \kappa }}\nabla \cdot V\hat = {a_T}, $ | (5) |
| $ \frac{{{\rm{d}}q}}{{{\rm{d}}t}} = 0, $ | (6) |
因u与u方程在极点无定义, 而v与v方程在极点有定义。先定义北、南极点(分别用下标N和S表示)与0°E u平行(λ=0) 分量为uN和uS, 而与0°E v平行分量(λ=π9/2) 为vN和vS, 则对于(uN, vN)和(uS, vS), (任何水平矢量)都可以作如下三角函数矢量分解:
| $ \left\{ \begin{array}{l} {u_{N\left( \lambda \right)}} = {u_N}\cos \lambda + {v_N}\sin \lambda \\ {u_{S\left( \lambda \right)}} = {u_S}\cos \lambda - {v_S}\sin \lambda \\ {v_{N\left( \lambda \right)}} = {v_N}\cos \lambda - {u_N}\sin \lambda \\ {v_{S\left( \lambda \right)}} = {v_S}\cos \lambda - {u_S}\sin \lambda \end{array} \right., $ | (7) |
容易证明, 上式有
| $ \frac{{{\rm{d}}{u_N}}}{{{\rm{d}}t}} = - RT{\left( {\frac{{\partial \ln p}}{{\partial y}}} \right)_{N\left( {3{\rm{\pi /2}}} \right)}} + f{v_N} - \frac{{{u_N}w}}{{{r_0}}} + {F_v}, $ | (8) |
| $ \frac{{{\rm{d}}{u_S}}}{{{\rm{d}}t}} = - RT{\left( {\frac{{\partial \ln p}}{{\partial y}}} \right)_{S\left( {{\rm{\pi /2}}} \right)}} + f{v_S} - \frac{{{u_S}w}}{{{r_0}}} + {F_v}, $ | (9) |
| $ \frac{{{\rm{d}}{v_N}}}{{{\rm{d}}t}} = - RT{\left( {\frac{{\partial \ln p}}{{\partial y}}} \right)_{N\left( 0 \right)}} + f{u_N} - \frac{{{v_N}w}}{{{r_0}}} + {F_v}, $ | (10) |
| $ \frac{{{\rm{d}}{v_S}}}{{{\rm{d}}t}} = - RT{\left( {\frac{{\partial \ln p}}{{\partial y}}} \right)_{S\left( {\rm{0}} \right)}} - f{u_S} - \frac{{{v_S}w}}{{{r_0}}} + {F_v}. $ | (11) |
设P表示p、T、q、u、v、w等, 已知P的一阶时间全导数(变率)为
设欧拉点(x, y, z)预报变量为P(t+Δt, x, y, z), Δt为时间步长, 且设P的二阶时间变率为
| $ \begin{array}{l} P\left( {t + \Delta t,x,y,z} \right) = P\left( {t,x - \Delta x,y - \Delta y,z - \Delta z} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + a\left( {t,x - \Delta x,y - \Delta y,z - \Delta z} \right)\Delta t\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + a'\left( {t,x - \Delta x,y - \Delta y,z - \Delta z} \right)\frac{{\Delta {t^2}}}{2}, \end{array} $ | (12) |
上式三维上游点P(t, x-Δx, y-Δy, z-Δz)仅取泰勒级数“二阶空间余差”近似:
| $ \begin{array}{l} P\left( {t,x - \Delta x,y - \Delta y,z - \Delta z} \right) \approx P\left( {t,x,y,z} \right) - \Delta x\frac{{\partial P}}{{\partial x}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\; - \Delta y\frac{{\partial P}}{{\partial y}} - \Delta z\frac{{\partial P}}{{\partial z}} + \frac{{{\Delta ^2}x}}{2}\frac{{{\partial ^2}P}}{{\partial {x^2}}} + \frac{{{\Delta ^2}y}}{2}\frac{{{\partial ^2}P}}{{\partial {y^2}}} + \frac{{{\Delta ^2}z}}{2}\frac{{{\partial ^2}P}}{{\partial {z^2}}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\; + \Delta x\Delta y\frac{{{\partial ^2}P}}{{\partial x\partial y}} + \Delta x\Delta z\frac{{{\partial ^2}P}}{{\partial x\partial z}} + \Delta y\Delta z\frac{{{\partial ^2}P}}{{\partial y\partial z}}, \end{array} $ | (13) |
同理(同式(13)), 可给出二阶空间余差上游点1、2阶时间变率a和a′。
并按牛顿运动定律, 求取二阶时间余差上游点三维运动路径(位移)(Δx, Δy, Δz)及其坐标(x-Δx, y-Δy, z-Δz):
| $ \left\{ \begin{array}{l} \Delta x = u\left( {t,x - \Delta x,y - \Delta y,z - \Delta z} \right)\Delta t\\ \;\;\;\;\;\;\;\; + {a_u}\left( {t,x - \Delta x,y - \Delta y,z - \Delta z} \right)\frac{{{\Delta ^2}t}}{2}\\ \Delta y = v\left( {t,x - \Delta x,y - \Delta y,z - \Delta z} \right)\Delta t\\ \;\;\;\;\;\;\;\; + {a_v}\left( {t,x - \Delta x,y - \Delta y,z - \Delta z} \right)\frac{{{\Delta ^2}t}}{2}\\ \Delta z = w\left( {t,x - \Delta x,y - \Delta y,z - \Delta z} \right)\Delta t\\ \;\;\;\;\;\;\;\; + {a_w}\left( {t,x - \Delta x,y - \Delta y,z - \Delta z} \right)\frac{{{\Delta ^2}t}}{2} \end{array} \right., $ | (14) |
实际应采用迭代法计算上游点位移(坐标)与物理量, 迭代初值不妨就取u(t, x, y, z)、v(t, x, y, z)、w(t, x, y, z)、au(t, x, y, z)、av(t, x, y, z)、aw(t, x, y, z)。
另外, Δx在极点无定义, 但在北、南极点有水平矢量ΔxN=ΔyN(3π/2)和ΔxS=ΔyS(π/2)。
2.3 样条格式二阶时空离散预报方程因三次样条函数具有数学定律“二阶可导‘收敛性’和‘最优性’”及适当三次样条边界, 故采用三次样条函数拟合求解完全“二阶空间余差”三维上游点(参见式(13))。即做变量(P)场三次样条函数拟合, 实现P场“线、面、体”二阶可导, 求得斜率Px、Py、Pz, 曲率Pxx、Pyy、Pzz和挠率Pxy、Pxz、Pyz。所谓“样条格式”即是认为式(8) 中:
| $ \begin{gathered} P\left( {t,x - \Delta x,y - \Delta y,z - \Delta z} \right) \approx P\left( {t,x,y,z} \right) - \Delta x{P^x} \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\; - \Delta y{P^y} - \Delta z{P^z} + \frac{{\Delta {x^2}}}{2}{P^{xx}} + \frac{{\Delta {y^2}}}{2}{P^{yy}} + \frac{{\Delta {z^2}}}{2}{P^{zz}} \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\; + \Delta x\Delta y{P^{xy}} + \Delta x\Delta z{P^{xz}} + \Delta y\Delta z{P^{yz}} \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\; = \dddot P\left( {t,x - \Delta x,y - \Delta y,z - \Delta z} \right), \hfill \\ \end{gathered} $ | (15) |
上式适合求“非静力”上游点。若(15) 式略去水平-垂直挠率Pxz和Pyz高阶小项, 但仍保留水平“经-纬”挠率Pxy项, 其变为:
| $ \begin{gathered} \dddot P\left( {t,x - \Delta x,y - \Delta y,z - \Delta z} \right) \approx P\left( {t,x,y,z} \right) - \Delta x{P^x} \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\; - \Delta y{P^y} - \Delta z{P^z} + \frac{{\Delta {x^2}}}{2}{P^{xx}} + \frac{{\Delta {y^2}}}{2}{P^{yy}} + \frac{{\Delta {z^2}}}{2}{P^{zz}} + \Delta x\Delta y{P^{xy}} \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\; = \ddot P\left( {t,x - \Delta x,y - \Delta y,z} \right) - \Delta z{P^z} + \frac{{{\Delta ^2}z}}{2}{P^{zz}}, \hfill \\ \end{gathered} $ | (16) |
式中:
从而有样条格式准拉格朗日二阶时空余差预报方程通式(参见式(12)):
| $ \begin{gathered} P\left( {t + \Delta t,x,y,z} \right) = \dddot P\left( {t,x - \Delta x,y - \Delta y,z - \Delta z} \right) \hfill \\ \;\;\;\;\;\;\;\;\; + \dddot a\left( {t,x - \Delta x,y - \Delta y,z - \Delta z} \right)\Delta t \hfill \\ \;\;\;\;\;\;\;\;\; + \dddot a'\left( {t,x - \Delta x,y - \Delta y,z - \Delta z} \right)\frac{{\Delta {t^2}}}{2}, \hfill \\ \end{gathered} $ | (17) |
上式简记为:
| $ {P^{t + \Delta t}} = \dddot P + \dddot a\Delta t + \dddot a'\frac{{\Delta {t^2}}}{2}, $ | (18) |
对式(18), 因P的二阶变率a′一般为未知, 若假设Δt时段内
| $ {P^{t + \Delta t}} = \dddot P + \dddot a\Delta t, $ | (19) |
而若假设Δt时段内
| $ {P^{t + \Delta t}} = \dddot P + \dddot a\Delta t + c\frac{{\Delta {t^2}}}{2}, $ | (20) |
对上式, 可代入P=a, 且考虑到P的二阶变率(a的一阶变率)为c, 有:
| $ {a^{t + \Delta t}} = \dddot a + \dddot a'\Delta t = \dddot ac\Delta t, $ | (21) |
则求得
| $ {P^{t + \Delta t}} = \dddot P + \left( {{a^{t + \Delta t}} + \dddot a} \right)\frac{{\Delta t}}{2}, $ | (22) |
上式的计算精度高于“匀加速”显式预报方程(式(19))。
上述预报方程表明:若准拉格朗日气块不与外界发生任何物理交换(变率为零), 则欧拉点预报值就等于上游点值。但是, 上游点一般都经过非线性路径, 而式(16)~(17) 是气块在Δt时段内, 沿“样条格式”路径, 带着全部物理属性, 并且受到各自变率作用, 到达欧拉预报点。
显然, 若欧拉法预报方程也采用上述样条格式(参见式(16))做二阶时空离散格点设计, 包括变量和变率场斜率、曲率和挠率设计, 将是非常困难的。
3 样条格式与中央差比较 3.1 非线性样条格式样条格式是以“3点”为主, 但关于全局(全部格点)的“二阶可导”非线性格式, 须已知4个(以上)格点值和2个端点边界条件才可以做三次样条拟合(奚梅成, 1995), 三次样条拟合采用所谓“追赶法”, 它是从一个端点到另一个端点“逐点”求解。
对于离散等距ΔX变量场Pj, j=0, ±1, ±2, …, ±J, 三次样条拟合斜率mj和曲率Mj与一阶中央差mj和二阶中央差Mj有如下数学关系(样条格式与中央差数学关系, 奚梅成, 1995):
| $ \begin{array}{l} {{\bar m}_j} = {m_j} + \frac{{{m_{j + 1}} - 2{m_j} + {m_{j - 1}}}}{6}\\ \;\;\;\;\; = \frac{{{P_{j + 1}} - {P_{j - 1}}}}{{2\Delta X}}, \end{array} $ | (23) |
| $ \begin{array}{l} {{\bar M}_j} = {M_j} + \frac{{{M_{j + 1}} - 2{M_j} + {M_{j - 1}}}}{6}\\ \;\;\;\;\; = \frac{{{P_{j + 1}} - 2{P_j} + {P_{j - 1}}}}{{\Delta {X^2}}}, \end{array} $ | (24) |
式(23)、(24) 表明, 中央差斜率和曲率, 分别就是三次样条斜率和曲率作系数为1/3的“三点平滑”, 故中央差近似总是减小大气波动振幅和减慢其相速(周毅等, 2002), 这应与中央差对三次样条的拟合斜率和曲率做三点平滑有关。
3.2 样条格式线性截断误差样条格式为非线性格式, 但样条格式曲率Mj的“线性部分”就是二阶中央差Mj(奚梅成, 1995), 而样条格式斜率mj由曲率Mj决定(二者不独立)。故分析对比二阶中央差Mj与一阶中央差mj的空间截断误差, 对于更加清楚的认识样条格式是有帮助的(张玉玲等, 1986)。
设变量场P为简谐波: P=exp(ikx), 已设波振幅为1,
| $ \frac{{\partial P}}{{\partial x}} = ik\exp \left( {ikx} \right), $ | (25) |
| $ \frac{{{\partial ^2}P}}{{\partial {x^2}}} = - {k^2}\exp \left( {ikx} \right), $ | (26) |
令x=jΔX, 可以用一阶中央差分mj近似表示一阶偏微商:
| $ \begin{array}{l} {{\bar m}_j} = \frac{{{P_{j + 1}} - {P_{j - 1}}}}{{2\Delta X}}\\ \;\;\;\;\; = \frac{{\exp \left[ {ik\left( {j + 1} \right)\Delta X} \right] - \exp \left[ {ik\left( {j - 1} \right)\Delta X} \right]}}{{2\Delta X}}\\ \;\;\;\;\; = \frac{{i\sin k\Delta X}}{{\Delta X}}\exp \left( {ikj\Delta X} \right), \end{array} $ | (27) |
对比式(27) 与(25), 可知mj格式的波数(设为km)为:
| $ {k_m} = \frac{{\sin k\Delta X}}{{\Delta X}}, $ | (28) |
同理, 可以用二阶中央差分Mj近似表示二阶偏微商:
| $ \begin{array}{l} {{\bar M}_j} = \frac{{{P_{j + 1}} - 2{P_j} + {P_{j - 1}}}}{{\Delta {X^2}}}\\ \;\;\;\;\; = \frac{{\exp \left[ {ik\left( {j + 1} \right)\Delta X} \right] - 2\exp \left( {ikj} \right)\Delta X + \exp \left[ {ik\left( {j - 1} \right)\Delta X} \right]}}{{\Delta {X^2}}}\\ \;\;\;\;\; = - \frac{{2\left( {1 - \cos k\Delta X} \right)}}{{\Delta {X^2}}}\exp \left( {ikj\Delta X} \right), \end{array} $ | (29) |
对比式(29) 与(26), 可知Mj格式的波数(设为kM)为:
| $ {k_M} = \frac{{{{\left[ {2\left( {1 - \cos k\Delta X} \right)} \right]}^{\frac{1}{2}}}}}{{\Delta X}}, $ | (30) |
设
| 表 1 一阶导数中央差mj与二阶导数中央差Mj拟合简谐波空间截断误差Rm和RM(比值)、相速cm和cM、群速Cm和CM Table 1 Space truncation errors Rm and RM (ratio), phase velocities cm and cM, and group velocities Cm and CM of the first-order and second-order center differentials mj and Mj |
由表 1知, 可用三角函数倍角公式予以证明:Mj格式比mj格式空间截断误差减少一倍, 即前者比后者空间分辨率和拟合精确度提高一倍, 尤其在短波波长范围提高明显, 例如, 波长L=4ΔX的Mj格式与波长L=8ΔX的mj格式空间分辨率及空间截断误差基本一致。
3.3 样条格式线性相速、群速与误差因欧拉一维平流方程(设一维流场u0为常数, 即假定真解相速和群速均为u0):
| $ \frac{{\partial P}}{{\partial t}} + {u_0}\frac{{\partial P}}{{\partial x}} = 0, $ | (31) |
作
| $ \frac{{{\partial ^2}P}}{{\partial {t^2}}} - u_0^2\frac{{{\partial ^2}P}}{{\partial {x^2}}} = 0, $ | (32) |
设有“简谐波”特解: Pj(x, t)=exp[i(kjΔX-ωt)], ω为圆频率, 将其分别代入式(31)、(32), 同时, 分别用mi格式和Mj格式近似代替式(31) 一阶偏微商和式(32) 二阶偏微商, 整理为:
| $ i\left( { - \omega + {u_0}\frac{{\sin k\Delta X}}{{\Delta X}}} \right)\exp \left[ {i\left( {kj\Delta X - \omega t} \right)} \right] = 0, $ | (33) |
| $ \left[ { - {\omega ^2} + u_0^2\frac{{2\left( {1 - \cos k\Delta X} \right)}}{{\Delta {X^2}}}} \right]\exp \left[ {i\left( {kj\Delta X - \omega t} \right)} \right] = 0, $ | (34) |
可由式(33) 求得mj格式相速cm和群速Cm, 由式(34) 求得Mj格式相速cM和群速CM:
| $ {c_m} = \frac{\omega }{k} = {u_0}\frac{{\sin k\Delta X}}{{k\Delta X}}, $ | (35) |
| $ {C_m} = \frac{{\partial \omega }}{{\partial k}} = {u_0}\cos k\Delta X, $ | (36) |
| $ {c_M} = {u_0}\frac{{{{\left[ {2\left( {1 - \cos k\Delta X} \right)} \right]}^{\frac{1}{2}}}}}{{k\Delta X}}, $ | (37) |
| $ {C_M} = {u_0}\frac{{\sqrt 2 \sin k\Delta X}}{{2{{\left( {1 - \cos k\Delta X} \right)}^{\frac{1}{2}}}}}, $ | (38) |
由式(35)~(38) 与表 1可知, 且可用三角函数倍角/半角公式给予证明: Mj格式比mj格式减少相速和群速误差一倍, 尤其在短波波长范围提高明显, 例如, 波长L=4ΔX的Mj格式与波长L=8ΔX的mj格式相速和群速误差一样。但mj格式和Mj格式相速(及群速)均与波数有关, 均为所谓“频散波”(真解为非频散波), 且二者的相速和群速均慢于真解:mj格式|Cm|<|cm|≤1和Mj格式|CM|<|cM|≤1, 表明两种格式均为“群速慢于相速慢于真实气流”(两种计算波相对于基本气流均为逆向传播, 并且能量逆向频散快于位相逆向传播), 波长越短, 误差越大, 其能量频散为:在扰动上游产生新的波动、或使得原有的波动增强, 出现所谓“上游/下游(向下游传播)效应”, 一方面对预报天气系统移动与新生很重要, 另一方面可能导致出现“寄生(短)波”(一种计算假波)(张玉玲等, 1986), 寄生波在基本气流上游方向(能量向上游方向频散)逐渐形成, 并向下游传播, 寄生波发展可能造成某一变量场的计算(预报)紊乱。
以上分析是以二阶中央差Mj格式代表样条格式“线性部分”, 并且分析对比二阶中央差Mj与一阶中央差mj的空间截断误差、相速和群速及其误差, 证明二阶中央差优于一阶中央差, 从而认为, 非线性样条格式应是三者之间最优的。
4 准均匀经纬网格设计 4.1 球面经纬网格全球样条模式采用球面Z(位势高度)坐标系。下面以球面1°×1°经纬网格(“A网格”)作叙述, 更高水平分辨率可按比例推算。
1°×1° A网格共有(0:360, 0:180)65160个网格点。为采用周期三次样条做拟合, 在纬向取0°E/0°W为重合点, 即设定变量场在起始点‘0’(0°E)值始终等于终止点‘360’(0°W)值; 并且标量场(如p、T、q)及垂直矢量场(如w)在两极点始终赋予360个相同值, 而水平矢量场(如(u, v)、(au, av))始终赋予360个不同“三角函数”分解值(参见式(7))。
4.2 准均匀经纬网格在上述A网格基础上, 首先设计两种基本的准均匀经纬网格(表 2): ① 从赤道向两极分段成倍递减A网格点(“B网格”), B网格保持纬向等距且B网格点与A网格点重合; ② 分段线性递减A网格点数目(“J网格”), J网格保持纬向等距且J网格点(除赤道和极点外)一般不与A网格点重合。
| 表 2 球面1°×1°经纬网格(A网格)和两种准均匀经纬网格(B网格和J网格) Table 2 The global 1°×1° latitude-longitude grid (A-grid), the quasi-uniform titude-longitude grid (B-grid), and the quasi-uniform titude-longitude grid (J-grid) |
由表 2可见, B网格和J网格都减少了高纬带网格点, 使得网格点纬距相对于经距为“准均匀”, 但B网格和J网格不能够直接做经向三次样条拟合, 且B网格存在2倍格距过渡界线(表 2中的60°N/60°S), 在积分过程中容易造成所谓的“非线性混淆误差”:样条格式也可能产生2倍格距虚假短波, 从高纬带(经过这里)传播到中-低纬带; 而J网格无2倍格距过渡界线。故实现准均匀(变)经纬网格样条变换积分方案的核心思想是只做B或J网格点预报, 但做全部A网格点预报插值。
对应于B网格和J网格, 存在如下的积分流程(以“静力平流”为例):
(1) A-B流程(A-B网格切换): ① 在A网格上, 做变量场双三次曲面拟合(辜旭赞, 2011), 实现球面标、矢量场二阶可导, 以对B网格点(包含极点)做水平平流预报。② 在B网格上, 做水平平流变量和位移纬向三次样条拟合, 从而给全部A网格点赋予“预报”(水平平流和位移)插值。③ 在A网格上, 做“水平平流位移”经向和纬向三次样条拟合, 求出样条格式水平散度场, 以对B网格点做平流增压和绝热增温预报, (并可做气块水汽相变及降水预报)。④ 在B网格上, 做全部水平平流变量垂直三次样条拟合, 从而对B网格点做静力垂直平流预报。⑤ 在B网格上, 再做全部“水平平流+垂直平流”变量纬向三次样条拟合, 以给全部A网格点赋予“预报”插值。
(2) A-J流程(A-J网格切换): ①-⑤ 步骤均同于“A-B流程”, 但将其中的“B网格”通换成“J网格”。
(3) A(B)-J流程(A(B)-J网格切换): ① 在A网格上, 做变量场双三次曲面拟合, 实现球面标、矢量场二阶可导, 以对J网格点(包含极点)做水平平流预报。② 在J网格上, 做水平平流变量和位移纬向三次样条拟合, 以给全部A网格点(包含B网格点)赋予“预报”(水平平流和位移)插值。③、④、⑤ 步骤同于A-B流程。
上述三个流程关键第① 步骤是, 求“B/J网格上游点在A网格上水平坐标”。设某B/J网格点与同纬度最邻近A网格点相距Δx0, 则该上游点在A网格上的水平坐标为(x-Δx0-Δx, y-Δy)。
4.3 Coons双三次曲面与Hermite双三次曲面片球面A网格共有三种拓扑矩形(图 1):一般形(图 1a)、临极点形(图 1b)和极点形(图 1c)。这里是将极点所在的球冠分为4边长准均匀的四个“扇形”(图 1c, 极点不再奇异), 临极点的球带分为1边长为0的“三角形”(图 1b), 其它球带均分为4边长准均匀的“四边形”(图 1a)。
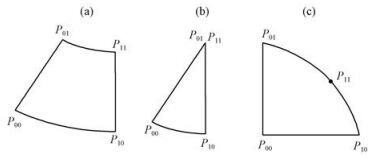
|
图 1 球面A网格上的3种拓扑矩形 (a)一般形, (b)临极点形, (c)极点形. P00、P01、P10、P11为变量值 Figure 1 Three topological rectangular figures of the spherical latitude-longitude grid. (a) general one, (b) one close to the pole, (c) one adjacent to the pole. In Fig. 1, P00, P01, P10 and P11 denote 4 variable values |
在球面A网格上, 可实现各个变量场的Coons双三次曲面拟合(辜旭赞, 2011), 而与球面A网格拓扑矩形一一对应的正好就是Hermite双三次曲面片(Hermite bicubic patch), 因它由4个变量值(设为P00、P01、P10、P11)、8个一阶偏导数(P00x、P01x、P10x、P11x, P00y、P01y、P10y、P11y)和4个二阶混合偏导数(P00xy、P01xy、P10xy、P11xy)完全确定。上游点经过水平“三次运动”路径, 必将落在A网格某一片上。则在各个A网格“二阶可导”变量场上, 既可迭代求得上游点水平坐标, 同时, 又求得上游点全部(预报)变量值。
显然, 容易做“经纬网格-准均匀经纬网格”标、矢量场三次样条函数(双三次曲面)变换, 并实现上述的A-B流程、或A(B)-J流程的准拉格朗日积分方案。
4.4 求上游点以计算准拉格朗日水平平流为例, 设N为北(/南)极点, L(x, y)为经纬网格欧拉预报点, M为上游点(取式(15)、(16)), 并设M水平坐标为(x-Δxn, y-Δyn), n=0, 1, 2, …, 其对应于L的纬向和经向弧度为(Δφn, Δλn), 这时, 需要由初值(Δx0, Δy0)去迭代求得上游点及在“双三次曲面片”上的各个物理量。于是, 求上游点变为求解球面三角形(图 2):已知其“两边一对角”:边β为北(/南)极点至预报点弧长(固定值), 边γ为上游点水平位移弧长, 及∠M, 这里
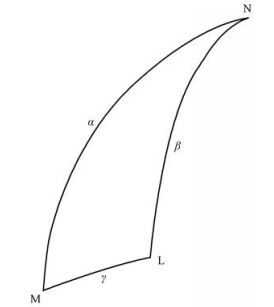
|
图 2 求解球面三角形(求经纬网格上的上游点) N为北(/南)极点, L为经纬网格(预报)点, M为上游点, ∠N, ∠L, ∠M, 边α, 边β(固定值), 边γ(牛顿位移) Figure 2 Solving a upstream point on the spherical triangle. N is the North/South Pole, L is a forecast point on latitude-longitude grid, M is its upstream point, three corners ∠N, ∠L and ∠M, three sides α, β (Fixed value), and γ (Newton's displacement) |
首先实现全球初值模式大气Lorenz大气参考状态(辜旭赞, 2003)。以初值参考大气海平面气压(大于1000 hPa)作为位势高度为零的第0层(底层), 因参考大气满足静力平衡条件, 又以参考气压970 hPa分为第1层, 而从970 hPa到10 hPa, 按每间隔60 hPa分层, 则求出对应于970, 910, 850, …, 70, 10 hPa各层静力位势高度, 它们作为第1~17层, 将参考气压1 hPa位势高度作为第18层(顶层, 表 3), 从而实现准实时、准均匀“质量间隔”垂直坐标。
| 表 3 2008年1月10日14:00(北京时, 下同)初值模式大气参考气压与Z坐标位势高度 Table 3 The geopotential height of Z coordinates and the reference pressure of the atmosphere at the model's initial time of 14:00 (Beijing Time, the same as after) 10 January 2008 |
全球样条模式在水平方向为周期三次样条边界, 但其顶、底层三次样条边界尚值得研究。本文的积分试验, 气压场顶、底层取为“静力”边界, 其它变量场均取为前/后差分边界。
模式顶层可以考虑两种物理边界: (1) 刚盖顶层:设模式顶层无质量、无水汽交换, 但可以有能量净出入, 有
按垂直运动方程式(3), 并设变率aw≡0, 且忽略摩擦力Fw, 则有如下含有压、温、湿、风的“静力平衡方程”:
| $ \frac{{\partial z}}{{\partial \ln p}} = - \frac{{RT}}{{\bar g}}, $ | (39) |
式中:
设模式(分层)高度坐标为Z, 对式(39) 从模式大气底层(用下标s表示)向上直至顶层(用下标“0”表示)作气压差(ps→p→p0)三次样条拟合与积分, 可求得t时刻各层静力位势高度zt(以下在不影响判断时略去上标t):
| $ z = {z_s} + \int_p^{{p_s}} {\frac{{RT}}{g}{\rm{dln}}p} , $ | (40) |
式中: zs为地形高度, 不考虑地形时zs=0。由此诊断求得(Δt)静力水平平流之后各层的垂直位移Δz:
| $ \Delta z = z - Z. $ | (41) |
按“匀加速”预报方程(式(14) 及式(11)), 经整理, 给出各层水平运动预报方程:
| $ {u^{t + \Delta t}} = \ddot u + {{\ddot a}_u}\Delta t - \Delta z{\left( {u + {a_u}\Delta t} \right)^z} + \frac{{{\Delta ^2}z}}{2}{\left( {u + {a_u}\Delta t} \right)^{zz}}, $ | (42) |
| $ {v^{t + \Delta t}} = \ddot v + {{\ddot a}_v}\Delta t - \Delta z{\left( {v + {a_v}\Delta t} \right)^z} + \frac{{{\Delta ^2}z}}{2}{\left( {v + {a_v}\Delta t} \right)^{zz}}, $ | (43) |
式中:
因求水平位移时, 设求经向位移必须满足Courant-Friedrichs-Levy(CFL)计算稳定性条件, 即要求Δy小于一个经距, 而求纬向位移可以突破CFL条件, 但不妨要求Δx也小于一个经距。则设上游点水平风速(u0, v0)=
| $ \left\{ \begin{array}{l} {u_1} = {u_0}\cos \Delta \lambda - {v_0}\sin \Delta \lambda \\ {v_1} = {u_0}\sin \Delta \lambda + {v_0}\cos \Delta \lambda \end{array} \right.,\;\;\;\;\left( {北半球\;0 \le \varphi \le \frac{{\rm{\pi }}}{2}} \right) $ | (44) |
| $ \left\{ \begin{array}{l} {u_1} = {u_0}\cos \Delta \lambda + {v_0}\sin \Delta \lambda \\ {v_1} = - {u_0}\sin \Delta \lambda + {v_0}\cos \Delta \lambda \end{array} \right.,\;\;\;\;\left( {南半球\; - \frac{{\rm{\pi }}}{2} \le \varphi \le 0} \right) $ | (45) |
各层水平运动预报方程变为:
| $ {u^{t + \Delta t}} = {u_1} - \Delta z{\left( {u + {a_u}\Delta t} \right)^z} + \frac{{{\Delta ^2}z}}{2}{\left( {u + {a_u}\Delta t} \right)^{zz}}, $ | (46) |
| $ {v^{t + \Delta t}} = {v_1} - \Delta z{\left( {v + {a_v}\Delta t} \right)^z} + \frac{{{\Delta ^2}z}}{2}{\left( {v + {a_v}\Delta t} \right)^{zz}}, $ | (47) |
因静力方程, 并定义气压变率
| $ \frac{{\partial \omega }}{{\partial p}} + {\left( {\frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}}} \right)_p} - \frac{{v\tan \varphi }}{{{r_0}}} = 0, $ | (48) |
对式(48) 作气压坐标向高度坐标的数学转换。因数学微分
| $ \frac{{\partial \omega }}{{\partial p}} + \frac{{\partial u}}{{\partial x}} - \frac{{\partial u}}{{\partial p}}\frac{{\partial p}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} - \frac{{\partial v}}{{\partial p}}\frac{{\partial p}}{{\partial y}} - \frac{{v\tan \varphi }}{{{r_0}}} = 0, $ | (49) |
对式(49) 定义水平散度
| $ \omega = - \int_{{p_0}}^p {D\left( {u,v} \right){\rm{d}}p} , $ | (50) |
对上式D(u, v)作样条格式时空离散:先求取一个时间步长(Δt)平均水平风速(u, v)≈(u, v)=
| $ \bar \omega \Delta t = - \int_{{p_0}}^{\ddot p\left( Z \right)} {D\left( {\Delta x,\Delta y} \right){\rm{d}}p\hat = \Delta p} , $ | (51) |
式(51)Δp为准拉格朗日静力水平平流增压, 用它可以采用“变加速”预报方程(参见式(22) 及式(16))做增压预报, 从而给出各层的气压预报方程:
| $ \begin{gathered} {p^{t + \Delta t}} = \dddot p + \left( {{\omega ^{t + \Delta t}} + {{\dddot \omega }^t}} \right)\frac{{\Delta t}}{2} \hfill \\ \;\;\;\;\;\;\; \approx \dddot p + \bar \omega \Delta t \hfill \\ \;\;\;\;\;\;\; = \ddot p + \Delta p - \Delta z \cdot {p^z} + \frac{{\Delta {z^2}}}{2}{p^{zz}}, \hfill \\ \end{gathered} $ | (52) |
由式(52) 可知, 显式-准拉格朗日“平均”增压可以代替SI-SL“时间中央差”增压, 但前者相对简单(无须求解Helmholtz方程)。
由式(52) 还得到地面气压预报方程:
| $ p_s^{t + \Delta t} = {{\ddot p}_s} + \Delta {p_s}, $ | (53) |
式(53)Δps为静力平流散度场造成的地面增压(参见式(51), 且做
| $ \Delta {p_s} = - \int_{{p_0}}^{{{\ddot p}_s}} {D\left( {\Delta x,\Delta y} \right){\rm{d}}p} , $ | (54) |
又按热力学方程(参见式(5)), 可由静力增压Δp, 求得准拉格朗日静力水平平流绝热增温
| $ {T^{t + \Delta t}} = \ddot T + \Delta T - \Delta z \cdot {T^z} + \frac{{{\Delta ^2}z}}{2}{T^{zz}}. $ | (55) |
在求出Δp和ΔT之后, 理论上还可以求出气块的水汽变率Δq与显式降水。但本文暂不考虑水汽源汇及相变, 即认为Δq=0, 则给出各层的水汽预报方程:
| $ {q^{t + \Delta t}} = \ddot q - \Delta z \cdot {q^z} + \frac{{{\Delta ^2}z}}{2}{q^{zz}}. $ | (56) |
积分试验表明, 按式(52~53) 做气压场预报, 全球大气质量将出现微弱的波动变化(将(53) 式称为“准守恒”地面气压预报方程), 究其原因, 可能计算Δps时存在垂直积分累积误差。下面推导在显式-准拉格朗日“三维静力平流”(对应式(52~53))基础上的质量守恒地面气压预报方程。
因地面气压变率为(张玉玲等, 1986):
| $ {\omega _s}\hat = \frac{{{\rm{d}}{p_s}}}{{{\rm{d}}t}} = \frac{{\partial {p_s}}}{{\partial t}} + {u_s}\frac{{\partial {p_s}}}{{\partial x}} + {v_s}\frac{{\partial {p_s}}}{{\partial y}}, $ | (57) |
对气压坐标静力连续方程式(48), 经高度坐标静力连续方程式(49) 变换, 其可从模式顶层到底层积分, 实际完成下式(已将式(57) 代入):
| $ \frac{{\partial {p_s}}}{{\partial t}} = - \int_{{p_0}}^{{p_s}} {\left( {\frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} - \frac{{v\tan \varphi }}{{{r_0}}}} \right){\rm{d}}p} - {u_s}\frac{{\partial {p_s}}}{{\partial x}} - {v_s}\frac{{\partial {p_s}}}{{\partial y}}, $ | (58) |
对调式(58) 右边第1项积分与微分次序, 经整理为:
| $ \frac{{\partial {p_s}}}{{\partial t}} = \frac{{ - 1}}{{{r_0}\cos \varphi }}\left( {\frac{\partial }{{\partial \lambda }}\int_{{p_0}}^{{p_s}} {u{\rm{d}}p} + \frac{\partial }{{\partial \varphi }}\int_{{p_0}}^{{p_s}} {v\cos \varphi {\rm{d}}p} } \right), $ | (59) |
式(59) 对全球面积(A)积分, 面积元dA=r02cosφdλdφ, 其右边积分为零, 即:
| $ \int_A {\frac{{\partial {p_s}}}{{\partial t}}{\rm{d}}A} = \frac{\partial }{{\partial t}}\int_A {{p_s}{\rm{d}}A} = 0, $ | (60) |
式(60) 的物理意义是全球大气质量守恒。
可以直接对式(59) 作时空离散化:仍取一个时间步长地面气压平均增量
| $ \frac{{p_s^{t + \Delta t} - p_s^t}}{{\Delta t}} = \frac{{ - 1}}{{{r_0}\cos \varphi }}\left( {\frac{{\partial \tilde u}}{{\partial \lambda }} + \frac{{\partial \tilde v\cos \varphi }}{{\partial \varphi }}} \right) = - \frac{{\partial \tilde u}}{{\partial x}} - \frac{{\partial \tilde v}}{{\partial y}} + \frac{{\tilde v\tan \varphi }}{{{r_0}}}, $ | (61) |
则对已知的
| $ \frac{{p_s^{t + \Delta t} - p_s^t}}{{\Delta t}} = - \frac{{{{\tilde u}^\lambda } + {{\left( {\tilde v\cos \varphi } \right)}^\varphi }}}{{{r_0}\cos \varphi }} = - {{\tilde u}^x} - {{\tilde v}^y} + \frac{{\tilde v\tan \varphi }}{{{r_0}}}, $ | (62) |
利用周期三次样条数学性质, 其“斜率”闭合积分为零, 对上式作全球面积积分, 有:
| $ \int_A {\frac{{p_s^{t + \Delta t} - p_s^t}}{{\Delta t}}{\rm{d}}A} = - \int_A {\left[ {{{\tilde u}^\lambda } + {{\left( {\tilde v\cos \varphi } \right)}^\varphi }} \right]{r_0}{\rm{d}}\lambda {\rm{d}}\varphi } = 0, $ | (63) |
式(63) 右边积分为零(第1项对纬圈积分为零, 第2项对经圈积分为零)。则因式(62), 实际方便采用如下的准拉格朗日全球质量“守恒”地面气压预报方程:
| $ p_s^{t + \Delta t} = p_s^t + \Delta {{\tilde p}_s}\;\;\;\;;\Delta {{\tilde p}_s} = - \Delta t\left( {{{\tilde u}^x} + {{\tilde v}^y} - \frac{{\tilde v\tan \varphi }}{{{r_0}}}} \right), $ | (64) |
又因u~及u~x在极点无定义, 且
| $ \left\{ \begin{array}{l} {\left( {\Delta {{\tilde p}_s}} \right)_N} = - \Delta t\left( {\tilde v_{N\left( {3{\rm{\pi /2}}} \right)}^y + \tilde v_{N\left( 0 \right)}^y} \right)\\ {\left( {\Delta {{\tilde p}_s}} \right)_S} = - \Delta t\left( {\tilde v_{S\left( {{\rm{\pi /2}}} \right)}^y + \tilde v_{S\left( 0 \right)}^y} \right) \end{array} \right.. $ | (65) |
全球样条模式(动力框架), 即高度坐标、无地形、水平1°×1°经纬网格“A网格”及准均匀经纬网格“B网格”和“J网格”(表 2)、垂直19层(表 3), 采用静力守恒样条格式压、温、湿、风预报方程, 条件为干绝热、无摩擦, 且取Δt=180 s。采用NCEP再分析1°×1°资料做初值场, 时间为2008年1月10日14:00和2002年8月19日14:00, 并且做准均匀经纬网格三次样条函数变换A-B流程和A(B)-J流程积分试验, 积分10天(240 h)。
7.1 积分结果分析A-B流程和A(B)-J流程积分结果非常接近(2008年1月10日积分结果见图 3~4, 2002年8月19日积分结果图略), 表明A-B流程积分过程(暂)未发生2倍格距波传播与增长, 即做A网格双三次曲面变换, 求取B网格上游点和J网格上游点在A网格上的水平坐标, 两者基本一致。
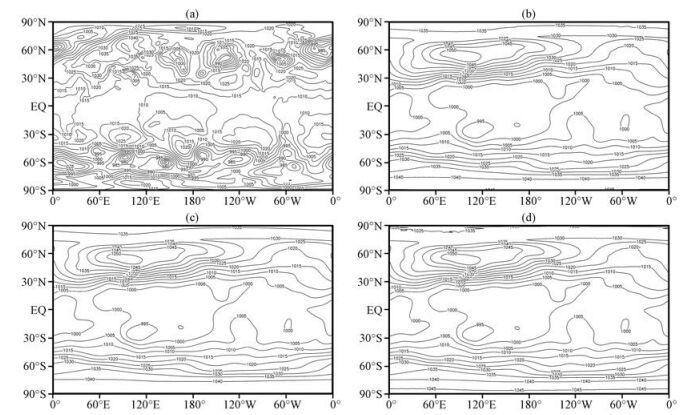
|
图 3 2008年1月10日14:00初始全球地面(海平面)气压场(a), 以及以“lnp”为预报变量, 采用不同流程的“准守恒”与“守恒”积分10天的全球地面(海平面)气压场(单位: hPa) (a)初值场, (b) A(B)-J流程“静力质量守恒”格式, (c) A(B)-J流程“准守恒”格式, (d) A-B流程“静力质量守恒”格式 Figure 3 Initial pressure field at the global sea-level, conserved and quasi-conserved 10 days forecasted global sea-level pressure field applied "lnp" as forecast variable with different procedure at 14:00 on 10 January 2008. Unit: hPa. (a) initial pressure field, (b) conserved forecasted with A(B)-J procedure, (c) quasi-conserved forecasted with A(B)-J procedure, (d) conserved forecasted with A-B procedure |
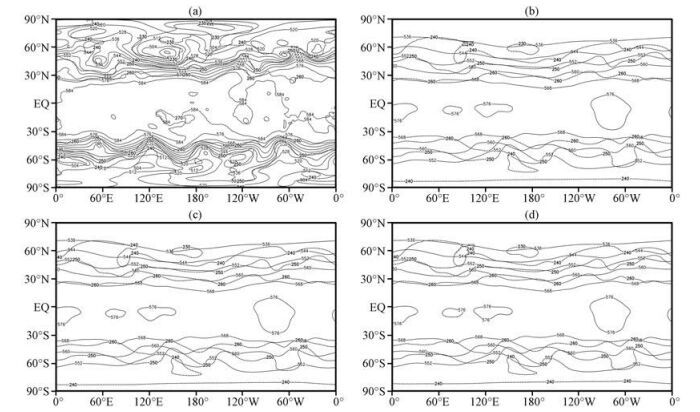
|
图 4 2008年1月10日14:00初始全球500 hPa高度场(实线, 单位: dagpm)和温度场(虚线, 单位: K), 以及以“lnp”为预报变量, 采用不同流程的“准守恒”与“守恒”积分10天全球500 hPa高度场(实线, 单位: dagpm)和温度场(虚线, 单位: K) (a)初值场, (b) A(B)-J流程“静力质量守恒”格式, (c) A(B)-J流程“准守恒”格式, (d) A-B流程“静力质量守恒”格式 Figure 4 Initial global geopotential height field (solid line, unit: dagpm) and temperature field (dotted line, unit: K), conserved and quasi-conserved 10 days forecasted global geopotential height field (solid line, unit: dagpm) and temperature field (dotted line, unit: K) on 500 hPa at 14:00 on 10 January 2008. (a) initial pressure field, (b) conserved forecasted with A(B)-J procedure, (c) quasi-conserved forecasted with A(B)-J procedure, (d) conserved forecasted with A-B procedure |
两个流程“准守恒”与“守恒”积分结果均表明(图 3~4), 准均匀经纬网格三次样条函数变换显式-准拉格朗日积分方案是可行的, 该动力框架描述“(水平)双三次曲面+(垂直)三次样条”三维静力平流, 从初值场到积分10天地面气压场和500 hPa高度场及温度场, 其积分结果有将初值场演变为全球“平均”趋势, 这在理论上是定性正确的。
A(B)-J流程积分结果还表明, “准守恒”与“守恒”积分都考虑了全球三维静力平流, 两者仅地面气压预报方程有“些微”差别, 前者地面气压变率是对各层“质量散度”作气柱积分, 后者是对各层“质通量”作气柱积分之后求其平均散度, 但两者积分10天地面气压场和500 hPa高度场及温度场仍然非常接近(对比图 3和图 4), 表明两者之间可能仅存在微弱的计算累积误差。但“准守恒”积分试验全球大气质量确有微小波动, 总趋势是地面平均气压从2008年1月10日初值为101133. 5 Pa(2002年8月19日初值为101140. 2 Pa)到积分10天的101129. 6 Pa(101139. 4 Pa), 且2008年1月10日地面平均气压最大波动振幅为101133. 5-101126. 7=6. 8 Pa(2002年8月19日为101140. 2-101135. 7=4. 5 Pa), 而“守恒”积分试验, 在绝对误差正负0. 1 Pa范围内, 全球大气质量无变化。另外, A-B流程“准守恒”积分试验地面平均气压有与A(B)-J流程相似的变化, 而其“守恒”积分试验地面平均气压也基本不变。
7.2 “失败”积分结果分析因原始大气运动方程及静力方程(参见式(1)~(4)、(39))允许对“对数气压”(lnp)做预报, 且因微分
若是对气压p(单位: Pa)场做预报, 则发生了A-B流程“失败”积分试验(2008年1月10日“守恒”积分6天结果参见图 5~6, 其它图略)。
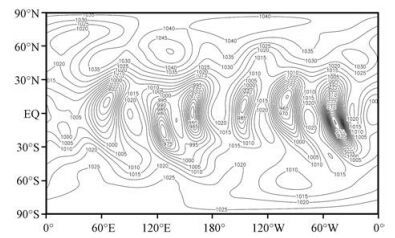
|
图 5 以“p”为预报变量, 采用A-B流程“静力质量守恒”格式积分6天的全球地面(海平面)气压场(单位: hPa) Figure 5 Conserved 6 days forecasted global sea-level pressure field applied "p" as forecast variable with A-B procedure. Unit: hPa |
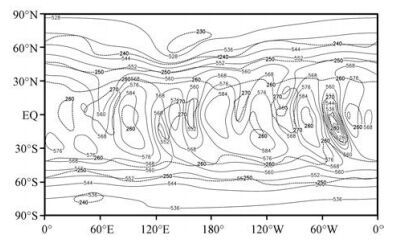
|
图 6 以“p”为预报变量, 采用A-B流程“静力质量守恒”格式积分6天的500 hPa高度场(实线, 单位: dagpm)和温度场(虚线, 单位: K) Figure 6 Conserved 6 days forecasted global geopotential height field (solidline, unit: dagpm) and temperature field (dotted line, unit: K) at 500 hPa applied "p" as forecast variable with A-B procedure |
究其原因(表 2), 可能是在B网格59°S/59°N做间隔1°纬距的360个点预报, 而在相邻60°S/60°N变为做间隔2°纬距的180个点预报, 另外的180个点为三次样条(内)插值, 形成二倍格距过渡界线, 从而造成在60°S/60°N的预报截断误差及相速、群速误差, 均为在59°S/59°N的两倍。故这里最容易出现虚假寄生波, 且当寄生波向短波发展时, 二倍格距过渡界线两侧截断误差及相速、群速误差迅速增长, 且两侧差别越来越大, 则是样条格式“预报”寄生波在这里发展并进入到中-低纬带, 寄生波随能量频散向上游方向发展, 但向下游方向传播, “守恒”和“准守恒”积分试验都发生了寄生波“气旋”与“反气旋”传播与增长(图 5~6)。最后, 可能因所谓“非线性混淆误差”, “守恒”和“准守恒”积分试验都出现计算不稳定, 即都发生对气压p场(不是lnp场)作三次样条拟合之尖点或环绕(拟合失败), 尽管在积分不稳定出现之前, “守恒”积分试验的大气质量仍然保持不变。
显然, 在A-B/A(B)-J/A-J网格上, lnp场与p场样条格式拟合斜率、曲率和挠率存在一定差别(前者较为平缓), 且是A-B网格(存在二倍格距过渡界线)促成了“失败”模拟结果。
8 结论(1) 样条格式是关于全部格点的二阶可导非线性格式, 但样条格式线性部分是二阶中央差。本文在给定简谐波真解条件下, 推导证明二阶中央差比一阶中央差空间截断误差及相速和群速误差均减少一倍, 但两种格式相速和群速均与波数有关, 将真解非频散波拟合成为频散波, 且两种格式均为“群速慢于相速慢于真实气流”(能量逆向频散快于位相逆向传播), 波长越短, 误差越大, 这使得在扰动上游产生新的波动、或使得原有的波动增强, 出现上游/下游(向下游传播)效应, 这一方面对于预报天气系统移动、新生很重要, 另一方面也可能导致出现虚假“寄生(短)波”, 寄生波在基本气流上游逐渐形成, 并向下游传播, 寄生波发展可能造成某一变量场的计算紊乱, 但非线性样条格式的真实情况有待进一步(做理想场试验)研究。
(2) 与谱模式数学基础相当, 三次样条函数具备对于原函数及其1阶、2阶导数“收敛性”和对于原函数二阶导数最佳逼近“最优性”及“周期性”, 适合做全球/区域统一数值模式, 从而对应于谱模式动力框架核心, “高斯网格二维谱变换半隐式-半拉格朗日积分方案”, 本文提出样条模式动力框架核心, “准均匀经纬网格三次样条函数变换显式-准拉格朗日积分方案”。
(3) 给出准拉格朗日样条格式预报方程通式, 做“水平双三次曲面+垂直三次样条”拟合以求二阶时空精度上游点运动路径, 将广义牛顿力整体作为“匀加速”变率做风场预报, 以求一个时间步长水平位移以及“平均”散度场, 当作“变加速”变率做增压与增温(及水汽相变)预报, 从而实现全球静力守恒准均匀经纬网格样条格式数值模式, (而采用“三次曲体”拟合求上游点可做非静力数值模式), 这时, 气块的“三次运动路径”包含了“斜率”平流、“曲率”弯流和“挠率”扭流。风场预报(只)可以采用“匀加速”方案, 以避免采用半隐式-半拉格朗日积分方案, 进而避免求解Helmholtz方程, 而压、温(湿)场预报可采用计算精度较高的“变加速”方案, 因其变率就是“匀加速”方案已做预报的风场(位移)散度, 故整个“显式+隐式”方案, 本质上仍只是显式方案。
(4) 在球面经纬网格(A网格)基础上, 设计两种基本的准均匀经纬网格: B网格和J网格, 其中B网格点与A网格点重合, 但不可避免存在2倍格距过渡界线, 容易造成虚假的寄生(短)波传播与增长; J网格避免出现2倍格距过渡界线, 且J网格点一般不与A网格点重合。理论上还可设计多种准均匀经纬网格, 例如, 通过做“A网格-高斯网格”三次样条函数变换, 并通过做理想积分试验, 将来可与谱模式动力框架去比较计算精度。
(5) 做“A-B”网格三次样条函数变换积分试验, 若对对数气压(lnp)场做样条格式变换, 则没有发生虚假寄生波, 而若对气压(p)场做样条格式变换, 则出现明显的虚假寄生波传播与增长模拟个例, 发生这种现象, 是因为在A-B/A(B)-J/A-J网格上, lnp场与p场样条格式拟合斜率、曲率和挠率存在差别(可以肯定后者斜率较大), 其中A-B网格存在2倍格距过渡界线, 其一侧截断误差及相速、群速误差为另一侧的两倍, 从而促成了“失败”的模拟结果, 解决积分不稳定的方法有:在各种网格上做变量场平滑或样条格式光顺, 但平滑是“以精度换稳定”, 故将来应研究“准均匀(变)经纬网格”。
(6) 积分试验证明, 可设计出全球静力守恒样条格式准拉格朗日积分方案, 其做法是引入高度坐标静力连续方程, 其算法是直接对静力水平平流“位移”求样条格式散度场。
(7) 将来全球样条模式宜引入具有定常斜率、曲率和挠率的双三次曲面地形与地形追随高度坐标。
| Layton A T. 2002. Cubic spline collocation method for the shallow water equations on the sphere[J]. Journal of Computational Physics, 179(2): 578–592. DOI:10.1006/jcph.2002.7075 | |
| Bubnová R, Hello G, Bénard P, et al. 1995. Integration of the fully elastic equations cast in the hydrostatic pressure terrain-following coordinate in the framework of the ARPEGE/Aladin NWP system[J]. Mon Wea Rev, 123(2): 515–535. DOI:10.1175/1520-0493(1995)123<0515:IOTFEE>2.0.CO;2 | |
| Côté J, Gravel S, Méthot A, et al. 1998a. The operational CMC-MRB global environmental multiscale (GEM) model. Part Ⅰ:Design considerations and formulation[J]. Mon Wea Rev, 126(6): 1373–1395. DOI:10.1175/1520-0493(1998)126<1373:TOCMGE>2.0.CO;2 | |
| Côté J, Desmarais J G, Gravel S, et al. 1998b. The operational CMC|MRB global environmental multiscale (GEM) model. Part Ⅱ:results[J]. Mon Wea Rev, 126(6): 1397–1418. DOI:10.1175/1520-0493(1998)126<1397:TOCMGE>2.0.CO;2 | |
| Cullen M J P. 1990. A test of a semi-implicit integration technique for a fully compressible non-hydrostatic model[J]. Quart J Roy Meteor Soc, 116(495): 1253–1258. DOI:10.1002/(ISSN)1477-870X | |
| Cullen M J P, Davies T, Mawson M H, et al. 1997. An overview of numerical methods for the next generation UK NWP and climate model[J]. Atmos-Ocean, 35(supp1): 425–444. | |
| Ferguson J. 1964. Multivariable curve interpolation[J]. Journal of the ACM (JACM), 11(2): 221–228. DOI:10.1145/321217.321225 | |
| Gal-Chen T, Somerville R C J. 1975. On the use of a coordinate transformation for the solution of the Navier-Stokes equations[J]. Journal of Computational Physics, 17(2): 209–228. DOI:10.1016/0021-9991(75)90037-6 | |
| Li X, Chen D, Peng X, et al. 2006. Implementation of the semi-Lagrangian advection scheme on a quasi-uniform overset grid on a sphere[J]. Adv Atmos Sci, 23(5): 792–801. DOI:10.1007/s00376-006-0792-9 | |
| McDonald A, Bates J R. 1989. Semi-Lagrangian integration of a gridpoint shallow water model on the sphere[J]. Mon Wea Rev, 117(1): 130–137. DOI:10.1175/1520-0493(1989)117<0130:SLIOAG>2.0.CO;2 | |
| Ritchie H, Beaudoin C. 1994. Approximations and sensitivity experiments with a baroclinic semi-Lagrangian spectral model[J]. Mon Wea Rev, 122(10): 2391–2399. DOI:10.1175/1520-0493(1994)122<2391:AASEWA>2.0.CO;2 | |
| 陈德辉, 胡志晋, 徐大海, 等. 2004. CAMS大气数值预报模式系统研究[M]. 北京: 气象出版社, 190. Chen Dehui, Hu Zhijing, Xu Dahai, et al. 2004. Research on the system of atmospheric numerical prediction model (CAMS)[M]. Beijing: China Meteorological Press, 190. | |
| 辜旭赞. 2003. 一模式大气参考状态的科学计算与特征分析[J]. 高原气象, 22(6): 608–612. Gu Xuzan. 2003. Compution and characteristic of a model atmospheric reference state[J]. Plateau Meteor, 22(6): 608–612. | |
| 辜旭赞. 2010. "准拉格朗日法"和"欧拉法"数学一致性与三次插值函数算法时间积分方案[J]. 高原气象, 29(3): 655–661. Gu Xuzan. 2010. The mathematical consistency of quasi-Lagrangian and Eulerian time integratifmn schemes with fitting ciibic interpolation functifmn[J]. Plateau Meteor, 29(3): 655–661. | |
| 辜旭赞. 2011. 一种"准拉格朗日法"和"欧拉法"统一算法时间积分方案[J]. 气象学报, 69(3): 440–446. DOI:10.11676/qxxb2011.038 Gu Xuzan. 2011. A new quasi-Lagrangian time integration scheme with the interpolation of fitting bicubic surface[J]. Acta Meteor Sinica, 69(3): 440–446. DOI:10.11676/qxxb2011.038 | |
| 李江浩, 彭新东. 2013. 阴阳网格上质量守恒计算性能分析[J]. 大气科学, 37(4): 852–862. DOI:10.3878/j.issn.1006-9895.2012.12060 Li Jianghao, Peng Xindong. 2013. Analysis of computational performance of conservative constraint on the Yin-Yang Grid[J]. Chinese J Atmos Sci, 37(4): 852–862. DOI:10.3878/j.issn.1006-9895.2012.12060 | |
| 廖洞贤. 1999. 大气数值模式的设计[M]. 北京: 气象出版社, 291. Liao Dongxian. 1999. Design of atmospheric numerical model[M]. Beijing: China Meteorological Press, 291. | |
| 吕美仲, 欧阳子济, 翟子航. 1983. 正压原始方程半隐式样条格式[J]. 气象科学, 4(2): 1–11. Lü Meizhong, Ouyang Ziji, Zhai Zihang. 1983. The semi-implicit spline scheme of the barotropic primitive equation[J]. J Meteor Sci, 4(2): 1–11. | |
| 奚梅成. 1995. 数值分析方法[M]. 合肥: 中国科学技术大学出版社, 377. Xi Meicheng. 1995. Numerical analysis method[M]. Hefei: University of Science & Technology China Press, 377. | |
| 薛纪善, 陈德辉. 2008. 数值预报系统GRAPES的科学设计与应用[M]. 北京: 科学出版社, 383. Xue Jishan, Chen Dehui. 2008. Scientific design and application of the numerical prediction system (GRAPES)[M]. Beijing: Science Press, 383. | |
| 张玉玲, 吴辉碇, 王晓林. 1986. 数值天气预报[M]. 北京: 科学出版社, 472. Zhang Yulin, Wu Huizhan, Wang Xiaolin. 1986. Numerical weather Prediction[M]. Beijing: Science Press, 472. | |
| 周毅, 刘宇迪, 桂祁军, 等. 2002. 现代数值天气预报[M]. 北京: 气象出版社, 220. Zhou Yi, Liu Yudi, Gui Qijun, et al. 2002. Modern numerical weather prediction[M]. Beijing: China Meteorological Press, 220. |
2. Institute of Ocean Science and Engineering, National University of Defence Technology, Changsha 410073, China
 2017, Vol. 36
2017, Vol. 36
