2. 中国气象局公共气象服务中心, 北京 100081;
3. 中国气象局风能太阳能资源中心, 北京 100081
雾霾污染的有效治理及减排承诺提前完成的现实需求促使能源革命加速推进, 太阳能发电产业也得到迅速发展。与太阳能发电相关的“太阳能辐照度-光伏组件-逆变器-损耗”的一系列模型系统的仿真和决策优化设计均以各地典型气象年数据为基础, 可见, 典型气象年数据的选取不仅对区域太阳能资源评估与区划结果的科学代表性具有重要意义(王炳忠等, 1980; 申彦波等, 2010, 2015; 谷晓平等, 2009; 朱飙等, 2010; 刘可群等, 2007; 周扬等, 2010; 郑有飞等, 2012; 辛渝等, 2011), 同时也对光伏发电系统的优化设计至关重要(白建波等, 2014)。已有研究大多采用气候平均方法对长序列的辐射数据进行分析(朱飙等, 2010; 刘可群等, 2007; 周扬等, 2010), 用来代表该区域或该时间段内的典型特征。
由于太阳能资源评估缺少详细的技术规范, 目前基于长期辐射序列获取典型气象年辐射资料的方法除上述的气候平均法之外, 频率(数)最大法也在光伏电站资源评估中有了初步的应用。这两种算法均具有明确的数学统计意义, 但在典型天气形势的刻画方面不具有代表性。因此, 太阳能资源评估领域中需要进一步提出切实可行的、能较好地代表评估区域长期气候特征的典型年辐射数据计算方法, 以有效提高太阳能资源评估结果的科学代表性。上述需求使得典型气象年算法在太阳能资源评估领域中的应用成为可能。
典型气象年资料的研究最早始于20世纪70年代, 跟随计算机的发展而发展(杨柳等, 2006)。在1978年美国Sandia国家实验室提出挑选典型气象年的基本方法后, 欧美及日本各国相继建立了由实测数据加工而成的气象数据库(Hall et al, 1978; Marion et al, 1995; Wilox et al, 2007, 2008), 由于Sandia方法可挑选出长序列气象数据中具有气候特征代表性的典型月份和典型年资料, 使典型气象年生成方法在能源相关领域中受到学者的优先推荐(Crawley, 1998), 同时也促进了大气环境模拟技术的不断发展。虽然Sandia方法经过了不同程度的发展(Feuermann et al, 1985; Pissimanis et al, 1988; Festa et al, 1993; Lam et al, 1996; Janjai et al, 2009), 但其核心技术仍然保持了Sandia国家实验室最初使用的Finkelstein-Schafer统计方法, 即通过对比所选月份的逐年累积分布函数与长期累积分布函数的接近程度, 进而挑选出12个均具有代表性的典型月组成一个理想气象年。中国学者也开展了相关研究工作, 在建筑节能行业基础数据库的完善(杨柳等, 2006; 李红莲等, 2015)、建筑能耗动态模拟气象资料的推算(顾骏强等, 2008)等方面取得了初步的应用成果, 但在其他行业尤其是对典型气象年辐射资料要求较高的光伏发电行业, Sandia方法的应用非常有限。
因此, 首先尝试利用Finkelstein-Schafer统计方法, 综合考虑影响待评估区域大气环境状况的太阳辐射、气温、相对湿度、风速、气压以及露点温度等气象观测资料, 利用Sandia方法进行典型气象年辐射资料的挑选; 在此基础上, 将Sandia方法与太阳能资源评估中常用的两种典型年挑选方法进行对比, 分析三种方法的应用特点, 进而为太阳能资源的科学评估提供合理客观的依据。
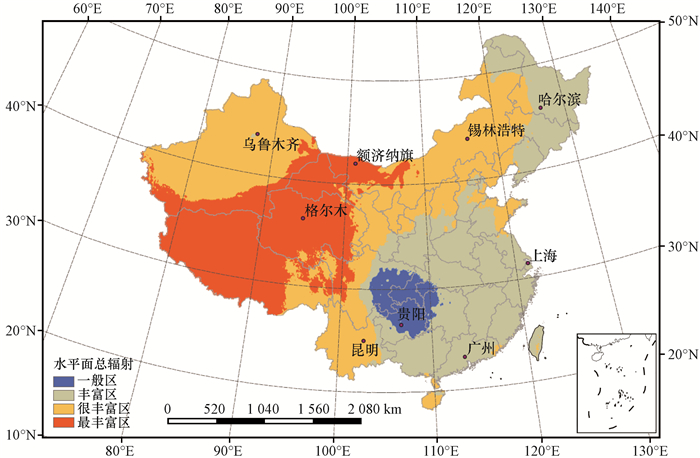
2 代表站点选择、数据与方法 2.1 代表站点选择我国幅员广大, 有着十分丰富的太阳能资源, 为反映我国太阳能资源开发利用典型地区的特点, 参考申彦波等(2016)挑选代表性辐射观测站的原则: (1)兼顾所有太阳能资源等级区域, 重点考虑资源丰富区; (2)空间分布上尽可能均匀, 兼顾行政区; (3)综合考虑地形、气候特征及辐射站的观测环境、建站和迁站情况等。选择全国范围内的9个代表辐射站, 开展三种典型年挑选方法的适用性对比分析, 其中太阳能资源Ⅰ类最丰富区的代表站包括格尔木和额济纳旗; Ⅱ类很丰富区的代表站包括乌鲁木齐、昆明和锡林浩特; Ⅲ类丰富区的代表站包括上海、广州和哈尔滨; Ⅳ类一般区的代表站以贵阳为例(图 1)。
|
图 1 研究选取的9个代表站点分布 Figure 1 Distribution of the nine typical stations used in this study |
由国家气象信息中心提供的全国辐射站点近30年(1985-2014年)逐日平均的空气温度、相对湿度、风速和水平面总辐射曝辐量, 其中空气温度包括最大值、最小值和平均值, 风速包括平均风速和最大风速。
为更好地描述大气环境特征以满足研究中典型气象年挑选法的需求, 利用收集到的基础气象观测资料, 通过式(1)~(3)计算得到日平均露点温度:
| $ {T_d} = \frac{b}{{\frac{a}{{\log \left({\frac{e}{{6.11}}} \right)}} - 1}}, $ | (1) |
| $ e = f \times {E_s}, $ | (2) |
| $ {E_s} = {E_0} \times {10^{\left({\frac{{a \times t}}{{b + t}}} \right)}}, $ | (3) |
式中: Td为空气露点温度(单位: ℃); e为空气的水汽压(单位: hPa); a, b为经验参数, 当t>0 ℃时, a=7.5, b=237.3;当t≤0 ℃时, a=9.5, b=265.5; f为空气的相对湿度(单位: %); Es为空气的饱和水汽压(单位: hPa); E0为空气温度为0 ℃时的饱和水汽压, 取E0=6.11 hPa; t为空气温度(单位: ℃)。
2.3 方法简介 2.3.1 基于正态拟合的概率最大法正态分布是应用最为广泛的连续概率分布, 也称为高斯分布, 适用于正态或近似正态分布的资料, 其特征为“钟”形曲线, 这种分布的概率密度函数为:
| $ f(x) = \frac{1}{{\sqrt {2{\rm{ \mathit{ π} }}} \sigma }}{e^{ - \frac{{{{(x - \mu)}^2}}}{{2{\sigma ^2}}}}}, - \infty < x < \infty $ | (4) |
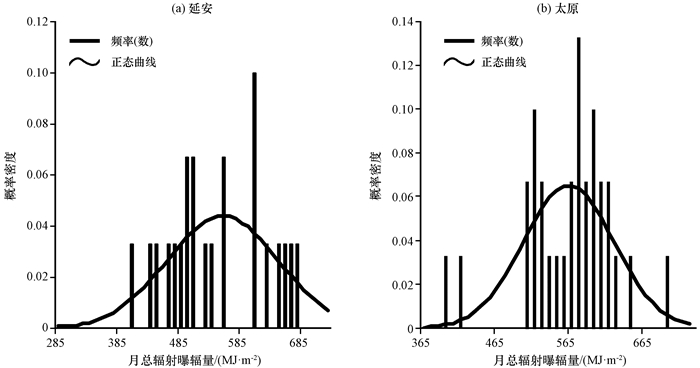
式中有两个参数, 即均数μ和标准差σ, 均数μ决定正态曲线的中心位置; 标准差σ决定正态曲线的陡峭或者扁平程度, 这里随机选取延安和太原为例, 对正态拟合概率密度法进行说明, 如图 2黑色曲线所示。
|
图 2 1985-2014年逐年6月延安(a)和太原(b)总辐射量的正态拟合概率密度曲线和频率直方图 Figure 2 Potential density distributions of global radiation observed at Yan'an (a) and Taiyuan (b) in June from 1985 to 2014 |
以固定间隔Δx为划分, 分别计算序列Y(N)落在取值间隔(Xi, Xi+Δx)内的样本个数Ni, 则该间隔内的频率Pi=Ni/N, 该频率越大, 则代表序列Y(N)在此间隔内的样本数越多(图 2)。
图 2(a)高斯分布的中心位置(最大概率)对应的月总辐射曝辐量为555 MJ·m-2, 而频率(数)最大值对应的月总辐射曝辐量为605 MJ·m-2, 差距较大; 图 2(b)中高斯分布的最大概率和频率最大值对应的月总辐射曝辐量分别为560 MJ·m-2和575 MJ·m-2, 比较接近, 说明当序列的频率直方图较好地符合高斯分布特征时, 上述两种概率最大值挑选的典型月总辐射曝辐量比较接近; 反之则具有一定差异。
根据高斯概率密度函数的性质可知, 高斯概率密度的峰值对应于序列的算术平均值。综上所述, 通过长序列平均, 即正态拟合法获取的典型年资料与通过频率(数)峰值获取的典型年资料的统计指示意义不同。
2.3.3 Sandia国家实验室法由美国Sandia国家实验室提出的典型气象年选取方法, 首先采用Finkelstein-Schafer统计算法, 通过对比所选月份的逐年累积分布函数与长期累积分布函数的接近程度, 挑选出12个均具有代表性的典型月组成一个理想气象年。而典型月的选取需要考虑各个气象要素在大气环境中所占的权重, 被分析的气象要素应尽可能代表大气环境的整体变化特征, 且相互独立。因此被分析的气象要素包括气温、露点温度、风速和水平面总辐射等。主要根据以下步骤实现典型年资料的挑选:
(1) 计算各个气象要素分布的长期累积分布函数值和逐年月累积分布函数值。首先对历年该气象要素按增序排列, 这里的样本数为30年(1985-2014年)乘以月份具有的天数(如1月样本数n为30×31=930)。按式(5)计算该要素的累积分布函数值:
| $ {S_n}(x) = \frac{{k - 0.5}}{n}, $ | (5) |
式中: Sn(x)为x处的长期累积分布值; n为样本总数; k为要素x在增序时间序列中的排序。然后, 按照年份顺序分别在目标月份内按照增序排列, 再按式(5)计算该要素逐年的月累积分布值。
(2) 对每个气象要素的分布计算其Finkelstein-Schafer统计值(Cfs), 即:
| $ {C_{fs}} = \frac{{\sum\limits_{i = 1}^{nd} {{\delta _i}} }}{{nd}}, $ | (6) |
式中: δi为各要素长期累积分布值与逐年各月累积分布值的绝对差值; nd为各分析月内的天数。在获得各气象要素每个月份的Cfs后, 按一定权重系数WFi把各Cfs汇总成一个参数WS, 该系数代表了各气象要素在大气环境中的作用比重。由于缺乏这方面的试验观测和分析数据, 这里综合考虑收集到的基础气象资料及相关研究中露点温度的日变化特征(李昀英等, 2003), 对杨柳等(2006)研究中的各气象要素权重系数进行局部修正, 即合并露点温度的权重(表 1), 给出气象要素对太阳能电站大气环境分析的综合指数Ws:
| 表 1 生成典型气象月各构成气象要素的权重系数WF Table 1 Weighting factors assigned for the respective weather indices |
| $ {W_s} = \sum\limits_{i = 1}^{KK} {{W_{Fi}} \times {C_{fsi}}}, $ | (7) |
式中:KK为气象要素的个数, 取值为7。
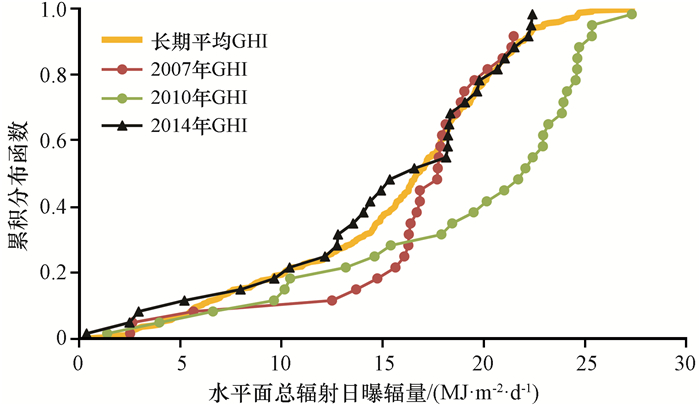
由式(7)可见, Ws越小, 其结果就越接近长期平均值。以单一要素水平面总辐射曝辐量(Global Horizontal Irradiations, GHI)为例, 对比分析兰州辐射站在三个代表年(2007, 2010和2014年)9月份逐日观测GHI的累积分布曲线与该站点近30年(1985-2014年)9月份GHI的长期累积分布曲线(图 3)可以看出, 2010年9月的辐射分布特征与长期累积分布曲线偏离最大, 而2014年9月的辐射分布特征与长期累积分布曲线最接近, 即对应的Cfs最小。依次计算9月份其他气象要素的Cfs后, 根据表 1中的权重系数计算逐年9月份的Ws值, 选取Ws最小值所在年份为9月典型月的年份, 以此类推, 选取其他11个月的典型月, 最终组合构成典型年, 并形成相应的气象数据集。
|
图 3 兰州站3个代表站年9月份水平面总辐射曝辐量(GHI)的累积分布函数与长期累积分布函数(1985-2014年)的对比 Figure 3 Comparison of the cumulative distribution functions (CDF) for September and the long-term (1985-2014) global horizontal solar radiation (GHI) observed |
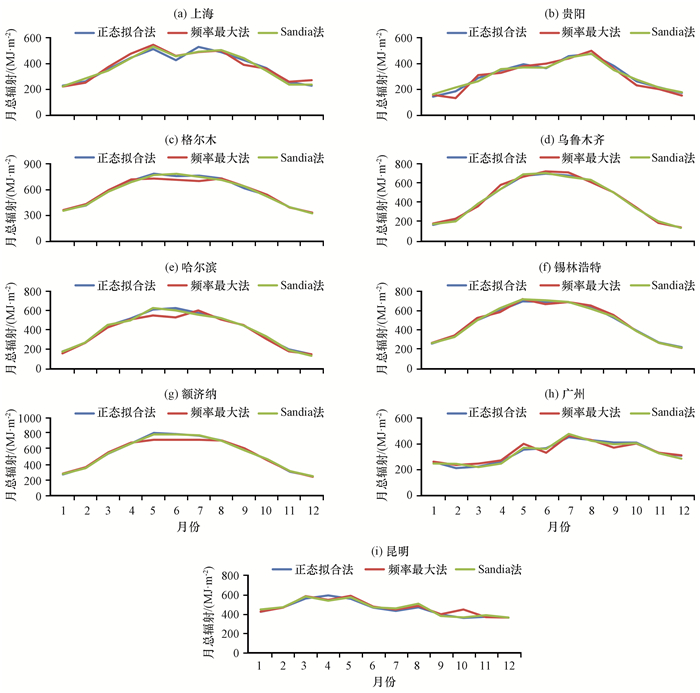
按照2.3所述三种方法, 根据1985-2014年的逐日气象观测资料, 分别计算9个代表站点典型年的水平面年总辐射曝辐量(GHI)。由于正态法是最便捷、工程应用最广泛的方法, 且实际中又不能获取所谓的“真值”, 因此, 以正态法作为参照, 对几种不同的挑选方法进行比较。结果显示, Sandia法得到的GHI量值与正态拟合法获取的GHI量值比较接近, 相对误差基本介于±1.0%之间; 而频率最大法获取的GHI量值偏差比较大, 相对误差基本都超过±1.3%, 有的站点偏差甚至超过4%(表 2)。9个代表站逐月水平面总辐射曝辐量的对比结果中, 频率最大法与其他两种方法之间同样表现出较大的偏离(图 4), 因此在之后的分析中, 重点对比分析正态拟合法与Sandia法之间的特点。
|
图 4 三种算法获取的9个代表站典型年水平面月总辐射曝辐量 Figure 4 Monthly GHI obtained from the three different generating methods of typical year at the nine stations |
| 表 2 三种典型年算法获取的9个代表站水平面年总辐射曝辐量 Table 2 Annual mean global horizontal radiations obtained from the three methods of typical meteorological year at the nine stations |
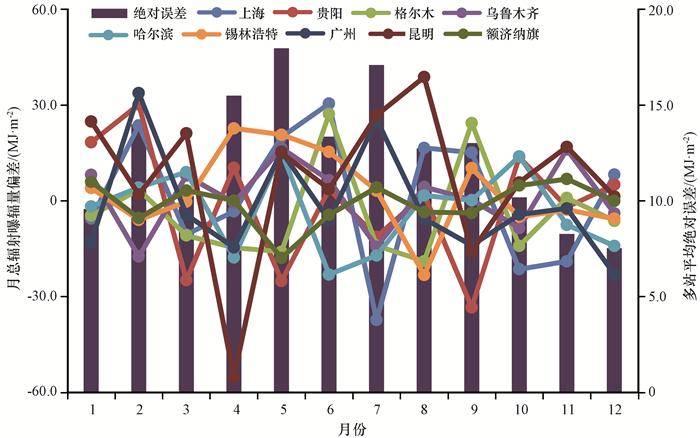
尽管Sandia法(前者)与正态拟合法(后者)获取的年总辐射曝辐量差异较小(表 2), 但从两者逐月辐射曝辐量的对比来看, 则存在较大的波动性:对每一个代表站点来说, 有些月份前者曝辐量高于后者, 有些月份则相反, 尤其是天气特征复杂多变的昆明、贵阳和上海站(图 5曲线)。平均而言, 差异较大的月份集中在4月、5月和7月(图 5柱状), 即天气复杂多变的春夏季。
|
图 5 各代表站点Sandia法与正态拟合法计算的月总辐射曝辐量的偏差及两者绝对误差的多站点平均误差 Figure 5 Monthly mean GHI bias between the normal distribution and Sandia method as well as the monthly absolute error between these two methods averaged over the nine stations |
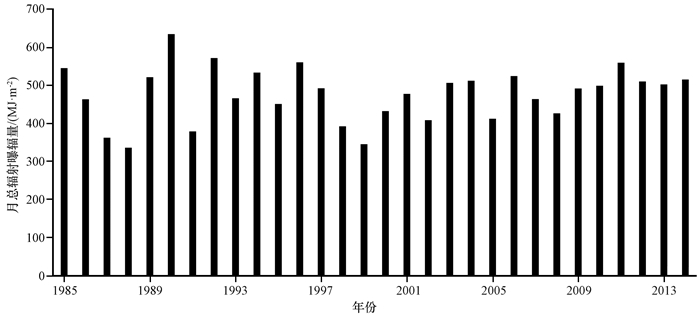
为进一步说明Sandia法与正态拟合法的差异, 图 6给出了昆明站近30年(1985-2014年)8月份的月总辐射曝辐量的变化, 可以看出近30年8月平均的月总辐射曝辐量变化波动性较大:最大值出现在1990年, 月总辐射曝辐量为635.7 MJ·m-2; 最小值出现在1988年, 月总辐射曝辐量为336.7 MJ·m-2。气象观测显示, 昆明地区近30年8月平均的月平均降水量为188.7 mm(最大值为375.4 mm, 最小值为57.2 mm), 月平均降水日数为18.1天(最大值为27天, 最小值为8天), 最长连续降水日数超过7天, 总云量大于8成的天数超过20天(最大值为26天, 最小值为8天)。可见, 昆明地区8月份的天气复杂多变, 造成了该地区月总辐射曝辐量的较大波动。对于图 6所示的月总辐射曝辐量, 基于正态拟合法得到的典型月总辐射曝辐量为477.4 MJ·m-2, 而利用Sandia法获取的典型月总辐射曝辐量为516.1 MJ·m-2。由于正态拟合法获取的多年平均量值的气候代表性不足; 而Sandia法考虑了气象要素的综合变化特征, 代表了典型大气环境的演变特点, 因此最终导致两种算法在复杂天气时段存在较大的差异。上述分析表明两种算法之间的差异波动性受到天气特征的影响, 天气条件越复杂, 两者的差异越明显。
|
图 6 1985-2014年8月昆明站逐月总辐射曝辐量的变化 Figure 6 Inter-annual variation of the monthly global horizontal radiations observed in Kunming at August from 1985 to 2014 |
利用近30年逐日总辐射曝辐量、风速、气温、湿度和露点等地面观测资料, 通过FS统计分析方法, 对全国9个代表站点逐月的气象条件与多年平均气象条件进行相似分析, 进而构建了适用于太阳能资源评估的典型年挑选方法, 主要得到以下结论:
(1) 基于Sandia法挑选的典型年水平面年总辐射曝辐量与近30年平均值, 即正态拟合法的计算结果接近, 两者的相对误差介于±1.0%之间, 而频率最大法则偏离较大。
(2) 典型年水平面总辐射曝辐量的逐月对比显示, 基于Sandia法获取的逐月总辐射曝辐量与近30年平均值之间的差值存在较明显的波动, 即有些月份前者月曝辐量高于后者, 有些月份则相反; 进一步研究表明, 这种波动与天气复杂程度有关。
(3) Sandia法综合反映了气象要素的整体变化特征, 体现了典型大气环境的综合特点, 具有较强的科学代表性, 但在应用中需要大量气象观测数据的支撑。同时, Sandia法挑选的数据代表典型而非极端情况, 并不适用于极端条件下的系统设计。
(4) 正态拟合法在典型年的挑选过程中仅引入太阳辐射曝辐量的观测值, 便于快速有效地应用, 但所选典型年缺少气候代表性。
通过太阳能资源评估典型年挑选方法的对比分析, 为太阳能资源的科学评估提供了参考依据。但太阳能资源评估是一个复杂有难度的工作, 任何评估方法都存在缺陷和不足。对于太阳能资源评估而言, 需要紧密结合生产生活实际, 不断开展相关理论和技术方法的研究, 提高技术服务水平。
Crawley D B. 1998. Which weather data should you use for energy simulations of commercial buildings?[J]. ASHRAE Trans, 104: 498–515.
|
|
Festa R, Ratto C F. 1993. Proposal of a numerical procedure to select reference years[J]. Sol Energy, 50: 9–17.
DOI:10.1016/0038-092X(93)90003-7 |
|
Feuermann D, Gordon J M, Zarmi Y. 1985. A typical meteorological day "TMY" approach for predicting the long-term performance of solar energy systems[J]. J Sol Energy, 35: 499–507.
|
|
Hall I, Prairie R, Anderson H, et al, 1978. Generation of typical meteorological years for 26 SOLMET stations[R]. SAND78-1601. Albuquerque, NM:Sandia National Laboratories.
|
|
Janjai S, Deeyai P. 2009. Comparison of methods for generating typical meteorological year using meteorological data from a tropical environment[J]. Appl Energy, 86: 528–537.
DOI:10.1016/j.apenergy.2008.08.008 |
|
Lam J C, Hui S C M, Chan A L S. 1996. A statistical approach to the development of a typical meteorological year for Hong Kong[J]. Architect Sci Rev, 39: 201–219.
DOI:10.1080/00038628.1996.9696818 |
|
Marion W, Urban K, 1995. User's manual for TMY2s-typical meteorological years derived from the 1961-1990 national solar radiation data base[M]. Golden, CO:National Renewable Energy Laboratory, 1-55.
|
|
Pissimanis D, Karras G, Notaridou V, et al. 1988. The generation of a "typical Meteorological Year" for the city of Athens[J]. J Sol Energy, 40: 405–411.
DOI:10.1016/0038-092X(88)90095-3 |
|
Wilox S, Marion W, 2008. User's manual for TMY3 data sets[R]. NREL Report No. TP-581-41356, 50.
|
|
Wilox S, 2007. National solar radiation database 1991-2005 update:User's Manual[R]. NREL Report No. TP-581-41364, 472.
|
|
白建波, 曹阳, 郝玉哲, 等. 2014. 光伏并网电站仿真与决策优化软件设计[J]. 太阳能能学报, 34(10): 2022–2029.
Bai J B, Cao Y, Hao Y Z, et al. 2014. Development of simulation and decision-makings of software of solar PV grid-connected power system[J]. Acta Energiae Solaris Sinica, 34(10): 2022–2029.
|
|
谷晓平, 袁淑杰, 史岚, 等. 2009. 基于DEM的复杂地形下太阳散散射辐射分布式模式——以贵州高原为例[J]. 高原气象, 28(1): 143–150.
Gu X P, Yuan S J, Shi L, et al. 2009. Study on distributed simulation of diffuse solar radiation over complex terrains based on DEM-taking Guizhou Plateau for example[J]. Plateau Meteor, 28(1): 143–150.
|
|
顾骏强, 杨军, 陈海燕, 等. 2008. 建筑能耗动态模拟气象资料的开发与应用[J]. 太阳能学报, 29(1): 119–124.
Gu J Q, Yang J, Chen H Y, et al. 2008. Development and application of meteorological data on dynamically modeling of energy consumption in dwelling buildings[J]. Acta Energlae Solaris Sinca, 29(1): 119–124.
|
|
李红莲, 杨柳, 刘大龙, 等. 2015. 建筑能耗模拟用典型气象年产生方法的研究[J]. 西安建筑科技大学学报(自然科学版), 47(2): 267–271.
Li H L, Yang L, Liu D L, et al. 2015. Research on the method of generate TMY for building energy consumption simulation[J]. J Xi'an Univ of Arch & Tech (Natural Science Edition), 47(2): 267–271.
|
|
李昀英, 宇如聪, 徐幼平, 等. 2003. 中国南方地区层状云的形成和日变化特征分析[J]. 气象学报, 61(6): 733–743.
DOI:10.11676/qxxb2003.074 Li Y Y, Yu R C, Xu Y P, et al. 2003. The formation and diurnal changes of stratiform clouds in southern China[J]. Acta Meteor Sinica, 61(6): 733–743.
DOI:10.11676/qxxb2003.074 |
|
刘可群, 陈正洪, 夏智宏. 2007. 湖北省太阳能资源时空分布特征及区划研究[J]. 华中农业大学学报, 26(6): 888–893.
Liu K Q, Chen Z H, Xia Z H. 2007. The characteristic analysis and division research of solar energy resource in Hubei province[J]. Journal of Huazhong Agricultural University, 26(6): 888–893.
|
|
申彦波, 常蕊, 杜江, 等. 2015. 吐鲁番地区可利用太阳能资源分析[J]. 高原气象, 36(9): 111–115.
Shen Y B, Chang R, Du J, et al. 2015. Analysis of the available solar energy resources in Turpan[J]. Plateau Meteor, 36(9): 111–115.
|
|
申彦波, 王香云, 王婷, 等. 2016. 中国典型地区水平总辐射辐照度频次特征[J]. 风能(8): 70–76.
Shen Y B, Wang X Y, Wang T, et al. 2016. Frequency characteristics of the global horizontal irradiation in typical cities over China[J]. Wind Energy(8): 70–76.
|
|
申彦波. 2010. 近20年卫星遥感资料在我国太阳能资源评估中的应用综述[J]. 气象, 36(9): 111–115.
DOI:10.7519/j.issn.1000-0526.2010.09.018 Shen Y B. 2010. Review of applications of satellite remote sensing data to solar energy resources assessment in China in recent 20 years[J]. Meteor Mon, 36(9): 111–115.
DOI:10.7519/j.issn.1000-0526.2010.09.018 |
|
王炳忠, 张富国, 李立贤. 1980. 我国的太阳能资源及其计算[J]. 太阳能学报, 1(1): 1–9.
Wang B Z, Zhang F G, Li L X. 1980. Solar energy resources in China[J]. Acta Energy Solaris Sinica, 1(1): 1–9.
|
|
辛渝, 赵逸舟, 毛炜峄, 等. 2011. 新疆太阳总辐射资料的均一性检验与气候学估算式的再探讨[J]. 高原气象, 30(4): 878–889.
Xin Y, Zhao Y Z, Mao W Y, et al. 2011. Homogeneity test of the total solar radiation data series and further research on climatological calculation over Xinjiang[J]. Plateau Meteor, 30(4): 878–889.
|
|
杨柳, 李昌华, 刘加平. 2006. 典型气象年生成方法及原始气象数据质量分析[J]. 气象科技, 34(5): 596–599.
Yang L, Li C H, Liu J P. 2006. Generating method of typical meteorological years and quality analysis of raw meteorological data[J]. Meteor Sci Technol, 34(5): 596–599.
|
|
郑有飞, 尹炤寅, 吴荣军, 等. 2012. 1960-2005年京津冀地区地表太阳辐射变化及成因分析[J]. 高原气象, 31(2): 436–445.
Zheng Y F, Yin S Y, Wu R J, et al. 2012. Analyses on variation and cause of surface solar radiation in Beijing, Tianjin and Hebei region from 1960 to 2005[J]. Plateau Meteor, 31(2): 436–445.
|
|
周扬, 吴文祥, 胡莹, 等. 2010. 西北地区太阳能资源空间分布特征及资源潜力评估[J]. 自然资源学报. 2010, 25(10): 1739–1749.
Zhou Y, Wu W X, Hu Y, et al. 2010. The temporal-spatial distribution and evaluation of potential solar energy resources in northwest China[J]. Journal of Natural Resources, 25(10): 1739–1749.
|
|
朱飙, 李春华, 方锋. 2010. 甘肃省太阳能资源评估[J]. 干旱气象, 28(2): 218–221.
Zhu B, Li C H, Fang F. 2010. Solar energy resource assessment in Gansu province[J]. J Arid Meteor, 28(2): 218–221.
|
2. Public Meteorological Service Center of China Meteorological Administration, Beijing 100081, China;
3. Wind and Solar Energy Resources Center of China Meteorological Administration, Beijing 100081, China
 2017, Vol. 36
2017, Vol. 36