2. 中国科学院大学, 北京 100049;
3. 中国科学院青藏高原地球科学卓越创新中心, 北京 100101
青藏高原(下称高原)平均海拔4 000 m以上, 有“世界屋脊”之称, 其高大的地形对大气环流造成的热力、动力作用不可忽视。那曲位于高原腹地, 是高原热力作用的核心区域。该地区下垫面为藏北高寒草甸的代表且藏北地面热源变化强度与高原东半部相反(季国良等, 2001); 土壤存在季节性冻融, 冻融过程使地气间能量交换加强(李述训等, 2002); 夏季那曲受高原季风影响, 降雨量充沛, 为高原季风气候区的代表。
地表感热通量和潜热通量是表征下垫面与大气之间相互作用的重要参数, 同时也是能量水分循环观测试验的重要内容, 为深入理解高原地气相互作用提供了可能。因此, 如何准确描述和计算湍流通量一直受到气象学者们的广泛关注。目前, 关于地表感热通量、潜热通量的计算方法主要分为两种, 一是直接计算方法, 即涡动相关法; 二是间接计算方法, 主要有空气动力学法、波文比法、地表能量平衡和空气动力学组合法(简称组合法)以及总体输送法等。高原上恶劣的自然条件, 交通不便, 气象观测台站稀少, 观测仪器参差不齐, 近地层梯度观测资料相对容易获得, 因此间接通量计算方法仍被广泛使用。空气动力学法依赖于半经验公式——莫宁-奥布霍夫(Monin-Obukhov)相似函数, 且在地表湍流通量计算过程中具有较好的稳定性。因为相似函数的参数化方案较多, 使湍流通量的计算结果存在差异(Dyer et al, 1974; Yaglom, 1977)。波文比法(Sun et al, 2003)计算的湍流通量满足能量平衡条件, 计算方法简单实用。但该方法在波文比为-1的情况下, 计算的感热通量、潜热通量不稳定。在Thom et al(1975)提出使用相似关系和能量平衡条件联合求解湍流通量后, 胡隐樵等(1991)结合波文比法和空气动力学法提出了组合法。该方法避免了对相似函数具体形式的依赖性, 同时满足能量平衡条件, 但组合法和波文比法存在相同的计算不稳定问题。总体输送法在确定总体输送系数的基础上, 利用温度和湿度梯度观测资料计算地表湍流通量。该方法原理简单, 计算方便, 适用于业务气象站和普通野外台站只有常规观测项目的情况。由于总体输送系数的参数化方案较多(Chen et al, 1985; 陈万隆等, 1984; 李国平等, 2002), 湍流通量结果差异较大。涡动相关法利用超声风、温仪和气体分析仪观测的高频三维风速以及空气温度和水汽脉动资料, 通过协相关分析直接计算湍流通量, 是目前认为最接近湍流实际情况的计算方法。但其依然存在一些缺陷, 如该仪器价格昂贵, 操作复杂; 其观测准确度受到仪器架设高度和风速等客观因素的影响(陈家宜等, 2006)。
关于高原近地层湍流通量的研究, 许多学者采用不同的通量计算方法做了大量的工作(李国平等, 2003; 阳坤等, 2010; 孙根厚等, 2016; 万云霞等, 2017)。但是单站多种通量计算方法的对比分析尚不多见, 特别是间接通量计算方法与涡动相关法的对比分析。为了检验各种间接通量计算方法在高寒草甸下垫面的适用性、稳定性以及差异性, 选取中国科学院那曲高寒气候环境观测研究站自动气象站(AWS)和涡动相关系统(EC)同期的常规、梯度和涡动观测资料, 基于空气动力学法、组合法、总体输送法以及涡动相关法计算高寒草地下垫面的湍流通量, 并对不同方法间计算结果的一致性和差异性进行分析, 为下一步基于长时间梯度观测资料选择合适的通量计算方法建立长时间连续高质量序列, 分析地面热源的长时间变化规律奠定基础。
2 资料概况和计算方法 2.1 资料概况利用中国科学院那曲高寒气候环境观测研究站BJ观测点(简称那曲站)2013年9月至2014年8月具有季节性代表的20天观测资料(秋季: 2013年11月7—11日; 冬季: 2014年1月6—10日; 春季: 2014年4月6—10日; 夏季: 2014年6月8—12日), 时间为北京时。BJ观测点是那曲站的主观测点, 位于西藏自治区那曲县罗玛镇娘曲村附近, 地理位置和海拔分别是31.37°N、91.90°E和4 509 m。那曲属于高原亚寒带季风半湿润气候区, 气候寒冷且相对干燥, 植被主要为高寒草甸或草原, 多年平均温度为-0.5 ℃, 平均年降水量为455.1 mm。那曲站BJ观测点四面开阔, 植被高度为10~20 cm。选用的观测资料包括:风速、气温、相对湿度、太阳总辐射、反射辐射、地面长波辐射、天空长波辐射、土壤温度、土壤含水量和土壤热通量, 以及涡动观测资料, 时间步长统一调整为30 min。具体观测仪器和架设高度(埋深)见表 1。
| 表 1 BJ站观测仪器说明 Table 1 Specification of observational instrument at BJ site |
由Monin-Obhukhov相似理论, 得到风速u, 位温θ, 湿度q的垂直廓线公式:
| $ u\left( z \right) - u\left( {{z_0}} \right) = \frac{{{u_ * }}}{k}\left[ {\ln \left( {\frac{z}{{{z_{0m}}}}} \right) - {\psi _m}\left( \zeta \right) + {\psi _m}\left( {{\zeta _{0m}}} \right)} \right], $ | (1) |
| $ \theta \left( z \right) - \theta \left( {{z_{0h}}} \right) = \frac{{{\theta _ * }}}{k}\left[ {\ln \left( {\frac{z}{{{z_{0h}}}}} \right) - {\psi _h}\left( \zeta \right) + {\psi _h}\left( {{\zeta _{0h}}} \right)} \right], $ | (2) |
| $ q\left( z \right) - q\left( {{z_{0q}}} \right) = \frac{{{q_ * }}}{k}\left[ {\ln \left( {\frac{z}{{{z_{0q}}}}} \right) - {\psi _q}\left( \zeta \right) + {\psi _q}\left( {{\zeta _{0q}}} \right)} \right], $ | (3) |
式中: u、θ、q、u*、θ*、q*、k分别是风速(单位: m·s-1)、位温(单位: K)、比湿(单位: kg·kg-1)、摩擦速度(单位: m·s-1)、位温尺度(单位: K)、比湿尺度(单位: kg·kg-1)以及Karman常数(取0.4); ψm(ζ)、ψh(ζ)和ψq(ζ)分别为动量、热量和水汽积分形式的相似函数, 采用Busurger-Dyer形式(Businger et al, 1971; Yaglom, 1977)。
在不稳定条件下, 即ζ≤0时,
| $ {\psi _m}\left( \zeta \right) = \ln \left[ {\left( {\frac{{1 + {x^2}}}{2}} \right){{\left( {\frac{{1 + x}}{2}} \right)}^2}} \right] - 2{\tan ^{ - 1}}x + \frac{{\rm{ \mathsf{ π} }}}{2}, $ | (4) |
| $ {\psi _h}\left( \zeta \right) = 2\ln \left( {\frac{{1 + y}}{2}} \right), $ | (5) |
式(4)、(5)中:
在稳定条件下, 即ζ>0时,
| $ {\psi _m}\left( \zeta \right) = - 6\zeta , $ | (6) |
| $ {\psi _h}\left( \zeta \right) = - 7.8\zeta , $ | (7) |
式中:
| $ L = - \frac{{u_ * ^3}}{{k\frac{g}{{\bar \theta }}\overline {w'\theta '} }} = \frac{{u_ * ^2}}{{k\frac{g}{{\bar \theta }}{\theta _ * }}}, $ | (8) |
当满足以下条件时, L收敛
| $ \left| {\frac{{L\left( n \right) - L\left( {n - 1} \right)}}{{L\left( n \right)}}} \right| \le 0.001, $ | (9) |
求出u*, θ*, q*, 带入下式计算感热、潜热通量
| $ H = - \rho {c_p}{u_ * }{\theta _ * }, $ | (10) |
| $ LE = - \rho \lambda {u_ * }{q_ * }, $ | (11) |
式中: ρ为空气密度(单位: kg·m-3); cp为空气定压比热[单位: J·(K·kg)-1]; λ为水的汽化潜热(单位: J·kg-1)。
2.2.2 组合法(Combination Method, CM)利用能量平衡方程H+LE=Rn-G0以及廓线公式(1)、(2)、(3)的微分形式计算出感热、潜热通量:
| $ H = - \rho {c_p}{k^2}{z^2}\frac{{\partial u}}{{\partial z}}\frac{{\partial \theta }}{{\partial z}}F = {H_0}F, $ | (12) |
| $ LE = - \rho \lambda {k^2}{z^2}\frac{{\partial u}}{{\partial z}}\frac{{\partial q}}{{\partial z}}F = \left( {L{E_0}} \right)F, $ | (13) |
| $ F = \frac{{{R_n} - {G_0}}}{{{H_0} + L{E_0}}}, $ | (14) |
式中: Rn是净辐射通量(单位: W·m-2); G0代表地表土壤热通量(单位: W·m-2)。
2.2.3 总体输送法(Mass Transfer Method, TM)通过垂直廓线公式(李国平等, 2002)得到2013年9月至2014年8月的总体输送系数, 取平均值为0.005 4, 计算地表感热、潜热通量:
| $ H = \rho {c_p}{c_H}U\left( {{T_s} - T} \right), $ | (15) |
| $ LE = \rho \lambda {c_\lambda }U\left( {{q_s} - q} \right), $ | (16) |
假设cH=cλ, cH表示热量的总体输送系数。T, q分别为1.03 m高度的气温(单位: K)和比湿(单位: kg·kg-1); Ts, qs分别为地表温度(单位: K)和地表比湿(单位: kg·kg-1), qs通过地表温度计算得到; U为10.36 m高度的风速(单位: m·s-1)。
2.2.4 涡动相关法(Eddy Covariance, EC)涡动相关法是目前测量地气间湍流通量最好, 最直接的方法, 主要是利用超声风温仪和气体分析仪测量高频瞬时风、温、湿脉动, 并通过协方差分析计算得到。计算公式如下:
| $ H = \rho {c_p}\overline {\theta 'w'} , $ | (17) |
| $ LE = \rho \lambda \overline {q'w'} , $ | (18) |
式中: θ′、w′、q′分别为温度、风速、湿度的脉动值。
2.3 地表净辐射和土壤热通量的计算地表净辐射Rn由观测辐射四分量计算得到:
| $ {R_n} = \left( {{R_s} \downarrow - {R_s} \uparrow } \right) + \left( {{R_l} \downarrow - {R_l} \uparrow } \right), $ | (19) |
式中: Rs↓和Rs↑分别为太阳总辐射(单位: W·m-2)和反射辐射(单位: W·m-2); Rl↓和Rl↑分别为天空长波辐射(单位: W·m-2)和地面长波辐射(单位: W·m-2)。
地表土壤热流量G0计算公式(Gentine et al, 2012)如下:
| $ {G_0}\left( t \right) = {G_z}\left( t \right) + {c_v}\frac{{\partial {T_s}}}{{\partial t}}\Delta z, $ | (20) |
式中: Gz(t)是t时刻10 cm深度土壤热通量(单位: W·m-2); Ts为土壤深度4 cm处的土壤温度(单位: K); Δz为热通量板到地表的深度; cv为土壤热容量(单位: J·m-3·k-1)(Tanaka et al, 2001)。
3 数据处理和质量控制 3.1 涡动数据处理利用超声仪观测的高频风、脉动温度资料, 通过涡动相关法计算感热通量、潜热通量, 以向上为正。采用的是美国LI-COR公司推出的EddyPro软件。该软件在计算感热通量和潜热通量时, 并对数据进行了严格的质量控制: (1)剔除环境因子对传感器的干扰或者电路不稳定带来的野点; (2)利用坐标旋转对坐标平面倾斜修正; (3)对频率响应的校正; (4)超声虚温校正; (5)Webb-Pearman-Leuning密度校正。同时EddyPro软件还可以根据平稳性假设检验和湍流整体特征检验对通量结果做质量评估, 评估标准如表 2所示。为了保障涡动数据的准确度, 只采用总体质量数为0和1的湍流通量数据比较分析。
| 表 2 地表湍流通量质量评估标准 Table 2 Evaluation criteria of surface flux quality |
自动气象站观测数据受观测仪器、观测技术、测站位置、观测方法的影响, 使观测资料质量大打折扣。因此气象观测资料可能产生随机误差、系统性误差、偶然误差。为了避免由于低质量观测数据带来的计算误差, 将先对观测数据进行质量控制, 主要包括:逻辑极值检验、僵值检验、时间一致性检查以及相似一致性检查四种检查(王超等, 2010)。图 1为典型不符合逻辑值检验的风速数据, 图 2为未通过一致性检验的温度数据。一致性检验结合大气边界层塔梯度资料进行分析。由于观测仪器不同导致观测数值大小存在差异, 但变化趋势基本一致。质量控制后, 空值采用线性插补的方法填补, 方法如下:
| $ {D_k} = {D_{k - 1}} + \frac{{{D_{k - 1}} - {D_i}}}{{k - i - 1}}, $ | (21) |

|
图 1 质量控制前(a)后(b), 典型未通过极值检验的2014年1月1日的风速数据 Figure 1 Typical extreme errors of wind speed data on 1 January 2014 before (a) and after (b) quality control |
|
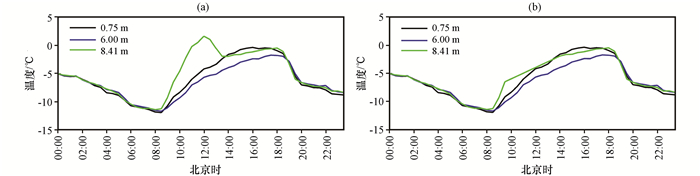
图 2 质量控制前(a)后(b), 典型未通过一致性检验的2013年11月11日的温度数据 Figure 2 Typical consistency errors of temperature data on 11 November 2013 before (a) and after (b) quality control |
式中: Dk、Dk-1、Di分别为缺测值、缺测前一时刻值、缺测值后首个非缺测值; i, k代表不同时刻。插补后气象观测数据完整, 数据质量得到保障。
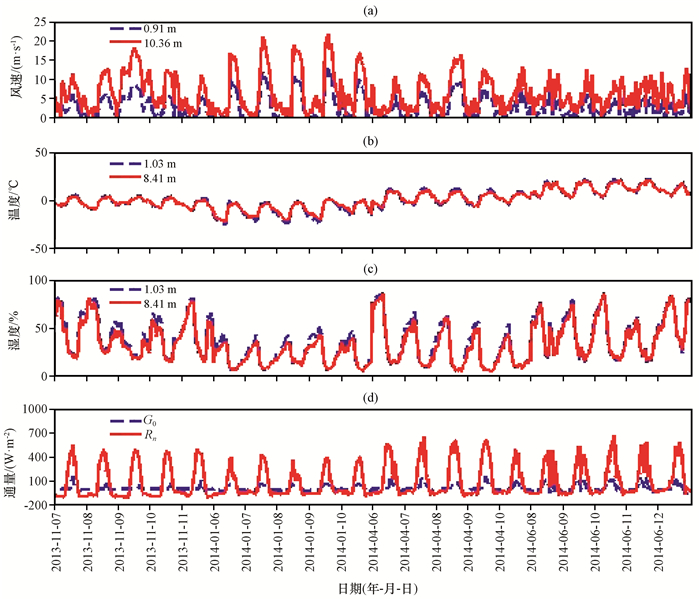
通过BJ站大气边界层塔质量控制后的风速、温度、湿度、地表土壤热通量和净辐射通量的时间序列(图 3)可以看出, 高层风速始终大于低层风速[图 3(a)], 梯度明显, 动量向下输送。以2014年1月和4月为代表的冬、春季风速较大, 7月为代表的夏季风速最小。不同高度温度整体变化趋势基本一致[图 3(b)], 满足季节变化规律, 冬季温度日变化振幅强, 夏季较弱。两层高度的温度差不明显。不同高度相对湿度也具有相同的变化特征[图 3(c)], 寒冷干燥的冬季湿度较小, 两层比湿变化曲线几乎重合。高原季风盛行期相对湿度突变, 明显增大。地表土壤热流量和净辐射通量日变化特征明显[图 3(d)], 冬季日变化曲线光滑, 晴天居多; 夏季多雨, 净辐射曲线多呈锯齿状。
|
图 3 BJ自动气象站质量控制后的风速(a)、温度(b)、相对湿度(c)、地表土壤热通量和净辐射通量(d)的时间序列 Figure 3 Time series of wind speed (a), air temperature (b), specific humidity (c), surface heat flux and net radiation(d) of automatic weather station after quality control |
综合以上分析可知, 常规气象数据在观测期间完整性较好, 数据质量较高, 较为典型的代表了藏北高寒草地的下垫面特征, 同时也为空气动力学法、组合法以及总体输送法计算感热通量、潜热通量提供了数据保障。
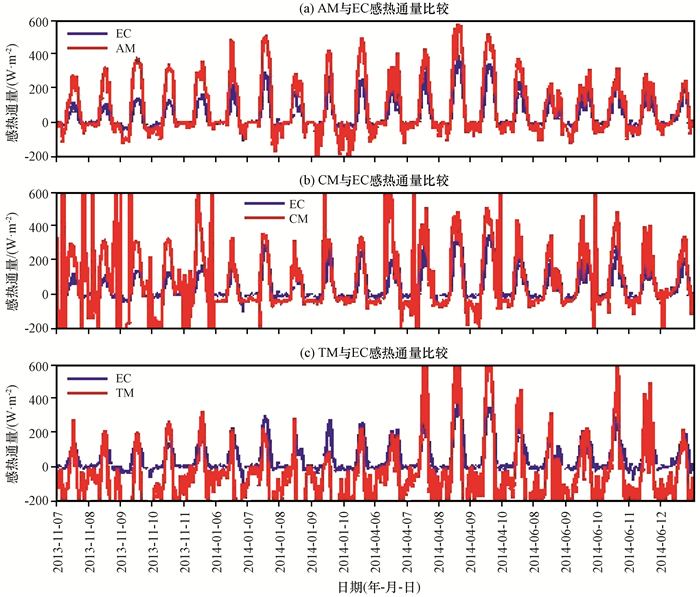
4 结果分析 4.1 四种方法计算的湍流通量日变化特征从AM和EC计算的感热通量和潜热通量的日变化[图 4(a), 图 5(a)]可以看出, 2013年11月7—11日为秋季代表的EC计算的感热通量日变化最大值范围为115~170 W·m-2, 潜热通量日变化最大值范围为130~180 W·m-2; 2014年1月6 —10日为冬季代表的涡动相关法计算的感热通量日变化最大值范围为190~300 W·m-2, 潜热通量日变化最大值范围为20~32 W·m-2; 2014年4月6—10日为春季代表的EC计算的感热通量日变化最大值范围为210~400 W·m-2, 潜热通量日变化最大值范围为40~105 W·m-2; 2014年6月8—12日为夏季代表的EC计算的感热通量日变化最大值范围为200~300 W·m-2, 潜热通量日变化最大值范围为140~290 W·m-2。整个时间序列, AM计算的感热通量最大值均大于EC感热通量日变化最大值。而潜热通量最大值小于涡动结果。AM在夜晚计算的感热通量和潜热通量振幅较小, 与涡动湍流通量较为吻合。
|
图 4 四种方法计算的高寒草地感热通量(a~c)的时间序列 Figure 4 Time series of sensible heat flux (a~c) computed by four methods |
|
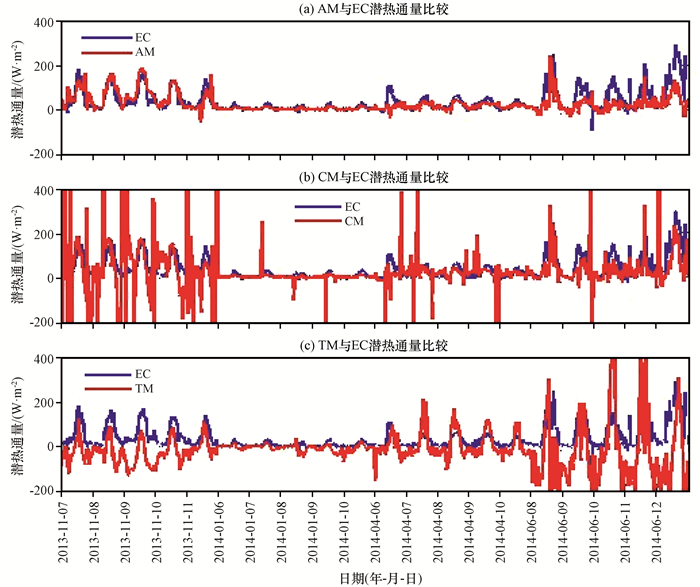
图 5 四种方法计算的高寒草地潜热通量(a~c)的时间序列 Figure 5 Time series of latent heat flux (a~c) computed by four methods |
CM和EC计算的感热和潜热通量的变化[图 4(b), 图 5(b)]可以看出, 整个观测期, 白天CM计算的感热通量最大值较EC感热通量日变化最大值偏大, 潜热通量值偏小。夜晚以及凌晨CM计算的感热通量和潜热通量数值存在一定的发散现象, 曲线变化出现震荡和尖峰组成。因此夜晚CM计算结果不可靠, 主要是由于CM中未订正的感热通量和潜热通量之和接近零造成的, 这与杨娟等(2006)利用波文比法研究地表通量时, 波文比接近-1造成的发散现象相似。
TM和EC计算的感热和潜热通量的变化[图 4(c), 图 5(c)]可以看出, 观测期间TM计算的感热、潜热通量较EC湍流通量在白天变化趋势基本一致; 在夜晚TM计算的湍流通量存在明显的波动不稳定。
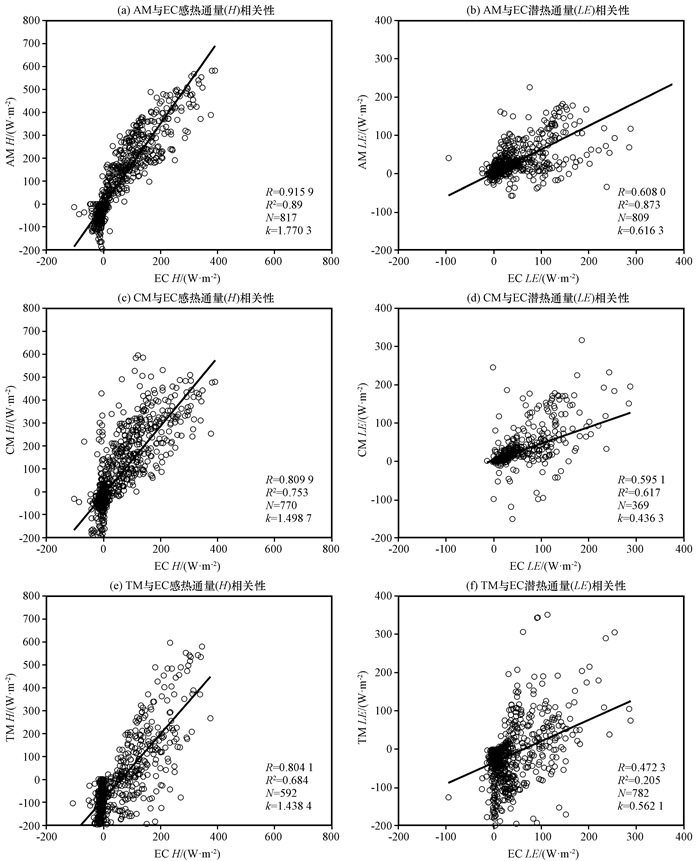
4.2 四种通量计算方法的相关性分析为了进一步对比四种方法计算的湍流通量, 分别对空气动力学法(AM), 组合法(CM), 总体输送法(TM)与涡动相关法(EC)的湍流通量进行相关性分析(图 6)。图 6中的黑色实线是回归直线, R为相关系数, R2为决定系数, N为样本数据容量, K为拟合直线斜率, 以上数值均在图中标出。
|
图 6 不同方法计算的高寒草地感热(左)、潜热(右)通量的相关性 Figure 6 The correlation of sensible heat (left) and latent heat (right) fluxes over alpine grassland computed by different methods |
从AM与EC计算的感热通量(H)和潜热通量(LE)的相关性比较[图 6(a)]可以看出, AM计算的感热、潜热通量和EC计算结果具有较好的相关性, 相关系数分别达到0.915 9和0.608 0。拟合回归直线的拟合程度较高, 但斜率与1偏差较大, 分别为1.770 3和0.616 3。刘鹏飞等(2010)在金塔绿洲比较变分法与AM计算的通量相关性时, 发现感热通量在小于零时, 数据存在拐点, 图 6(a)和6(b)中AM计算的感热通量数据与EC计算结果的相关性分析中未出现拐点, 与选择的相似函数的参数化方案有关。图 6(c)、(d)为CM和EC计算的感热通量和潜热通量的相关性比较。为了避免夜晚发散数据带来的影响, CM做相关性分析前已剔除极端数据。CM和EC计算的感热通量、潜热通量的相关性分别为0.809 9和0.595 1, 略低于AM相关性结果。拟合回归直线斜率分别为1.498 7和0.436 3。TM计算的湍流通量数据在夜晚波动较大, 为保障TM与EC湍流通量的相关性, 故剔除异常值。TM和EC计算的感热、潜热通量相关性[图 6(e), (f)]分析表明, TM与EC湍流通量的相关性分别为0.804 1和0.472 3, 拟合回归直线斜率分别为1.438 4和0.562 1。
4.3 不同方法的能量闭合状况能量平衡比率CR反应了能量平衡方程的闭合程度, 同时也是衡量不同方法计算得到的通量数据质量的标准之一(Culf et al, 2004; Zhang, 2005)。根据能量平衡方程, CR定义为:
| $ CR = \frac{{H + LE}}{{{R_n} - {G_0}}}, $ | (22) |
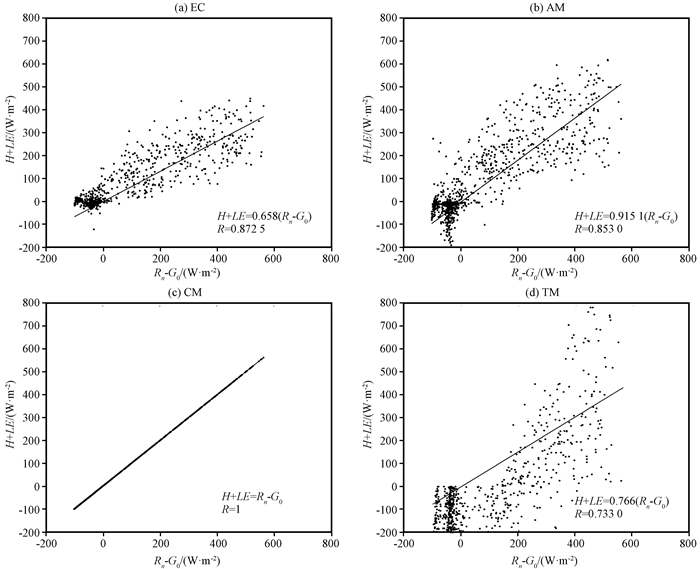
CR越接近1, 表示能量闭合程度越高。通过用不同方法计算的BJ站能量闭合状况(图 7)可以看出, 不同通量计算方法的原理各不相同, 故而能量平衡比率差异较大。CM根据能量平衡方程得到, 故其能量平衡比率恒等于1[图 7(c)]。EC、AM以及TM得到的CR分别为0.658, 0.915 1和0.766。AM、TM得到的能量闭合率高于EC的闭合率, 因为通过两种方法计算的感热通量数据大于EC得到的感热通量。EC、AM以及TM的湍流通量和与可利用能量的相关系数分别为0.872 5, 0.853 0和0.733 0。EC得到的相关系数高于AM和TM的相关系数。EC计算的BJ站CR为0.658, 与葛骏等(2016)在藏北北麓河站得到的CR值0.65相同。藏高原积雪覆盖时, 雪盖融化或升华吸收的能量导致CR偏低(Yao et al, 2008)。
|
图 7 四种方法(a~d)计算的高寒草地能量闭合状况 Figure 7 Surface energy closure over alpine grassland computed by four methods (a~d) |
从AM、CM和TM与EC的通量误差(表 3)可知, AM、CM以及TM与EC计算的感热通量的平均偏差分别为40.274, 30.592和-65.865;相对标准差分别为0.933, 1.016和1.095。AM、CM以及TM与EC计算的潜热通量的平均偏差分别为-9.866, -11.756和-49.758;相对标准差分别为0.733, 1.055和1.405。从表 3中可以看出, CM感热通量平均偏差最小, AM潜热通量的平均偏差的绝对值最小; 感热潜热通量的相对标准差最小的是AM, 其次是CM, 最后为TM。
| 表 3 空气动力学法(AM)、组合法(CM)和整体输送法(TM)与涡动相关法(EC)的通量误差 Table 3 The flux error of aerodynamic method, combination method, transfer method and eddy correlation method |
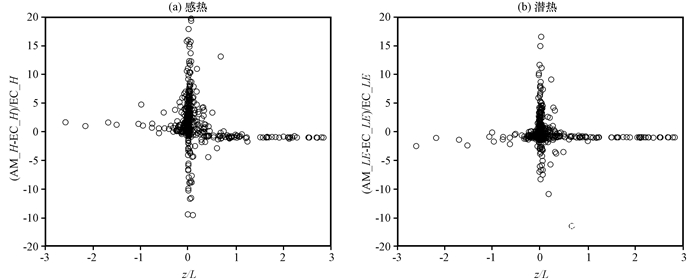
依靠半经验相似理论的AM的相似函数是表征大气稳定度参数的函数。基于数值迭代方法求解的AM和EC计算的湍流通量差异应该和大气稳定度参数相关。从AM和EC计算的感热通量的相对偏差[(AM_H-EC_H)/ EC_H]、潜热通量的相对偏差[(AM_LE-EC_LE)/ EC_LE]和大气稳定度参数z/L的关系(图 8)可以看出, AM和EC计算得到的感热和潜热通量的相对偏差与大气稳定度具有良好的关系, 说明大气稳定度参数z/L接近零是该方法误差的主要来源。
|
图 8 空气动力学法与涡动相关法感热(a)、潜热(b)通量的相对偏差与大气稳定度z/L的关系 Figure 8 Correlations between the ratio of the difference of the sensible heat (a) and latent heat (b) fluxes from the aerodynamic method and the eddy covariance to the eddy flux and the atmospheric stability (z/L) |
从组合法的计算式(12)、(13)、(14)可知, 当H0+λLE0接近零时, 组合法计算结果出现发散。
对式(12)、(13)关于H0+λLE0微分:
| $ \begin{array}{*{20}{c}} {{\sigma _H} = \frac{{{H_0}}}{{{H_0} + \lambda L{E_0}}} \cdot {\sigma _{\left( {{R_n} - {G_0}} \right)}} + \frac{{\left( {{R_n} - {G_0}} \right)}}{{{H_0} + \lambda L{E_0}}} \cdot {\sigma _{\left( {{H_0}} \right)}}}\\ { - \frac{{\left( {{R_n} - {G_0}} \right) \cdot {H_0}}}{{{{\left( {{H_0} + \lambda L{E_0}} \right)}^{ - 2}}}} \cdot {\sigma _{\left( {{H_0} + \lambda L{E_0}} \right)}},} \end{array} $ | (23) |
| $ \begin{array}{*{20}{c}} {{\sigma _{LE}} = \frac{{L{E_0}}}{{{H_0} + \lambda L{E_0}}} \cdot {\sigma _{\left( {{R_n} - {G_0}} \right)}} + \frac{{\left( {{R_n} - {G_0}} \right)}}{{{H_0} + \lambda L{E_0}}} \cdot {\sigma _{\left( {L{E_0}} \right)}}}\\ { - \frac{{\left( {{R_n} - {G_0}} \right) \cdot L{E_0}}}{{{{\left( {{H_0} + \lambda L{E_0}} \right)}^{ - 2}}}} \cdot {\sigma _{\left( {{H_0} + \lambda L{E_0}} \right)}},} \end{array} $ | (24) |
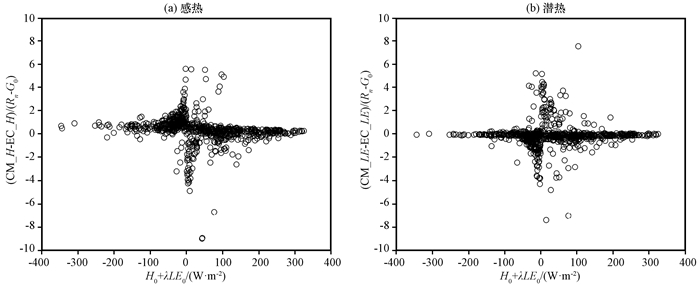
式中: σ表示物理量关于H0+λLE0的微分形式。当H0+λLE0接近零时, 公式右边第1项、第2项相对于第3项为小项, 则组合法感热、潜热通量的误差主要由第3项贡献。当H0+λLE0接近零时, (H0+λLE0)-2迅速增大。通过图 9可知, 组合法与涡动相关法的通量偏差与可用能量比值和H0+λLE0具有较好的关系, 变化趋势与
|
图 9 组合法与涡动相关法感热(a)、潜热(b)通量偏差和可利用能量(Rn-G0)比值与H0+λLE0的关系 Figure 9 Correlations between the ratio of the difference of the sensible heat (a) and latent heat (b) fluxes from the combination method and the eddy covariance to the total available energy flux (Rn-G0) and H0+λLE0 |
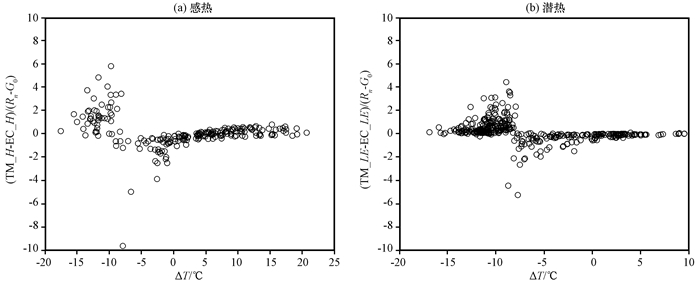
基于廓线法(李国平等, 2002)计算总体输送系数的参数化方案中假设地面粗糙度不变。杨耀先等(2014)利用涡动观测数据发现地表粗糙度具有明显的季节变化。同时, 总体输送系数值与观测梯度高度地选取也有关。总体输送系数确定后, 总体输送法计算的湍流通量的数值决定于地表温度与气温的差值ΔT。由总体输送法与涡动相关法通量偏差和可利用能量比值与地气温差ΔT的关系(图 10)可知, 随着ΔT逐渐减小, 总体输送法计算的湍流通量数值波动明显。ΔT<0 ℃时, 总体输送法较涡动相关法计算的感热通量偏差开始增大; ΔT<-5 ℃时, 总体输送法计算的潜热通量偏差开始增大。
|
图 10 总体输送法与涡动相关法感热(a)、潜热(b)通量偏差和可利用能量比值(Rn-G0)与地气温差(ΔT)的关系 Figure 10 Correlations between the ratio of the difference of the sensible heat (a) and latent heat (b) fluxes from the mass transfer method and the eddy covariance to the total available energy flux (Rn-G0) and the difference between soil temperature and air temperature (ΔT) |
利用那曲站自动气象站(AWS)和涡动相关系统(EC)观测资料, 基于四种间接和直接通量计算方法计算了高寒草地下垫面的湍流通量, 并对不同方法计算结果间的一致性和差异性进行了分析, 得出以下结论:
(1) 空气动力学法、组合法和总体输送法计算的感热通量日变化振幅较涡动相关法偏大; 潜热通量日变化振幅偏小。
(2) 空气动力学法、组合法、总体输送法分别与涡动相关法的感热通量具有较好的相关性, 均在0.8以上; 空气动力学法和组合法的潜热通量相关性均在0.6左右, 总体输送法的相关性较低为0.472。
(3) 涡动相关法得到的能量闭合率0.658;总体输送法能量闭合率为0.766;空气动力学法闭合率最高为0.915。而涡动相关法得到的湍流通量和与可利用能量的相关性最高, 为0.872 5。
(4) 组合法和空气动力学法计算的湍流通量平均偏差均较小, 总体输送法较大。空气动力学法与涡动相关法的通量的差异和大气稳定度相关, 在大气稳定度参数z/L接近零是该方法误差的主要来源; 当H0+λLE0接近零时, 组合法计算湍流通量数据与涡动相关法的湍流通量差异较大; 总体输送法通量的偏差数值较前两种方法大, 主要集中在地表温度与气温的差值ΔT小于零时。
由于藏北高原上涡动仪器普及较晚, 观测时间短, 对地表湍流通量的长时间特征研究相对薄弱。而大气边界层塔、自动气象站观测时间长, 律定间接通量计算方法, 结合多年梯度观测数据, 建立地表湍流通量的长时间高质量连续序列, 分析藏北高原地面热源强度及其组分配置的长时间变化规律将是下一步的工作重点。
Businger J A, Wyngaard J C, Izumi Y, et al. 1971. Flux-profile relationships in the atmospheric surface layer[J]. J Atmos Sci, 28(28): 181–189.
|
|
Culf A D, Foken T, Gash J H C. 2004. The energy balance closure problem[M]. Vegetation, Water, Humans and the Climate: Springer Berlin Heidelberg, 159-166.
|
|
Chen L, Reiter E R, Feng Z. 1985. The atmospheric heat source over the Tibetan Plateau:May-August 1979[J]. Mon Wea Rev, 113(10): 1771–1790.
DOI:10.1175/1520-0493(1985)113<1771:TAHSOT>2.0.CO;2 |
|
Dyer A J. 1974. A review of flux-profile relationships[J]. Bound-Layer Meteor, 7(3): 363–372.
DOI:10.1007/BF00240838 |
|
Gentine P, Entekhabi D, Heusinkveld B. 2012. Systematic errors in ground heat flux estimation and their correction[J]. Water Resour Res, 48(9): 9541.
DOI:10.1029/2010WR010203 |
|
Sun R, Liu C. 2003. A review on research of land surface water and heat fluxes[J]. Chinese J Appl Ecology, 14(3): 434–438.
|
|
Thom A S, Stewart J B, Oliver H R, et al. 1975. Comparison of aerodynamic and energy budget estimates of fluxes over a pine forest[J]. Quart J Roy Meteor Soc, 101(427): 93–105.
DOI:10.1002/(ISSN)1477-870X |
|
Tanaka K, Ishikawa H, Hayashi T, et al. 2001. Surface energy budget at Amdo on the Tibet Plateau using GAME/Tibet IOP98 data[J]. J Meteor Soc Japan, 79(1B): 505–517.
DOI:10.2151/jmsj.79.505 |
|
Yaglom A M. 1977. Comments on wind and temperature flux-profile relationships[J]. Bound-Layer Meteor, 11(1): 89–102.
DOI:10.1007/BF00221826 |
|
Yao J M, Zhao L, Ding Y J, et al. 2008. The surface energy budget and evapotranspiration in the Tanggula region on the Tibetan Plateau[J]. Cold Regions Sci Technol, 52(3): 326–340.
DOI:10.1016/j.coldregions.2007.04.001 |
|
陈家宜, 范邵华, 赵传峰, 等. 2006. 涡旋相关法测定湍流通量偏低的研究[J]. 大气科学, 30(3): 423–432.
Chen J Y, Fan S H, Zhao C F, et al. 2006. The underestimation of the turbulent fluxes in Eddy Correlation techniques[J]. Chinese J Atmos Sci, 30(3): 423–432.
|
|
陈万隆, 翁笃鸣, 1984. 关于青藏高原感热和潜热旬总量计算方法的初步研究[C]//青藏高原气象科学实验论文集(二). 北京: 科学出版社, 35-45.
Chen W L, Weng D M, 1984. Preliminary study on calculation method of sensible heat and latent heat in Tibetan Plateau[C]//Experimental papers on Meteorological Sciences of the Qinghai Tibet Plateau (2). Beijing: Science Press, 35-45.
|
|
葛骏, 余晔, 李振朝, 等. 2016. 青藏高原多年冻土区土壤冻融过程对地表能量通量的影响研究[J]. 高原气象, 35(3): 08–620.
Ge J, Yu Y, Li Z C, et al. 2016. Impacts of freeze/thaw processes on land durface rnergy gluxes in the permafrost region of Qinghai-Xizang Plateau[J]. Plateau Meteor, 35(3): 08–620.
DOI:10.7522/j.issn.1000-0534.2016.00032 |
|
胡隐樵, 奇跃进. 1991. 组合法确定近地面层湍流通量和通用函数[J]. 气象学报, 49(1): 46–53.
Hu Y, Qi Y J. 1991. The combinatory method to determine the turbulent fluxes and the universal functions in the surface layer[J]. Acta Meteor Sinica, 49(1): 46–53.
|
|
季国良, 时兴和, 高务祥. 2001. 藏北高原地面加热场的变化及其对气候的影响[J]. 高原气象, 20(3): 239–244.
Ji G L, Shi X H, Gao W X. 2001. The variation of surface heating field over northern Qinghai-Tibet Plateau and its effect on climate[J]. Plateau Meteor, 20(3): 239–244.
|
|
李述训, 南卓铜, 赵林. 2002. 冻融作用对地气系统能量交换的影响分析[J]. 冰川冻土, 24(5): 506–511.
Li S X, Nan Z T, Zhao L. 2002. Impact of soil freezing and thawing process on thermal exchange between atmosphere and ground surface[J]. Journal Glaciology and Geocryology, 24(5): 506–511.
|
|
李国平, 赵邦杰. 2002. 青藏高原总体输送系数的特征[J]. 气象学报, 60(1): 60–67.
Li G P, Zhao B J. 2002. Characteristics of bulk transfer coefficients over the Tibetan plateau[J]. Acta Meteor Sinica, 60(1): 60–67.
|
|
李国平, 段廷扬, 吴贵芬. 2003. 青藏高原西部的地面热源强度及地面热量平衡[J]. 地理科学, 23(1): 13–18.
Li G P, Duan T Y, Wu G F. 2003. The intersity of surface heat source and surface heat balance on the western Qinghai-Xizang Plateau[J]. Science Geographica Sinica, 23(1): 13–18.
|
|
刘鹏飞, 刘树华, 胡非, 等. 2010. 湍流通量计算方法和误差的比较研究[J]. 气象学报, 68(4): 487–500.
Liu P F, Liu S H, Hu F, et al. 2010. A comparison of the different methods for estimating turbulent fluxes and their errors[J]. Acta meteor Sinica, 68(4): 487–500.
|
|
孙根厚, 胡泽勇, 王介民, 等. 2016. 那曲地区两种空间尺度感热通量的对比分析[J]. 高原气象, 35(2): 285–296.
Sun G H, Hu Z Y, Wang J M, et al. 2016. Comparison analysis of sensible heat fluxes at two spatial scales in Naqu area[J]. Plateau Meteor, 35(2): 285–296.
DOI:10.7522/j.issn.1000-0534.2015.00088 |
|
王超, 韦志刚, 李振朝. 2010. 敦煌戈壁气象塔站资料的质量控制[J]. 干旱气象, 28(2): 121–127.
Wang C, Wei Z G, Li Z C. 2010. A quality control routine for Dunhuang Gobi meteorology tower data[J]. J Arid Meteor, 28(2): 121–127.
|
|
万云霞, 张宇, 张瑾文, 等. 2017. 感热变化对东亚地区大气边界层高度的影响[J]. 高原气象, 36(1): 173–182.
Wan Y X, Zhang Y, Zhang J W, et al. 2017. Influence of sensible heat on planetary boundary layer height in East Asia[J]. Plateau Meteor, 36(1): 173–182.
DOI:10.7522/j.issn.1000-0534.2016.00001 |
|
阳坤, 郭晓峰, 武炳义. 2010. 青藏高原地表感热通量的近期变化趋势[J]. 中国科学:地球科学, 40(7): 923–932.
Yang K, Guo X F, Wu B Y. 2010. Recent trends in surface sensible heat flux on the Tibetan Plateau[J]. Sci China Earth Sci, 40(7): 923–932.
|
|
杨娟, 周广胜, 王云龙, 等. 2006. 基于变分方法的内蒙古典型草原水热通量估算[J]. 应用生态学报, 17(11): 2046–2051.
Yang J, Zhou G S, Wang Y L, et al. 2006. Estimation of sensible and latent heat fluxes of typical steppe in inner Mongolia based on variational method[J]. Chinese J Appl Ecology, 17(11): 2046–2051.
|
|
杨耀先, 李茂善, 胡泽勇, 等. 2014. 藏北高原高寒草甸地表粗糙度对地气通量的影响[J]. 高原气象, 33(3): 626–636.
Yang Y X, Li M S, Hu Z Y, et al. 2014. Influence of surface roughness on surface-air fluxes in alpine meadow over the Norther Qinghai-Xizang Plateau[J]. Plateau Meteor, 33(3): 626–636.
DOI:10.7522/j.issn.1000-0534.2013.00199 |
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Center for Excellence in Tibetan Plateau Earth Science, Chinese Academy of Science, Beijing 100101, China
 2018, Vol. 37
2018, Vol. 37
