Lorenz (1963)研究热对流不稳定时提出大气是一个强迫耗散非线性系统, 大气存在着“混沌现象”, 其内部运动具有随机性, 导致确定性预报发展遇到瓶颈, 在此基础上催生了基于大气运动非线性和复杂性的多值概率论的预报形式——集合预报(杜钧, 2002), 并在最近几十年内得到迅速发展。现在世界上主要的数值预报中心均已建立了业务化集合预报系统。集合预报最初被应用于全球中长期数值预报, 逐渐发展到短期天气预报, 同时在空间尺度上则由全球范围向局地化预报发展, 在此期间形成一系列成熟有效的初值扰动生成方法。其中Toth et al(1993, 1997)提出的增长模繁殖法(Breeding of Growing Modes, BGM)以其计算成本相对较低的优势得到发展, 并应用到美国国家环境预报中心(National Centers for Environmental Prediction, NCEP)的集合预报业务系统中。随着资料同化技术的发展, Bishop et al(1999, 2001)提出了建立在BGM法基础上的集合变换法(Ensemble Transformation, ET)和集合变换卡尔曼滤波法(Ensemble Transform Kalman Filter, ETKF), 两者产生的快速增长扰动受到资料同化系统输入的分析误差协方差矩阵的控制, 得到分布在多个独立、正交、不相关方向上的扰动场。
随着对灾害性极端天气预报需求的不断提高, 对流尺度天气预报的重要性便日益凸显。但由于对流尺度天气系统时空尺度小的特点和其固有的高度非线性动力、物理过程, 对流尺度灾害性天气的精确预报仍面临着巨大的挑战。同时业务化数值天气预报分辨率不够高的问题也是导致预报不确定性的因素之一, 因此发展高分辨率的对流尺度集合预报显得尤为重要。近年来, 美国国家大气研究中心(National Center for Atmospheric Research, NCAR)和美国俄克拉荷马大学风暴分析与预测中心(Center for Analysis and Prediction of Storms, CAPS)以降水和极端天气的指示作用作为评估重点, 进行了一系列对流尺度集合预报试验。其中NCAR用内层3 km分辨率在全美区域(CONUS)通过连续循环集合卡尔曼滤波(Ensemble Kalman Filter, EnKF)对集合预报系统进行初始化, 开展了连续的对流尺度集合预报业务试验以及个例研究, 并对试验结果进行了初步的分析(Schwartz et al, 2014, 2015a, 2015b), 表明基于EnKF的对流尺度集合预报系统是可以实现业务化的。CAPS在每年春季集中开展了对流尺度集合预报试验, 通过初始场扰动、物理过程和模式生成4 km分辨率的集合成员构成集合预报系统, 并对预报结果进行了与物理过程和后处理过程有关的敏感性研究和检验(Xue et al, 2007, 2010; Kong et al, 2008, 2009; Clark et al, 2012), 结果表明对流尺度集合预报能够提高一定区域范围的降水强度识别能力, 对高影响对流天气事件的预报有指导意义。
近年来, 国内学者主要对局地中尺度集合预报进行了研究。王晨稀等(2006, 2008)建立了上海区域集合预报系统并对一次局地短时强降水过程进行了集合预报研究, 结果表明, 在此过程中考虑模式物理过程、初值和侧边界不确定性的集合预报效果总体好于没有考虑侧边界不确定性的集合预报效果。高峰等(2010)针对美国俄州典型超级单体风暴通过Monte-Carlo和BGM两种方法构造风暴尺度集合预报试验, 检验了BGM法应用于风暴尺度集合预报的合理性和价值。庄潇然等(2016)考虑不同尺度特征的初始扰动与侧边界扰动相互作用构造对流尺度集合预报, 结果对构建不同类型强对流天气的初始扰动、侧边界扰动方案提供了合理的依据, 并利用混合初值扰动法对北京“7·21”暴雨进行风暴尺度集合预报试验(庄潇然等, 2017)。蔡沅辰等(2017)针对一次强对流天气, 基于不同随机物理模式扰动方案构造了混合模式扰动方案, 其预报准确率得到提升, 为进一步发展适用于风暴尺度集合预报系统的模式扰动技术提供理论依据。
相比传统集合预报, 对流尺度集合预报面临着以下问题:第一, 对流尺度天气系统时空尺度小, 高度非线性的特征决定了扰动的快速发展, 已有的扰动生成方法是否适用于对流尺度有待于进一步研究; 第二, 对流尺度天气系统局地性强必然要求较高的模式分辨率, 计算量增大带来如何建立高效的预报系统的问题; 第三, 传统生成集合预报结果的方法对于高分辨率、精细化要求的对流尺度集合预报不再适应。例如对于暴雨预报, 采用传统的集合平均方法往往会减弱降水强度, 因此需要引入生成适合对流尺度集合预报结果的方法。基于以上问题, 针对一次强飑线天气过程进行了集合预报试验, 采用BGM法生成初始扰动成员, 引入概率匹配平均法生成集合预报结果, 并通过偏差和公平技巧评分对降水过程进行了预报效果检验, 对对流尺度集合预报进行了初步的研究讨论。
2 个例介绍与方案设计2014年7月30日下午至31日凌晨, 我国江淮地区经历了一次大范围强对流天气过程。受此次天气过程影响, 河南、安徽、江苏等地遭受了雷雨、大风等短时强对流天气的袭击, 大风导致河南省大量房屋受损和倒塌并造成5人死亡, 江苏省部分地区由于暴雨导致局地出现严重内涝, 受灾严重。其中, 30日06:00(世界时, 下同)-11:00, 一条东西向的强飑线由北至南扫过苏、皖两省中北部, 明光市出现7级以上大风, 长丰庄局部地区出现暴雨, 1 h降水量达到75 mm。
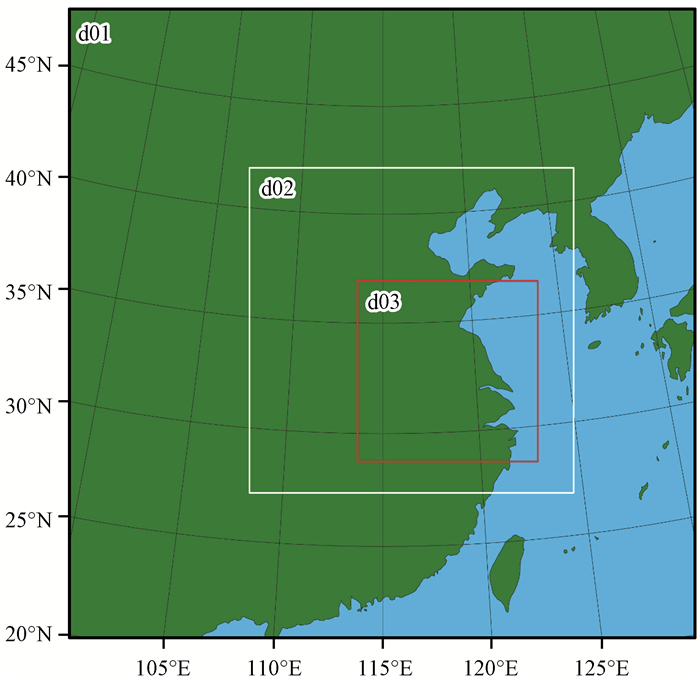
试验采用中尺度非静力模式WRFV3. 6版本, 模式设置为双向三重嵌套方案, 从2014年7月30日00:00起报, 预报时长为24 h, 区域设置如图 1所示。嵌套网格分辨率分别为18, 6和2 km, 母网格中心位于(35°N, 115°E), 格点数为175×175, 第二重网格d02格点数为271×271, 第三重网格d03格点数为451×451, 垂直层数42层。所有的集合成员均采用相同的物理参数化方案(用来研究初值扰动方案的预报效果)(表 1)。
|
图 1 WRF模式区域设置 Figure 1 The WRF model region settings |
| 表 1 基本物理参数化方案设置 Table 1 The basic physical parameter scheme settings |
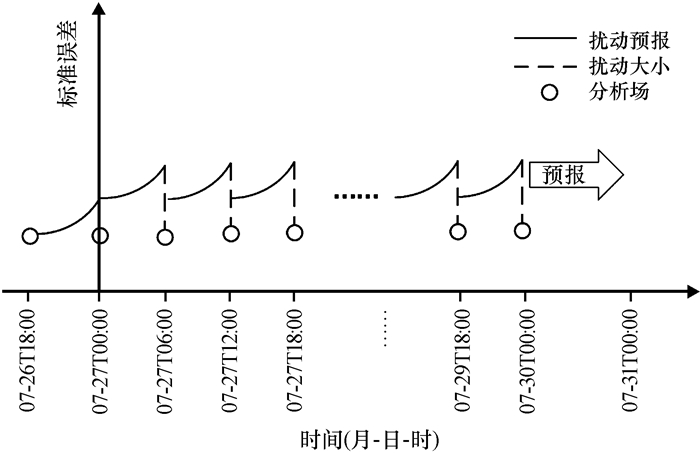
采用BGM法生成初始扰动成员进行集合预报试验。试验的培育阶段采用单层网格区域, 从7月27日00:00至30日00:00采用动态调整的方式共培育3天, 每6 h为一个培育周期, 设置10个集合成员, 具体流程如图 2所示。7月26日18:00开始向前预报6 h后得到预报均方根误差(RMSE), 计算公式为:
| $ RMSE = \sqrt {\frac{1}{{mn}}\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {{{\left[ {{\mathit{\Phi} _{F(i, {\rm{ }}j, {\rm{ }}k, {\rm{ }}t)}}{\rm{ - }}{\mathit{\Phi} _{O(i, {\rm{ }}j, {\rm{ }}k, {\rm{ }}t)}}} \right]}^2}} } }, $ | (1) |
|
图 2 2014年7月26日18:00至31日00:00初值扰动集合成员生成流程 Figure 2 The steps to generate ensemble members of initial perturbation from 18:00 on 26 to 00:00 on 31 July 2014 |
式中: m和n分别为研究区域纬向和经向格点数; ΦF(i, j, k, t)和ΦO(i, j, k, t)分别表示t时刻第k高度层上扰动变量的预报值和分析值。随后生成0~1范围内的随机数, 乘到均方根误差得到初始扰动dft。每经过一个培育周期时, 引入相应时刻的分析场, 采用动态调整(rescale)对当前得到的均方根误差进行尺度调整, 使其在均方根误差意义上与初始扰动保持同一量级。动态调整的方式为:
| $ d{f'_t} = \frac{{{e_0}}}{{{e_t}}}d{f_t}, $ | (2) |
式中: dft为经过一个培育周期后的扰动; et为对应时刻的均方根误差; e0为27日00:00的初始均方根误差; dft′为动态调整后的扰动。最后利用培育3天后得到的扰动构成初值扰动集合成员, 进行集合预报。
3 资料与方法采用NECP 1°×1°全球再分析资料驱动模式运行, 以江苏省气象台发布的江淮地区雷达资料和国家气象信息中心发布的0. 1°×0. 1°卫星融合降水资料作为实况进行对比。
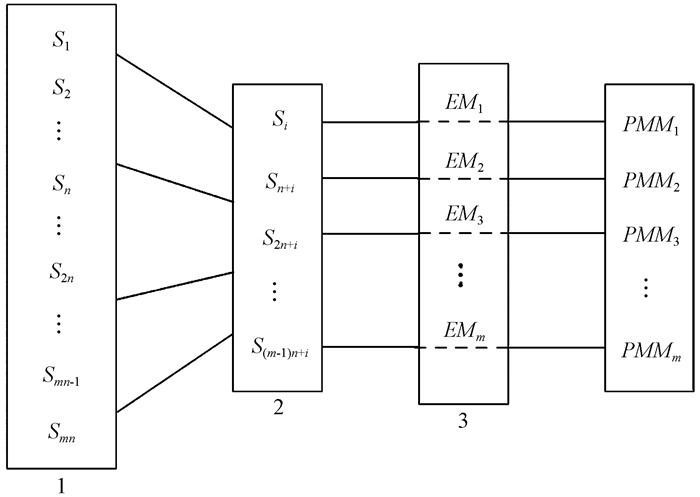
3.1 概率匹配平均法集合预报结果的传统处理方法为集合平均(Ensemble Mean, EM), 即对所有集合成员的预报结果进行简单平均。EM法虽然能够综合所有集合成员的信息, 但由于各个集合成员的扰动发展方向不同, 简单平均后一般会去除掉大量级的预报值, 导致预报强度偏低, 降低了集合预报对极端天气过程的预报能力。基于此, 采用概率匹配平均法(Probability Matched Mean, PMM)对集合成员预报结果进行综合处理(Ebert, 2001)。生成PMM序列的步骤如图 3所示, 其中: n为集合成员个数; m为预报区域内总格点数; S为格点预报值(指雷达最大反射率因子和降水量)。
|
图 3 PMM序列生成步骤 Figure 3 The generating steps of PMM sequence |
(1) 将所有集合成员在预报区域内所有格点上得到的预报值从大到小排列得到序列1;
(2) 从序列1中每隔n个选取一个预报值, 得到新的序列2, 该序列总个数和总格点数相同, 这样的序列2共有n种等概率情形, 随机选取第i个情形, 这里i=1, 2, 3, …, n-1, n。
(3) 计算每个格点j的算术平均EM值, 即
| $ E{M_j} = \frac{1}{n}\sum\limits_{k = 1}^n {{S_{k, {\rm{ }}j}}}, $ | (3) |
并将预报区域内所有格点按照EM值从大到小排列得到序列3。
(4) 从EM值最大的格点开始, 令序列2中Si为该格点的PMM值, 以此类推, 直至S(m-1)n+i为EM最小值所对应格点的PMM值, 从而得到PMM序列。
在这里序列3充当一个“桥梁”的作用, 提供给PMM序列各值所在的格点位置。特别地, 当EM=0时, 为保证PMM序列与集合平均场的结构一致, 取对应格点的PMM值为0。即序列2数值大小的空间格点分布与序列3 EM值大小的空间格点分布相同, 因此PMM序列和EM序列有着相同的空间分布形态。PMM值由序列2根据EM场的空间分布得到, 而序列2是根据所有集合成员格点预报值从大到小排序得到, 在对应格点上序列2的值是单个成员中最大的, 因此PMM值能够将单个成员产生的最大振幅保留下来。
该方法作为一种改进的集合预报方法, 考虑到对流尺度天气系统内部时空变化快的特征, 综合了所有集合成员的格点预报值, 能够包含各个量级的预报信息且重点关注大量级预报信息, 对各集合成员落区预报的位移误差起到平滑的作用, 同时还保证了传统集合平均场的基本结构(Kong et al, 2008; Clark et al, 2009; Berenguer et al, 2012; Schwarz et al, 2014)。
3.2 BIAS评分检验偏差评分(Bias score)主要用来衡量模式对某一量级降水的预报偏差, 该评分在数值上等于预报区域内满足某降水阈值的总格点数与对应实况降水总格点数的比值(Kong et al, 2008)。用来反映降水总体预报效果的检验方法。BIAS评分的计算公式为:
| $ BIAS = \frac{F}{O}, $ | (4) |
式中: F为预报区域内满足所需量级的降水总格点数; O为该区域内实况满足该量级的总格点数。当BIAS>1时, 表示预报结果较实况而言偏湿; 当BIAS < 1时, 表示预报结果较实况而言偏干; 当BIAS=1时, 则表示预报偏差为0, 即预报技巧最高。
3.3 ETS评分检验由于BIAS评分主要是用于衡量预报区域内满足某降水阈值的预报技巧, 并不能衡量降水的准确率, 因此还需引入公平技巧评分(Equitable Threat Score, ETS)用于衡量对流尺度集合预报的预报效果。ETS评分表示在预报区域内满足某降水阈值的降水预报结果相对于满足同样降水阈值的随机预报的预报技巧, 因此该评分有效地去除了随机降水概率对评分的影响, 相对而言更加公平、客观。ETS评分的具体计算公式(王雨等, 2007)如下:
| $ ETS = \frac{{{N_A} - R\left(a \right)}}{{{N_A} + {N_B} + {N_C} - R\left(a \right)}}, {\rm{ }} $ | (5) |
| $ R\left(a \right) = \frac{{\left({{N_A} + {N_B}} \right)\left({{N_A} + {N_C}} \right)}}{{{N_A} + {N_B} + {N_C} + {N_D}}}, $ | (6) |
式中: R(a)表示随机情况下可能正确预报的次数; NA、NB、NC、ND由表 2定义。NA表示“正确命中次数”; NB表示“虚报次数”; NC表示“漏报次数”; ND表示“正确拒绝次数”。根据定义, 如果ETS>0时, 表示对于某量级降水来说预报有技巧; 如果ETS≤0时则表示预报没有技巧; 如果ETS=1则表示该预报为完美预报。
| 表 2 降水的检验分类表 Table 2 The classification of precipitation verification |
多普勒天气雷达是监测强对流天气的重要手段之一, 每6 min一次的探测结果能够对强对流天气的演变做出准确地判断, 能提高强对流天气的预报预警能力。此次飑线过程从06:00形成后, 在徐州和亳州一线生成东西带状分布的对流单体群; 缓慢南压并逐渐加强, 08:00达到最强, 在宿迁和宿州一线形成“弓状”强回波带, 继续南压, 强度减弱, 11:00后回波带解体、对流单体分布范围较广且排列无规则, 整个过程历时5 h。
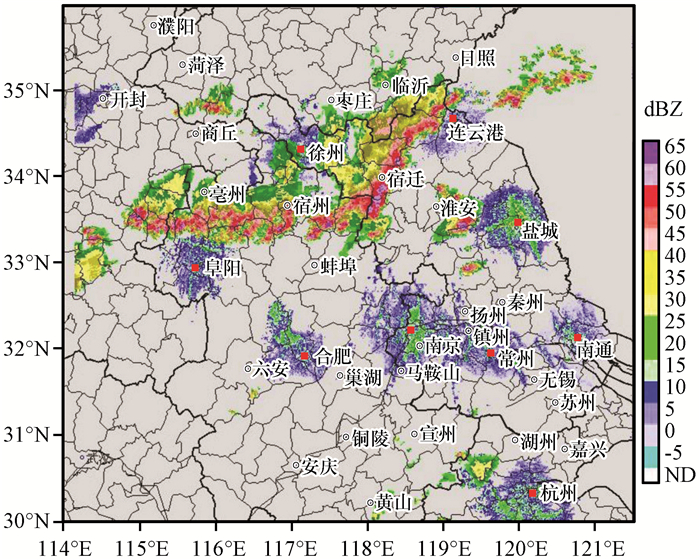
由2014年7月30日08:00江淮地区雷达1. 5°仰角的反射率拼图(图 4)可见, 一条狭窄的很多强回波块紧密排列组成的东西分布的雷暴带, 长度达到500 km。此强回波带中部在宿州附近有所分裂, 从强度上可大致分为两个发展阶段, 总体呈“弓状”分布。宿州东部的回波带在连云港和宿迁一线, 东北—西南走向, 回波带的前沿整齐且强度梯度大, 最大回波强度在宿迁附近, 达65 dBZ; 宿州西部的回波带在宿州和周口之间, 东西走向, 最大回波强度在50 dBZ以上, 强度小于东段回波带。
|
图 4 2014年7月30日08:00江淮地区雷达1. 5°仰角的反射率因子(单位: dBZ) Figure 4 The radar 1. 5 ° reflectivity factor in Jianghuai area at 08:00 on 30 July 2014. Unit: dBZ |
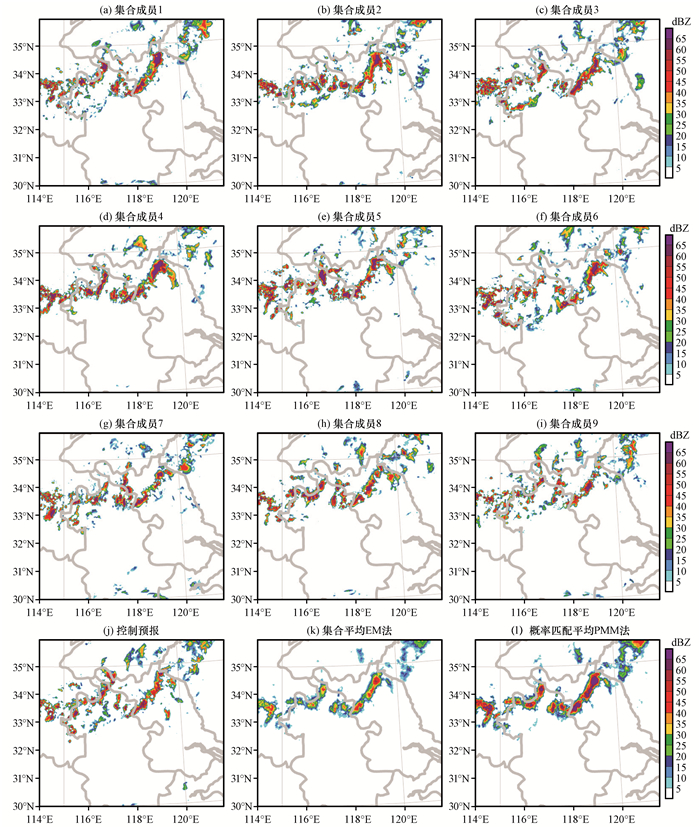
为了比较集合预报的预报效果, 图 5给出对应时刻的最大反射率因子分布, 与图 4实况进行对比。从雷达回波的分布范围可以看出, 此次试验能够较好地预报出强回波带所在的位置, 说明BGM法产生的扰动能够代表对流尺度上的不确定性, 但对于回波强度而言, 强回波带后部的弱回波区较实况来看预报的范围相对较小。对于东段回波带, 集合成员1, 3, 4和9, 控制预报, 集合平均和PMM法能够较好地预报出其强回波块排列紧密且前沿整齐的基本特征, 同时EM法和PMM法对该特征的预报效果最好, 要优于控制预报和单个集合成员的预报效果, 而其余集合成员预报强回波块的分布相对分散。从回波强度来看, 集合成员3, 4, 5和7预报的回波强度大于65 dBZ的区域比实况范围要大, 这对PMM法所得到的回波分布有着显著的影响, 原因在于PMM法包含了各回波强度量级的信息, 受到集合成员中回波强度较大成员的约束, 使得PMM法得到回波强度大于65 dBZ的区域比实况范围要大; 而EM法得到的最大回波强度在40~50 dBZ, 与实况相比小了大约5 dBZ, 这是因为对于高时空分辨率的对流尺度而言, EM法从数学上削弱了较大回波强度对其贡献。相比之下, 西段回波带的预报效果要稍微差些, 各集合成员预报的强回波块东西排列相对分散, 只有EM法和PMM法能够基本描述出其东西带状分布, 其预报效果要明显优于控制预报和单个集合成员。从回波强度上看, PMM法要比实况大5 dBZ左右, 而EM法预报的强度与实况最为接近, 可见集合平均对中等强度回波能够作出准确地预报。因此, 当回波强度较大时, 可用PMM法对集合成员结果进行综合, 以弥补EM法对极端强度预报能力较差的缺陷。
|
图 5 2014年7月30日08:00预报的最大反射率因子分布(单位: dBZ) Figure 5 The distribution of forecasted maximum reflectivity factor at 08:00 on 30 July 2014. Unit: dBZ |
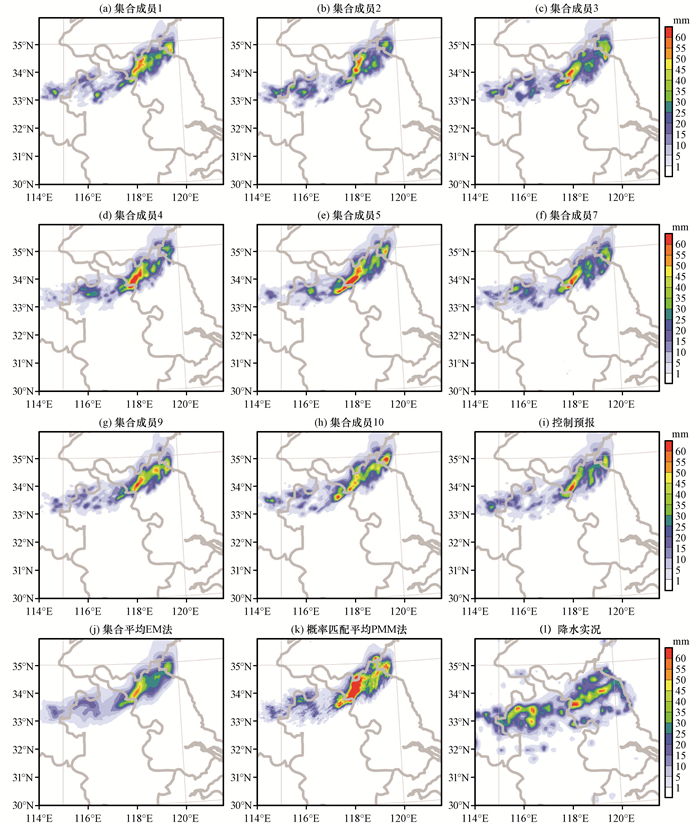
此次强对流天气过程降水重点时段为强飑线由北至南扫过苏、皖两省中北部的30日07:00-11:00的4 h, 为进一步比较集合预报的预报效果, 对预报07:00-11:00的4 h累计降水量分布进行分析(图 6)。从降水实况[图 6(l)]可以看出, 累计降水量同样呈东西向带状分布, 这与图 4的雷达回波形态和落区基本一致。同时降水中心和雷达回波带类似地可以分为东西两段, 东段有两个强降水中心, 分别位于宿迁和连云港附近, 其中宿迁地区的4 h累计降水量达到60 mm以上的暴雨量级; 西段的强降水中心降水量也达到了50 mm, 同样位置处于最大回波强度附近。从累计降水量的分布范围来看, 此次试验预报的落区东段稍稍偏北, 总体而言能够较好地预报出累计降水量的基本形态; 各个集合成员预报的落区十分相似, 这也反映出对流尺度集合预报的一个关键性问题, 如何保证集合成员的有效发散度。从降水强度来看, 对于东段降水而言, 集合成员2, 3, 7, 9和控制预报能够预报出宿迁附近的暴雨中心, 其中集合成员9较好地预报出了宿迁和连云港附近两个强降水中心, 而集合成员4和5预报的暴雨中心范围偏大, 集合成员10虚报了山东和江苏近海一个降水中心大于60 mm的暴雨中心, 这说明相比降水落区而言, 降水强度的集合成员发散度要大一些。集合平均很好地预报出两个强降水中心位置, 但降水强度上存在量级偏小10 mm的问题; 而PMM法对于降水中心的范围预报地明显偏大。相比东段降水, 西段降水落区分布相对分散, 降水强度预报偏弱, 这和雷达回波分布及强度同样存在东段优于西段的预报结果。对于西段降水, 相比集合成员和控制预报而言, 集合平均能够对于降水中心分布范围做出更加准确的预报, 而PMM法预报的降水强度与实况最为接近。
|
图 6 2014年7月30日07:00-11:00预报的4 h累计降水量分布(单位: mm) Figure 6 The distribution of 4 hours accumulated precipitation from 07:00 to 11:00 on 30 July 2014. Unit: mm |
此次强对流过程从30日06:00-19:00总共经历13 h, 其中07:00-11:00为飑线过程带来的最强降雨时段。为了进一步比较集合预报对不同量级降水的预报效果, 对预报07:00-11:00的4 h累计降水量和预报06:00-18:00的12 h累计降水量分别进行不同降水阈值的BIAS评分和ETS评分检验。
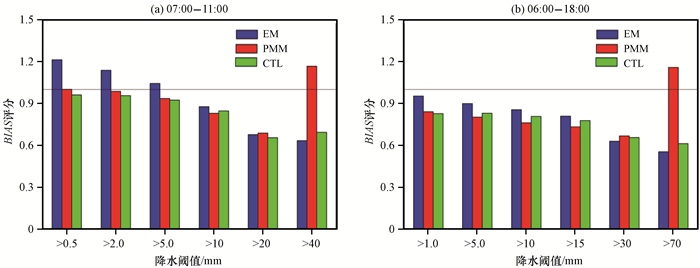
4.3.1 BIAS评分通过4 h和12 h累计降水量在不同降水阈值的BIAS评分柱状(图 7, BIAS=1用黑色实线标出)可以看出, 4 h累计降水量[图 7(a)]集合平均在降水阈值为0. 5~5. 0 mm的小量级降水偏差评分大于1, 总体预报结果偏湿, 在降水阈值为20~40 mm的大量级降水总体预报结果明显偏干, 而在降水阈值为10 mm的中等量级降水时预报技巧最高。PMM法在小量级降水的预报效果较好, 而在极端降水面前总体预报结果明显偏湿, 这与图 6(k)中PMM法的降水中心分布范围偏大是一致的, 原因在于PMM法受各集合成员中量级较大的影响。而控制预报的预报结果偏干, 并且降水量级越大预报结果越干。对比图 7(a)和图 7(b)可知, 在降水阈值为5. 0 mm及以下的小量级降水方面, EM法的BIAS评分较PMM法和控制预报减小明显, 集合平均的总体预报结果由偏湿变到偏干。并且从12 h累计降水量在不同降水阈值的BIAS评分[图 7(b)]还可以看出, 集合平均EM法较PMM法和控制预报在降水阈值为10 mm以下的小量级降水偏差评分接近1, 总体预报效果最好, 在大量级降水的总体预报结果明显偏干, 评分甚至低于控制预报, 而PMM法在降水阈值大于70 mm的大量级降水的偏差评分偏湿。
|
图 7 2014年7月30日4 h(a)和12 h(b)累计降水量在不同降水阈值的BIAS评分 Figure 7 The Bias score in different rainfall thresholds for the 4 (a) and 12 (b) hours accumulated precipitation on 30 July 2014 |
通过最强降水时段和天气过程总降水时段的累计降水量BIAS评分分析可知, PMM法对于短时极端降水过程预报偏差最小, 总体预报效果最好; 集合平均EM法对于总降水时段的预报偏差最小, 总体预报效果优于PMM法; 而EM法和PMM法在两类时段的总体预报效果均优于控制预报。
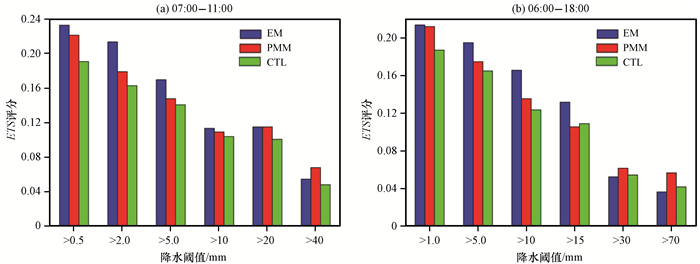
4.3.2 ETS评分从4 h和12 h累计降水量在不同降水阈值的ETS评分(图 8)的对比可知, 无论是EM法和PMM法还是控制预报, 预报技巧均随着降水量级的增大而减小, 这反映出模式系统长期存在对极端降水预报准确率较低的缺点。由4 h累计降水量在不同降水阈值的ETS评分[图 8(a)]可以看出, 小量级降水的预报技巧从高到低分别为EM法、PMM法、控制预报; 而PMM法在大量级降水的预报技巧上反超集合平均, 同时集合平均和PMM法的预报技巧始终都优于控制预报。由12 h累计降水量在不同降水阈值的ETS评分[图 8(b)]可以看出, 在小量级降水上集合平均的ETS评分最高, 而在大量级的降水上, PMM法的预报技巧要明显优于集合平均和控制预报。
|
图 8 2014年7月30日4 h(a)和12 h(b)累计降水量在不同降水阈值的ETS评分 Figure 8 The Equitable threat score in different rainfall thresholds for the 4 (a) and 12 (b) hours accumulated precipitation on 30 July 2014 |
ETS评分是对BIAS评分总体预报效果的进一步检验, 通过以上分析可知, ETS评分与BIAS评分的结果基本一致。集合平均在小量级降水的预报技巧上最高, PMM法在大量级降水的预报上有着明显的优势, 同时无论在何种量级降水的预报, EM法和PMM法的预报技巧均高于控制预报。
5 结论与讨论基于BGM法对一次强飑线天气过程进行对流尺度集合预报试验, 在培育阶段采用单层网格以降低计算成本, 预报阶段进行三重嵌套预报。考虑对流尺度高度非线性特征和精细化预报要求, 引入区别于传统集合平均的PMM法生成集合预报产品进行对比分析, 并通过BIAS和ETS评分进行降水检验, 得到如下结论:
(1) 将BGM法应用到对流尺度集合预报中能够生成代表大气不确定性的快速增长扰动, 试验很好地预报出飑线系统的位置和强度, 集合成员的预报结果起到一定的指示意义。单层培育的集合预报方案减少计算量的同时, 能够获得快速增长扰动作为预报阶段的初始分析场。
(2) 无论是雷达回波、降水强度和落区的预报, 还是降水的评分检验, 对流尺度集合预报的预报准确率大于控制预报, 对预报技巧有一定的提高作用。
(3) 通过雷达反射率和累计降水量分布的分析, 集合平均在较小强度的降水预报上更加准确, 但在大量级降水上的预报能力较低; 而PMM法在大量级降水上的预报能力明显优于集合平均EM法, 弥补了传统集合平均对极端天气事件预报技巧偏低的缺陷。
(4) 通过对累计降水量的评分检验可知, 集合平均在小量级降水的预报技巧上最高, 而PMM法在大量级降水的预报技巧上有着明显的优势, 这进一步说明PMM法在对流尺度集合预报中对强降水和极端天气有指示意义。
综上所述, 对流尺度集合预报仍存在集合成员发散度不高的问题亟待解决; 同时, 对流尺度集合预报的强局地性特点也要求通过大量的试验来确定适合不同地区的集合扰动方案, 这些问题需要进一步对对流尺度集合预报进行深入的研究, 以提高对流尺度集合预报对高影响对流天气事件的预报预警能力。
Berenguer M, Surcel M, Zawadzki I, et al. 2012. The diurnal cycle of precipitation from continental radar mosaics and numerical weather prediction models. Part Ⅱ:Intercomparison among numerical models and with nowcasting[J]. Mon Wea Rev, 140(8): 2689–2705.
|
|
Bishop C H, Toth Z. 1999. Ensemble transformation and adaptive observations[J]. J Atmos Sci, 56(11): 1748–1765.
DOI:10.1175/1520-0469(1999)056<1748:ETAAO>2.0.CO;2 |
|
Bishop C H, Etherton B J, Majumdar S J. 2001. Adaptive sampling with the ensemble transform Kalman filter. Part Ⅰ:Theoretical aspects[J]. Mon Wea Rev, 129(3): 420–436.
DOI:10.1175/1520-0493(2001)129<0420:ASWTET>2.0.CO;2 |
|
Clark A J, Gallus W, Xue M, et al. 2009. A comparison of precipitation forecast skill between small convection-allowing and large convection-parameterizing ensembles[J]. Wea Forecasting, 24(4): 1121–1140.
DOI:10.1175/2009WAF2222222.1 |
|
Clark A J, Weiss S J, Kain J S, et al. 2012. An overview of the 2010 hazardous weather testbed experimental forecast program spring experiment[J]. Bull Amer Meteor Soc, 93(1): 55–74.
DOI:10.1175/BAMS-D-11-00040.1 |
|
Ebert E E. 2001. Ability of a poor man's ensemble to predict the probability and distribution of precipitation[J]. Mon Wea Rev, 129(10): 2461–2480.
DOI:10.1175/1520-0493(2001)129<2461:AOAPMS>2.0.CO;2 |
|
Kong F, Xue M, Thomas K, et al, 2008. Real-time storm-scale ensemble forecast experiment -analysis of 2008 spring experiment data[C]//24th Conference on Several Local Storms, Amer Meteor Soc, Savannah.
|
|
Kong F, Xue M, Thomas K W, et al, 2009. A realtime storm-scale ensemble forecast system: 2009 spring experiment[C]//23th Conference on Weather Analysis and Forecasting and 19th Conference on Numerical Weather Prediction, Amer Meteor Soc, Omaha, Nebraska.
|
|
Lorenz E N. 1963. Deterministic nonperiodic flow[J]. J Atmos Sci, 20(2): 130–141.
DOI:10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2 |
|
Schwartz C S, Romine G S, Smith K R, et al. 2014. Characterizing and optimizing precipitation forecasts from a convection-permitting ensemble initialized by a mesoscale ensemble Kalman Filter[J]. Wea Forecasting, 29(6): 1295–1318.
DOI:10.1175/WAF-D-13-00145.1 |
|
Schwartz C S, Romine G S, Weisman M L, et al. 2015a. A real-time convection-allowing ensemble prediction system initialized by mesoscale ensemble Kalman Filter analyses[J]. Wea Forecasting, 30(5): 1158–1181.
DOI:10.1175/WAF-D-15-0013.1 |
|
Schwartz C S, Romine G S, Sobash R A, et al. 2015b. NCAR's experimental real-time convection-allowing ensemble prediction system[J]. Wea Forecasting, 30(5): 1645–1654.
|
|
Toth Z, Kalnay E. 1993. Ensemble forecasting at Nmc:the generation of perturbations[J]. Bull Amer Meteor Soc, 74(12): 2317–2330.
DOI:10.1175/1520-0477(1993)074<2317:EFANTG>2.0.CO;2 |
|
Toth Z, Kalnay E. 1997. Ensemble forecasting at NCEP and the breeding method[J]. Mon Wea Rev, 125(12): 3297–3319.
DOI:10.1175/1520-0493(1997)125<3297:EFANAT>2.0.CO;2 |
|
Xue M, Kong F, Weber D, et al, 2007. CAPS realtime storm-scale ensemble and high-resolution forecasts as part of the NOAA hazardous weather testbed 2007 spring experiment[C]//22th Conference on Weather Analysis and Forecasting and 18th Conference on Numerical Weather Prediction, Amer Meteor Soc, Park City, UT.
|
|
Xue M, Kong F, Thomas K W, et al, 2010. CAPS realtime storm scale ensemble and high resolution forecasts for the NOAA hazardous weather testbed 2010 spring experiment[C]//25th Conference on Several Local Storms, Amer Metor Soc, Denver, Colorado.
|
|
杜钧. 2002. 集合预报的现状和前景[J]. 应用气象学报, 13(1): 16–28.
Du J. 2002. Present situation and prospects of ensemble numerical prediction[J]. J Appl Meteor Sci, 13(1): 16–28.
|
|
蔡沅辰, 闵锦忠, 庄潇然. 2017. 不同随机物理扰动方案在一次暴雨集合预报中的对比研究[J]. 高原气象, 36(2): 407–423.
Cai Y C, Min J Z, Zhuang X R. 2017. Comparison of different stochastic physics perturbation schemes on a stormscale ensemble forecast in a heavy rain event[J]. Plateau Meteor, 36(2): 407–423.
DOI:10.7522/j.issn.1000-0534.2016.00024 |
|
高峰, 闵锦忠, 孔凡铀. 2010. 基于增长模繁殖法的风暴尺度集合预报试验[J]. 高原气象, 29(2): 429–436.
Gao F, Min J Z, Kong F Y. 2010. Experiment of the storm-scale ensemble forecast based on breeding of growing mode[J]. Plateau Meteor, 29(2): 429–436.
|
|
王晨稀, 姚建群. 2006. 上海区域数值预报模式集合预报系统的建立与试验[J]. 气象科学, 26(2): 127–134.
Wang C X, Yao J Q. 2006. The establishment and experiment of Shanghai regional numerical ensemble forecast system[J]. Scientia Meteor Sinica, 26(2): 127–134.
|
|
王晨稀, 姚建群. 2008. 对一次局地短时强降水过程的集合预报研究[J]. 高原气象, 27(6): 1299–1239.
Wang C X, Yao J Q. 2008. Ensemble forecasting of a local short-lived severe precipitation[J]. Plateau Meteor, 27(6): 1299–1239.
|
|
王雨, 闫之辉. 2007. 降水检验方案变化对降水检验评估效果的影响分析[J]. 气象, 33(12): 53–61.
Wang Y, Yan Z H. 2007. Effect of different verification schemes on precipitation verification and assessment conclusion[J]. Meteor Mon, 33(12): 53–61.
|
|
庄潇然, 闵锦忠, 蔡沅辰, 等. 2016. 不同大尺度强迫条件下考虑初始场与侧边界条件不确定性的对流尺度集合预报试验[J]. 气象学报, 74(2): 244–258.
Zhuang X R, Min J Z, Cai Y C, et al. 2016. Convective-scale ensemble prediction experiments under different large-scale forcing with consideration of uncertainties in initial and lateral boundary condition[J]. Acta Meteor Sinica, 74(2): 244–258.
|
|
庄潇然, 闵锦忠, 武天杰, 等. 2017. 风暴尺度集合预报中不同初始扰动的多尺度发展特征研究[J]. 高原气象, 36(3): 811–825.
Zhuang X R, Min J Z, Wu T J, et al. 2017. Development mechanism of multi-scale perturbation based on different perturbation methods in convection-allowing ensemble prediction[J]. Plateau Meteor, 36(3): 811–825.
DOI:10.7522/j.issn.1000-0534.2016.00049 |
 2018, Vol. 37
2018, Vol. 37
