2. 中国科学院大学, 北京 100049;
3. 中国科学院青藏高原地球科学卓越创新中心, 北京 100101
气温是气象要素的主要组成部分, 有着重要的地理学和生态学意义, 不仅是自然地域系统界线划分的关键指标, 还是陆面环境过程模拟的重要参数(Régnière, 1996; Hock, 2003; 李月臣等, 2014; 郭建平等, 2016; 周盼盼等, 2017)。由于纬度、海陆分布以及地势地貌与下垫面的特性不同, 造成气温资源在空间分布上有明显的区域差异(张洪亮等, 2002; 高世仰等, 2017; 张长灿等, 2017)。由于受到自然条件和经济成本的限制, 中国气象观测站在全国范围内呈东部密集, 西部稀疏的分布特征。在我国西部地势险峻的高山地区, 不仅气象观测台站稀少, 而且这些监测站多分布于距离城镇较近的峡谷区域, 所获取的温度数据并不能真实反映山区的实际气温分布情况(Cui et al, 2015), 广大无站区域的气温只能通过间接推算得出。国内外在气温空间插值研究方面形成了一系列成熟的方法, 主要基于统计学原理, 如克里格插值(Kriging), 反距离加权插值(Inverse Distance Weighted), 多项式内插法(Polynomial Interpolation)等。这些插值方法多适用于站点分布密度大、地势平坦区域, 对于地形复杂且站点稀少的区域, 气象要素空间插值精度结果往往并不理想, 严重制约了山区科学研究(刘志红等, 2008; 刘正佳等, 2012; 李月臣等, 2014; 谭剑波等, 2016)。
20世纪90年代以来, 气温精细空间化研究得到空前发展。以Anusplin专用空间插值软件为代表的区域精细化方法在国内外得到广泛应用(Hutchison, 1991; Hijmans et al, 2005; 刘志红等, 2008; 谭剑波等, 2016)。Anusplin是澳大利亚科学家Hutchinson基于薄盘样条理论编写了针对气候数据曲面拟合的专用插值方法, 该方法引入多个影响因子作为协变量, 根据最佳拟合效果自动确定模型系数, 且能同时进行多个表面的空间插值, 对于时间序列的气象数据空间插值非常适用(刘志红等, 2008; 谭剑波等, 2016; Hutchinson et al, 2013)。目前, 使用Anusplin软件进行气候数据插值应用的研究较多, Hijmans et al(2005)利用Anusplin构建了全球分辨率为1 km的50年气温数据集, 认为该方法得到的区域气温数据具有较好的空间连续性。钱永兰等(2010)使用1 667个全国加密站点进行气温插值分析, 从统计学角度得出了Anusplin插值方法的总体精度水平优于反距离加权插值法和克里格插值法。谭剑波等(2016)以地形起伏巨大的青藏高原东南缘为研究区, 分别采用Anusplin和Cokriging进行空间气温插值, 通过整体对比和站点交叉验证, 认为Anusplin在山区气温模拟的细节方面表现更加突出, 且精度较高。
利用Anusplin针对不同空间尺度(全球、全国、地区、流域)(刘志红等, 2006, 2008)和不同时间尺度(日、旬、月、年)(Hijmans et al, 2005; McKenney et al, 2006; 沈艳等, 2008; 钱永兰等, 2010)已开展大量研究工作, 研究表明, Anusplin在气温空间插值方面具有较好的表现, 且对于我国山区气温的插值具有较高精度。但关于利用该方法在不同时间尺度下气温插值精度的对比研究却很少, 特别是针对于我国山区, 在较大地形高差的自然环境背景条件下, 各个时间尺度间的气温数据插值精度是否存在差异, 若存在差异, 何种时间尺度的气温数据插值精度较高, 这些问题还没有得到解答。鉴于此, 选取我国地形起伏较大的横断山区作为研究区, 利用Anusplin对年尺度, 月尺度, 日尺度气温数据分布进行空间插值, 通过气象站点交叉验证方法, 对比分析各个时间尺度气温数据的插值精度水平, 并由此探讨气温数据时间分辨率的差异性对山区温度插值精度的影响, 为我国山区的区域气温应用研究提供参考依据。
2 研究区概况、资料选取和方法介绍 2.1 研究区概况研究区位于我国西南部横断山区。地理位置介于97°21′E-105°57′E, 26°58′N-34°51′N之间, 东西宽约960 km, 南北长约864 km, 面积约82.94×104 km2, 涵盖青藏高原东南缘, 四川盆地以及云贵高原部分区域。研究区内分布着高原、高山、丘陵、盆地等我国西南地区主要地貌类型, 海拔区间为191~7 115 m, 具有巨大的地势高差和复杂多变的地貌特征。文中所涉及的地图是基于国家测绘地理信息局标准地图服务网站下载的审图号为GS(2016)1665号中国地图制作, 底图无修改。
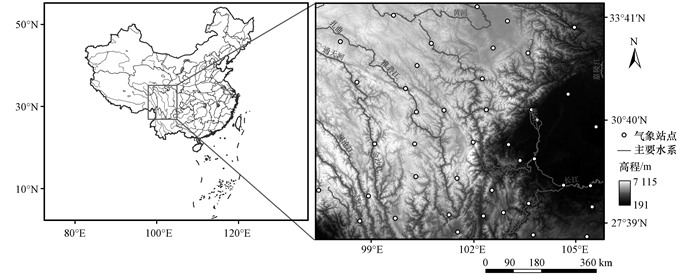
2.2 资料选取选用研究区51个气象站点(图 1)1960-2014年逐日气温资料, 数据来源于中国气象数据网(http://data.cma.cn), 原始信息包括台站号、经纬度、日平均温度、最高温度、最低温度。文章只提取日平均温度数据, 在提取数据过程中, 若存时间区间内异常数据或者缺测记录过多的站点, 则剔除。在完成数据质量控制的基础上, 计算获得研究区各个站点55年月平均气温、季节平均气温、年平均气温和年代平均气温, 其中, 季节数据包括:春季(3-5月)平均气温, 夏季(6-8月)平均气温, 秋季(9-11月)平均气温和冬季(12月至次年2月)平均气温。最后将研究区各个站点不同时间尺度的平均气温数据以Anusplin标准格式输出为*.txt文件。
|
图 1 研究区域气象站点分布 Figure 1 The distribution of meteorological stations in study area |
高程数据(图 1)来源美国地质勘探局数据共享网(https://earthexplorer.usgs.gov/)的SRTM3S, 坐标系WGS1984经纬度坐标, 利用Arcgis将DEM空间分辨率重采样为0.01°, 并将高程数据转成ASCLL格式, 作为协变量参与空间插值运算。
2.3 研究方法 2.3.1 空间插值方法薄盘光滑样条插值方法最早由Wahba于1979年提出, Hutchinson在1984年对其进行改进, 以适用于大数据集。后来又由Bates et al(1987)将其扩展为局部薄盘光滑样条法(Thomas, 2002; Hutchinson et al, 2013)。局部薄盘光滑样条法在插值过程中利用最优的光滑参数实现逼真度和光滑度最佳平衡, 保证了精度可靠, 同时允许引入线性协变量子模型, 如海岸线距离、海拔等多个地理因子作为线性协变量。局部薄盘光滑样条的理论统计模型为:
| $ {Z_i} = f\left({{x_i}} \right) + {b^T}{y_i} + {e_i}\;\;\;, \;\;\;\left({i = 1, 2, \cdots, n} \right) $ | (1) |
式中: Zi为位于空间i点的因变量; f(xi)为要估算关于xi的未知光滑函数, xi是独立变量; yi为独立协变量; b为独立协变量的系数; ei为随机误差。
Anusplin是基于局部薄盘样条光滑函数插值理论形成的一种较为成熟的气象要素插值工具, 且能同时进行多个表面的空间插值, 适用于时间序列的气象数据。利用Anusplin, 以SRTM高程数据作为协变量, 对近55年不同时间尺度下的气温数据进行空间插值。
2.3.2 精度评价方法采用站点观测数据交叉验证方法对不同时间尺度下的Anusplin插值结果进行精度评定。交叉验证就是随机地抽取部分观测站点作为验证站点, 用验证站点的观测结果去验证其余站点的插值结果, 比较该点的实际值和拟合值, 从而评价插值精度水平(谭剑波等, 2016; Kohavi, 1995)。将51个气象站点随机分为3组, 每组15个, 共得到45个验证站点。针对验证站点, 采用平均绝对误差(MAE)、平均相对误差(MRE)和均方根误差(RMSE)3个误差指标评估实际观测值与空间插值的精度差异。各误差指标的计算公式如下:
| $ MAE = \frac{1}{n}\sum\limits_{i = 1}^n {\left| {{Z_i} - {{Z'}_i}} \right|} \;\;, $ | (2) |
| $ MRE = \frac{1}{n}\sum\limits_{i = 1}^n {\left| {\frac{{{Z_i} - {{Z'}_i}}}{{{Z_i}}}} \right|} \;\;, $ | (3) |
| $ RMSE = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{\left({{Z_i} - {{Z'}_i}} \right)}^2}} } = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{\varepsilon ^2}} } \;\;\;, $ | (4) |
式中: Zi为第i个台站的观测值; Z′i为第i个站点的空间插值结果; n为随机抽取台站的个数。
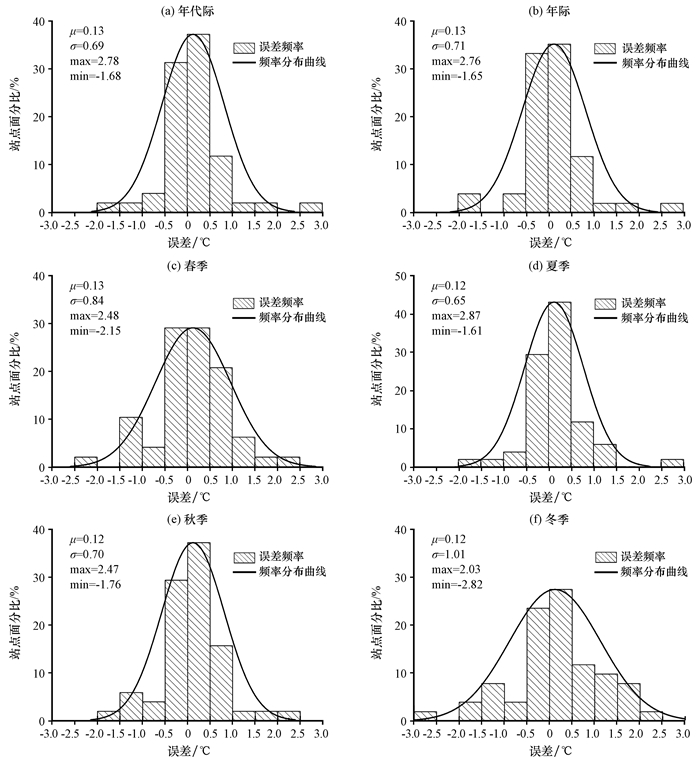
3 结果分析 3.1 年代际、年际和季节插值误差对比对研究区内不同时间尺度(年代际、年际和季节)插值结果进行误差统计, 从误差频率统计结果(图 2)可以看出, 研究区站点插值结果的绝对误差主要集中在±0.5 ℃以内, 且各个时间尺度下的误差频率分布数学期望μ值接近。在标准差σ方面, 各时间尺度插值结果表现不同, 其中, 年代、年、夏季和秋季误差频率分布的σ值相近, 表明插值结果误差分布离散度一致。此外, 春季插值结果误差分布的σ和冬季插值结果误差分布的σ较大, 其中冬季的σ最大, 为1.01, 表明冬季插值结果误差离散度最大。从误差范围来看, 春季和冬季的插值结果在负误差方向表现比其他时间尺度明显, 表明利用Anusplin对研究区春季和冬季气温数据插值时, 会更大概率出现低估的情况。
|
图 2 不同时间尺度插值结果误差频率分布 Figure 2 The frequency distribution of interpolation error at different time scales |
表 1为Anusplin在年代际, 年际和不同季节尺度下插值结果的误差对比。从表 1中可以看出, 在MAE和RMSE方面, 年代际插值结果与年际插值结果的精度水平一致, 并与四季中秋季的精度结果相近, 且分别低于春季和冬季, 表明年代际、年际以及秋季插值结果的绝对精度接近, 且分别高于春季和冬季插值结果的绝对精度。此外, 夏季插值结果的MAE和RMSE分别为0.41 ℃和0.66 ℃, 均低于年代际、年际、春季、秋季和冬季的误差值, 表明夏季插值结果具有最高的绝对精度; 在MRE方面, 冬季具有最大值0.81 ℃, 其次是春季, 为0.42 ℃, 秋季和年际的值接近, 分别为0.24 ℃和0.23 ℃, 夏季和年代际具有较小值, 分别为0.03 ℃和0.18 ℃, 说明在相对精度方面, 夏季具有最高相对精度水平, 其次是年代际。另外, 年际和秋季的精度水平相近, 春季和冬季具有较低相对精度, 其中冬季插值结果的相对精度最低。
| 表 1 不同时间尺度插值结果误差指标结果对比 Table 1 Error index of interpolation at different time scales |
分别利用研究区内站点实测气温数据和气象插值结果, 计算得到1960-2014年间年均气温和季节气温的年际变化率, 计算结果见表 2。
| 表 2 研究区不同时间尺度实测气温与插值气温年际变化率对比 Table 2 Comparison of temperature change rate calculated by the observation data and the inter at interpolation result at different time scales |
由表 2中可以看出, 利用Anusplin插值得到的气温结果, 在区域气候变化率描述方面表现良好, 在区域气候正负变化趋势方面, 插值结果与观测值所获得的年际变化趋势一致; 在绝对误差方面, 除了夏季和秋季具有较小误差[-0.09 ℃·(10a)-1和-0.04 ℃·(10a)-1]外, 年均气温, 春季气温以及冬季气温的插值结果年际变化率与站点实测值获得的年际变化率误差几乎为零。
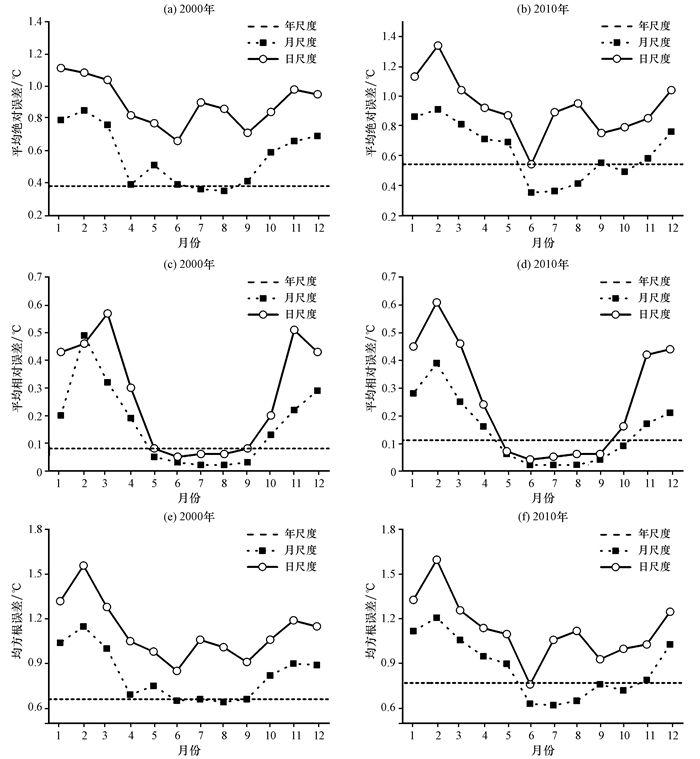
3.3 年内时间尺度插值精度对比上述研究是基于1960-2014年间年代际、年际以及季节尺度下55年内气温平均后所得到插值误差特征的对比结果, 为了排除数据平均对插值误差特征的影响, 分别选取2000年和2010年的年均气温, 各月均温以及日均温分别进行气象插值误差对比。通过2000年和2010年研究区年均温、月均温及日均温插值结果的各项误差指标(图 3)可以看出, 各月均温和各月日均温插值结果的各项误差指标从1-12月依次呈现先下降后上升的趋势。绝对精度方面, 研究区2000年和2010年各月日均温的平均绝对误差和均方根误差均呈现“W”型, 其中, 1月和2月达到全年最高值。各月均温的平均绝对误差和均方根误差在1月和2月达到全年最高值, 在6-8月达到全年低值; 相对精度方面, 各月均温和各月日均温的平均相对误差全年呈现“U”型, 在冬季月份达到误差高值, 在夏季月份达到误差低值。总体来看, 2000年和2010年研究区内各项误差指标全年呈现相同规律走势, 且各月日均温的精度误差高于各月均温的精度误差。此外, 部分月份(6-9月)月均温的平均绝对误差和均方根误差与年均温误差持平, 甚至略低于年均温误差, 表明绝对精度与年均温插值结果的精度水平一致或略优于年均温插值精度。同样在相对误差方面, 这些月份的月均温和月内日均温的误差值略低于年均温误差值, 表明相对精度水平略高于年均温插值的相对精度。
|
图 3 2000年和2010年不同时间尺度气象插值误差指标变化对比 Figure 3 The error index chart of annual, monthly and daily temperature in 2000 and 2010 |
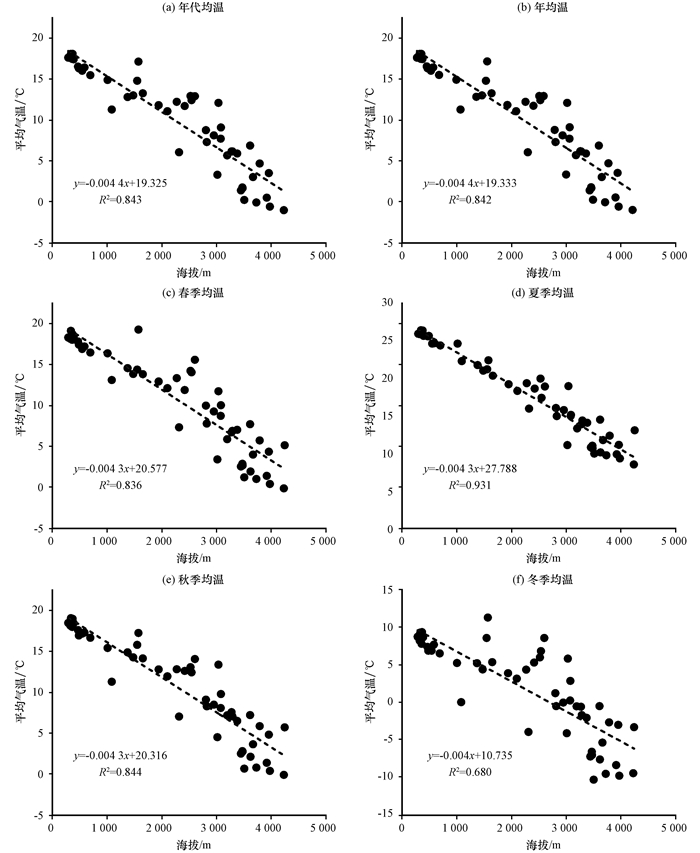
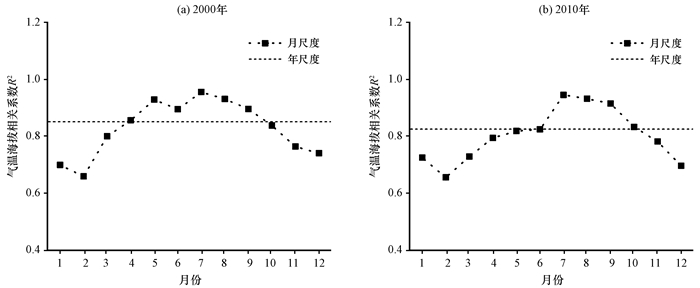
使用DEM作为协变量进行插值, 实际上是为Anusplin引入了高程线性子模型, 也就意味着利用这种方法得到的插值温度, 很大程度上依赖于气温随高程的变率。对研究区气象站点1969-2014年间的年代均温, 年均温, 春季均温, 夏季均温, 秋季均温和冬季均温分别与海拔进行统计分析(图 4), 发现各个时间尺度下的平均气温与海拔之间的线性拟合关系存在差异, 其中, 研究区夏季均温与海拔之间的线性拟合度最高, R2为0.931, 其余依次为是秋季均温, 年代均温, 年均温和春季均温, 冬季均温与气温海拔的拟合度最低, R2为0.680。图 5为2000年和2010年各月均温及年均温与海拔线性关系的统计结果。从图 5中可以看出, 夏季月份(6-8月)气温与海拔的拟合相关系数的值最高, 其次是秋季月份(9-11月)和春季月份(3-5月), 冬季月份(12月至次年2月)与海拔的拟合相关性最差。此外, 2000年和2010年的年均温海拔相关系数同春季和秋季月份的平均值基本持平, 该结论与图 3得到的结果一致, 表明研究区内气象站点夏季气温的海拔梯度性较稳定, 春季和秋季次之, 而冬季气温的海拔梯度性不明显。
|
图 4 1960-2014年间年代、年、季节气温随海拔梯度的变化 Figure 4 Decadal、annual and seasonal temperature in different elevation during 1960-2014 |
|
图 5 2000年和2010年各月均温及年均温海拔线性相关系数 Figure 5 The correlation coefficient between monthly temperature and altitude in 2000 and 2010 |
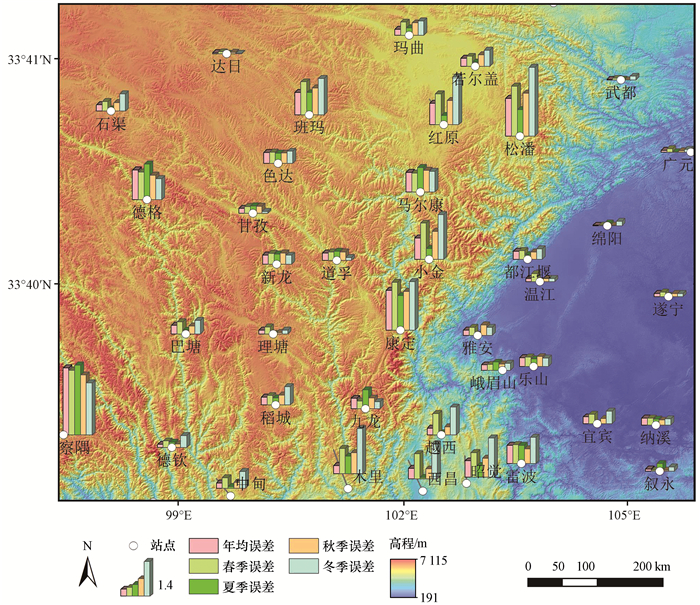
在气温插值误差空间分布方面(图 6), 误差较大的气象站点多数位于青藏高原东部的横断山区, 而位于横断山脉东部成都平原地区的气象站点各季节插值误差较小。从图 6中可以看出, 各个季节误差均较大的站点(察隅、康定、松潘、德格、斑玛、松潘、木里、雷波和小金)所处位置的SRTM海拔误差超过100 m(表 3), 其中察隅站点海拔误差高达711.4 m, 该站点各季节气温插值误差均高于其他站点误差。此外, 由于局地气候影响, 一些位于干温河谷站点(如松潘、小金和红原)和位于干热河谷站点(如越西、木里、西昌、昭觉和雷波)在季节气温方面表现出特殊性, 如春季和冬季气温明显高于同海拔的区域, 导致站点在该季节的气温严重低估(张一平等, 2004)。
|
图 6 研究区气象站点年均及季节均温插值误差空间分布 Figure 6 The cross-validation error of each point in annual and seasonal temperature |
| 表 3 高程误差超过100 m的站点 Table 3 The elevation error of these sites exceed 100 m |
选取我国地形起伏较大的横断山及周边区域作为研究区, 以研究区内51个国家气象站点1960-2014年日平均气温观测数据为基础资料, 以0.01°分辨率的SRTM数字地面高程作为协变量, 利用Anusplin插值方法对研究区不同时间分辨率(年代尺度, 年尺度, 季节尺度, 月尺度, 日尺度)气温数据进行空间插值, 通过气象站点交叉验证方法, 对比分析各个时间尺度气温数据的插值精度水平。研究发现利用Anusplin获得不同时间尺度气温的插值精度主要受气温海拔梯度性影响, 同时, DEM误差是造成Anusplin插值误差的主要原因, 而特殊的局地气候是造成季节性误差的原因之一。不同时间尺度气温插值精度情况如下:
(1) 年际时间尺度:夏季气温插值的绝对精度误差(MAE和RMSE)和相对精度误差(MRE)值最小, 分别为0.41, 0.66和0.03 ℃。年代、年均和秋季气温插值的绝对精度水平相近, 春季次之, 冬季气温插值的MAE, RMSE和MRE最大, 分别为0.79, 1.02和0.81 ℃。在区域气候变化趋势方面, 各个时间尺度气温插值数据的正负变化趋势和变化率与观测值结果一致。
(2) 年内时间尺度:各月均温和各月内日均温插值的各项误差从1-12月依次先下降后上升。绝对精度方面, 各月均温和各月内日均温的平均绝对误差和均方根误差在1月和2月达到全年最高值, 各月均温在6-8月达到全年低值, 且与年均温误差持平, 甚至略低于年均温误差; 相对精度方面, 各月均温和各月内日均温的平均相对误差全年呈现“U”型, 在冬季月份达到误差高值, 在夏季月份达到误差低值, 且误差值略低于年均温误差值。各月内日均温插值结果在绝对精度和相对精度方面均低于各月均温插值结果的精度水平。
基于Anusplin插值方法, 首次结合长时间序列气温数据进行多种时间尺度的空间插值精度验证, 且年际尺度精度验证与年内尺度精度验证所得结论相一致, 说明文章结果具有可靠性。此外, 插值误差原因分析分别从气温海拔梯度性、海拔误差以及局地气候背景展开讨论, 讨论内容能够合理解释不同时间尺度气温插值的精度差异性, 所得结论能够为山区气温插值的应用提供参考, 同时为基于Anusplin的高山区气温插值精度优化方法的研究提供理论依据。
Cui P, Jia Y. 2015. Mountain hazards in the Tibetan Plateau:research status and prospects[J]. National Science Review, 2(4): 397–399.
DOI:10.1093/nsr/nwv061 |
|
Hock R. 2003. Temperature index melt modelling in mountain areas[J]. J hydrol, 282(1): 104–115.
|
|
Hijmans R J, Cameron S E, Parra J L, et al. 2005. Very high resolution interpolated climate surfaces for global land areas[J]. Int J climatol, 25(15): 1965–1978.
DOI:10.1002/(ISSN)1097-0088 |
|
Hutchinson M F. 1991. The application of thin-plate smoothing splines to continent-wide data simulation[J]. BMRC Res Rep Ser: 28.
|
|
Hutchinson M F, Xu T. 2013. Anusplin version 4.4 user guide[M]. Canberra: The Australian National University.
|
|
Kohavi R, 1995. A study of cross-validation and bootstrap for accuracy estimation and model selection[C]//Ijcai, 14(2): 1137-1145.
|
|
McKenney D W, Pedlar J H, Papadopol P, et al. 2006. The development of 1901-2000 historical monthly climate models for Canadaand the United States[J]. Agricultural and Forest Meteorology, 138(1): 69–81.
|
|
Régnière J. 1996. Generalized approach to landscape-wide seasonal forecasting with temperature-driven simulation models[J]. Environmental Entomology, 25(5): 869–881.
DOI:10.1093/ee/25.5.869 |
|
Thomas A. 2002. Seasonal and spatial variation of evapotranspiration in the mountains of Southwest China[J]. J Mount Res, 20(4): 385–393.
|
|
郭建平, 刘欢, 安林昌, 等. 2016. 2001-2012年青藏高原积雪覆盖率变化及地形影响[J]. 高原气象, 35(1): 24–33.
Guo J P, Liu H, An L C, et al. 2016. Study on variation of snow cover and its orographic impact over Qinghai-Xizang Plateau during 20012012[J]. Plateau Meteor, 35(1): 24–33.
DOI:10.7522/j.issn.1000-0534.2014.00140 |
|
高世仰, 张杰, 罗琦. 2017. 青藏高原非均匀下垫面热力输送系数的估算[J]. 高原气象, 36(3): 596–609.
Gao S Y, Zhang J, Luo Q. 2017. Estimation of the heat transfer coefficient over inhomogeneous underlying surface on the Qinghai-Tibetan Plateau[J]. Plateau Meteor, 36(3): 596–609.
DOI:10.7522/j.issn.1000-0534.2016.00060 |
|
李月臣, 何志明, 刘春霞. 2014. 基于站点观测数据的气温空间化方法评述[J]. 地理科学进展, 3(8): 1019–1028.
Li Y C, He Z M, Liu C X. 2014. Review on spatial interpolation methods of temperature data from meteorological stations[J]. Progress in Geography, 3(8): 1019–1028.
DOI:10.11820/dlkxjz.2014.08.002 |
|
刘志红, 杨勤科, 李锐, 等. 2008. 基于ANUSPLIN的时间序列气象要素空间插值[J]. 西北农林科技大学学報(自然科学版), 36(10): 227–234.
Liu Z H, Yang Q K, Li R, et al. 2008. Interpolation for time series of meteorological variables using ANUSPLIN[J]. Journal of Northwest A & F University(Nat.Sci.Ed.), 36(10): 227–234.
|
|
刘志红, 杨勤科, 李锐, 等. 2006. 基于5变量局部薄盘光滑样条函数的蒸发空间插值[J]. 中国水土保持科学, 4(6): 23–30.
Liu Z H, Yang Q K, Li R, et al. 2006. Modeling spatial distribution of pan evaporation based on quinat-variate thin plate spline function[J]. Science of Soil and Water Conservation, 4(6): 23–30.
|
|
刘正佳, 于兴修, 王丝丝, 等. 2012. 薄盘光滑样条插值中三种协变量方法的降水量插值精度比较[J]. 地理科学进展, 31(1): 56–62.
Liu Z J, Yu X X, Wang S S, et al. 2012. Comparative analysis of three covariates methods in Thin-plate smoothing splines for interpolating precipitation[J]. Progress in Geography, 31(1): 56–62.
DOI:10.11820/dlkxjz.2012.01.008 |
|
钱永兰, 吕厚荃, 张艳红. 2010. 基于ANUSPLIN软件的逐日气象要素插值方法应用与评估[J]. 气象与环境学报, 26(2): 7–15.
Qian Y L, Lü H Q, Zhang Y H. 2010. Application and assessment of spatial interpolation method on daily meteorological elements based on ANUSPLIN software[J]. J Meteor Environ, 26(2): 7–15.
|
|
沈艳, 熊安元, 施晓晖, 等. 2008. 中国55年来地面水汽压网格数据集的建立及精度评价[J]. 气象学报, 66(2): 283–291.
Shen Y, Xiong A Y, Shi X H, et al. 2008. Development of the grid-based ground water vapor pressure over China in recent 55 years and its accuracy evaluation[J]. Acta Meteor Sinica, 66(2): 283–291.
DOI:10.11676/qxxb2008.027 |
|
谭剑波, 李爱农, 雷光斌. 2016. 青藏高原东南缘气象要素Anusplin和Cokriging空间插值对比分析[J]. 高原气象, 35(4): 875–886.
Tan J B, Li A N, Lei G B. 2016. Contrast on ANUSPLIN and Cokriging meteorological spatial interpolation in southeastern margin of Qinghai-Xizang Plateau[J]. Plateau Meteor, 35(4): 875–886.
DOI:10.7522/j.issn.1000-0534.2015.00037 |
|
张洪亮, 邓自旺. 2002. 基于DEM的山区气温空间模拟方法[J]. 山地学报, 20(3): 360–364.
Zhang H L, Deng Z W. 2002. A method of spatial simulating of temperature based digital elevation model(DEM) in mountain area[J]. J Mount Sci, 20(3): 360–364.
|
|
张一平, 张昭辉, 何云玲. 2004. 岷江上游气候立体分布特征[J]. 山地学报, 22(2): 179–183.
Zhang Y P, Zhang S H, He Y L. 2004. Distribution of climatic elements in the upper reaches of Minjiang river[J]. J Mount Sci, 22(2): 179–183.
|
|
张长灿, 李栋梁, 王慧, 等. 2017. 青藏高原春季地表感热特征及其对中国东部夏季雨型的影响[J]. 高原气象, 36(1): 13–23.
Zhang C C, Li D L, Wang H, et al. 2017. Characteristics of the surface sensible heat on the Qinghai-Xizang Plateau in the spring and its influences on the summertime rain fall pattern over the eastern China[J]. Plateau Meteor, 36(1): 13–23.
DOI:10.7522/j.issn.1000-0534.2016.00028 |
|
周盼盼, 张明军, 王圣杰, 等. 2017. 高亚洲地区夏季0℃层高度变化及其影响特征研究[J]. 高原气象, 36(2): 371–383.
Zhou P P, Zhang M J, Wang S J, et al. 2017. Variation and its influences of 0℃ isotherm height in summer over high Asia[J]. Plateau Meteor, 36(2): 371–383.
DOI:10.7522/j.issn.1000-0534.2016.00048 |
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. CAS Center for Excellence in Tibetan Plateau Earth Sciences, Beijing 100101, China
 2018, Vol. 37
2018, Vol. 37
