2. 高原与盆地暴雨旱涝灾害四川省重点实验室, 四川 成都 610072
浅层滑坡常发生于覆盖松散土层的陡峭山区, 由强降水、地震、地下水位变化、河流侵蚀和人类活动等外部因素导致的坡面材料剪应力和抗剪强度的变化引起, 在一定条件下可转变为破坏性更强的泥石流。李兆平等(2001)将降雨诱发边坡失稳的原因归结为土体抗剪强度随土体含水量降低、下渗降水降低潜在滑面的抗滑能力及渗流力作用等三个方面。目前关于浅层滑坡预测的研究主要分为三种:经验模型、统计模型和动力模型。以往根据实时和预报降水预测滑坡的研究多应用基于滑坡和降雨历史数据的统计方法, 该方法较少考虑地质条件及地形、水文等环境因素的影响, 难以判断滑坡具体发生的时间与位置。动力模型通过分析降雨入渗的过程对土体基质吸力、土体的应力状态和土体形变的影响, 研究降水过程带来的边坡稳定性变化。与经验模型相比, 动力模型能够解释滑坡发生的内部机理, 直观地表现不同降雨过程对边坡稳定性的影响。
TRIGRS(Transient Rainfall Infiltration and Grid-Based Regional Slope-Stability)模型(Baum et al, 2008)通过计算饱和及非饱和条件下均匀介质中的一维垂直渗流过程(Iverson, 2000; Srivastava et al, 1991)得到土体压力水头的变化, 并借助无限边坡模型计算边坡安全系数。模型适用于复杂地形环境与降水过程下安全系数的计算, 结果可直观地表现研究区域边坡安全性的空间分布与时间变化。陈则佑等(2011)、陈悦丽等(2016)、Dongyeob et al(2010)、Diana et al(2006)和Park et al(2013)的研究表明, TRIGRS模型在模拟大范围的边坡稳定性变化时具有较好的效果, 计算中可结合研究区实际情况对参数进行合理假设。
研究区域四川省广元市位于四川盆地西北部, 摩天岭中山区向龙门山中低山区及丘陵地带过渡区, 地处大巴山暴雨区内, 其中旺苍县为该区域暴雨中心之一。崩塌、滑坡及泥石流灾害主要发生在青川小区, 龙门山—大巴山分区及四川盆地分区地层。根据张英平等(2011)的研究结果, 广元市地质灾害点多集中在高程800 m以上的陡坡或陡崖部位, 主要沿龙门山断裂带、嘉陵江水系和交通线呈线状或带状分布, 其中滑坡为优势灾种。地质灾害潜在隐患点在天然状态下稳定或基本稳定, 但在饱水(持续暴雨)状态下转变为不稳定。
降水是边坡稳定性的重要影响因子, 利用预报降水数据驱动响应能力较好的边坡稳定性模型(杨星等, 2016), 可得出这一区域边坡稳定性在预报降水数据时段内的变化, 从而实现浅层滑坡预测。本文应用TRIGRS模型模拟四川省广元市2010年“7·23”暴雨过程中边坡稳定性变化, 将模拟结果与实际滑坡记录进行对比, 检验研究区域内边坡稳定性变化对降水的响应, 探讨模型应用于降雨型浅层滑坡预测的可行性。
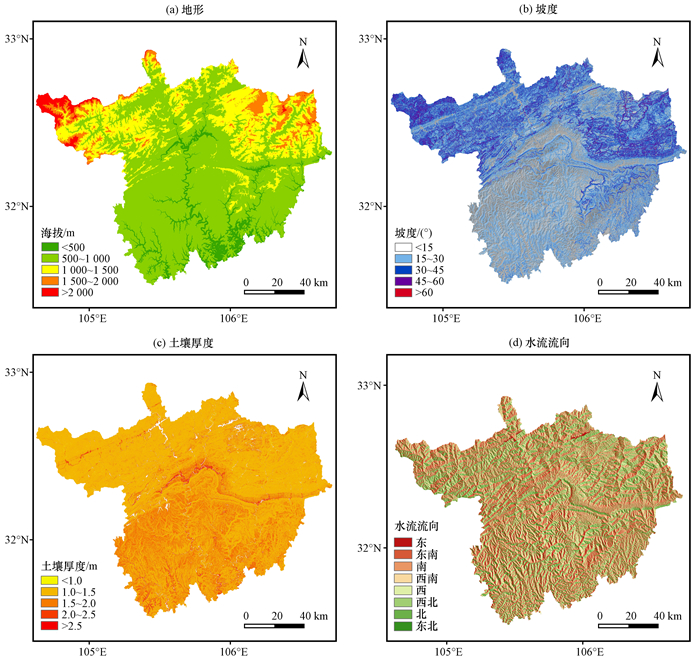
2 研究区域概况研究区位于川陕甘交界处, 地貌形态为北高南低, 北部青川、旺苍等县属高山地貌, 向南逐渐过渡为低山区地貌。位于龙门山构造断裂带北端, 受龙门山和摩天岭多期构造运动共同作用, 岩石节理裂隙发育, 岩层较为破碎, 较易发生崩塌和滑坡, 属地质灾害高发区(温克刚等, 2006)。地形以丘陵山地为主, 海拔自北向南逐渐降低, 其中最高点海拔为3 813 m, 位于研究区西北部青川县境内; 最低点海拔为326 m, 位于研究区东南部苍溪县境内[图 1(a)]。坡度在0°~80°之间, 北部高山地貌区集中分布在30°~45°区间内, 而南部低山地貌区集中分布在0°~30°区间内[图 1(b)]。北部高山地貌区土壤平均厚度小于南部低山地貌区, 海拔较高的山岭地区土层较薄, 海拔较低的河谷地区土层较厚[图 1(c)]。图 1(d)为利用单流向法计算的研究区域水流流向分布, 用于模拟地表径流产生过程。研究区域多年平均年降水量1 000~1 200 mm, 月降水量最大值出现在7月。平均年降水日数在120~140天, 年平均暴雨日数在4~7天, 暴雨的多发时间在下半夜至次日上午(马振峰等, 2016)。文中所涉及的地图均基于四川省标准地图服务网站下载的审图号为图川审(2016)018号的标准地图制作, 底图无修改。
|
图 1 研究区域地形(a)、坡度分布(b)、土壤厚度分布(c)及水流流向(d) Figure 1 Topographic (a), slope angle distribution (b), soil thickness distribution (c) and flow directions (d) of the study area |
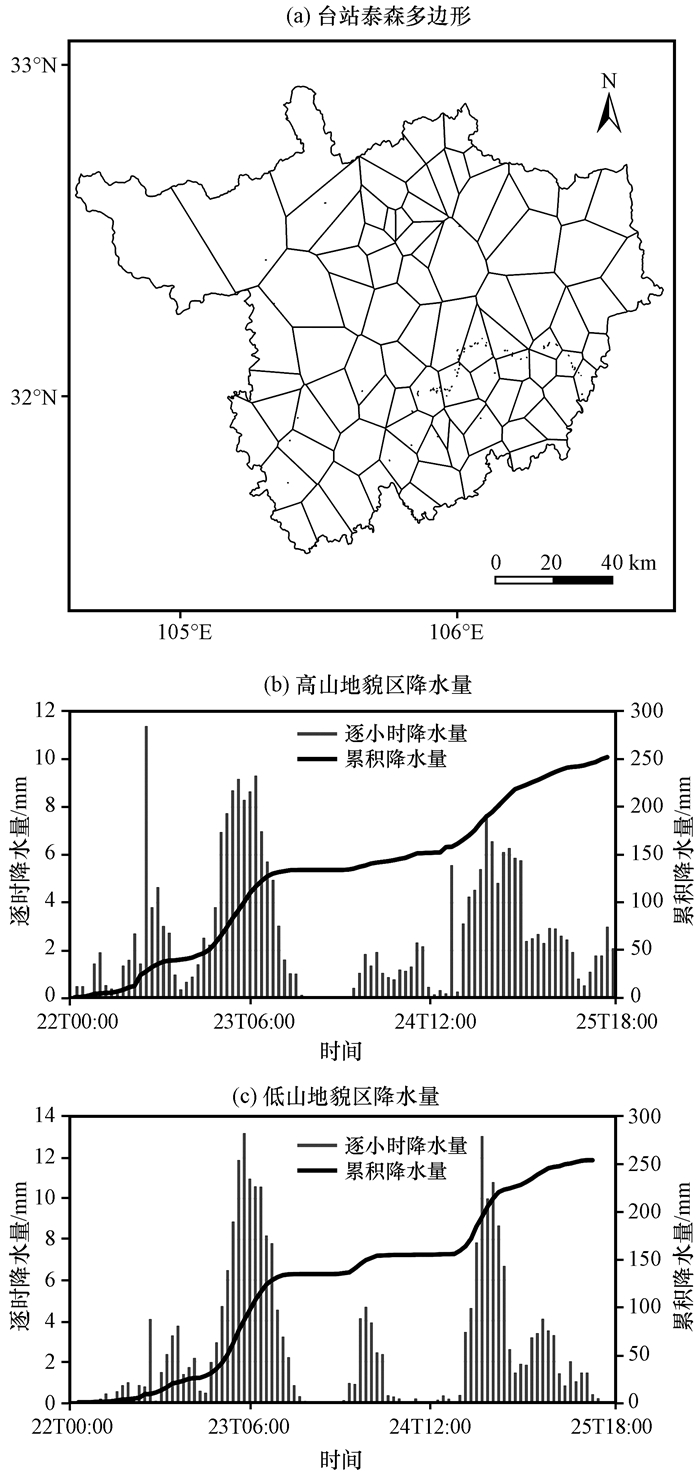
广元境内86个雨量站的逐时观测资料显示, 在2010年广元“7·23”特大暴雨过程前3天内, 广元各区域都曾出现零星降水, 土体趋于饱和; 图 2(b)与(c)为基于雨量站点泰森多边形分布计算的研究区面雨量历时曲线, 通过分析可知主要降水过程从7月22日早晨开始, 在13:00 (北京时, 下同)左右出现第一个峰值, 此时单站6 h累计雨量最高值为49.3 mm, 出现在广元北部; 此后夜间降水减少, 至23日04:00-09:00出现第二个高峰, 峰值面雨量为10.4 mm·h-1, 单站6 h累计雨量最高值为117.5 mm, 出现在广元西部; 23日下午至24日夜间降水较少, 25日02:00-05:00出现第三个降水高峰, 峰值面雨量为9.3 mm·h-1, 单站6 h累计雨量最高值为165.4 mm, 出现在广元西南部。
|
图 2 研究区雨量站泰森多边形(a)及高山地貌区(b)和低山地貌区(c)的逐时降水量及累积降水量 Figure 2 Voronoi diagram of the study area (a) and hourly rainfall and rainfall accumulation of mountain area (b) and hilly area (c) |
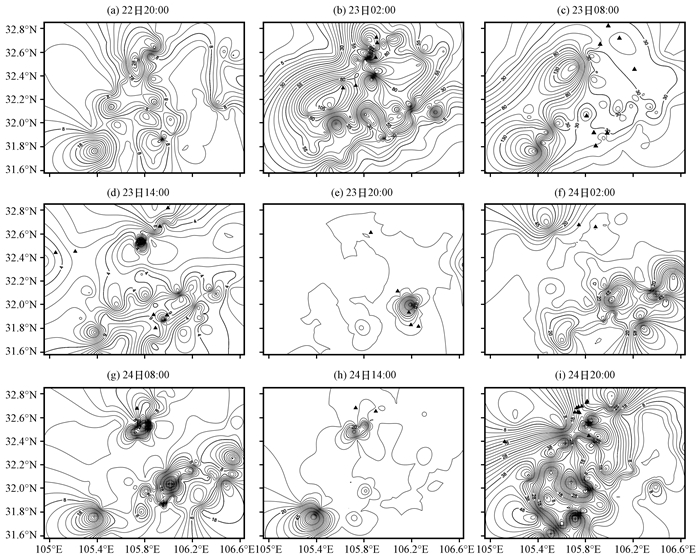
图 3为研究区从7月22日20:00开始6 h时间间隔累积地面降水。从图 3中可以看到, 研究区内降水分布较均匀, 主要的降水中心位于西北部和东南部。其中东部降水范围在0~150 mm, 西部降水范围在0~70 mm, 总体降水量呈西多东少, 北多南少的趋势。6 h累积降雨量最大值出现在23日早晨, 随后在下午至夜间减小, 夜间出现该过程中6 h累积降雨量最小值, 24日凌晨起降水再度增大, 一直持续至25日下午。本次降水过程共造成研究区域内出现有记录的滑坡38处, 崩塌2处, 地裂缝3处, 主要集中于研究区域北部和东南部; 造成2人死亡, 2人受伤, 直接经济损失达一千万元以上。
|
图 3 2010年7月22日20:00至24日20:00研究区域6 h时间间隔累积地面降水分布(单位: mm)三角符号表示相应时段发生滑坡的地点 Figure 3 Every 6 h rainfall accumulation distribution and landslide sites (triangle symbols) of study area from 20:00 on 22 to 20:00 on 24 July 2010. Unit: mm |
TRIGRS模型为美国地质调查所开发的基于栅格的降雨诱发型斜坡稳定性计算模型, 由斜坡稳定性计算模块、入渗模块和水文模块组成, 可计算降雨影响下的瞬态边坡安全系数。TRIGRS模型针对研究区域不同土壤初始情况提供了两种入渗模块, 其中应用于饱和或近饱和土壤条件下的模块基于Richard方程的线性形式建立(Baum et al, 2008; Iverson, 2000; Srivastava et al, 1991), 饱和土壤中渗流速度与水力坡降的关系符合线性渗流定律。本实验中, 由于试验区域前期存在零星降水, 土壤呈饱和至近饱和状态, 因此选用饱和土壤状态下入渗模块。
模型中边坡稳定性的计算采用适用于浅层滑坡的无限边坡稳定性分析(Iverson, 2000), 安全系数FS(Factor of Safety)定义为土块下滑阻力与动力的比值, 在深度Z上的计算方程为:
| $ FS = \frac{{\tan \phi '}}{{\tan \alpha }} + \frac{{c' - \psi (Z, t){\gamma _w}\tan \varphi '}}{{{\gamma _s}{d_{lb}}\sin \alpha \cos \alpha }}, $ | (1) |
式中: ϕ′为土壤内摩擦角; c′为土壤凝聚力; ψ为在时间t时土壤深度Z处的压力水头; dlb为不透水下边界所在深度; γw和γs分别为水和土壤的容重。无限边坡在FS>1时是稳定的。极限平衡条件下FS≤1代表边坡失稳。因此, 在时间t时图层中安全系数首先下降至1的深度即为滑坡发生的深度。
TRIGRS的入渗模块是基于线性渗流定律在无限深不透水下边界与瞬时地面径流情景下的解析(Iverson, 2000; Srivastava et al, 1991)建立。这一解析过程归纳如下:
| $ \begin{array}{l} \frac{{\partial \psi }}{{\partial t}}\frac{{{\rm{d}}\mathit{\Theta }}}{{{\rm{d}}\psi }} = \frac{\partial }{{\partial x}}\left[ {{K_L}(\psi)\left({\frac{{\partial \psi }}{{\partial x}} - \sin \alpha } \right)} \right]\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + \frac{\partial }{{\partial y}}\left[ {{K_L}(\psi)\left({\frac{{\partial \psi }}{{\partial y}}} \right)} \right]\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + \frac{\partial }{{\partial z}}\left[ {{K_Z}\left({\frac{{\partial \psi }}{{\partial z}} - \cos \alpha } \right)} \right], \end{array} $ | (2) |
式中: ψ为压力水头; Θ为体积含水量; α为坡度; KL与KZ分别为水平和垂直方向上的水力扩散度。
只考虑一维垂直渗流过程的情况下, 式(2)可简化为:
| $ \frac{{{\rm{d}}\mathit{\Theta }}}{{{\rm{d}}\psi }} = \frac{\partial }{{\partial z}}\left[ {{K_Z}(\psi)\left({\frac{{\partial \psi }}{{\partial z}} - \cos \alpha } \right)} \right], $ | (3) |
假设土体处于饱和状态, 定义K0为饱和水力传导度, C0为恒定容水度, 式(2)可写为:
| $ \frac{{\partial \psi }}{{\partial t}} = {D_0}\left({\frac{{{\partial ^2}\psi }}{{\partial {x^2}}} + \frac{{{\partial ^2}\psi }}{{\partial {y^2}}} + \frac{{{\partial ^2}\psi }}{{\partial {z^2}}}} \right), $ | (4) |
式中: D0=K0/C0; 容水度C=dΘ/dψ。式(4)用于计算在土壤张力饱和, 即土壤含水量和水力扩散度都可视为常数情况下的瞬时径流。计算一维垂直方向上的渗流时可写为:
| $ \frac{{\partial \psi }}{{\partial t}} = {D_1}\frac{{{\partial ^2}\psi }}{{\partial {Z^2}}}, $ | (5) |
式中: D1=D0/cos2α, 坡面法线坐标系与垂直坐标系的转换方程为Z=z/cosα, α为坡度。
式(5)的解析可用于计算在地面上和在深度为dlb的不透水下边界处随时间变化的特定流量边界条件(Savage et al, 2003, 2004)。在TRIGRS程序中该解析的应用形式为:
| $ \begin{array}{l} \psi \left({Z, {\rm{ }}t} \right) = (Z - {d_{wt}})\beta + 2\sum _{n = 1}^N\frac{{{I_{nZ}}}}{{{K_Z}}}H(t - {t_n})\sqrt {{D_1}(t - {t_n})} \\ \sum _{m = 1}^\infty \left\{ {{\rm{ierfc}}\left[ {\frac{{\left({2m - 1} \right){d_{lb}} - ({d_{lb}} - Z)}}{{2\sqrt {{D_1}(t - {t_n})} }}} \right]} \right.\\ \left.{ + {\rm{ierfc}}\left[ {\frac{{\left({2m - 1} \right){d_{lb}} - ({d_{lb}} - Z)}}{{2\sqrt {{D_1}(t - {t_n})} }}} \right]} \right\}{\rm{ }}\\ - 2\sum _{n = 1}^N\frac{{{I_{nZ}}}}{{{K_Z}H}}(t - {t_{n + 1}})\sqrt {{D_1}(t - {t_{n + 1}})} \\ \cdot\sum _{m = 1}^\infty \left\{ {{\rm{ierfc}}\left[ {\frac{{\left({2m - 1} \right){d_{lb}} - ({d_{lb}} - Z)}}{{2\sqrt {{D_1}(t - {t_{n + 1}})} }}} \right]} \right.\\ \left.{ + {\rm{ierfc}}\left[ {\frac{{\left({2m - 1} \right){d_{lb}} - ({d_{lb}} - Z)}}{{2\sqrt {{D_1}(t - {t_{n + 1}})} }}} \right]} \right\}, \end{array} $ | (6) |
式中: ψ为压力水头; t为时间; dwt为Z方向上的稳态地下水深度。InZ为第n时间间隔内的地面流量; dlb为Z方向上的土壤层厚度; N为时间间隔数; H(t-tn)为单位阶跃函数。β=λcosα, 其中: λ=cosα-(IZ/KZ)LT, 表示Z方向上的稳态地面流量, KZ表示Z方向上的饱和导水率, 下标LT表示该参数为稳态值。式(6)中计算的压力水头不能超过当地下水深度等于地面时的计算结果, 并受到稳态水力梯度的影响, 即:
| $ \psi (Z, t) \le Z\beta . $ | (7) |
TRIGRS模型采用较为简单的水量平衡方式计算地表径流产流机制, 假设运算时间域内土体达到饱和后无法入渗的降水将全部转化为地表径流, 流往运算区域下游网格。如下游网格内的降水量加上来自临近网格的地表径流量之和超过该网格的入渗量时, 该网格即产生地表径流, 流向下游临近网格。这一过程可由下式表示:
| $ I = P + {R_u}, \;\;\;\;I \le {K_s} $ | (8) |
| $ {R_d} = P + {R_u} - {K_s}, \;\;\;{R_d} \ge 0 $ | (9) |
式中: I为土壤入渗率; P为单位时间降水量; Ru为来自上游相邻网格的单位时间地表径流; Ks为饱和水力传导度; Rd为单位网格径流量。
5 模型输入参数TRIGRS模型运行时需要输入的参数较多, 且大多参数不易取得或无法适用于整个研究区域。根据陈则佑等(2011)、陈建新等(2011)和陈悦丽等(2016)的研究结果, 除进行实地数据采集外, 结合以往相关研究也可有效取得合理输入参数。将原始DEM完成洼地填充处理后, 计算研究区域坡度分布, 利用单流向D8算法提取水流方向栅格, 完成数据预处理工作。实验中选用结合流域水分交换与土壤水分模型TOPMODEL (Topography based Hydrological Model)地形指数的土壤厚度推算方程(雍斌等, 2007)计算研究区域土壤厚度, 该方程假设地形指数与土壤深度呈线性关系, 即:
| $ {D_j} = {C_S}\cdot{\rm{ln}}{(\alpha /{\rm{tan}}\beta)_j}, $ | (10) |
式中: Dj为j处的土壤厚度; ln(α/tanβ)j为j处的地形指数, 其中α为j处流域面积, β为坡度; CS为待定系数, 通过实地调查计算取得, 实验中取CS=0.357。计算结果如图 1(c)所示。其中河道地区土壤厚度最厚, 山顶地区较薄。
由于试验区域面积较大, 主要地质类型为碳酸盐岩与岩浆岩, 其中岩浆岩占全区域的60%以上。根据张廷山等(2006)中试验区域内地下水位高, 埋深浅, 地下水量一般较小的特点, 将稳态地下水深度根据不同分区取值, 范围为30~80 m。根据中国土壤数据库土壤类型分布及土壤含沙量将研究区域分为三个分区, 各分区土壤水力参数和抗剪强度参数根据《岩土工程实用手册》, 取值如表 1所示。
| 表 1 水力和抗剪强度参数取值 Table 1 Hydrological and shear strength parameters |
“7·23”特大暴雨过程前研究区域全境都出现零星降雨, 累积降雨量在100 mm以下, 土壤趋于饱和, 此时土壤初始入渗率小于或等于水力传导度一个次方以上, 因此假设初始渗透率I0为水力传导度的0.01倍, 而水力扩散度假设为水力传导度的100倍。模型中所输入降水数据基于研究区域内雨量站点泰森多边形[图 2(a)]的逐6 h面雨量分布, 以此检验模型对降水的响应能力。
6 模型运行结果采用空间分辨率30 m×30 m的数字高程资料进行TRIGRS模型分析, 模拟2010年“7·23”暴雨过程中研究区域受到雨水入渗后边坡稳定性的变化研究时段由2010年7月22日20:00开始, 至24日20:00结束, 计算每6 h时间间隔的累积降水, 通过雨量站泰森多边形计算面雨量栅格输入模型。研究结果以安全系数FS≤2为判定不稳定区域的条件, FS>2的区域视为稳定区域。
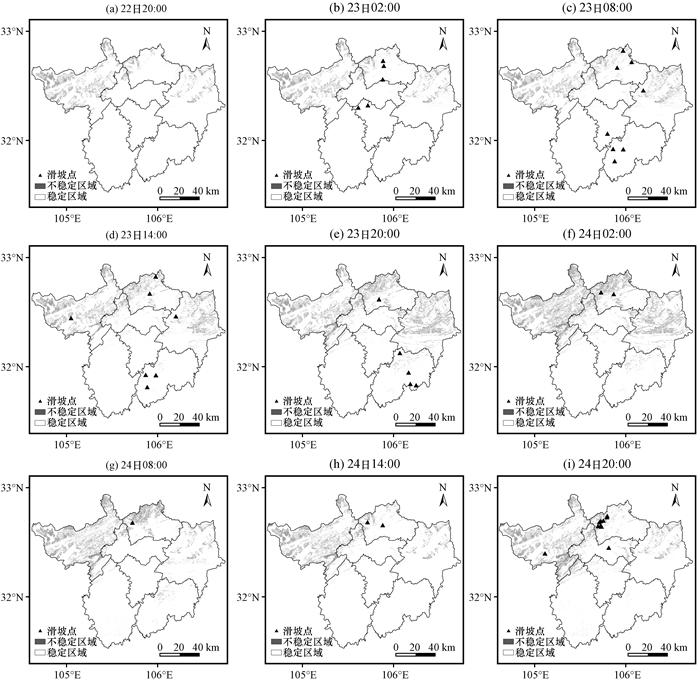
6.1 边坡安全系数对降水的响应从2010年7月22日20:00至25日02:00研究区6 h时间间隔TRIGRS模型模拟结果(图 4)中可见, 边坡安全系数的变化与累积降水量有明显相关性。22日20:00的模拟结果可见, 由于此前的零星降水, 边坡不稳定区域较为分散, 面积较小, 集中于研究区域东北部山高坡陡的旺苍县境内和西北部青川县境内。23日02:00降水中心位于研究区西部, 形成了一条自西南至东北的暴雨带, 中心降水量达到150 mm·(6h)-1, 为此次过程最大值。此时坡度较陡的研究区北部响应明显, 不稳定区域面积增加; 而研究区南部不稳定区域面积未出现明显变化。23日02:00-08:00降雨持续增大, 降水中心南移, 北部山区边坡不稳定区域由于雨水入渗量增大, 面积进一步扩大。14:00-20:00降水出现谷值, 累积降水量达到140 mm, 研究区全境边坡不稳定区域进一步扩大。24日02:00研究区东部出现新的暴雨中心, 中心降水量达到90 mm·(6h)-1。此时研究区东部边坡不稳定区域面积达到本次过程中的最大值, 坡度较缓的南部不稳定区域面积上升, 其中降水中心所在位置旺苍县南部和苍溪县境内不稳定区域增加明显, 全区不稳定面积升至3.3%, 这一结果显示当研究区累计降雨量达到140 mm左右时, 边坡稳定性开始产生较为明显的变化。24日08:00降水再次增大, 累积降水量超过150 mm, 降水中心分别位于东部和北部, 中心降水量为30~40 mm·(6h)-1, 降水面积减小。此时边坡稳定性模拟结果显示边坡不稳定区域范围减小, 东北部旺苍县境内减小尤为明显; 至24日14:00, 降水范围进一步缩小, 全区仅有一个最大降水量为50 mm·(6h)-1的降水中心, 位于研究区域西北部, 此时研究区域东部不稳定区域减小明显, FS < 1的栅格减少到1.52%。24日20:00研究区域开始新一轮降水过程, 降水较为分散, 面积较之前扩大, 范围集中在研究区域西部, 此时过程累积降雨量接近200 mm。此时的模拟结果显示全区域范围内FS < 1的栅格数再次增加, 上升至2.05%, 东北部和北部不稳定区域增加明显, 坡度较缓的南部区域也出现安全系数下降的区域, 与实际观测滑坡点基本吻合。
|
图 4 2010年7月22日20:00至24日20:00研究区6 h时间间隔TRIGRS模型模拟结果 Figure 4 Every 6 h trigrs model simulation results and landslide sites of study area from 20:00 on 22 to 20:00 on 24 July 2010 |
通过对比降水范围的变化及模拟结果发现, 部分区域边坡安全系数的变化相对降水存在6~12 h的滞后。以降水量最大的两个时段, 即2010年7月22日20:00至23日02:00及23日08:00-14:00为例, 两个时段的降水量分布[图 3(b), (c)], 可见研究区域全境均存在降水, 降水中心由广元市西北部逐渐转移至北部。而同一时段模型模拟结果[图 4(b), (c)]显示, 此时研究区域边坡不稳定范围未出现明显变化。本次降水峰值出现在2010年7月22日20:00至23日02:00时段, 而降雨中心相应位置边坡不稳定范围明显扩大发生在降水峰值出现约12 h后, 即23日14:00-20:00[图 4(d)]; 23日08:00-14:00时降雨中心位于研究区域西北部, 相应位置的边坡安全系数明显下降发生在12 h后的23日14:00-20:00这一时段[图 4(d)]。同时边坡安全系数的回升也存在6~12 h的滞后, 研究区域东北部除2010年7月22日20:00至23日02:00[图 3(b)]及23日08:00-14:00[图 3(c)]外, 只存在较为零星的降水, 而相应的边坡不稳定范围在23日14:00-20:00达到最大之后[图 4(d)], 在12 h后的24日08:00-14:00[图 4(g)]出现明显减小。根据模型计算原理, 这一滞后性与降水入渗过程有关, 区域坡度、土壤层厚度及土壤的水力参数均对入渗速率产生影响。坡度较大的区域的边坡稳定性受降雨影响较缓坡区域更为明显, 累积降水量达到100 mm左右时, 陡坡区域的边坡安全系数即出现明显变化, 而当累积降水量达到150 mm以上时, 坡度较缓的区域边坡稳定性出现下降, 且下降幅度较小, 显示坡度越缓越能承受高强度的降水, 这一结果与实际情况相符。
6.2 定量指数与ROC曲线定量指数QI(Quantitative Indices)由成功指数SI(Success Index)和错误指数EI(Error Index)组成, 针对整个流域的计算方法如下所示:
| $ S{I_n} = \frac{{\sum _{i = 1}^n\left({\frac{{{A_{{\rm{in}}, i}}}}{{{A_{{\rm{unst}}, i}}}}} \right)}}{n} \times 100, $ | (11) |
| $ E{I_m} = \frac{{\sum _{i = 1}^n\left({\frac{{{A_{{\rm{out}}, i}}}}{{{A_{{\rm{stab}}, i}}}}} \right)}}{n} \times 100, $ | (12) |
式中: Ain, i为整个流域模拟结果中的不稳定区域与实际发生滑坡区域的重合部分; Aunst, i为整个流域内实际发生滑坡的区域; Aout, i为整个流域模拟结果中的不稳定区域与实际发生滑坡区域的不重合部分; Astab, i为整个流域内未发生滑坡的区域。SIn和EIm分别为整个流域内成功指数和错误指数的累加, 可用于定量评估模型针对研究区域的预测能力。
实验中选用的滑坡点数据为四川省地质环境监测总站的滑坡观测记录, 2010年“7·23”暴雨过程中, 大部分滑坡发生在23日夜间至25日凌晨。因此选取降水开始60 h后, 即7月25日08:00的累积降水量作为降水输入参数, 安全系数FS < 2的模拟结果进行定量指数验证。将研究区域内高山地貌区和低山地貌区分开讨论, 定量指数计算结果如图 5(a)所示。
|
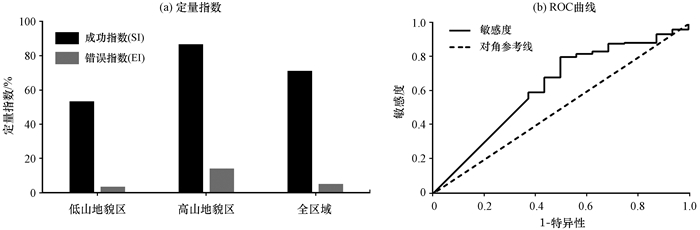
图 5 研究区域定量指数分析结果(a)及ROC曲线(b) Figure 5 The quantitative indices (a) and results of receiver operating characteristic (b) of study area |
定量指数计算结果显示模型高山地貌区模拟结果成功指数较高, 30个滑坡点中位于模拟结果不稳定区域中的有26个, 达到86.67%;同时错误指数也较高, 为14.07%。出现这一现象的原因与TRIGRS模型采用无限边坡稳定性分析计算斜坡稳定性有关, 高山地貌区地形更为接近无限边坡假设, 且高山地貌区坡度较大, 土壤抗剪强度较低, 在相同降雨情景下边坡稳定性下降速度更快; 且在“7·23”暴雨过程中, 高山地貌区累积降水量较大, 导致模拟结果边坡不稳定范围较大。低山地貌区模拟结果成功指数较低, 15个滑坡点中位于模拟结果不稳定区域中的仅有8个, 成功指数为53.33%, 错误指数较低, 为3.43%。低山地貌区因坡度较小, 土壤抗剪强度较高, 滑坡形态导致模拟结果中不稳定区域面积较小, 造成成功指数和错误指数都偏低。定量指数结果说明在无限边坡假设下, TRIGRS模型对于坡度较大的高山地貌区的边坡不稳定性模拟更好。全区域范围内模拟结果的成功指数为71.11%, 错误指数为5.08%, 说明TRIGRS模型对于试验区域本次暴雨过程的边坡稳定性有较好的预测能力。
受试者特征ROC(Receiver Operating Characteristics)曲线可以通过构建敏感度(True Positive Rate)和1-特异性(False Positive Rate)之间的关系检验模型分析的精度。ROC曲线中的曲线下面积AUC(Area Under Curve)的范围为0.5~1.0之间, 对应AUC更大的模型效果更好。基于降水开始60 h后的模拟结果, 在实验区域内随机选取200个单元, 位于滑坡区域内的记为正类, 反之记为负类, 将200个单元的安全系数值进行分析, 绘制ROC曲线[图 5(b)]。曲线下面积AUC=0.626, 具有统计学意义, 说明模型能够正确反映降水过程中研究区域的边坡稳定性变化。
7 结论与讨论(1) 选择四川省广元市作为实验区域, 应用基于栅格的瞬态降水入渗边坡稳定性模型TRIGRS模拟2010年“7·23”特大暴雨过程中边坡稳定性的变化。采用地形指数推估研究区域土壤厚度分布, 以逐6 h面雨量分布作为输入参数观察模拟结果对降水的响应。验证结果显示试验区域内模型模拟结果中, 边坡安全系数的下降与回升与实时降水变化存在6~12 h的滞后, 这一滞后时间随土壤类型、降水分布、坡度坡向等具体参数的变化而有所不同, 具体机制与较为精确的消退时间有待进一步实验验证。定量指数与ROC曲线计算结果显示模型对于试验区域“7·23”暴雨过程中的边坡稳定性变化有较好的预测能力, 能够正确反映降水过程中研究区域的边坡稳定性变化。
(2) 试验区域北部高山地貌区坡度较大, 边坡稳定性受降水影响较南部低山地貌区更大。当累积降水达到100 mm左右时, 高山地貌区的边坡安全系数出现大幅下降; 当累积降水达到140 mm左右时, 低山地貌区的边坡安全系数出现下降, 且幅度较小。在使用面雨量分布作为输入参数的前提下, 累积降水量与边坡不稳定范围并不呈正比关系, 未降水的区域边坡不稳定范围会随时间缩小。定量指数计算结果显示TRIGRS模型在边坡状态更符合无限边坡假设的研究区域北部高山地貌区预测效果更好, 达到80%以上; 在南部低山地貌区成功指数和错误指数均较低, 说明模型尚未能较好的反映低山地貌区的边坡稳定性受降水影响的变化情况, 这一不足可通过野外实地考察等方式进一步优化模型参数, 细化分区后加以改进。
(3) 调试后的TRIGRS模型对于降水的响应良好, 可用于研究区域内滑坡临界雨量计算与边坡不稳定性预测。目前广泛使用的滑坡预报方式为利用降雨强度-历时关系曲线(即I-D曲线, Intensity-Duration Curve)或人工神经网络等数学方法建立的经验模型, 只适用于小范围特定区域, 当下垫面条件发生变化时, 模型就不再适用。相对于原有滑坡预报方式所提供的确定性预报, 结合预测降水的TRIGRS模型提供的概率预报在时间和落区方面更加精细, 可以模拟降水过程中任意时间的边坡稳定性变化, 且在数据支持情况下, 模拟范围不受限制。当地形与地貌发生改变时, 只需修改输入参数, 原有模型适用性不受影响, 为相关部门滑坡预测业务的建设提供了新的思路。
(4) 模拟实验结果显示, 强降水为研究区域边坡稳定性变化的关键影响因子。通过目标区域的降水预报产品, 结合参数调试后的TRIGRS模型, 可以实现降水预报时段内目标区域的边坡稳定性预测。通过目前广泛应用的降水预报监测手段, 如数值天气预报模式、卫星降雨产品、雷达定量降水估测(QPE)和预报(QPF)系统及遥测雨量计等, 实现不同时间及空间尺度的灾害预报。实际业务中可使用中短期降水预报产品驱动TRIGRS模型判定危险区域, 进而通过短期临近降水预报产品实现定点灾害预报, 模型预测结果与降水产品同步循环更新。由于模型预测效果取决于降雨预报的准确性, 实际应用中需要尽量减少降水预报的不确定性。
本次实验中选取的滑坡记录数据来源为四川省地质环境监测总站的滑坡观测记录, 对滑坡发生时间与地点有详细记录, 但缺乏滑坡发生的具体范围与滑坡体积。如采用遥感图像分析配合实地勘探, 可对模型结果进行更为精确的验证。
Baum R L, Savage W Z, Godt J W, 2008. TRIGRS-A fortran program for transient rainfall infiltration and grid-based regional slope-stability analysis, version 2. 0[R]. U. S. Geological Survey Open-File Report, 2008-1159, 75.
|
|
Diana S, Jonathan W G, William Z, et al. 2006. Modeling regional initiation of rainfall-induced shallow landslides in the eastern umbria region of central italy[J]. Landslides, 3: 181–194.
DOI:10.1007/s10346-006-0037-0 |
|
Dongyeob K, Sangjun I, Sang H L, et al. 2010. Prediction the rainfall-triggered landslides in a forested mountain region using TRIGRS Model[J]. J Mountain Sci, 7: 83–91.
DOI:10.1007/s11629-010-1072-9 |
|
Eleonora G, Gabriella S, Maurizio F, et al, 2013. Rainfall induced shallow landslide forecasting in large areas: application of the trigrs model over a broad area of post-orogenic quaternary sediments[A]//Geological Society of America[C]//Denever, Colorado, USA: 125th Anniversary Annual Meeting & Expro. 27-30 October 2013.
|
|
Iverson R M. 2000. Landslide triggering by rain infiltration[J]. Water Res Res, 36(7): 1897–1910.
DOI:10.1029/2000WR900090 |
|
Park D W, Nikhili N V, Lee S R. 2013. Landslide and debris flow susceptibility zonation using TRIGRS for the 2011 seoul landslide event[J]. Natural Hazards and Earth System Science, 13: 2833–2849.
DOI:10.5194/nhess-13-2833-2013 |
|
Savage W Z, Godt J W, Baum R L, 2004, Modeling time-dependent areal slope stability[M]. Landslides: Evaluation and Stabilization/Glissement de Terrain: Evaluation et Stabilisation, 1: 23-36.
|
|
Savage W Z, Godt J W, Baum R L, 2003. A model for spatially and temporally distributed shallow landslide initiation by rainfall infiltration[M]. In Rickenmann D, Chen C, eds. Debris-flow hazards mitigation-mechanics, prediction and assessment: Rotterdam, Millpress, 179-187.
|
|
Srivastava R, Yeh T. 1991. Analytical solutions for one-dimensional, transient infiltration toward the water table in homogeneous and layered soils[J]. Water Res Res, 27: 753–762.
DOI:10.1029/90WR02772 |
|
陈建新, 谭志豪, 冀树勇, 等. 2011. 广域降雨促崩模式之建置及应用-以高屏溪流域为例[J]. 中华水土保持学报, 42(1): 1–11.
Chen J X, Tan Z H, Ji S Y, et al. 2011. An application of GIS-Based deterministic model for assessment of regional rainfall-induced landslide potential-example of Kao-Ping River Watershed[J]. J Chinese Soil Water Conservat, 42(1): 1–11.
|
|
陈悦丽, 陈德辉, 李泽椿, 等. 2016. 降雨型滑坡的集合预报模型及其初步应用试验研究[J]. 大气科学, 40(3): 515–527.
Chen Y L, Chen D H, Li Z C, et al. 2016. An ensemble prediction model for rainfall-induced landslides and its preliminary application[J]. Chinese J Atmos Sci, 40(3): 515–527.
|
|
陈则佑, 冯正一, 庄育蓁. 2011. 应用TRIGRS程式于边坡破坏机率分析-以奥万大地区为例[J]. 中华水土保持学报, 42(3): 228–239.
Chen Z Y, Feng Z Y, Zhuang Y C. 2011. An application of TRIGRS on slope failure probability analyses-a case study of Aowanda[J]. J Chinese Soil Water Conservation, 42(3): 228–239.
|
|
李兆平, 张弥. 2001. 考虑降雨入渗影响的非饱和土边坡瞬态安全系数研究[J]. 土木工程学报, 34(5): 57–61.
Li Z P, Zhang M. 2001. Effects of rain infiltration on transient safety of unsaturated soil slope[J]. China Civil Engineering Journal, 34(5): 57–61.
|
|
马振峰, 郭海燕, 詹兆渝, 等. 2016. 四川省气候综合图集[M]. 北京: 气象出版社.
Ma Z F, Guo H Y, Zhan Z Y, et al. 2016. Climate map synthesis of Sichuan Province[M]. Beijing: China Meteorological Press.
|
|
温克刚, 詹兆渝. 2006. 中国气象灾害大典四川卷[M]. 北京: 气象出版社.
Wen K G, Zhan Z Y. 2006. Meteorological hazards synthesis, Sichuan part[M]. Beijing: China Meteorological Press.
|
|
杨星, 王永前, 刘志红. 2016. 四川省2013年夏季卫星降雨数据的对比研究[J]. 高原气象, 35(4): 1039–1049.
Yang X, Wang Y Q, Liu Z H. 2016. Comparison of two different satellite precipitation data in Sichuan from May to August[J]. Plateau Meteor, 35(4): 1039–1049.
DOI:10.7522/j.issn.1000-0534.2015.00060 |
|
雍斌, 张万昌, 陈艳华. 2007. TOPMODEL中地形指数ln(α/tanβ)的新算法[J]. 地理研究, 26(1): 37–45.
Yong B, Zhang W C, Chen Y H. 2007. A new algorithm of the topographic index ln(α/tanβ) in TOPMODEL and its resultant analysis[J]. Geograp Res, 26(1): 37–45.
|
|
张廷山, 陈晓慧, 姜照勇, 等. 2006. 川东北红层区地下水赋存特征及合理开发思考[J]. 水资源与水工程学报, 17(1): 15–19.
Zhang T S, Chen X H, Jiang Z Y, et al. 2006. Characters and rational exploitation of underground water resources in red beds area of Northeast of Sichuan[J]. J Water Res Water Engineer, 17(1): 15–19.
|
|
张英平, 石建省, 甘建军, 等. 2011. 广元市次生地质灾害分布特征及影响因素分析-以朝天区为例[J]. 灾害学, 26(1): 75–79.
Zhang Y P, Shi J S, Gan J J, et al. 2011. Analysis of distribution characteristics and influencing factors of secondary geo-hazards in Guangyuan City[J]. J Catastrophology, 26(1): 75–79.
|
2. Heavy Rain and Drought-Flood Disasters in Plateau and Basin Key Laboratory of Sichuan Province, Chengdu 610072, Sichuan, China
 2018, Vol. 37
2018, Vol. 37
