2. 中国科学院大学, 北京 100049
Thornthwaite(1948)最早在气候分类的背景下提出潜在蒸发(Ep, potential evaporation, or potential evaporation capacity)概念, 指出气候对蒸发的制约, 气候条件可能的蒸发称为潜在蒸发。以后, 潜在蒸发的概念不断发展。Mahrt et al(1984)将潜在蒸发定义为独立于水面状态而由大气环境决定的自由水面的蒸发, Granger(1989)提出由大气状态和表面实际温度下的饱和蒸汽压来定义潜在蒸发, 代表潮湿表面的蒸发上限(Choudhury, 1997)。尽管这个概念最早作为气候指数发展起来, 但后来也被广泛应用在农学和水文学方面(Vörösmarty et al, 1998)。谢贤群等(2007)定义潜在蒸发为大气蒸发力的一个度量, 体现的是大气中控制充分供水下垫面蒸发速率的能力。Donohue et al(2010)测试了多种潜在蒸发计算方法捕捉蒸发力动态变化, 可用于准确描述气候变化对蒸发力的影响。Maeda et al(2011)用MODIS获取的地表温度数据代替气象站数据, 不仅将遥感和潜在蒸发结合起来, 更提高了估算精度。Wigmosta et al(1994)描述了分布式水文-植被模型, 包括冠层拦截、蒸发蒸腾、积雪融化以及通过饱和过剩机制产生的径流。研究蒸发原理对改善大气环流(Yates, 1997)、研究干旱区气候动态变化(钱正安等, 2017)以及维持灌区水资源供需平衡(吉喜斌等, 2005)至关重要。综上, 潜在蒸发既是陆地水分循环的重要环节(谢志鹏等, 2017), 也是能量平衡的关键部分(刘昌明等, 1999; 尹云鹤等, 2010), 研究潜在蒸发量的估算方法对于干旱半干旱区发展节水农业及提高作物产量等具有重要意义。
获取潜在蒸发量的方法主要有观测法和公式估算法, 观测法借助蒸发皿进行直接观测, 我国常规观测中使用Φ20型和E601型蒸发皿。Φ20型蒸发皿直径20 cm, 高10 cm, 周围有防护网以防止鸟类啄食, 安装在离地60 cm高的金属支架上, 可在不冻结情况下使用(张有芷, 1999)。E601型蒸发皿筒内径为61. 8 cm, 器口离地30 cm, 蒸发皿周围环有四个水圈, 水圈宽25 cm, 深18 cm, 冬季结冰时无法使用。国外通常使用Class A型蒸发皿, 直径120. 7 cm, 高25 cm, 安装在离地15 cm的标准木质底座上。尽管蒸发皿值与潜在蒸发量之间有差异, 但都能指示一定下垫面状态下大气的蒸发情况, 两者可用回归方程相联系(Zheng et al, 2009)。蒸发皿观测蒸发的实质是一定区域自由水面的最大可能蒸发量, 用来检测大气的蒸发力、指示大气干燥度, 并不代表实际蒸发量(任鹏程, 2013; 郭晨露等, 2017)。估算潜在蒸发量的公式约有50种(Lu et al, 2005), 按照所使用气象数据的不同可分为综合法、辐射法、温度法, 其中综合法包含的组合公式有Penman(1948)、FAO-56 Penman-Monteith(Allen et al, 1998), 基于辐射能量的计算公式有Priestley-Taylor(Priestley et al, 1972)、Makkink(Makkink, 1957)、Turc(Turc, 1961)和Doorenbos-Pruitt(Doorenbos et al, 1992), 基于温度原理的公式有Thornthwaite(Thornthwaite, 1948)、Hargreaves-Samani(Hargreaves et al, 1982)、Blaney-Criddle(Blaney, 1950)和Jensen-Haise(Jensen et al, 1963)。左德鹏等(2009)分析了石羊河流域基于温度的7种计算公式与FAO-56之间的拟合关系, 并建立起计算值与小型蒸发皿值之间的联系; Xu et al(2005)在三个不同气候地区对比分析了三种潜在蒸散发的补充公式在应用上的优缺点; Lang et al(2017)分析了8种计算公式与FAO-56之间的拟合关系, 发现基于辐射的计算公式在东南部适用性最好; Trajkovic et al(2009)借助湿润地区的数据分析了七种计算公式的适用性并发现Turc公式在该地区计算结果最为精确。尽管学者们在各公式的对比分析方面做了众多研究, 但是在干旱地区同时进行三类公式与蒸发皿观测值的分析比较较少, 且由于这些地区环境的限制使得布设各类仪器面临诸多困难, 因此有必要开展本文的研究, 为其他类似气候条件下在没有足够的气象数据或蒸发皿的情况下准确估算蒸发量提供支撑。
利用2015—2016年临泽站实测气象数据, 对比分析了10种日潜在蒸发量计算公式, 试图提出适用于干旱区潜在蒸发的计算方法, 并与用E601型和Φ20型蒸发皿观测得到的实际蒸发量进行比较, 建立起两者之间的关系, 为在没有条件布设蒸发皿的地区进行蒸发量的估算提供参考依据, 对潜在蒸发量的估算在农业规划和灌溉管理方面至关重要(Rahimikhoob et al, 2014)。同时计算了两种蒸发皿之间的折算系数及其与环境变量之间的统计关系, 利用主成分分析法总结出各气象因素对蒸发量的影响, 对于农业生态和水文学的发展意义重大(Roderick et al, 2007), 为陆面过程和水资源管理提供了关键参量。临泽内陆河流域研究站位于西北干旱区黑河流域中游绿洲农田交错带, 明确该地区的蒸发状况为合理制定灌溉制度和提高水资源利用率提供了参考依据。
2 资料与方法所使用气象资料来自中国科学院临泽内陆河流域研究站(39°19′ N, 100°08′ E; 海拔1 384 m)的气象观测站, 该站位于甘肃省张掖市临泽县平川镇, 地处西北干旱区, 年平均气温9. 2 ℃, 年均无霜期195天, 多年平均降水量在100 mm左右, 主要集中在7、8两个月, 属温带干旱气候。获取数据的观测仪器类型及时间步长等特性如下:温度和湿度采用HMP45D型温湿度传感器(Vaisala公司, 芬兰)数据, 观测高度2 m, 气温以小时为步长计, 日平均值按[(当日最低气温-前一日20:00气温)/2]+t8+t14+t20统计; 相对湿度日平均值按(2t8+t14+t20)/4统计; 气压采用DPA501型气压传感器测定, 仪器测量高度为70 cm, 以日为步长计; 净辐射采用QMN101型净辐射表获取, 测量高度为2 m, 以小时为时间步长; 风速数据采用WAA151型风速传感器(首立信科技有限公司, 中国)获得, 仪器的安装有2 m和10 m两种观测高度, 文中公式所需为2 m高处风速数据; 日照时数采用CSD1型日照仪(Kipp & Zonen公司, 芬兰)数据, 以分钟为观测步长, 在公式中应用时应换算为小时步长。考虑到影响蒸发的气象因素之间普遍存在相关关系, 若应用所有气象因素建立蒸发量影响因子模型则存在信息重叠, 且各气象要素之间不是一种简单的因果关系(左洪超等, 2005; 刘波等, 2006), 因此在研究气象要素对蒸发的影响时选用了主成分分析法, 即通过降维处理, 用较少的综合指标代替原来的变量指标, 解决信息重叠问题。
3 潜在蒸发计算方法按照不同类别分别选用公式:组合法选用Penman和FAO-56两种最常用的, 基于辐射能量的公式选用Priestley-Taylor、Makkink、Turc和Doorenbos-Pruitt四种, 基于温度的公式选用Thornthwaite、Hargreaves-Samani、Blaney-Criddle和Jensen-Haise四种, 其中各公式都是基于日时间步长的。
3.1 组合公式 3.1.1 Penman公式Penman于1948年首次提出潜在蒸散的概念, 并将空气动力学法和能量平衡法(热量平衡)结合起来用以计算潜在蒸散发量(Penman, 1948)。公式可拆分成由辐射平衡决定的热力项ΔRn/(Δ+γ)和由空气温度、风速和水汽压差决定的动力项γEa/(Δ+γ)。
| $ {E_p} = \frac{{\Delta ({R_n} - G) + \gamma {E_a}}}{{\Delta + \gamma }}, $ | (1) |
式中: Ep为潜在蒸发量(单位: mm·d-1); Δ=d(es)/dT为温度对饱和水汽压曲线的斜率(单位: kPa·℃-1); T为空气温度(单位: ℃); Ea=
| $ \gamma = \frac{{{c_p}P}}{{\lambda \varepsilon }} = 0.{\rm{ }}665 \times {10^{ - 3}}P, $ | (2) |
式中: cp为空气定压比热(单位: J·kg-1·℃-1); P为气压(单位: kPa); λ是蒸发潜热(单位: MJ·kg-1), 计算公式: λ=2. 501-(2.361×10-3)T; ε为水蒸气和干空气的相对分子量, 取值0. 622; Ea为空气干燥力(单位: mm·d-1); U2为高两米处的风速(单位: m·s-1)。
3.1.2 FAO-56 Penman-Monteith公式1998年联合国粮农组织(FAO)推荐的计算潜在蒸散量的标准公式是在综合考虑热量平衡、空气动力学阻抗和冠层表面阻抗的前提下, 一种适用于非饱和下垫面的潜在蒸散量计算公式。FAO定义参考作物蒸散量:参考植物高度为0. 12 m, 冠层阻抗为70 m·s-1, 反射率为0. 23, 近似于地表开阔, 水分充足, 高度一致, 生长旺盛且完全覆盖的草被冠层的蒸散量。70 m·s-1的冠层阻抗大约为一周灌溉一次的中度干燥的土壤表层的阻力(Allen et al, 1998)。该公式是统一标准的计算方法, FAO定义该法为计算蒸散发的首选方法。
| $ {E_p} = \frac{{0.{\rm{ }}408\Delta ({R_n} - G) + \gamma \frac{{900}}{{T + 273}}{U_2}({e_s} - {e_a})}}{{\Delta + \gamma (1 + 0.{\rm{ }}34{U_2})}}, $ | (3) |
以上为计算日平均蒸发量的参数, 若要计算每小时的潜在蒸发量, 需将900替换为37。式(3)中, U2=
该方法是一种基于能量平衡的简化的Penman公式, 忽略了空气动力学项而引入常数值, 相当于将空气动力学项的影响折算为辐射项的26%(借助海面和陆面资料得出的经验值)。
| $ {E_p} = {\alpha _{PT}}\frac{\Delta }{{\Delta + \gamma }}\frac{{\left({{R_n} - G} \right)}}{\lambda }, $ | (4) |
式中: αPT为Priestley-Taylor校准系数, 式中取值1. 26;其余参数同上。
3.2.2 Makkink公式Makkink(1957)估算了荷兰凉爽气候条件下草地的蒸散量, 该方法是在Penman公式的基础上用入射短波太阳辐射代替辐射平衡项进行简化, 并与蒸散仪观测数据对比校正得到的。公式为:
| $ {E_p} = {C_m}\frac{\Delta }{{\Delta + \gamma }}\frac{{{R_s}}}{\lambda } - 0.12, $ | (5) |
式中: Cm为修正系数, 一般取值0. 61; Rs=
该公式划分相对湿度区间, 在森林地区应用广泛(张士锋等, 2013), 被认为是最精确的估算湿润气候条件下的蒸散值的方法之一(Jensen et al, 1990)。
| $ {E_p} = \alpha \frac{{0.{\rm{ }}013}}{\lambda }\frac{{{T_a}}}{{{T_a} + 15}}(23.{\rm{ }}885{\rm{ }}6{R_s} + 50), $ | (6) |
式中:
该公式又被称为FAO-Radiation法, 常用于湿润地区草地蒸发量的估算(Doorenbos et al, 1992)。
| $ {E_p} = - 0.{\rm{ }}3 + {b_{dp}}\frac{\Delta }{{\Delta + \gamma }}{R_s} \times 0.{\rm{ }}408, $ | (7) |
式中: bdp=1.066-0. 001 3(RH)+0. 004 5(Ud)-0. 000 2(RH)(Ud)-0. 000 315(RH)2-0. 001 1(Ud)2; Ud为日间风速(单位: m·s-1); 其余参数同上。
3.3 基于温度的潜在蒸发计算公式 3.3.1 Thornthwaite公式Thornthwaite法是在美国中东部地区基于水量平衡提出的一种划分温度区间计算潜在蒸发量的方法。
| $ {E_p} = \left\{ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{T_a}<0℃\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;1.6C{\left({\frac{{10{T_a}}}{{{I^\alpha }}}} \right)^\alpha }, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0℃ \le {T_a} \le 26.5℃\\ C(- 415.85 + 32.24{T_a} - 0.43{({T_a})^2}), \;\;\;\;\;\;\;\;\;{T_a}>26.5℃ \end{array} \right. $ | (8) |
式中: α=67. 5×10-8I3-77. 1×10-6I2+0. 017 9I+0. 492;
该公式是在对美国加利福尼亚等干旱半干旱地区蒸散研究的基础上, 由Hargreaves et al(1982)提出典型的以温度与太阳辐射为基础的计算方法。
| $ {E_p} = 0.002\;3 \times 0.408 \times \left({T + 17.{\rm{ }}8} \right){({T_{{\rm{max}}}} - {T_{{\rm{min}}}})^{0.5}}{R_a}, $ | (9) |
式中: (Tmax-Tmin)为温度的变化幅度; 其余参数同上。
3.3.3 Blaney-Criddle公式FAO建议对于气象资料中只有温度的地区蒸发量的求算采用此法。
| $ {E_p} = {a_{BC}} + {b_{BC}}f, $ | (10) |
式中: f=p(0. 46T+8. 13), 为根据最低相对湿度日照小时和估计白天风力得出的修正系数; aBC=0. 004 3RHmin-(n/N)-1. 41; bBC=0. 82-0. 004 1(RHmin)+1. 07(n/N)+0. 066(Ud)-0. 006(RHmin)(n/N)-0. 000 6(RHmin)(Ud); p为实际日昼长小时数相对应于年昼长小时数的比例; RHmin为最小日相对湿度; 其余参数同上。
3.3.4 Jensen-Haise公式| $ {E_p} = {C_T}({T_{{\rm{mean}}}} - {T_x}) \times 0.408{R_s}, $ | (11) |
式中: CT=0. 025; Tx=3;其余参数同上。
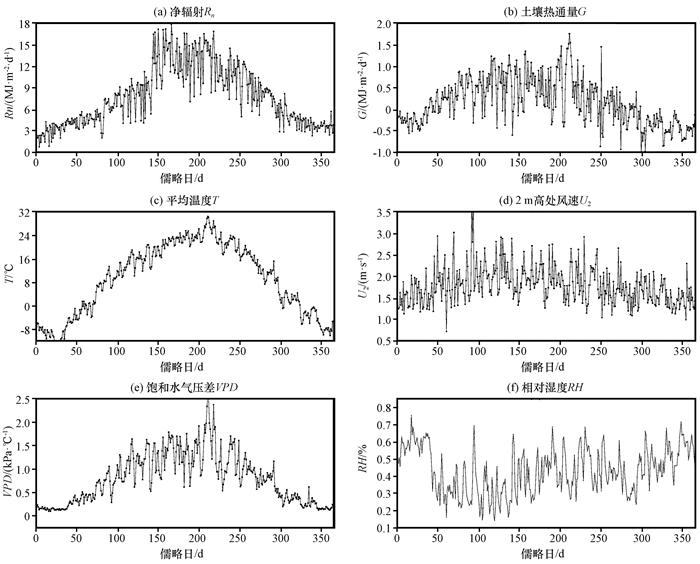
4 结果 4.1 主要气象要素季节变化特征蒸发皿蒸发量的变化是周围环境要素共同作用的结果, 明确各要素的变化特征将会为分析蒸发量的时间变化提供理论依据。图 1、2分别以日、月为时间步长展示了影响蒸发的6种气象要素的变化特征, 即净辐射Rn、土壤热通量G、平均温度T、2 m高处风速U2、饱和水气压差VPD和相对湿度RH。从图 1可以看出, Rn、T和VPD的日变化呈现明显的先增后减趋势, 均在第200天前后达到峰值, 可以初步判定三者在变化特征上存在某种相关关系。G值在0~1 MJ·m-2·d-1之间波动, 取值非常小, 可以看到其变化也表现出先增后减的趋势。U2峰值出现在第100天前后, 春季变化较大, 高达2 m·s-1, 其他季节变化较小, 在1. 5 m·s-1上下波动。RH与气温息息相关, 在第50天前后开始呈下降趋势, 但这段时间内温度始终呈上升势, 这是因为气温升高时, 蒸发作用加强, 水气压虽增大但饱和水气压增大更多, 空气中所能容纳的水汽含量增加, 因此相对湿度反而降低; 在第150~300天之间, RH先增后减, 该时段内相对湿度可能受降水量影响较多; 而第300天之后RH又有所增加, 此时气温降低, 空气中能容纳的水汽减少, 因此RH反而增大。
|
图 1 各气象要素逐日变化特征 Figure 1 Daily variation characteristics of meteorological elements |
|
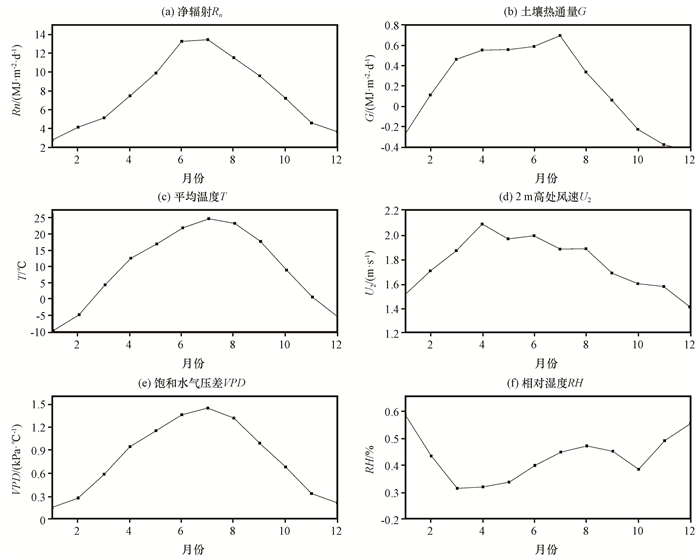
图 2 各气象要素月均变化特征 Figure 2 Monthly variation characteristics of meteorological elements |
Rn、T和VPD的月变化(图 2)均在7月达到峰值, 且变化趋势相同; 从图 2(d)来看, G也在7月达到峰值, 且过后呈直线下降; U2在春季4月时取得最大值, 在冬季12月取得最小值, 变化幅度较小; RH在春季升温月份有明显的下降趋势, 而在秋冬降温时节又出现了增加的势头。
4.2 蒸发皿数据季节变化趋势及驱动因素分析以日、月时间步长展示两种蒸发皿数据Epan(单位: mm·d-1)的变化特征, 其中冬季月份(1, 2, 3, 11和12月)两种蒸发皿均无观测数据。
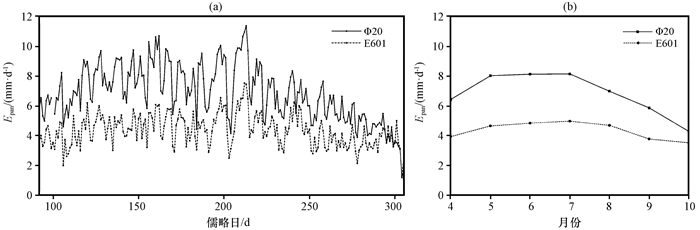
结合两种蒸发皿蒸发量逐日及月均变化特征(图 3)及蒸发量的最大值及折算系数(表 1)可知, Φ20型蒸发皿数据明显高于E601型, 4—10月总值高出539. 90 mm·d-1。两种蒸发皿测得的蒸发量都在夏季月份达到峰值, 从图 3(b)月均变化特征来看, Φ20型蒸发皿值达到峰值的时间要稍早于E601型, Φ20型蒸发皿最大值出现在7月, 为11. 38 mm·d-1, 月均最大值出现在6月, 为8. 13mm·d-1, E601型蒸发皿最大值出现在7月, 为7. 53 mm·d-1, 月均最大值也出现在6月, 为4. 84 mm·d-1, 虽然两种蒸发皿数据有所偏差, 但在相同气象因素的驱动下, 蒸发皿的年内变化趋势基本一致, 这就为计算两种蒸发皿折算系数提供了条件。
|
图 3 两种蒸发皿蒸发量Epan逐日(a)及月均(b)变化特征 Figure 3 Daily (a) and monthly (b) variation characteristics of two kinds of evaporation pan (Epan) data |
| 表 1 两种蒸发皿蒸发量月均值、最大值及折算系数 Table 1 Monthly average values, maximum values and conversion coefficients of two evaporation pan data |
按照算术平均法计算E601型蒸发皿与Φ20型蒸发皿的折算系数(表 1), 变化特征如下: 4—10月折算系数均值为0. 65, 各月系数具有一定的变化; 折算系数10月最大, 为0. 86, 5月最小, 为0. 58, 最大值与最小值相差0. 28。建立蒸发皿折算系数与净辐射之间的相关关系来进一步分析影响蒸发皿系数的环境要素(图 4), 发现相关系数为-0. 33(P<0. 01), 说明两者之间存在极显著的负相关关系。
|
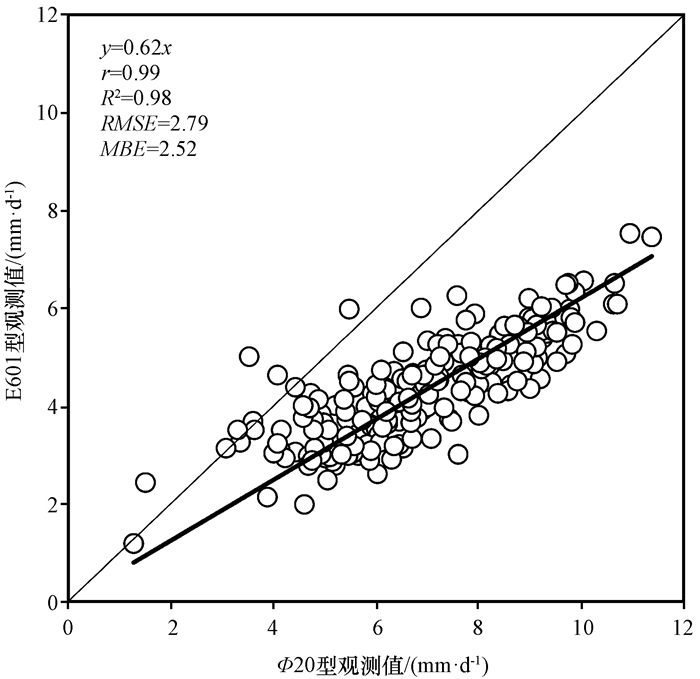
图 4 两种蒸发皿蒸发量之间的相关性 Figure 4 Correlation between two evaporation pan data |
对两种蒸发皿值做截距取为零的一元线性回归并进行相关性检验(夏依木拉提·艾依达尔艾力等, 2011), 相关系数为0. 99(P<. 01), 相关性极高且通过了0. 01水平显著性检验, 斜率为0. 62, 即该方法计算的蒸发皿折算系数为0. 62, 比用算术平均法计算的值小0. 03。从数理统计原理来看, 一元线性回归方程的估算值能消除观测差异造成的误差, 结果更加合理。
对Rn、T、U2、VPD和RH五种气象因素做主成分分析, 根据主成分对应特征值大于1的原则, 提取了前两个主成分, 累计方差贡献率达76%, 表明前两个主成分能够代表最初的五个影响蒸发的气象因素, 各主成分的载荷值见表 2。
| 表 2 主成分分析结果 Table 2 The results of principal component analysis |
第一主成分方差贡献率为51%, 其主要在Rn、T、VPD三个因素上占比较大, 空气具有热胀冷缩性, 当辐射增加温度升高时, 空气膨胀, 气压降低, 反之, 气压增大, 可知大气辐射、热量特征和气压可共同作用于蒸发, 且三者对蒸发量的增加都起到促进作用。第二主成分方差贡献率为25%, 主要在U2、RH上占比较大, 故认为其代表了空气动力和湿度特征, 其中风速占比-59%, 说明在第二主成分的因素上, 风速对蒸发量的增加起到抑制作用, 相对湿度占比84%, 说明其对蒸发量的增加起促进作用。
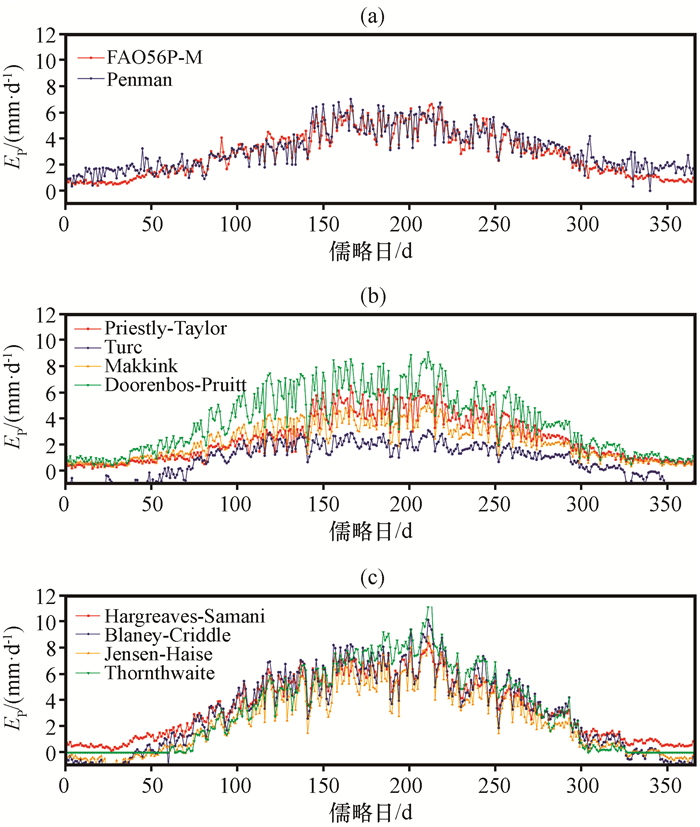
4.3 不同潜在蒸发估算方法计算结果对比图 5为多种公式计算2015—2016年日潜在蒸发量Ep。从图 5中可以看出, 年内变化总体呈现先增后减趋势, 与Rn、T和VPD的年内变化趋势相同。两种综合法计算的蒸发量[图 5(a)]在全年都拟合度极高, 冬季Penman法计算的日潜在蒸发量值比FAO-56法稍大, FAO-56法最大值出现在7月(6. 62 mm·d-1), Penman法最大值出现在6月(7. 00 mm·d-1), 仅相差0. 38 mm·d-1, 两种方法均考虑了辐射项和空气动力项, 校准参数的不同造成了潜在蒸发值的差异。基于辐射能量的各方法计算值[图 5(b)]差异较大, Doorenbos-Pruitt法计算值高于其他三种, 夏季尤为明显, 且年内变化差异较大, 最大值出现在7月(8. 83 mm·d-1); 从图中可以看出Priestly-Taylor法与Makkink法计算值差异不大, 年总值为898. 61 mm·d-1, 而Makkink法年总值为806. 00 mm·d-1; Turc法在冬季月份计算值为负, 年总值仅为388. 07 mm·d-1, 明显小于其他各方法计算值, 所以在该地区使用此公式时应对其系数进行校正。基于温度的各公式[图 5(c)]计算值在夏秋季节曲线走势相似度较高, 最大值均出现在7月, 仅在冬季差异明显, 各方法计算值最大的是Hargreaves-Samani法, 年总值为1 242. 54 mm·d-1; Thornthwaite法计算值年内差异较大, 日最大值为11. 40 mm·d-1, 年总值也较大, 为1 210. 12 mm·d-1; 而年总值最小的是Jensen-Haise法, 仅为902. 49 mm·d-1, Blaney-Criddle法计算值年内差异也较大, 最大值达10. 10 mm·d-1。
|
图 5 不同潜在蒸发计算公式日变化 Figure 5 Daily change of different potential evaporation methods |
以两种蒸发皿蒸发量分别作为自变量, 不同方法计算Ep值为因变量, 用回归方程对二者进行拟合, 以决定系数R2来表示回归方程拟合的好坏。为验证各潜在蒸发计算方法估算蒸发量的精度, 计算了蒸发皿日蒸发量与各计算日值之间的均方根误差(RMSE)、平均偏差(MBE), 二者绝对值越小, 表明两种方法之间的差异越小。
| 表 3 不同潜在蒸发计算公式月平均值及最大值 Table 3 Monthly average values and maximum values of different potential evaporation methods |
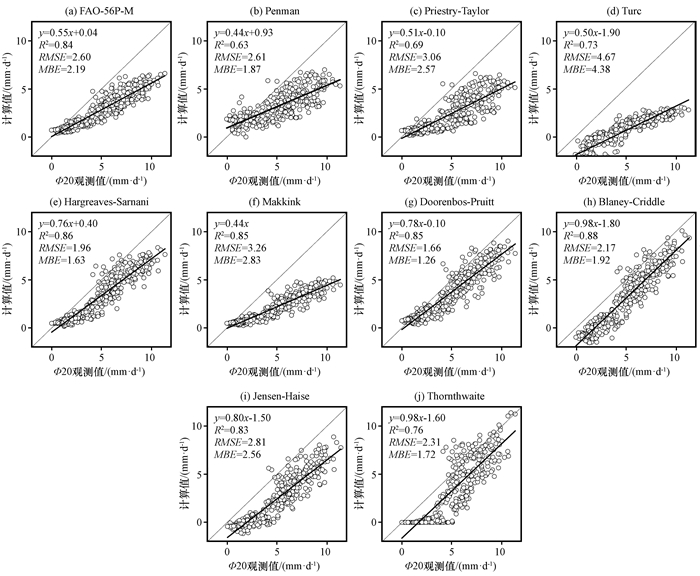
不同计算公式与Φ20型蒸发皿的拟合程度差别不大(图 6), 难以区分出各公式的代表性强弱。与Φ20型蒸发皿测得的蒸发量建立的回归方程中拟合程度最好的是Blaney-Criddle法, 斜率为0. 98, R2为0. 88, 比拟合度最差的Penman公式(R2=0. 63)高了0. 25, 但该公式所求值在全年都低估了蒸发皿值; Hargreaves-Samani法、Makkink法、Doorenbos-Pruitt法、FAO-56法和Jensen-Haise法的R2都在0. 80之上, 说明这几种方法计算值与E601型蒸发皿值回归方程的拟合度均较好, 但它们都对蒸发皿值有不同程度的低估现象。与Φ20型蒸发皿值相比较, RMSE最小的是Doorenbos-Pruitt法和Hargreaves-Samani法, 分别为1. 66和1. 96 mm·d-1, 同时这两种方法的MBE也较小, 分别为1. 26和1. 63 mm·d-1; 其次为Thornthwaite法、Blaney-Criddle法, 其RMSE分别为2. 31和2. 17 mm·d-1, 同时考虑与蒸发皿值建立回归方程拟合程度的好坏可知, Blaney-Criddle法、Doorenbos-Pruitt法和Hargreaves-Samani法应用在该地区以代替Φ20型蒸发皿值效果较好。RMSE和MBE最大的都是Turc公式, 可见此公式在该地区对蒸发皿蒸发量不具典型代表性。与Φ20型蒸发皿值相比较, 所选用的各个公式都不同程度地低估了蒸发皿值。
|
图 6 不同方法计算Ep值与Φ20型蒸发皿蒸发量的线性关系 Figure 6 Linear relationship between calculated Ep values of different methods and evaporation pan data of Φ20 |
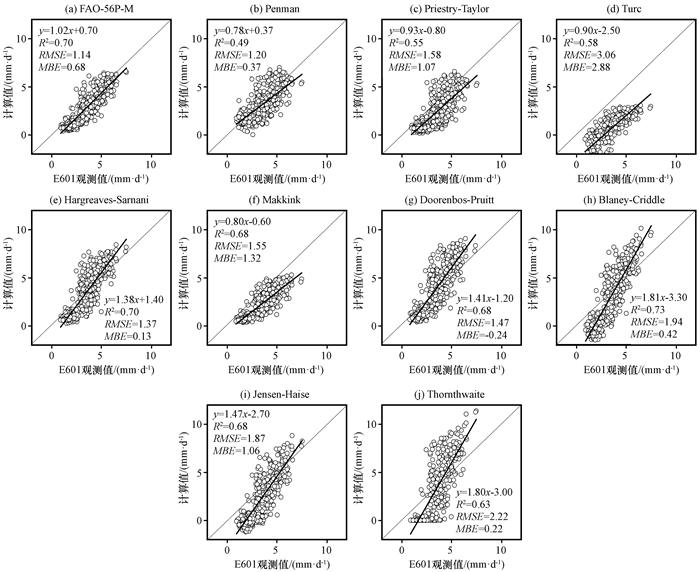
与E601型蒸发皿值建立的回归方程拟合程度最好的是Blaney-Criddle法计算值(图 7), R2为0. 73, 但该公式在蒸发量较小时容易低估蒸发皿值, 而在蒸发量较大时又高估了蒸发皿值; 其次是FAO-56法和Hargreaves-Samani法, R2都为0. 70, 斜率分别为1. 02和1. 38, 斜率接近于1且相关系数较高, 说明FAO-56P-M法和Hargreaves-Samani法计算值与E601型蒸发皿测得的蒸发量拟合度最好且差别较小, 但Hargreaves-Samani法与Blaney-Criddle法存在同样的问题, 在蒸发量较小时低估了蒸发皿值, 在蒸发量较大时又高估了蒸发皿值; 回归方程拟合度最差的是Penman法, R2仅为0. 49, 但从与E601型蒸发皿的RMSE和MBE来看, 该法所求值分别为1. 20和0. 37 mm·d-1, 且该公式计算值均匀地分布在1:1线上下, 与蒸发皿值的差异较小, 在该地区使用时效果也较好; RMSE最小的是FAO-56公式, 仅为1. 14 mm·d-1, 且其MBE也较小, 其次为Hargreaves-Samani法和Doorenbos-Pruitt法, RMSE分别为1. 37和1. 47 mm·d-1, 同时其MBE最小, 分别为0. 13和-0. 24 mm·d-1。从所分的三类公式来看, 综合法对蒸发皿值的估算较为准确, 基于辐射的各计算方法容易低估蒸发皿值, 而基于温度的各计算公式在蒸发量较小时会低估蒸发皿值, 在蒸发量较大时又容易高估蒸发皿值。综上所述, 用来代替E601型蒸发皿值效果最好的是FAO-56和Hargreaves-Samani法的计算值。
|
图 7 不同方法计算Ep值与E601型蒸发皿蒸发量的线性关系 Figure 7 Linear relationship between calculated Ep values of different methods and evaporation pan data of E601 |
通过比较各计算值与两种蒸发皿值的关系, 得到有蒸发皿观测值的4—10月份的蒸发皿系数, 通过蒸发皿系数建立起二者之间的经验关系, 从而为利用蒸发皿值简单而准确地估算Ep提供了参考依据。
按照Allen et al(1998)的研究, 在不同情况下的蒸发皿系数值在0. 35~0. 85之间, 对比表 4和表 5中的蒸发皿系数可知, Φ20型蒸发皿系数中, Turc法值偏小, 仅为0. 25, 而其他各法计算的蒸发皿系数均在合理范围内; E601型蒸发皿系数中, 仅Priestly-Taylor法、Turc法、Makkink法计算的蒸发皿系数在合理范围之内, 其余各法计算值都偏大。
| 表 4 不同方法计算Ep值与Φ20型的蒸发皿系数 Table 4 Pan evaporation coefficient between calculated Ep values of different methods and evaporation pan data of Φ20 |
| 表 5 不同方法计算Ep值与E601型的蒸发皿系数 Table 5 Pan evaporation coefficient between calculated Ep values of different methods and evaporation pan data of E601 |
选取对蒸发皿值影响较大的三个环境因素, Rn、T和VPD, 分别计算其4—10月值与各蒸发皿系数的相关系数(表 6)。由表 6可知, Penman法计算值与Φ20型蒸发皿的蒸发皿系数和T建立的相关系数-0. 13、与E601型蒸发皿的蒸发皿系数和VPD建立的相关系数-0. 05以及Priestly-Taylor法计算值与Φ20型蒸发皿的蒸发皿系数和VPD建立的相关系数0. 09均未通过0. 01水平上的极显著性检验, Hargreaves-Samani法计算值与E601型蒸发皿的蒸发皿系数和VPD建立的相关系数0. 37仅通过0. 05水平的显著性检验, 除此之外, 其余各相关系数均达到了极显著水平, 说明蒸发皿系数与这三种环境要素之间确实存在某种关联, 利用环境要素来计算蒸发皿系数的公式有多种(Snyder, 1993), 在气候条件不同的地区, 各环境要素对蒸发皿系数的影响是有差异的, 因此应根据当地的气候选取合适的计算公式或对原式进行校正后使用。
| 表 6 蒸发皿系数与气象要素的相关系数 Table 6 Correlation coefficients between evaporation pan coefficients and meteorological elements |
蒸发皿的材质、大小、安装高度以及其内水分接触风、气压状态的不同会影响蒸发量, 因此水分蒸发速率是周围环境因子共同作用的结果(陈伯龙等, 2017), 同时蒸发皿侧壁也会受到太阳辐射和地表反射辐射的作用, 其蒸发过程远比水面蒸发复杂(陈伯龙等, 2014)。E601型蒸发皿周围的防外溅装置, 可防止在降雨日将外溅的水算作蒸发量(王梅等, 2004), 提高了测量精度; 装置布设在土壤中, 容水多, 与实际水面蒸发更为接近, 而Φ20型水量少, 安装高度较高, 风速大, 可加速蒸发进行, 因此Φ20型蒸发皿值明显高于E601型。主成分分析法分析各环境要素与蒸发皿值的关系显示, Rn、T和VPD三个因素对蒸发皿值的变化影响较大。公式计算值比蒸发皿蒸发量最大值出现的月份滞后, 原因在于各计算公式仅考虑了辐射和温度的影响, 忽略了空气动力学项, 而蒸发皿蒸发还受到气压、风速和相对湿度等因素的综合影响。
各计算值偏差较大主要由于采用了不同的校正系数, 得到了不同的空气动力学项和辐射项。各公式的由来都基于特定的地区和气候背景, 参数也是依靠经验计算所得(高冠龙等, 2017), 在其他地区使用时需加以修正, 否则结果会有所偏差。
Doorenbos-Pruitt法、Hargreaves-Samani法、FAO- 56法、Hargreaves-Samani法适用于计算该地区潜在蒸发, 其计算值与蒸发皿值之间回归方程的拟合程度较好且偏差较小。FAO-56法与两种蒸发皿值拟合关系均较好, 该公式综合考虑了空气动力学因素和辐射情况, 经多方验证, 式中系数在各地区使用时无需进行校正, 而同样作为综合法使用的Penman法计算值与两种蒸发皿值的拟合程度却均较差。Blaney-Criddle法和Hargreaves-Samani法都是基于干旱地区提出的, 适用性较强, Hargreaves-Samani法只涉及最高温与最低温, 因此在气象资料不全时也能取得较满意的结果, 被广泛应用在辐射数据缺乏的地区。Blaney-Criddle法计算值虽拟合程度最好, 但在冬季有负值出现, 排除误差因素的影响, 可能与公式本身原理有关, 该公式在有风、干燥且晴朗的地区, 会低估蒸发量, 在无风、湿润且多云的地区, 又容易高估蒸发量(Sasireka et al, 2017)。Makkink法与两种蒸发皿值的拟合程度均较好, 该法以太阳短波辐射代替辐射平衡项对Penman法进行简化, 太阳辐射作为地表能量的最终来源, 对其准确估算是求算蒸发量的重要环节, 本文在计算时采用祝昌汉(1982)研究中的校准系数, 刘昌明等(2011)在计算中国水资源10大流域片区潜在蒸散发时引入了邱新法等(2008)的太阳辐射优化模型, 根据地区气候校正系数, 优化后的太阳辐射误差减小了50%, 提高了计算精度。Priestly-Taylor法在该地区使用时选用原式中的系数1. 26, 效果较差, Xu et al(2002)研究表明在干旱区使用时需将校准系数乘上经验常数, Priestly et al (2009)将αPT取为1. 74, 求得年总值为1 242. 90 mm·d-1, 与Hargreaves-Samani法计算值十分接近; 若以FAO-56或Penman公式作为该地区计算潜在蒸发量的标准公式, 则αPT应分别取为1. 46和1. 62, 若以该地区与蒸发皿值拟合效果最好的Blaney-Criddle公式作为计算潜在蒸发量的标准公式, 则αPT应取为1. 60, 可知在该地区参数取在1. 46~1. 74间应用效果较好。
以下公式用于计算该地区潜在蒸发时不具优越性。Thornthwaite公式在有足够水分用于蒸发的山谷地区最为适用, 但由于它仅需要月均温一个参数, 因此常被误用在蒸发条件不充分的干旱半干旱地区(Xu et al, 2001)。Jensen-Haise法计算值偏低, 该公式是借助土壤取样数据评估了大量蒸散发观测值之后, 得到的经验公式, 常用于湿润半湿润区草地蒸散发估算(Jensen et al, 1963), 同样被应用在湿润气候条件下的还有Turc法, 该法最早被应用在欧洲西部一般气候条件下计算以10天为一个周期的潜在蒸散量, 湿润地区在温度低时相对湿度较大, 而干旱区在温度较低的月份相对湿度也较低, 计算结果会有负值出现, 因此在干旱半干旱区使用时会产生较大的误差。
6 结论采用10种方法计算了临泽站2015—2016年日潜在蒸发量, 并与两种类型蒸发皿观测值进行对比, 得到以下主要结论:
(1) 影响蒸发皿蒸发量的环境因素从高到低依次为饱和水气压差、净辐射、温度。
(2) 按照算术平均法计算E601型蒸发皿与Φ20型蒸发皿的折算系数均值为0. 65, 且具有季节变化, 主要与太阳辐射有关。
(3) 适合于计算该地区潜在蒸发量的公式有FAO-56法、Doorenbos-Pruitt法、Blaney-Criddle法和Hargreaves-Samani法。
(4) Doorenbos-Pruitt法、Hargreaves-Samani法计算值与Φ20型蒸发皿值建立的蒸发皿系数分别为0. 77和0. 71, FAO-56和Hargreaves-Samani法计算值与E601型蒸发皿值建立的蒸发皿系数分别为0. 91和1. 12。
以上研究结果为在气象数据不足的具有类似气候条件的地区准确估算蒸发量提供了支撑, 也为没有条件布设蒸发皿的地区用公式计算潜在蒸发量来代替蒸发皿值提供了方法上的选择。
Allen R G, Pereira L S, Raes D, et al. 1998. Crop evapotranspiration:Guidelines for computing crop water requirements. Irrigation and Drainage Paper No 56[M]. Rome, Italy Allen: Food and Agriculture Organization of the United Nations (FAO).
|
|
Blaney H F, Criddle W D. 1950. Determining water requirements in irrigated areas from climatological and irrigation data[J]. US Department of Agriculture, Soil Conservation Service, 48.
|
|
Choudhury B J. 1997. Global pattern of potential evaporation calculated from the Penman-Monteith equation using satellite and assimilated data[J]. Remote Sens Environ, 61(1): 64–81.
DOI:10.1016/S0034-4257(96)00241-6 |
|
Donohue R J, Mcvicar T R, Roderick M L. 2010. Assessing the ability of potential evaporation formulations to capture the dynamics in evaporative demand within a changing climate[J]. J Hydrol, 386(1/4): 186–197.
|
|
Doorenbos J. 1992. Crop water requirements[J]. FAO Irrigation & Drainage Paper Rome, 24: 322–334.
|
|
Granger R J. 1989. An examination of the concept of potential evaporation[J]. J Hydrol, 111(1/4): 9–19.
|
|
Hargreaves G H, Samani Z A. 1982. Estimating potential evapotranspiration[J]. Journal of the Irrigation & Drainage Division, 108(3): 225–230.
|
|
Jensen M E, Haise H R. 1963. Estimating evapotranspiration from solar radiation[J]. Proceedings of the American Society of Civil Engineers, Journal of the Irrigation and Drainage Division, 89: 15–41.
|
|
Jensen M E, Burman R D, Allen R G. 1990. Evapotranspiration and irrigation water requirements:ASCE-Manuals and reports on engineering practice No. 70[M]. New York: The American Society.
|
|
Lang D, Zheng J, Shi J, et al. 2017. A comparative study of potential evapotranspiration estimation by eight methods with FAO Penman-Monteith Method in southwestern China[J]. Water, 9(10): 734.
DOI:10.3390/w9100734 |
|
Lu J, Sun G, Mcnulty S G, et al. 2005. A comparison of six potential evapotranspiration methods for regional use in the southeastern United States[J]. Journal of the American Water Resources Association, 41(3): 621–633.
DOI:10.1111/jawr.2005.41.issue-3 |
|
Maeda E E, Wiberg D A, Pellikka P K E. 2011. Estimating reference evapotranspiration using remote sensing and empirical models in a region with limited ground data availability in Kenya[J]. Appl Geography, 31(1): 251–258.
DOI:10.1016/j.apgeog.2010.05.011 |
|
Mahrt L, Ek M. 1984. The influence of atmospheric stability on potential evaporation[J]. J Appl Meteor, 23(2): 222–234.
DOI:10.1175/1520-0450(1984)023<0222:TIOASO>2.0.CO;2 |
|
Makkink G F. 1957. Testing the Penman Formula by means of lysimeters[J]. J Inst Water Engineers, 11(3): 277–288.
|
|
Penman H L. 1948. Natural evaporation from open water, hare soil and grass[J]. Proc Roy Soc London, 193(1032): 120–145.
DOI:10.1098/rspa.1948.0037 |
|
Priestley C H B, Taylor R J. 1972. On the assessment of surface heat flux and evaporation using large-scale parameters[J]. Mon Wea Rev, 100(2): 81–92.
DOI:10.1175/1520-0493(1972)100<0081:OTAOSH>2.3.CO;2 |
|
Rahimikhoob A, Hosseinzadeh M. 2014. Assessment of Blaney-Criddle equation for calculating reference evapotranspiration with NOAA/AVHRR data[J]. Water Resources Management, 28(10): 3365–3375.
DOI:10.1007/s11269-014-0670-7 |
|
Roderick M L, Rotstayn L D, Farquhar G D, et al. 2007. On the attribution of changing pan evaporation[J]. Geophys Res Lett, 34(34): 251–270.
|
|
Sasireka K, Reddy C J M, Reddy C C, et al, 2017. Evaluation and recalibration of empirical constant for estimation of reference crop evapotranspiration against the modified Penman Method[C]//IOP Conference Series: Earth and Environmental Science. IOP Publishing.
|
|
Snyder R L. 1993. Equation for evaporation pan to evapotranspiration conversions[J]. Journal of Irrigation & Drainage Engineering, 118(6): 977–980.
|
|
Thornthwaite C W. 1948. An approach toward a rational classification of climate[J]. Geograp Rev, 38(1): 55–94.
DOI:10.2307/210739 |
|
Trajkovic S, Kolakovic S. 2009. Evaluation of reference evapotranspiration equations under humid conditions[J]. Water Resources Management, 23(14): 3057–3067.
DOI:10.1007/s11269-009-9423-4 |
|
Turc L. 1961. Evaluation de besoins en eau d'irrigation, évapotranspi-ration potentielle[J]. Ann Agron, 12(1): 13–49.
|
|
Vörösmarty C J, Federer C A, Schloss A L. 1998. Potential evaporation functions compared on US watersheds:Possible implications for global-scale water balance and terrestrial ecosystem modeling[J]. J Hydrol, 207(3/4): 147–169.
|
|
Wigmosta M S, Vail L W, Lettenmaier D P. 1994. A distributed hydrology-vegetation model for complex terrain[J]. Water Resour Res, 30(6): 1665–1679.
DOI:10.1029/94WR00436 |
|
Xu C Y, Singh V P. 2001. Evaluation and generalization of temperature-based methods for calculating evaporation[J]. Hydrological Processes, 15(2): 305–319.
DOI:10.1002/(ISSN)1099-1085 |
|
Xu C Y, Singh V P. 2002. Cross comparison of empirical equations for calculating potential evapotranspiration with data from Switzerland[J]. Water Resources Management, 16(3): 197–219.
DOI:10.1023/A:1020282515975 |
|
Xu C Y, Singh V P. 2005. Evaluation of three complementary relationship evapotranspiration models by water balance approach to estimate actual regional evapotranspiration in different climatic regions[J]. J Hydrol, 308(1): 105–121.
|
|
Yates D N. 1997. Approaches to continental scale runoff for integrated assessment models[J]. J Hydrol, 201(1): 289–310.
|
|
Zheng H, Liu X, Liu C, et al. 2009. Assessing contributions to pan evaporation trends in Haihe River Basin, China[J]. J Geophys Res, 114(D24): 144–153.
|
|
陈伯龙, 左洪超, 高晓清. 2014. 干旱区气象因子对蒸发皿蒸发量的影响[J]. 高原气象, 33(5): 1251–1261.
Chen B L, Zuo H C, Gao X Q. 2014. Effect of meteorological factors on pan evaporation in arid region[J]. Plateau Meteor, 33(5): 1251–1261.
DOI:10.7522/j.issn.1000-0534.2013.00060 |
|
陈伯龙, 左洪超, 高晓清, 等. 2017. 蒸发皿蒸发及能量变化过程的微气象观测研究[J]. 高原气象, 36(1): 87–97.
Chen B L, Zuo H C, Gao X Q, et al. 2017. Study on pan evaporation and energy change process by micro-meteorological method[J]. Plateau Meteor, 36(1): 87–97.
DOI:10.7522/j.issn.1000-0534.2016.00021 |
|
高冠龙, 冯起, 张小由, 等. 2017. 蒸散发模型结合微气象数据模拟陆面蒸散发研究进展[J]. 高原气象, 36(6): 1630–1637.
Gao G L, Feng Q, Zhang X Y, et al. 2017. Review on modeling evapotranspiration of land surface based on the evapotranspiration models and micro-meteorological data[J]. Plateau Meteor, 36(6): 1630–1637.
DOI:10.7522/j.issn.1000-0534.2016.00115 |
|
郭晨露, 马耀明, 马伟强, 等. 2017. 青藏高原珠峰地区戈壁下垫面上实际蒸散发量和蒸发皿蒸发量的关系研究[J]. 高原气象, 36(1): 79–86.
Guo C L, Ma Y M, Ma W Q, et al. 2017. Relationship between the actual evapotranspiration and pan evaporation in the Gobi land surface of the Qomolangma region of the Qinghai-Xizang Plateau[J]. Plateau Meteor, 36(1): 79–86.
DOI:10.7522/j.issn.1000-0534.2016.00020 |
|
吉喜斌, 康尔泗, 赵文智, 等. 2005. 黑河中游典型灌区水资源供需平衡及其安全评估[J]. 中国农业科学, 38(5): 974–982.
Ji X B, Kang E S, Zhao W Z, et al. 2005. Analysis on supply and demand of water resources and evaluation of the security of water resources in irrigation region of the middle reaches of Heihe River, Northwest China[J]. Scientia Agricultura Sinica, 38(5): 974–982.
|
|
刘波, 马柱国, 丁裕国. 2006. 中国北方近45年蒸发变化的特征及与环境的关系[J]. 高原气象, 25(5): 840–848.
Liu B, Ma Z G, Ding Y G. 2006. Characteristics of the changes in pan evaporation over northern China during the past 45 years and the relations to environment factors[J]. Plateau Meteor, 25(5): 840–848.
|
|
刘昌明, 孙睿. 1999. 水环境的生态学方面:土壤-植被-大气系统水分能量平衡研究进展[J]. 水科学进展, 10(3): 251–259.
Liu C M, Sun R. 1999. Ecological aspects of water cycle:Advances in soil-vegetation-atmosphere of energy and water fluxes[J]. Adv Waterence, 10(3): 251–259.
|
|
刘昌明, 张丹. 2011. 中国地表潜在蒸散发敏感性的时空变化特征分析[J]. 地理学报, 66(5): 579–588.
Liu C M, Zhang D. 2011. Temporal and spatial change analysis of the sensitivity of potential evapotranspiration to meteorological influencing factors in China[J]. Acta Geographica Sinica, 66(5): 579–588.
DOI:10.11821/xb201105001 |
|
钱正安, 宋敏红, 吴统文, 等. 2017. 世界干旱气候研究动态及进展综述(Ⅱ):主要研究进展[J]. 高原气象, 36(6): 1457–1476.
Qian Z A, Song M H, Wu T W, et al. 2017. Review on advances in world dryland climate research(Ⅱ):Main investigation progress[J]. Plateau Meteor, 36(6): 1457–1476.
DOI:10.7522/j.issn.1000-0534.2017.00076 |
|
任鹏程, 2013. 不同蒸发皿比较及中国北方冬季20cm口径蒸发皿蒸发量变化趋势分析[D]. 兰州: 兰州大学.
Ren P C, 2013. Analysis of different evaporation pans and long term trend of 20 cm pan evaporation in northern china in winter[D]. Lanzhou: Lanzhou University.
http://cdmd.cnki.com.cn/Article/CDMD-10730-1013237382.htm |
|
王梅, 王建波, 那景坤. 2004. E-601型蒸发器水面蒸发实验分析[J]. 黑龙江大学工程学报, 31(3): 10–12.
Wang M, Wang J B, Na J K. 2004. Analysis on test of the surface evaporation for the E-601 type of evaporator[J]. Journal of Heilongjiang Hydraulic Engineering College, 31(3): 10–12.
|
|
夏依木拉提·艾依达尔艾力, 黄梅. 2011. 天山西部地区E-601型蒸发器与20cm口径蒸发皿观测资料对比分析[J]. 水文, 31(4): 76–80.
Aydaraili X, Huang M. 2011. Comparative analysis of observed data between E-601 evaporator and 20 cm pan in Tianshan River Basin[J]. J China Hydrol, 31(4): 76–80.
|
|
谢贤群, 王菱. 2007. 中国北方近50年潜在蒸发的变化[J]. 自然资源学报, 22(5): 683–691.
Xie X Q, Wang L. 2007. Changes of potential evaporation in Northern China over the past 50 years[J]. J Natural Resour, 22(5): 683–691.
DOI:10.11849/zrzyxb.2007.05.002 |
|
谢志鹏, 胡泽勇, 刘火霖, 等. 2017. 陆面模式CLM4.5对青藏高原高寒草甸地表能量交换模拟性能的评估[J]. 高原气象, 36(1): 1–12.
Xie Z P, Hu Z Y, Liu H L, et al. 2017. Evaluation of the surface energy exchange simulations of land surface model CLM4.5 in alpine meadow over the Qinghai-Xizang Plateau[J]. Plateau Meteor, 36(1): 1–12.
DOI:10.7522/j.issn.1000-0534.2016.00012 |
|
尹云鹤, 吴绍洪, 戴尔阜. 2010. 1971-2008年我国潜在蒸散时空演变的归因[J]. 科学通报, 55(22): 2226–2234.
Yin Y H, Wu S H, Dai E F. 2010. Determining factors in potential evapotranspiration changes over China in the period 1971-2008[J]. Sci Bull, 55(22): 2226–2234.
|
|
张士锋, 王翠翠, 孟秀敬, 等. 2013. 永定河北京段蒸散发研究[J]. 地理科学进展, 32(4): 580–586.
Zhang S F, Wang C C, Meng X J, et al. 2013. Evaporation study in Beijing Section of the Yongding River[J]. Progress in Geography, 32(4): 580–586.
DOI:10.11820/dlkxjz.2013.04.010 |
|
张有芷. 1999. 我国水面蒸发实验研究概况[J]. 人民长江, 30(3): 6–8.
Zhang Y Z. 1999. Survey of experimental study on water surface evaporation in China[J]. Yangtze River, 30(3): 6–8.
|
|
祝昌汉. 1982. 再论总辐射的气候学计算方法(一)[J]. 大气科学学报(1): 196–206.
Zhu C H. 1982. A further discussion on the climatological calculating method of total radiation(One)[J]. Journal of Nanjing Institute of Meteorology(1): 196–206.
|
|
左德鹏, 徐宗学, 刘兆飞. 2009. 基于气温的潜在蒸散发量估算方法在我国西北干旱地区的应用比较[J]. 干旱区资源与环境, 23(10): 123–131.
Zuo D P, Xu Z X, Liu Z F. 2009. Comparison of temperature-based methods for estimating potential evapotranspiration in the arid region of Northwest China[J]. J Arid Land Resour Environ, 23(10): 123–131.
|
|
左洪超, 李栋梁, 胡隐樵, 等. 2005. 近40 a中国气候变化趋势及其同蒸发皿观测的蒸发量变化的关系[J]. 科学通报, 50(11): 1125–1130.
Zuo H C, Li D L, Hu Y Q, et al. 2005. Characteristics of climatic trends and correlation between pan-evaporation and environmental factors in the last 40 years over China[J]. Sci Bull, 50(11): 1125–1130.
DOI:10.3321/j.issn:0023-074X.2005.11.012 |
2. University of Chinese Academy of Sciences, Beijing 100049, China
 2018, Vol. 37
2018, Vol. 37
