1 引言

随着中国经济的飞速发展, 气象灾害给经济和人民的生命财产造成的影响越来越大。例如, 2008年我国南方地区长时间的雨雪冰冻天气、2012年北京“7·21”特大暴雨、2014年建国以来最强台风“威马逊”袭击华南、2016年“BOSS级”寒潮影响我国大部分地区。目前, 气象部门对于一周之内的天气过程能够较准确的预报出来, 但对一周之后的天气的预报仍然存在着很大的困难, 同时对天气过程的持续性和可能导致的气象灾害也较难预测(金荣花等, 2010; 伍荣生等, 2007)。在全球变暖背景下, 极端天气出现的频率越来越高, 气象灾害造成的损失越来越大(丑纪范, 2012), 需要气象部门能够更早的预报出来, 为政府防灾减灾提供依据。

随着对气候系统研究的不断深入, 如ISO(Intraseasonal Oscillation), MJO (Madden-Julian Oscillation), 平流层和对流层的相互作用等(Baldwin et al, 2003; Wheeler et al, 2004), 以及计算机性能的提高、资料同化技术的发展、集合预报的发展、模式耦合技术的提高(Woolnough et al, 2007; Overpeck et al, 2011; Sue, 2008), 都为提高延伸期预报技巧提供了有利条件。欧洲中期天气中心ECMWF (The European Centre for Medium-Range Weather Forecasts)(Vitart, 2004)、东京气候中心TCC (Tokyo Climate Center)和美国气候预测中心CPC (Climate Prediction Center)(Saha et al, 2005)等业务中心都已开展了业务的月预报应用。2014年国家气候中心也发布了第二代月动力延伸预报模式系统DERF2. 0 (National Climate Centre second-generation monthly Dynamic Extended Range Forecast operational system 2. 0), 该模式较DERF1. 0模式极大的改进了资料同化处理, 大大提高了产品的空间分辨率(Wu et al, 2010; 丁一汇等, 2002, 2004; 顾伟宗等, 2009; 陈桂英等, 1998)。国内的很多学者也针对模式做了很多研究, 陈官军等(2010)利用NCEP/CFS模式1981—2004年的历史回报试验结果, 检验了该系统对夏季东亚系统大气环流的预报技巧和系统误差, 结果表明预报的可靠时效在5天左右, 系统性误差随着预报时间的延长而增加, 10天以上的误差趋于稳定。庄照荣等(2010)分析了GRAPES全球模式的模式误差, 发现模式误差随着分辨率降低而线性增加, 模式误差随着预报时效的增加呈现线性增长的趋势。唐红玉等(2016)利用2010—2014年DERF2. 0模式500 hPa的数据, 试验了4个关键区和5种统计降尺度方法, 对重庆2010—2015年2月气温和2010—2014年8月降水量进行了回报预测和检验。何慧根等(2014)利用DERF2. 0模式1982—2010年的回报试验结果, 检验了DERF2. 0对中国气温和降水各月的预测效果。单机坤等(2016)利用国家气候中心第一代海气耦合模式, 采用逐步回归的统计降尺度方法, 建立了针对我国冬季极端低温日数的动力-统计降尺度预测方法。孟纯纯等(2016)利用欧洲中期天气中心(ECMWF)的在分析资料和区域大气模式RAMS对2008/2009年秋冬季节的干旱事件进行了数值模拟, 取得了较好的模拟效果。

我国中纬度地区春季冷空气活动仍然比较频繁, 冷空气南下会引起温度明显下降, 时常发生晚霜冻和倒春寒等灾害, 因此最低温度是春季关注的重要要素之一(叶殿秀等, 2008; 翟盘茂等, 1997; 陈乾金等, 1995; 马柱国, 2003)。这段时间是农作物成长的重要时期, 这些灾害严重影响农作物的生长, 从而影响产量(李茂松等, 2005; 冯玉香等, 1999)。比如3月小麦陆续进入拔节期, 冬小麦进入拔节期后抗霜冻能力迅速下降(Zhang et al, 2011; 钟秀丽等, 2007), 2004年黄淮地区受冻害的小麦面积约333×10⁴ hm², 严重冻害超过33. 3×10⁴ hm², 严重影响了当年的小麦产量。在3月最低温度的预报显得格外重要, 如果能提前预报出较长时间较明显的降温过程, 提前做好预防措施, 对于减少冷空气对农作物的影响非常重要。

本研究利用DERF2. 0模式1983—2013年20个全样本集合平均的最低温度数据, 对我国中纬度地区3月最低温度的预报能力进行评估和分析, 为DERF2. 0模式在业务中的使用提供参考。

2 研究区域和数据

研究区域为我国中纬度地区105°E—117°E, 30°N—40°N, 共143个格点。模式数据选用的是国家气候中心第二代月动力延伸预报模式系统(DERF2. 0)1983—2013年的历史回算数据, 20个全样本集合平均的最低温度逐日数据, 时间是3月1—31日, 空间分辨率为1°×1°, 预报时效是1~52天。观测资料选用的是国家信息中心的“中国国家级地面气象站均一化气温格点数据集”中的日最低气温数据, 空间分辨率为0. 5°×0. 5°。由于空间分辨率不同, 将观测资料四个格点的值进行平均, 作为格点的值。

3 集合经验模态分解方法EEMD

Huang et al(1998)于1998年提出了经验模态分解EMD (Empirical Mode Decomposition), 这是一种分析非线性非平稳时间序列的新方法。EMD的表达式为:

$ X\left(t \right) = \sum\limits_{j = 1}^n {{C_j} + {r_n}}, $

(1)

式中: X(t)为原时间序列; C_j(j=1, 2, …, n)为分解后的IMF分量; r_n为趋势项。通过EMD可以将时间序列里面的本征模态函数IMF (Intrinsic Mode Function)分量逐级分离出来, 并求其Hilbert谱, 通过分析IMF分量及相应的谱, 可得知原序列的多尺度振荡特征。但通过EMD分解出来的IMF分量经常包含尺度相近的信号, 出现模态混合。模态混合使某些IMF分量的特征时间尺度不明确, 一个分量往往包含不同的时间尺度。为了消除模态混合, 使时间尺度的特征更加清晰, Huang et al(2008)在经验模态分解(EMD)的基础上进行了改进, 发展了集合经验模态分解EEMD(Ensemble Empirical Mode Decomposition)。EEMD是对原始的时间序列加入噪声, 经过EMD分解之后, 分解为多组IMF分量, 它既有原有时间序列的EMD成分, 也有包含噪声的EMD成分; 把这些IMF分量进行平均, 就可以把噪声的EMD成分抵消掉。EEMD在很大程度上解决了模态混合问题, 避免了IMF分量尺度混杂, 使其能够更好的表现出它所反映的时间尺度。

4 结果分析 4.1 预报能力评估

DERF2. 0的预报时效为1~52天, 使用的数据是1983—2013年3月1—31日的最低温度逐日数据, 数据每天都有52个预报值。对区域中143个格点1983—2013年每年3月每天的52个预报值进行检验, 计算绝对误差的绝对值AE和均方根误差RMSE, 然后求平均值。

$ \begin{array}{l} AE\left(t \right) = \\ \;\;\;\;\;\;\;\;\;\;\frac{{\sum\nolimits_{i = 1}^{143} {\sum\nolimits_{j = 1983}^{2013} {\sum\nolimits_{k = 1}^{31} {\left| {T{1_{ijk}}\left(t \right) - T{2_{ijk}}\left(t \right)} \right|} } } }}{{143 \times 31 \times 31}}, \end{array} $

(2)

式中: AE(t)(t=1, 2, …, 52)为每个预报时次的绝对误差的绝对值, 共52个; i= 1, 2, …, 143, 共143格点; j=1983, 1984, …, 2013, 从1983—2013年, 共31年; k=1, 2, …, 31, 3月1-31日, 共31天; T1为最低温度模式预报值; T2为最低温度观测值。

$ \begin{array}{l} RMSE\left(t \right) = \\ \frac{{\sum\nolimits_{i = 1}^{143} {\sum\nolimits_{j = 1983}^{2013} {\sqrt {{{\sum\nolimits_{k = 1}^{31} {\left[ {T{1_{ijk}}\left(t \right) - T{2_{ijk}}\left(t \right)} \right]} }^2}/31} } } }}{{143 \times 31}}, \end{array} $

(3)

式中: RMSE(t)(t=1, 2, …, 52)为每个预报时次的均方根误差, 共52个; i=1, 2, …, 143, 共143格点; j=1983, 1984, …, 2013, 从1983—2013年, 共31年; k=1, 2, …, 31, 3月1—31日, 共31天; T1为最低温度模式的预报值; T2为最低温度的观测值。

利用1983—2013年每年相同预报时次的最低温度模式预报值和最低温度观测值分别组成时间序列, 并求两者的相关系数R。

$ \begin{array}{l} R\left(t \right) = \sum\nolimits_{i = 1}^{143} {\sum\nolimits_{j = 1}^{31} {{\rm{Cov}}\left[ {T{1_{ij}}\left(t \right), T{2_{ij}}\left(t \right)} \right]} } \\ \;\;\;\;\;\;\;\;\;\;/\sqrt {{\rm{Var}}\left[ {T{1_{ij}}\left(t \right)} \right] \times {\rm{Var}}2\left(t \right)} /\left({143 \times 31} \right), \end{array} $

(4)

式中: R(t)(t=1, 2, …, 52), 每个预报时次的相关系数, 共52个; i=1, 2, …, 143, 共143格点; j=1, 2, …, 31, 3月1—31日, 共31天; T1(t) (t=1, 2, ……, 52), 1983—2013年预报时次t最低温度模式预报值的时间序列; T2(t=1, 2, …, 52), 1983—2013年预报时次t最低温度观测值的时间序列; Cov[T1_ij(t) T2_ij(t)]为T1_ij(t)和T2_ij(t)的协方差; Var[T1_ij(t)]为T1_ij(t)的方差; Var[T2_ij(t)]为T2_ij(t)的方差。

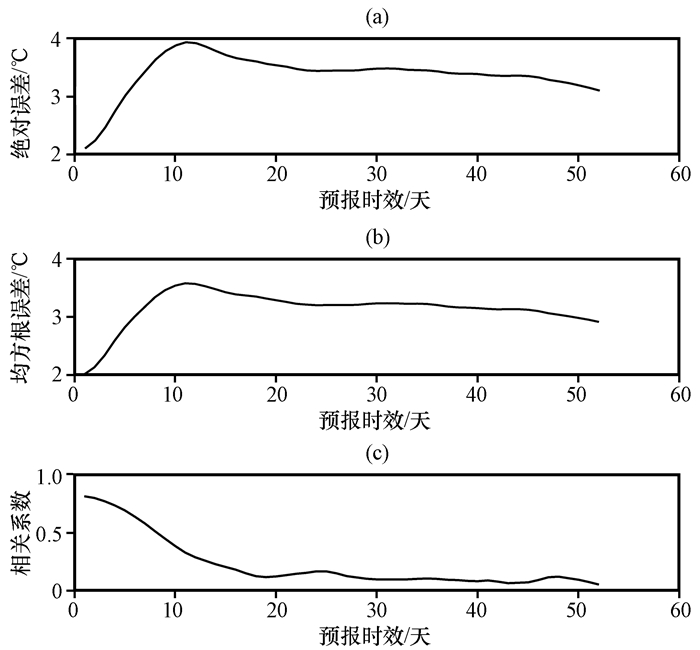
利用上述方法计算出绝对误差的绝对值AE、均方根误差RMSE和相关系数R在不同预报时效的平均值(图 1)。由图 1可以看出, 绝对误差的绝对值和均方根误差开始随着预报时效的增加而变大, 在第11天达到最大, 之后开始缓慢下降。相关系数大致也是随着预报时效增大而降低, 第1~10天都可以通过95%的显著性检验, 在第11天为0. 328 7, 没有通过95%的显著性检验。因此, DERF2. 0最低温度的预报时效前10天可信度较高, 并且在前10天中随着预报时效增大, 误差也逐渐增大, 预报时效越短, 可信度越高, 超过10天的预报可信度越来越低。

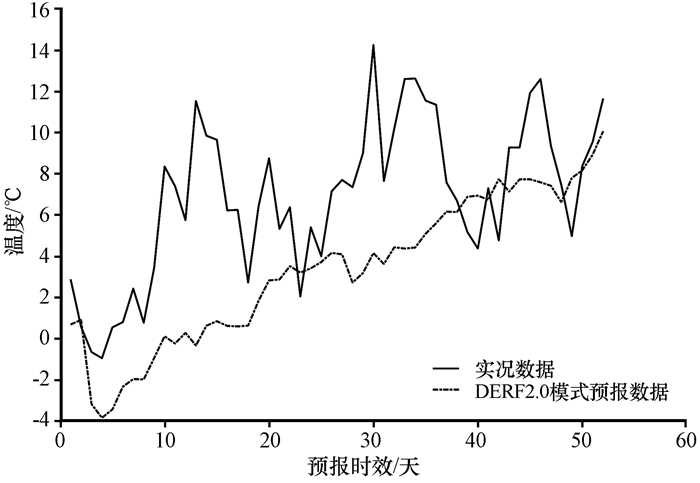
为什么绝对误差的绝对值和均方根误差在第11天达到最大之后并没有随着相关系数的减小而增大, 而是缓慢下降, 为了更加直观的分析原因, 选取113°E、35°N这个格点, 采用2002年3月1日的DERF2. 0的1~52天预报数据, 并和实况数据进行对比(图 2)。先来分析相关系数, 相关系数表示两个变量之间的线性相关程度。首先看前10天, 由图 2可以看到, 3月1—4日的降温过程、5—7日的升温过程和8—10日的升温过程, 模式数据均能反映出来, 也就是模式数据和实况数据的变化比较一致, 因此两者的相关程度比较高, 相关系数也就比较高。再看预报时效的第11~20天, 其中10—13日的降温升温过程、14—20日的降温过程只能够大体反映出来, 相关程度并不是特别高, 相关系数也就较前10天低。最后看预报时效的第20~52天, 模式数据和实况数据的变化越来越不一致, 有时甚至变化相反, 两者基本没有什么相关性了, 相关系数也就比较低。接下来分析绝对误差的绝对值AE和均方根误差RMSE, 这两者都是反映了模式数据偏离实况数据的程度。先看预报时效的第1~11天, 可以看出随着时间的增长, 模式数据越来越偏离实况数据, 因此绝对误差的绝对值AE和均方根误差RMSE在1~11天内逐渐增大, 并且在第11天达到了最大值。再看预报时效的第12~52天, 模式数据并没有随着时间的增长而越来越偏离实况数据, 而是呈现出在实况数据上下来回波动的特点, 因此绝对误差的绝对值AE和均方根误差RMSE并没有像想象中那样随着预报时间的增长而增大, 反而逐渐减小并且趋于稳定。经过以上的分析可知, 随着时间的增长, 模式数据和实况数据的变化越来越不一致, 相关系数也就越来越低; 而模式数据在第11天之后并没有随着时间的增长而越来越偏离实况数据, 而是呈现出在实况数据上下来回波动的特点, 因此绝对误差的绝对值AE和均方根误差RMSE并没有随着预报时间的增长而增大, 反而逐渐减小并且趋于稳定。但这并不能表示11天之后的预报效果好, 因为它并不能反映出升温和降温过程, 仅仅是模式预测值并没有偏离实况太多而已。由于图 2是选取的其中1天的1个格点作为示例, 和图 1计算了所有格点31年的数据的平均值会有出入。

为了进一步探讨模式在不同预报时效的效果不同的原因, 下一步将采用EEMD的方法对模式和观测资料进行分解对比。

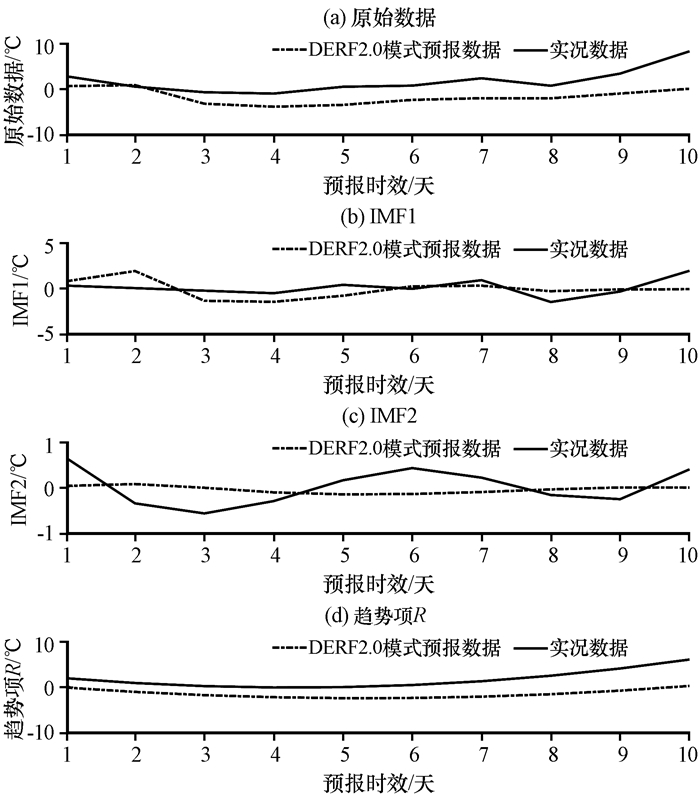
4.2 不同预报时段的EEMD分析

为了进一步分析DERF2. 0模式和观测数据, 采用EEMD方法进行分析, 由于前10天的预报效果较好, 先从前10天开始分析。选取113°E、35°N这个格点, 采用2002年3月1日的DERF2. 0的前10天预报数据, 对其进行EEMD分析(图 3)。DERF2. 0数据和观测数据按照时间尺度不同被分解为高频分量IMF1、低频分量IMF2和趋势项R三项, IMF1、IMF2和R相加即为原始数据。DERF2. 0各项的方差贡献率为52. 15%, 0. 31%和47. 54%, 观测数据各项的方差贡献率为16. 55%, 3. 27%和80. 18%。DERF2. 0数据和观测数据都是以高频分量IMF1和趋势项R为主, 低频分量IMF2占的比重较少。从图 3中可以看出, DERF2. 0模式和观测数据的高频分量IMF1是高频波动, 能够反映出升温和降温过程, 而趋势项R则反映出这段时间的温度变化整体趋势, 低频分量IMF2表示升温和降温一些大的波动, 占的比重较少, 可以忽略。

为了进一步分析DERF2. 0数据在各个预报时段的预报能力, 将1~52天分为了5个预报时段, 对区域内所有格点1983—2013年3月的最低温度数据不同预报时效进行了EEMD分析, 并计算了平均方差贡献率(表 1)。在预报效果最好的前10天, DERF2. 0的趋势项R的方差贡献率比观测数据趋势项R的方差贡献率高了11. 3%, 高频分量IMF1和低频分量IMF2各低了5%左右。预报时间超过10天之后DERF2. 0高频分量IMF1的方差贡献率下降了17%左右, 而趋势项增加了17%左右, 低频分量IMF2的变化不大。可见DERF2. 0模式在10天之后预报能力下降的主要原因是高频分量IMF1的预报能力下降, 10天之后DERF2. 0模式高频分量IMF1的方差贡献率只有观测数据的一半, 意味着预报的升温降温过程比实况少了一半。升温降温过程预报的数量少, 再加上升温降温过程预报时间的差异, DERF2. 0模式10天以后的预报能力大大下降。

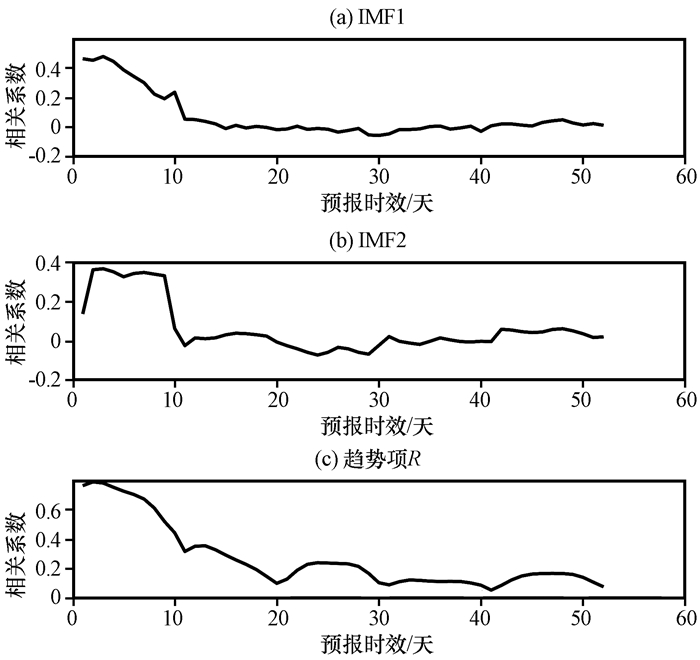
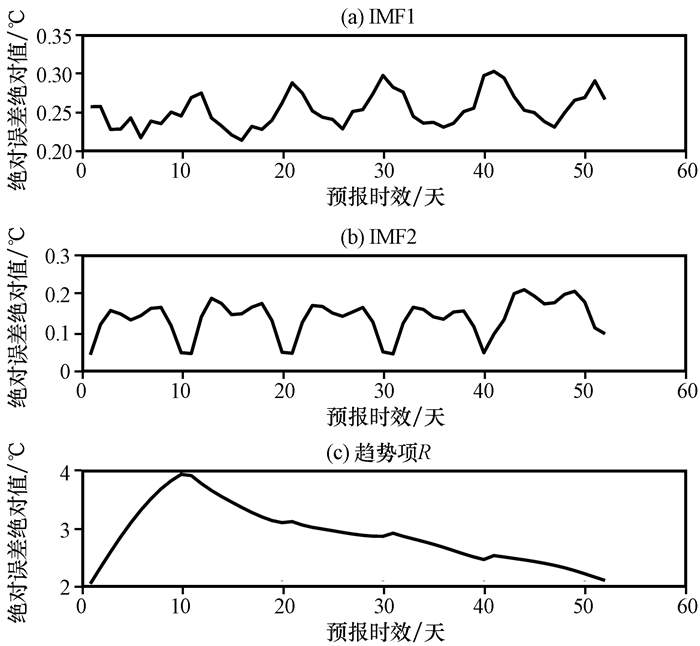
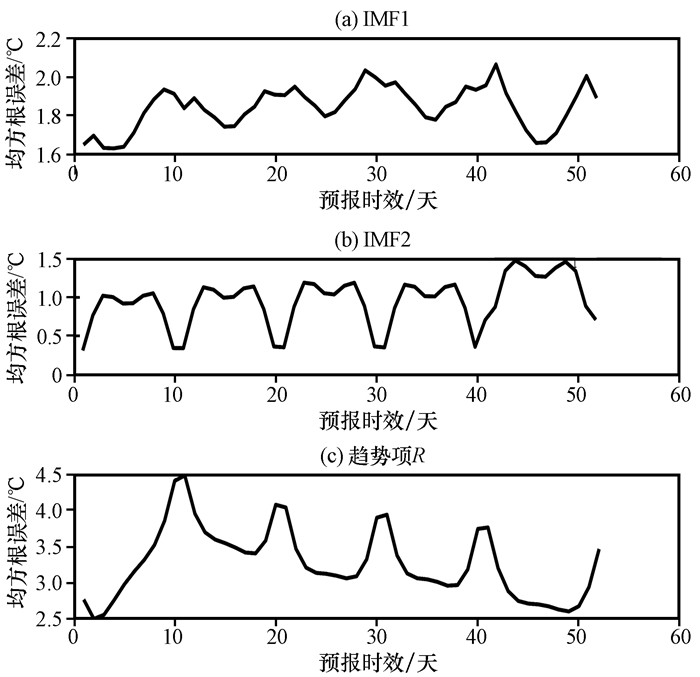
为了更好的分析DERF2. 0模式的预报能力, 将对各个分量的相关系数、绝对误差的绝对值和均方根误差进行分析。在对1~52天整体数据进行EEMD分解之后发现, 由于时间序列较长, 趋势项R的方差贡献率占90%以上, 其他高频项和低频项占的比重过低, 不能反映出问题。于是将1~52天分为了5个预报时段(与表 1的预报时段一致), 分别进行EEMD分解并计算了各个分量的相关系数、绝对误差的绝对值和均方根误差, 计算后将它们合到一起(图 4~6)。图 4中, 高频项IMF1相关系数在1~10天随着预报时效增加而降低, 11天之后趋近于0。在前10天中, 第1~6天通过了95%的显著性检验, 在第7天为0. 301 9, 没有通过95%的显著性检验。DERF2. 0模式高频分量也就是反映升温降温过程在前6天可信度较高, 在11天之后相关系数趋近于0, 升温降温过程预测的参考意义已经不大了。低频项IMF2第1天到第2天有个显著增加, 之后一直保持平稳, 并且通过了95%的显著性检验, 到了第10天趋近于0, 之后也一直在0附近。趋势项R呈现出随着预报时效增加而减少的趋势, 第1天到第13天除了第11天, 其他都通过了95%的显著性检验, 在第14天为0. 325 3, 没有通过95%的显著性检验。趋势项R反映了升温和降温的趋势, 它的相关性整体上好于高频和低频项, 预测的有效时间也较长。图 5和图 6中, 高频项IMF1和低频项IMF2的绝对误差的绝对值和均方根误差比较类似, 在相关系数通过95%的显著性检验的第1~6天中, 呈现出有增有减的波动状态, 在第7天之后, 并没有因为相关系数的降低而一直增加, 即便是在11天之后相关系数趋近于0, 也是如此, 呈现出一种波动的状态。趋势项R的绝对误差的绝对值在第10天达到最大之后便一直下降, 均方根误差则在第11天达到最大值之后呈现出波动状态。尽管趋势项R比高频项IMF1和低频项IMF2的相关系数要要高, 但趋势项R的误差比高频项IMF1和低频项IMF2的误差偏大。在上文预报能力评估的分析中, 已经知道模式数据并没有随着时间的增长而越来越偏离实况数据, 而是呈现出在实况数据上下来回波动的特点, 因此经过EEMD分解的各个分量的绝对误差的绝对值和均方根误差并没有随着预报时间的增长而增大, 而是呈现出一种波动的特点。

4.3 EEMD逐年分析

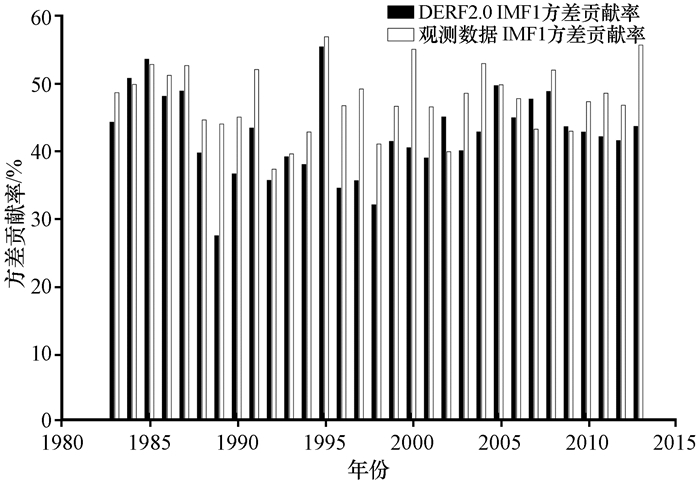
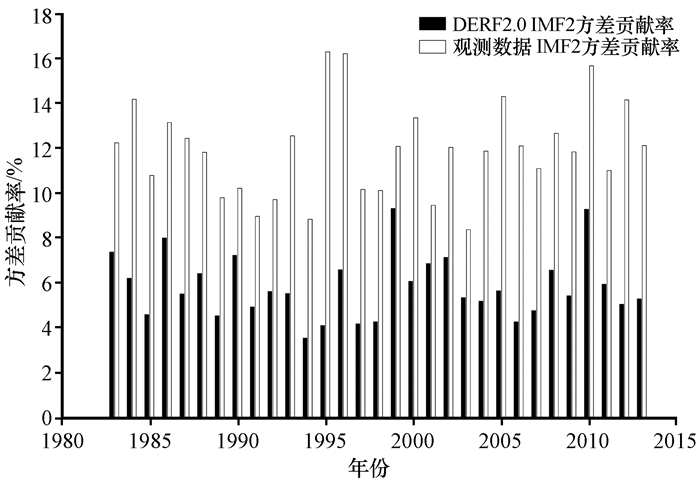
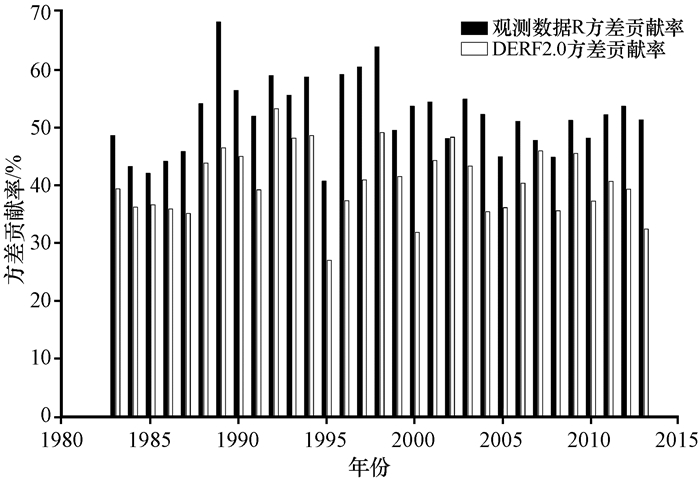
由于DERF2. 0模式在前10天的预报能力较好, 将分析重点放到前10天上面, 分析它在每年的表现情况, 评价它的稳定性。接下来, 对DERF2. 0模式预报时效10天的数据和观测数据进行逐年的EEMD分析, 得到各个方差分量随年份的变化(图 7~9)。通过图 7~9可以看出, 1989, 1996, 1997, 2000, 2004和2013年各个分量方差贡献率差距较大, 高频分量IMF1少10%左右, 低频分量IMF2少5%左右, 趋势项R多了15%左右。DERF2. 0模式历年高频分量IMF1方差贡献率和观测数据相比普遍偏低, 只有1984, 1985, 2002, 2007和2009年这5年偏高; DERF2. 0模式历年低频分量IMF2方差贡献率和观测数据相比每年都偏低; DERF2. 0模式历年趋势项R方差贡献率和观测数据相比每年都偏高。DERF2. 0模式预报时效10天的数据整体上每年各项的方差贡献率还是比较稳定, 每年都是高频分量IMF1方差贡献率较低, 趋势项R方差贡献率较高。这也就导致升温降温过程预报的次数普遍比实况偏少, 很少出现偏多的情况。可以看出DERF2. 0模式的问题不是升温降温过程预报多了, 而是少了。

5 结论与讨论

经过对中纬度地区DERF2. 0模式3月份最低温度的预报能力评估以及EEMD分析, 得到以下主要结论:

(1) DERF2. 0最低温度前10天预报可信度较高, 超过10天预报的可信度越来越低。并且在前10天中随着预报时效增大, 误差也逐渐增大, 预报时效越短, 可信度越高, 超过10天的预报可信度越来越低。

(2) 经过EEMD分析发现DERF2. 0模式和观测数据的高频分量IMF1和趋势项R为主要分量高频分量, 低频分量IMF2占的比重较少, 可以忽略。IMF1是高频波动, 能够反映出升温和降温过程, 而趋势项R则反映出这段时间的温度变化整体趋势, 低频分量IMF2表示升温和降温一些大的波动。

(3) DERF2. 0模式在10天之后预报能力下降的主要原因是高频分量IMF1的预报能力下降, 10天之后DERF2. 0模式高频分量IMF1的方差贡献率只有观测数据的一半, 意味着预报的升温降温过程比实况少了一半。高频分量IMF1在前6天的预报可信度较高, 低频分量IMF2在前9天的预报可信度较高, 趋势项R则在前13天预报可信度较高。高频分量IMF1的预报能力较低频分量IMF2和趋势项R较弱, 也就是升温降温过程预报能力较弱。趋势项R的误差比高频项IMF1和低频项IMF2的误差偏大。

(4) DERF2. 0模式和实况的误差以及DERF2. 0模式经过EEMD分解后各个分量的误差在10天之后并没有随着预报时效的增加而一直增大, 这并不能说明它的预报能力在10天之后比较好, 是因为模式数据并没有随着时间的增长而越来越偏离实况数据, 而是在实况数据上下来回波动。10天之后DERF2. 0模式对升温降温过程的预报能力较差, 但是数值没有偏离实况值太多。

(5) 通过EEMD分析DERF2. 0模式前10天预报历年的结果, 发现各项方差贡献率年际变化不大, 比较稳定。总体上看高频分量IMF1和低频分量IMF2方差贡献率和观测数据相比普遍偏低, 趋势项R方差贡献率和观测数据相比每年都偏高。

DERF2. 0模式存在的普遍问题是高频分量IMF1和低频分量IMF2方差贡献率和观测数据相比普遍偏低, 趋势项R方差贡献率和观测数据相比偏高以及高频分量IMF1的预报能力偏低。模式误差可以分为系统误差和非系统误差, 误差是由初始场的不准确, 模式对对实际大气过程的描述出现的误差以及大气的混沌特性造成的。趋势项R的误差反应了模式气候态相对于实际气候态的漂移, 属于系统性误差, 而高频分量IMF1和低频分量IMF2的误差属于非系统误差。DERF2. 0模式在未来的发展中, 需要提高观测数据的质量, 改善资料同化技术, 加强对大气过程的研究, 改进物理过程的参数化方案不断的完善和发展DERF2. 0模式。今后在对DERF2. 0模式的使用中, 可以利用历史观测资料, 采用相应的统计方法, 发展误差订正技术, 将系统性误差(趋势项R的误差)和非系统性误差(高频分量IMF1和低频分量IMF2的误差)采用不同的方法分开进行订正, 提高模式的预报准确性。