2. 内河航运技术湖北省重点实验室, 湖北 武汉 430063;
3. 国家水运安全工程技术研究中心, 湖北 武汉 430063;
4. 武汉理工大学资源与环境工程学院, 湖北 武汉 430070
2011年以来, 受国家经济结构调整和能源政策改革影响, 中国可再生能源发电能力正呈现出快速发展趋势(李芬等, 2013)。2016年底, 中国可再生能源发电装机容量已达5.7亿千瓦, 占全部电力装机容量的34.6%, 其中, 风力发电装机容量达1.5亿千瓦, 占可再生能源装机容量比例超过20%, 同时占全球风力发电装机容量的34.7%, 装机容量已位居全球第一(国家能源局, 2017)。与常规电力发电相比, 风电具有较强的随机性、间歇性和不可控性等基本特征(Johnson, 2006)。根据国家能源局统计数据, 2016年中国风电发电量2 410亿千瓦时, 全国风电平均利用小时数1 742 h, 全年弃风电量497亿千瓦时, 装机容量与发电量的增速呈现出巨大反差。以风电产业大省甘肃省为例, 该省已成为全国弃风最严重的地区, 弃风率达43%、弃风电量104亿千瓦时, 平均利用小时仅有1 088 h(国家能源局, 2016)。为提高风能可利用率, 甘肃省多家风电场布设了湖北省气象服务中心研发的“风功率预测预报系统”和北京市气象局开发的北京快速循环更新同化系统(Beijing Rapid Update Cycle, BJ-RUC)数值预报产品, 专门用于提高弃风限电背景下的风电场风力预测精度(陈正洪, 2013;刘丽珺等, 2016)。但通过评估发现, 24 h短期预测的月均方根误差率多大于20%, 无法满足国家能源局和国家电网最新联合颁布的《国家能源行业标准(NB/T 31046-2013):风电功率预测系统功能规范》(国家能源局, 2014)。提高短期风能数值预报产品的准确率已成为弃风限电背景下提高风能利用率的核心问题, 亟需发展高精度和可具推广性的评估预测方法。
传统的风功率预测方法主要强调开发基于物理过程建模的预测模型(Lundtang et al, 1997; Foley et al, 2012), 包括: (1)多尺度(全球-区域-局地)耦合建模, 着重开发升尺度、降尺度方法和集合预报等数值预测方法; (2)统计方法和机器学习相结合的预测方法; (3)基准技术和不确定性联合分析方法。选择具体方法时主要取决于预测规模和项目要求。从风电业务化运行的实际需求看, 还要强调预测方的精度和稳定性:一是基于统计方法的风电功率预测, 一般适用于长期预报(Doucoure et al, 2016;张双益等, 2017);二是基于天气预报模式的风电功率预测, 一般考虑大气动力学过程对风电场气流的实时影响, 通常用于短期预报(Landberg, 2001;柳艳香等, 2008;王澄海等, 2011;程兴宏等, 2012;丁煌等, 2013;石岚等, 2017)。国内风电场通常要求提供3~7天的风电场数值预报, 时间分辨率为15 min。丹麦、美国、西班牙等国在风速及风电功率预测系统研发领域的技术较为成熟, 推出的WPPT、Prediktor、eWind、ARMINES等系统在全球应用广泛; 国内风电功率预测系统研发团队主要包括中国电科院、东润环能、国电南自、华北电力大学、IBM中国研究院、中国气象局、湖北省气象局、甘肃省气象局等。相关系统在风资源和风电预测中均采用集成建模方法, 以提高预测精度和数据质量。例如, 利用神经网络(Artificial Neural Network, ANN)和参考站点风速、方向观测数据的风速场分布预测(Addison et al, 2000);利用气象数值预报和Kalman滤波方法构建风速-风功率预测模型(Cassola et al, 2012);针对微尺度复杂地形特征的风电场, 还通过计算流体力学CFD(Computational Fluid Dynamics)技术改进局部地形和尾流效应对风功率预测的影响(Magnusson et al, 2001)。
甘肃省东部地区地处黄土高原核心地带, 属于典型的黄土高原沟壑区, 风力资源丰富, 风电产业发展前景广阔, 亟需发展适用于研究区的高精度、业务化运行的风场资源评估及风功率预测方法(张新科等, 2017)。Kalman滤波具有动态预测和校正能力, 模型求解时不需要存储大量数据, 一旦观测到新数据便可及时计算新的估计值, 该算法适用于在线风速预测, 难点是估计白噪声的统计特性处理(Louka et al, 2008;祝嬴等, 2012)。CFD作为传统线性模型的方法补充, 不仅可以有效地用于跨尺度风速和潜在风功率评估, 而且可以改进复杂地形下微尺度风功率预测准确率(Castellani et al, 2014), 但CFD计算时间较长, 无法满足在线计算要求。本文通过集成CFD和Kalman滤波的建模优势, 形成一个可用的集成预报模型, 并以黄土高原沟壑区微尺度的典型风电场为例, 利用集成模型对风速分区分布和风功率预报进行定量分析, 以提高短期风能数值预报产品的准确率。
2 资料选取和方法介绍 2.1 资料选取以甘肃环县南湫风电场为研究区, 环县南湫乡位于甘肃省东部偏北山区, 该风电场位于106°21′40″E-107°44′40″E, 36°01′06″N-37°09′10″N。地貌上看, 研究区处于南部残塬沟壑区向北部沙漠区的过渡地带, 海拔在1 650~2 060 m, 年降水量平均为420 mm, 日照时数为2 643 h, 平均气温6.7 ℃, 无霜期131天(王丹云等, 2017)。风电场土质属黄绵土, 为典型的黄土高原丘陵沟壑区, 区内丘陵、沟壑、梁峁交错纵横。
统计资料来源于2014年中国华电集团公司南湫风电场两种型号的风机数据: 25台额定功率2 000 kW的风机(Ⅰ期), 33台额定功率1 500 kW风机(Ⅱ期)。具体包括风电场2014年的风电机组监控数据采集控制系统(Supervisory Control and Data Acquisition, SCADA)导出的58台风机全年逐日风速、风向与功率等观测资料。SCADA是以10 min为间隔来拓展每个风力风机数据库的控制系统, 合理地考虑了风机参数(如转子风速, 机舱位置、俯仰角、有功功率等)对风场的响应和输出功率变化, 有关SCADA风力机特性和数据处理的方法较为成熟(Kusiak et al, 2011, 2013; Schlechtingen et al, 2013; Yang et al, 2013), SCADA数据检验主要关注数据合理性和完整性。首先, 参考《风电场风能资源评估方法》(GB/T 18710-2002)(国家质检总局, 2002)中有效数据的完整率和合理性指标, 对SCADA数据集进行预处理, 保证了数据连续性与完整性; 然后, 利用Matlab12.0从处理的数据集中提取各风机输出的机头风速和功率, 为保证计算效率、数据可靠性和差异性等原则, 进一步选取2014年6月每小时15 min间隔的定时风速作为完整的自记测风资料, 用于Kalman滤波建模和模型检验, 样本总数为20 554 h。
风功率模拟数据由最新版的BJ-RUC v3.0模式获取, 数据空间分辨率为9 km和3 km, 其主模式为WRF V3.5.1, 前处理模块为WPS V3.5和WRF-VAR V3.3.1;模式参数化方案包括THOMPSON显式微物理方案、ACM2边界层方案、RRTM长波辐射方案、Dudhia短波辐射方案和Noah陆面模式, 此外还耦合了UCM(Urban Canopy Model)模式及最新的土地利用数据(魏东等, 2010);模式背景场为NCEP GFS 0.5°预报场, 背景场水汽由GFS、EC和T639资料融合; 模式资料同化方法为三维变分同化, 同化资料为常规GTS资料、北京地区自动站观测、北京地区地基GPSPW、6部雷达径向风观测、6部雷达反射率因子观测并进行多重外部循环(Benjamin et al, 2004); BJ-RUC产品能提供风机轮毂高度处的风速、风向、温度、相对湿度和压强等气象要素格点资料(时间分辨率15 min, 空间分辨率9 km和3 km, 预测时间长度128 h)。研究区所处的黄土高原地区仅能获取分辨率为9 km的BJ-RUC数据, 在特殊地理位置、气候条件及复杂下垫面影响下, 模式预报精度受限(刘丽珺等, 2016), 亟需在该模式产品基础上开展本地化研究, 以提高研究区的风功率预测精度。
2.2 方法介绍 2.2.1 CFD建模CFD建模所需的初始网格模型由高程数据生成。CFD具体模拟过程是:首先利用地形高程数据建立网格文件, 并导入fluent 6.3软件; 再通过用户定义函数模块设定风速廓线分布模式及湍流模式, 并输入初始边界值; 最后选取适用于低空风场模拟的紊流模型重整化群(renormalization-group, RNG) k-ε模式进行模拟。湍流模型一般分为零方程模型、一方程模型、两方程模型和四方程模型等; 相应模拟方法有直接数值模拟(Direct Numerical Simulation, DNS)、大涡模拟(Large Eddy Simulation, LES)和雷诺平均数值模拟(Reynolds Average Navier-Stokes, RANS)。
本文关注风电场风能分布状态, 不考虑流场瞬时状态。考虑到计算量与收敛性的合理性, 选用两方程模型中的标准k-ε模型(Launder et al, 1974), 采用RANS法求解稳定的Navier-Stokes方程。
k方程:
| $ \frac{{\partial \left( {\rho k{u_i}} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_i}}}\left[ {\left( {\mu + \frac{{{\mu _\tau }}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] + {\mu _\tau }\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right)\frac{{\partial {u_i}}}{{\partial {x_j}}} - \rho \varepsilon , $ | (1) |
ε方程:
| $ \begin{array}{l} \frac{{\partial \left( {\rho k{u_i}} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _\tau }}}{{{\sigma _\varepsilon }}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right]\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + \frac{{{C_{1\varepsilon }}\varepsilon {\mu _\tau }}}{k}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right)\frac{{\partial {u_j}}}{{\partial {x_i}}} - {C_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{k}, \end{array} $ | (2) |
方程(1)和(2)等号左边为对流项, 等号右边第一项为扩散项, 第二项为产生项, 第三项为耗散项。参数含义分别为ρ为流体密度(单位: kg·m-3); k为湍流脉动动能(单位: J); ui和uj为时均速度(单位: m·s-1); μ为流体动力黏度, 是物性参数(单位: N·S·m-3); μτ为湍流粘性系数, 下标τ表示湍动流动; cμ为经验常数; ε为紊流脉动动能的耗散率(单位: %); σk和σε分别是与k和ε对应的Prandtl数; xi和xj为笛卡尔空间坐标值, 下标i, j为张量指标, 范围为(1, 2, 3)。根据张量建模原则, 当式中某指标重复出现2次及以上, 则表示要将该项在指标取值范围内遍历加和。对于直角坐标系,
假设流体不可压缩, 且为稳态, 则根据已有推荐值及实验结果, 模型常数取值分别为C1ε=1.44, C2ε=1.92, Cμ=0.09, σk=1.0, σε=1.3(Launder et al, 1974)。其中, 风速边界条件根据入口风速分布获取, 具体采用幂指数订正公式进行订正。
| $ v = {v_0}{\left( {z/{z_0}} \right)^p}, $ | (3) |
式中: z0和v0分别是观测点的观测高度和风速; P为风速订正指数; z和v分别是计算高度层的高度和该层风速, 根据本地气象资料获取。通过CFD模拟最终为Kalman滤波提供流场分区依据, 在后期的模式产品订正过程中, CFD流场模拟结果保持不变, 以便为Kalman滤波提供稳定的流场分布特征(Liu et al, 2017)。
2.2.2 Kalman滤波建模在CFD的分区基础上, 根据BJ-RUC预测的风场状况, 对现场风速分布进行分区, 并利用Kalman滤波进行风速订正处理。CFD流场模拟能够将区域中风力状况的空间分布划分成多个精细的子区域, 并精确地计算总发电量。通过集成CFD与Kalman滤波模型, 获取可用于标准功率曲线计算的输入变量, 进而估计风功率输出。在CFD确定的风场子区域内, 将BJ-RUC的预报风速和实测功率作为Kalman滤波模型的输入变量, 订正风速为输出变量。以Kalman滤波递推公式为建模基础进行计算(陆如华等, 1997)。
| $ {{\hat Y}_t} = {X_t}{{\hat \beta }_{t - 1}}, $ | (4) |
| $ {R_t} = {C_{t - 1}} + W, $ | (5) |
| $ {\sigma _t} = {X_t}{R_t}X_t^T + V, $ | (6) |
| $ {A_t} = {R_t}X_t^T\sigma _t^{ - 1}, $ | (7) |
| $ {{\hat \beta }_t} = \hat \beta _t^{ - 1} + {A_t}\left( {{Y_t} - {{\hat Y}_t}} \right), $ | (8) |
| $ {C_t} = {R_t} - {A_t}{\sigma _t}A_t^T, $ | (9) |
式中:
| $ W \approx \left( {\begin{array}{*{20}{c}} {\frac{{{{\left( {\Delta \beta } \right)}^2}}}{{\Delta T}}}&0& \cdots &0\\ 0&{\frac{{{{\left( {\Delta \beta } \right)}^2}}}{{\Delta T}}}& \cdots &0\\ \cdots&\cdots&\cdots&\cdots \\ 0&0& \cdots &{\frac{{{{\left( {\Delta \beta } \right)}^2}}}{{\Delta T}}} \end{array}} \right), $ | (10) |
| $ V \approx \left( {\begin{array}{*{20}{c}} {\frac{{{q_1}}}{{k - m - 1}}}&0& \cdots &0\\ 0&{\frac{{{q_2}}}{{k - m - 1}}}& \cdots &0\\ \cdots&\cdots&\cdots&\cdots \\ 0&0& \cdots &{\frac{{{q_n}}}{{k - m - 1}}} \end{array}} \right), $ | (11) |
式中: qi(i=1, 2, …, n)为利用资料样本建立回归方程后的残差; k为样本数。
2.2.3 发电效益评估风机的发电量输出由进风速度、风机机构设计和控制策略等因素决定(Song et al, 2015)。风机具有额定风速、额定功率输出和切断风速等基本特征, 发电效率评估中必须考虑。具体引入风机功率曲线评估风机的平均风力发电输出。当进风速度低于额定转速时, 风机输出功率与进风速度成正比; 当风速在额定转速和切断风速范围内时, 功率输出保持相同; 当风速高于切断风速时, 为保证风机安全, 需要关闭风机并使功率输出降为零。在多风机风电场中, 应根据不同类型功率曲线计算风机功率输出和电量输出。
(1) 理想状态下, 风电场总功率输出是所有风机的总和, 可得到风电场风机的理论风速-风功率曲线(图 1)。从图 1中可以看出, Ⅰ期风机切入风速为3.5 m·s-1, 额定风速为12.5 m·s-1, 其切断风速为25 m·s-1, 额定功率输出为2 000 kW; Ⅱ期风机切入风速为3.5 m·s-1, 额定风速为11 m·s-1, 其切断风速为25 m·s-1, 额定功率输出为1 500 kW。由此获取特定时段内风机发电量。
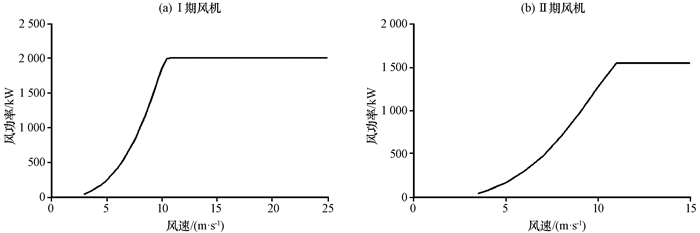
|
图 1 Ⅰ期和Ⅱ期风机的理论风速-风功率曲线 Figure 1 Wind speed-power curve of different wind turbine types in the study area |
(2) 考虑传输损耗时, 一般利用容量因子CP描述风机发电效率(Torres et al, 2003)。CP如果较高, 则表明该电场发电成本显著降低, 经济效益相应提高(Marčiukaitisa et al, 2015)。
| $ {C_p} = \frac{{{P_{{\rm{fact}}}}}}{{{P_{{\rm{pot}}}}}} \times 100\% , $ | (12) |
式中: Cp为发电量容量因子; Pfact为发电期实际发电量(单位: kW·h); Ppot为相同发电期内的潜在发电量(单位: kW·h), 如果风机按最大装机容量运行, 则可能在同时期产生实际发电量等于潜在发电量的情况。
(3) 考虑控制策略影响时(如弃风限电现象), 还需要利用弃风率η分析风机的发电损失(国家电监会, 2013)。
| $ \eta = \frac{{{P_{\max }} - {P_{{\rm{fact}}}}}}{{{P_{\max }}}} \times 100\% , $ | (13) |
式中: Pmax为潜在最大发电量(单位: kW·h); Pmax-Pfact为风电场弃风电量(单位: kW·h)。获取潜在最大发电量时, 需要将实际风速代入通过理论风速-风功率曲线计算风功率, 进而获取特定时间段内的实际发电量。Pmax计算过程中不考虑风机损耗, 且假定理论风速-风功率曲线固定不变。
基于上述, 初步形成一个可用于复杂地形下的微尺度风电场风电功率预报集成建模框架(图 2)。具体包括: (1)定量分析BJ-RUC模式和SCADA数据集, 并建立CFD和Kalman滤波集成建模方法; (2)分析研究区风速时空分布特征, 确定CFD边界条件, 模拟风速场分布并获得风速分区预处理场; (3)根据BJ-RUC和SCADA数据获得Kalman滤波递推的初始参数, 完成集成模型模拟和分析; (4)检验风电场预测风功率和评估发电效益, 并做不确定性分析。
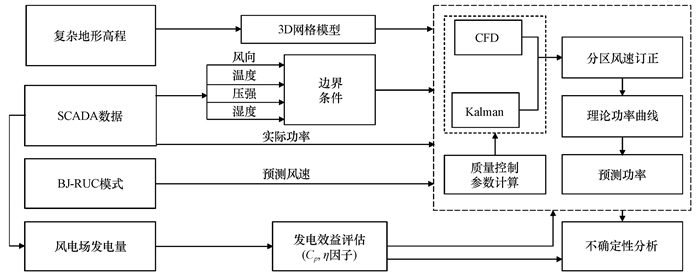
|
图 2 风电场风电功率预报集成建模框架 Figure 2 An integrated modeling framework of wind power for forecast in the study area |
基于已有的SCADA和BJ-RUC数据, 分别获取风电场2014年全年的观测与预报资料, 并绘制风向-风速-风频玫瑰图(图 3), 其中风频指的是某一风向的次数占总的观测统计次数的百分比。对比发现: (1)南湫风电场的全年主导风向为N; (2)根据风速-风功率曲线(见图 1)将电场58台风机观测数据划分为3个风速区间:低风速区为0~3.5 m·s-1, 风频为37.84%;有效风速区间为3.5~11 m·s-1, 风频为61.16%;满发风速区间为11~25 m·s-1, 风频为1%; (3)电场58台风机预报的数据中, 低风速区间的风频为5%, 有效风速区间的风频为64.06%, 满发风速区间的风频为30.94%, 对比观测值和预报值发现, BJ-RUC模式在有效风速区和满发风速区的风速预报整体偏高。
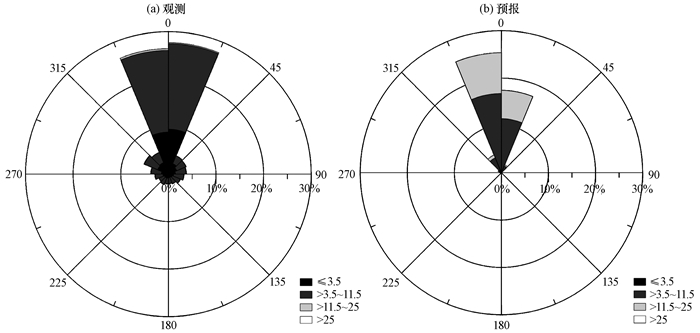
|
图 3 研究区2014年观测(a)与预报(b)风向-风速-风频玫瑰图(单位: m·s-1) Figure 3 The direction and speed of wind rose diagram of the observation (a) and simulation (b) by BJ-RUC in 2014.Unit: m·s-1 |
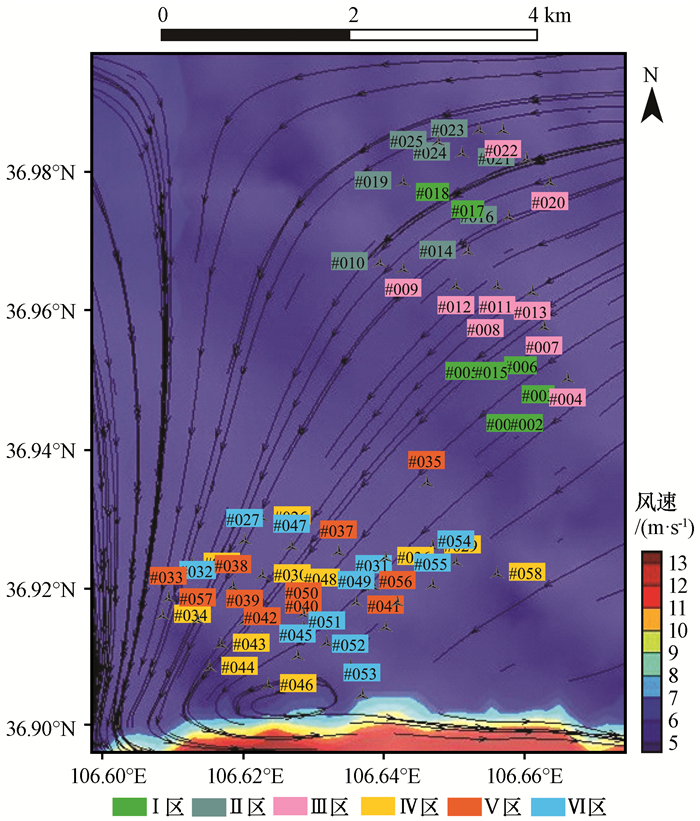
结合地形图, 在ArcGIS 10.2中进一步获取风电场三维高程图与风机分布(图 4)。从图 4中可以看出, #001~#025为Ⅰ期风机(每台2 000 kW), #026~#058为Ⅱ期风机(每台1 500 kW)。从地形分布看, 风速因山区地形起伏差异较大, 其地形像一个倾斜的“马蹄”; 还发现在36.94°N-36.98°N、106.6°E-106.63°E之间有一个斜三角山谷, 围绕该山谷边缘的风机风速明显低于山顶风机的风速, 这也是造成模式低风速区整体预报效果较差的原因。通过对比两期风机数据发现, Ⅰ期风机的风速较小, 这可能与南湫风电场特殊的微尺度地形分布和黄土高原沟壑区地理位置密切相关。针对复杂地形下出现的风速差异现象, 需要在风能预报过程中进一步划分不同风机类型区域和分区预报。

|
图 4 研究区风机分布 Figure 4 Distribution map of wind turbines in the study area |
南湫风电场海拔范围为1 650~2 060 m, 受“马蹄”型地形等因素影响, 全年风速变化较大。分析58台风机的全年SCADA数据发现, 2014年6月19日15:00(北京时, 下同)出现最大风力。其中, #051风机出现最大风速, 为26.84 m·s-1, 已超过额定风速; #047风机出现最小风速, 为12.25 m·s-1, 已达到满发风速标准; 风电场内不同区域的风机风速相差最大达14.59 m·s-1。表明传统预报方法无法考虑地形内部的风速差异及极端大风天气的影响, 且传统预报一般将全场风机风速加权平均之后再进行功率预报, 导致风速和风功率预报误差加大。通过CFD建模能精细化地模拟风场内部地形要素影响及细微的风场变化。基于CFD建模结果, 可以对南湫风电场进行精确的风速区划分, 提高后期的风速和风功率预报精度。
根据研究区高程与风速变化选取CFD边界条件, 将z0设为1 600 m, 将v0设为20 m·s-1, 风速入口方向为北向(0°); 根据大气稳定度标准(GB/T13201-91)(国家技术监督局和国家环境保护局, 1992), 取P=0.33。基于CFD完成南湫风电场风速分布模拟(图 5), #001~#025为Ⅰ期风机(每台2000 kW), #026~#058为Ⅱ期风机(每台1 500 kW), 将风电场的两期风机区域按CFD模拟风速值的大小依次排序, 共分为6个子区域(表 1)。
|
图 5 研究区CFD模拟的风速场分布 Figure 5 The distribution of wind speed field by CFD in the study area |
| 表 1 研究区6个风区内模拟的风速值 Table 1 The simulated wind speed of 6 wind zones in the study area |
(1) Ⅰ期风电场包括Ⅰ—Ⅲ区, Ⅰ区以#005风机为代表, 风速为5.77 m·s-1, 该区处于Ⅰ期边缘处, 最靠近山谷东部边缘, 受复杂地形影响最大, 是风速最小的区域; Ⅱ区以#024风机为代表, 风速为6.21 m·s-1, 其风速仅高于Ⅰ区, 靠近山谷北部边缘, 风速受地形影响, 有一定程度的减弱; Ⅲ区以#012风机为代表, 风速为6.72 m·s-1, 分区风速最大, 位于“马蹄形”山区顶部, 是Ⅰ期3个子区域中受地形影响最小区域。
(2) Ⅱ期风电场包括Ⅳ—Ⅵ区, 风速分布情况较复杂。其中, Ⅳ区以#046风机为代表, 风速为5.86 m·s-1, 在#046周围形成明显的局地涡流, 该区靠近山谷南部边缘, 位于“马蹄形”山梁南部的两侧, 受复杂地形及局地涡流的顺时针来向风的影响最大, 是Ⅱ期中风速最小的子区域; Ⅴ区以#056风机为代表, 风速为6.40 m·s-1, 其风速仅高于Ⅳ区, 处于山谷南部边缘山梁的更高处, 局地涡流的顺时针来向风对风速有一定影响, 但相比Ⅳ区有所减弱; Ⅵ区以#031风机为代表, 风速为6.94 m·s-1, 此分区风速最大, 位于远离局地涡流的山区与局地涡流的背风区, 是受地形和局地涡流影响最小的区域。
3.3 基于Kalman滤波的分区风速订正对BJ-RUC中内嵌的数值预报模式WRF(The Weather Research and Forecasting Model)的气象场输出数据进行降尺度和插值, 使预报产品格点分辨率由9 km×9 km提高至3 km×3 km, 并进一步利用CALMET动力降尺度模式将气象场分辨率提高到1 km×1 km, 再插值到各风机的轮毂高度, 并输出风机未来72 h的15 min时间格点的风速和风向等气象要素资料。该产品虽然包含了地形对风速的影响, 但实际应用效果并不理想(图 3), 为更好地提高其风场预报效果, 应用Kalman滤波订正分区风速。
(1) 获取Kalman滤波递推的初始值。分析统计2014年6月1-15日6个子风区中代表性风机(#005, #012, #024, #031, #046, #056)的预报风速、实况功率与观测资料, 获取参数
| $ {{\hat \beta }_0} = {\left[ {2.393;0.018;0.008} \right]^T}, $ | (14) |
| $ W = \left[ {\begin{array}{*{20}{c}} {6.268413652093253e - 5}&0&0\\ 0&{2.837968100694412e - 8}&0\\ 0&0&{1.875442746034007e - 10} \end{array}} \right], $ | (15) |
式中: V为量测噪声方差阵, 由于预报量只有一个分量, 因此V=1.411;设C0为零矩阵。
(2) Kalman滤波订正。根据递推初始参数
| 表 2 不同风区初始预报与订正后的风速准确率对比 Table 2 Comparison of forecast error between corrected and initial wind speed in the 6 wind zones |
由表 2知, 经过Kalman滤波订正后的各风区预报效果均有明显改善, 总体预报准确率达到90%以上。对比各风区发现, 校订后的Ⅰ区预报准确率为91.5%, 仍为风速准确率最低风区, 这可能是由于Ⅰ区靠近山谷东部边缘, 受复杂的黄土高原沟壑区地形影响最大, 该区预报难度较大; 除Ⅰ区外, 其余分区预报效果较好; 还发现两期风场中的中等风速区(Ⅱ区和Ⅳ区)经Kalman滤波订正后准确率提高最显著, 分别提高了73.40%和68.50%。
分别分析6个风区中6台代表性风机的风速变化曲线(图 6)。从图 6中可以看出, Kalman滤波订正后的风机平均风速与观测平均风速较接近, 最大绝对误差均小于2 m·s-1, 表明风速分区预报产生了较好的预报效果, 提高了风速预报准确率。上述分析也表明, BJ-RUC模式在微尺度复杂地形的风电场应用方面并不理想, 风速预报准确率普遍较低, 集成CFD分区建模和Kalman滤波订正的方法弥补了BJ-RUC模拟的缺陷。
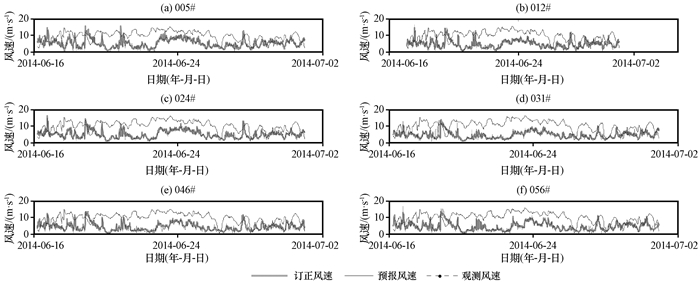
|
图 6 不同风机的BJ-RUC预报与Kalman订正风速的比较 Figure 6 The comparison of BJ-RUC and Kalman filter of wind speed for different wind turbines |
风电场风功率计算的通用方法是物理法, 即将预报风速分别代入电场Ⅰ期和Ⅱ期的理论功率曲线, 以此实现风功率预报。具体采用分段线性回归计算方法, 并开发长时间序列的数据迭代计算方法, 通过Matlab12.0编程完成。在风速订正基础上, 应用上述算法获取2014年6月16-31日实时预报风功率, 并与风电场的实况风功率进行对比分析(图 7)发现, Kalman滤波订正后的预报风功率精度明显得到改善。针对国家电网和甘肃省电力调度中心的风功率准确率考核需求, 进一步计算两期风功率预报准确率(表 3)。从表 3中可以发现, Ⅰ期和Ⅱ期风功率预报准确率均达80%以上, 预报功率与实况功率的相关系数均大于0.85, 表明分区预报方法有助于提高风电场的风功率准确率。由图 7可知, 6月16日和19日两天的电场发电功率曲线出现波峰值, 分别达到5×104 kW和6×104 kW。在风速较大且发电量猛增情况下, 实况风功率明显低于预测风功率, 但同期风速预报准确率则较高, 误差小于2 m·s-1, 需要进一步分析风电场实况发电能力和评估发电效益。
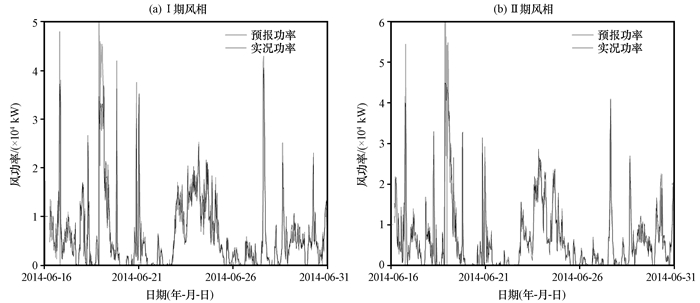
|
图 7 Ⅰ期和Ⅱ期的预报风功率与实况风功率对比 Figure 7 The comparison of wind power for forecast and observation in different regions |
| 表 3 Ⅰ期和Ⅱ期的功率预测预报准确率 Table 3 The forecast error comparison in different regions |
根据验证期内各风机累积发电量, 利用ArcGIS 10.2空间地统计模块的普通克里金插值法, 获取风电场实际累积发电量空间分布[图 8(a)]。对比风速空间分布和地形发现, 发电量与风速的空间变化趋势较一致, 受地形和局地涡流的影响较大, 风电场实际累积发电量在高海拔山顶及涡流顺时针方向具有较高值, 如Ⅰ期的#004风机累积发电量高达4.6×105 kW·h。从图 8(b)中可以看出, Ⅰ期和Ⅱ期的发电量容量因子CP变化趋势基本一致, 但Ⅱ期CP值普遍较高; Ⅱ期电力容量在6月19日出现最大波峰值, 达到100%, 表明该期间电场发电能力较强, Ⅰ期虽然同期也在波峰阶段, CP仅为70.57%; CP与风速变化和功率变化曲线趋势较一致, 表现出较强相关性, 表明风电场发电能力同样受地形和局地涡流影响。
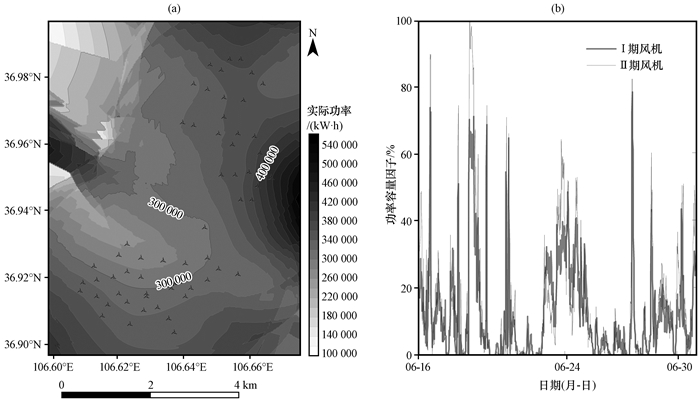
|
图 8 实际发电量(a)和两期风电场的容量因子(b)随时间演变 Figure 8 The temporal evolution of actual production (a) and capacity factor (b) in different regions |
CP值的大小取决于风电场的装机容量, 当装机容量较大时CP值高, 当风力发电机分散在更广泛的区域时, 获得风能的可能性会更大(Iglesias et al, 2010)。获取发电效益评估因子的空间分布, 在ArcGIS 10.2中利用空间地统计模块分别对CP和η进行空间插值, 插值方法仍为普通克里金插值法, 获取风电场CP和η空间分布。从图 9(a)中可以看出, 在Ⅰ期和Ⅱ期装机容量相差不明显的情况下, Ⅱ期装机台数达34台, 远高于Ⅰ期的24台, Ⅰ期平均CP值为12.13%, Ⅱ期平均CP值为14.40%。结合各子风区风速分布发现, Ⅱ期各风速区的风速普遍高于Ⅰ期, 说明Ⅱ期相比Ⅰ期的发电经济效益较强。弃风率η表现出不同的空间分布特征[图 9(b)]。Ⅰ期和Ⅱ期的整体弃风率η分别达10.1%和13.5%, 该风电场有明显弃风现象, 这也解释了其实况功率和发电量偏低的现象; 同时, Ⅱ期整体弃风率η高于Ⅰ期, 表明发电能力较强区域出现了更明显的弃风现象, 这与地方电力管理部门和电厂本身运营能力相关, 在实际决策中要权衡分析。
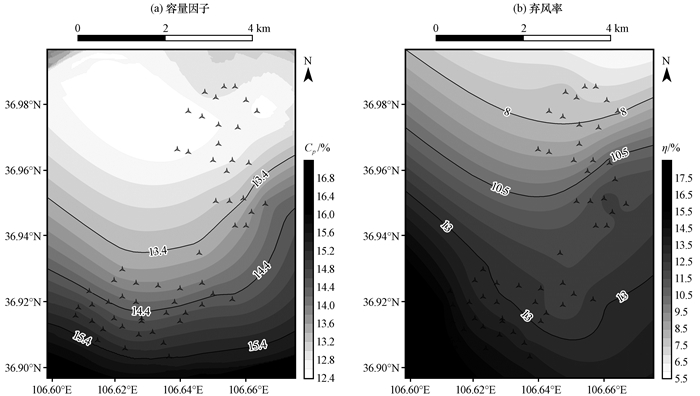
|
图 9 容量因子(a)和弃风率(b)空间分布 Figure 9 Spatial distribution of capacity factor (a) and curtailment rate (b) |
在集成BJ-RUC模拟、CFD模拟与Kalman滤波的基础上, 使用标准理论功率曲线计算风机功率输出和评估发电效益, 初步构建了一个可用于微尺度复杂地形区风速-风功率预测的集成建模框架和方法。建模方法仍存在不确定性。首先, SCADA系统的数据精度、完整性和合理性问题会对集成建模产生不确定性影响, 需要在业务系统中设置数据传输中断的报警、数据补传或替代功能, 进一步加强数据质量评估和检验; 其次, Kalman滤波订正结果的长时间序列验证存在困难, 不同时段的验证数据可能会导致模型精度存在不一致性, 风场未来状态及风机可能发生的故障等均存在不确定性, 需要深入进行多情景的数据验证及对比分析; 第三, 黄土高原沟壑区的微尺度地形十分复杂, BJ-RUC产品无法完全满足风场局地尺度的动力特性, 需要检验降尺度的格网分辨率的合理性, 沟壑地形导致的复杂环流现象也对CFD风场模拟方法提出了更高要求(刘丽珺等, 2013);最后, 本研究使用的标准理论功率曲线并不能完全代表电场实际发电能力, 这与电场发电效益要求、能源管理部门决策和新能源产业发展环境等因素密切关系, 需要进一步考虑上述因子影响, 并综合权衡。
在集成建模方法中, CFD模拟主要用于产生风电场的风速分区预处理场, 未参与后期基于Kalman滤波的风速动态订正计算, 今后在计算条件允许的情况下将进一步基于CFD进行风速分区预处理场的实时更新; SCADA系统主要用于获取风速、风功率等风机实时数据, 为Kalman滤波提供各个风速分区的样本训练数据; Kalman滤波算法较成熟, 可以利用计算机程序实现自动运行, 耗时短。总体看, 本文提出的集成建模方法优化了研究区风速-风功率预报精度, 形成了可用的风速-风功率订正与预报建模框架。今后会进一步加强多模型耦合研究, 实现数据和模型机理完全耦合的系统开发, 并探索类似微尺度复杂地形区风速-风功率系统业务化运行的可能性和可移植性。研究的主要结论有:
(1) CFD能精确地重现微尺度复杂地形对湍流的影响, 能再现尾流相互作用及其与风速分布关系的地形物理效应, 弥补了BJ-RUC网格粗糙的问题。模拟发现风资源集中在“马蹄”型山区顶部, 受地形影响小, 风速大; 风机最大风速差值为2.78 m·s-1, 风机风速变化同其地形复杂程度一致。
(2) Kalman滤波能有效地实现对BJ-RUC产品的快速订正与预测。通过提取和订正CFD模拟产生的风速分区样本数据, 显著地提高了风电场的风速预测精度, 整体准确率达90%以上。
(3) 通过风功率预测检验、发电能力分析和效益评估发现, 集成建模方法使风电场的风功率预测精度均达到80%以上。CP和η变化表明该电场的风功率和发电量预测能力均受发电能力限制, CP既受地形、局地涡流、电场装机容量与风机台数等因素影响; η与电场设备、运营情况及当地能源部门决策等因素相关; 开发能集成新能源行业相关动态因素的风能预测方法会对未来新能源发展产生重要意义。
致谢 感谢中国华电集团福新能源股份有限公司甘肃分公司提供SCADA数据。
Addison J F D, Hunter A, Bass J, et al, 2000. A neural network version of the measure correlate predict algorithm for estimating wind energy yield[J]. G730 Neural Computing.
|
|
Benjamin S G, Dévényi D, Weygandt S S, et al. 2004. An hourly assimilation-forecast cycle:The RUC[J]. Mon Wea Rev, 132(2): 495–518.
DOI:10.1175/1520-0493(2004)132<0495:AHACTR>2.0.CO;2 |
|
Cassola F, Burlando M. 2012. Wind speed and wind energy forecast through Kalman filtering of numerical weather prediction model output[J]. Appl Energy, 99: 154–166.
DOI:10.1016/j.apenergy.2012.03.054 |
|
Castellani F, Burlando M, Taghizadeh S, et al. 2014. Wind energy forecast in complex sites with a hybrid neural network and CFD based method[J]. Energy Procedia, 45: 188–197.
DOI:10.1016/j.egypro.2014.01.021 |
|
Counehan J. 1971. Wind tunnel determination of the roughness length as a function of the fetch and the roughness density of three-dimensional roughness elements[J]. Atmos Environ, 5(8): 637–642.
DOI:10.1016/0004-6981(71)90120-X |
|
Doucoure B, Agbossou K, Cardenas A. 2016. Time series prediction using artificial wavelet neural network and multi-resolution analysis:Application to wind speed data[J]. Renewable Energy, 92: 202–211.
DOI:10.1016/j.renene.2016.02.003 |
|
Foley A M, Leahy P G, Marvuglia A, et al. 2012. Current methods and advances in forecasting of wind power generation[J]. Renewable Energy, 37(1): 1–8.
DOI:10.1016/j.renene.2011.05.033 |
|
Iglesias G, Castellanos P, Seijas A. 2010. Measurement of productive efficiency with frontier methods:A case study for wind farms[J]. Energy Economics, 32(5): 1199–1208.
DOI:10.1016/j.eneco.2010.03.004 |
|
Johnson G L, 2006. Wind energy systems[M]. Gary L. Johnson.
|
|
Kusiak A, Li W. 2011. The prediction and diagnosis of wind turbine faults[J]. Renewable Energy, 36(1): 16–23.
DOI:10.1016/j.renene.2010.05.014 |
|
Kusiak A, Verma A. 2013. Monitoring wind farms with performance curves[J]. IEEE Trans Sustain Energy, 4(1): 192–199.
DOI:10.1109/TSTE.2012.2212470 |
|
Landberg L. 2001. Short-term prediction of local wind conditions[J]. Journal of Wind Engineering and Industrial Aerodynamics, 89(3): 235–245.
DOI:10.1007/BF00712528 |
|
Launder B E, Spalding D B. 1974. The numerical computation of turbulent flows[J]. Computer Methods In Applied Mechanics And Engineering, 3(2): 269–289.
DOI:10.1016/0045-7825(74)90029-2 |
|
Liu S, Pan W, Zhang H, et al. 2017. CFD simulations of wind distribution in an urban community with a full-scale geometrical model[J]. Building and Environment, 117: 11–23.
DOI:10.1016/j.buildenv.2017.02.021 |
|
Louka P, Galanis G, Siebert N, et al. 2008. Improvements in wind speed forecasts for wind power prediction purposes using Kalman filtering[J]. Journal of Wind Engineering and Industrial Aerodynamics, 96(12): 2348–2362.
DOI:10.1016/j.jweia.2008.03.013 |
|
Lundtang P E, Mortensen N G, Landberg L, et al, 1997. Wind power meteorology[R]. Risø National Laboratory.
|
|
Magnusson M, Wern L, 2001. PG1. 54 Wind energy predictions using CFD and HIRLAM forecasts[C]//EWEC-CONFERENCE. 861-863.
|
|
Marčiukaitisa M, Katinas V, Geceviius G, 2015. Analysis of economic, environment, social factors and efficiency of wind turbines in Lithuania[C]//Trends and challenges for wind energy harvesting: workshop, March 30-31, Coimbra, Portugal.
|
|
Schlechtingen M, Santos I F, Achiche S. 2013. Wind turbine condition monitoring based on SCADA data using normal behavior models.Part 1:System description[J]. Applied Soft Computing, 13(1): 259–270.
DOI:10.1016/j.asoc.2012.08.033 |
|
Song M X, Chen K, Zhang X, et al. 2015. The lazy greedy algorithm for power optimization of wind turbine positioning on complex terrain[J]. Energy, 80: 567–574.
DOI:10.1016/j.energy.2014.12.012 |
|
Torres J L, Prieto E, Garcia A, et al. 2003. Effects of the model selected for the power curve on the site effectiveness and the capacity factor of a pitch regulated wind turbine[J]. Solar Energy, 74(2): 93–102.
DOI:10.1016/S0038-092X(03)00144-0 |
|
Yang W, Court R, Jiang J. 2013. Wind turbine condition monitoring by the approach of SCADA data analysis[J]. Renewable Energy, 53: 365–376.
DOI:10.1016/j.renene.2012.11.030 |
|
陈正洪. 2013. 风电功率预测预报技术原理及其业务系统[M]. 北京: 气象出版社.
Chen Z H. 2013. The principle of wind power forecasting and forecasting technology and its operational system[M]. Beijing: China meteorological press.
|
|
程兴宏, 陶树旺, 魏磊, 等. 2012. 基于WRF模式和自适应偏最小二乘回归法的风能预报试验研究[J]. 高原气象, 31(5): 1461–1469.
Cheng X H, Tao S W, Wei L, et al. 2012. Short-term wind power forecasting experiment based on WRF Model and adapting partial least square regression method[J]. Plateau Meteor, 31(5): 1461–1469.
|
|
丁煌, 陶树旺, 肖子牛, 等. 2013. 基于WRF和SVM方法的风电场功率预报技术研究[J]. 高原气象, 32(2): 581–587.
Ding H, Tao S W, Xiao Z N, et al. 2013. Study on wind power forecasting of wind farm based on WRF and SVM[J]. Plateau Meteor, 32(2): 581–587.
DOI:10.7522/j.issn.1000-0534.2012.00056 |
|
国家电监会, 2013. 风电场弃风电量计算办法(试行)[S].
State Electricity Regulatory Commission, 2013. Wind power calculation method for wind farm (Trial)[S].
|
|
国家技术监督局, 国家环境保护局, 1992. GB/T 3840-1991制定地方大气污染物排放标准的技术方法[S].
State Bureau of Technology Supervision, State Environmental Protection Administration, 1992. GB/T 3840-1991 Technical methods for making local emission standards of air pollutants[S].
|
|
国家能源局, 2014. NB/T 31046-2013风电功率预测系统功能规范[S].
National Energy Administration, 2014. NB/T 31046-2013 Function specification of wind power forecasting system[S].
|
|
国家能源局. 2016. 2016年一季度风电并网运行情况[J]. 中国能源, 38(5): 33–33.
National Energy Administration. 2016. Wind power grid operation in the first quarter of 2016[J]. Energy of China, 38(5): 33–33.
|
|
国家能源局. 2017. 2016年风电消纳情况公布[J]. 风能, 4: 8.
National Energy Administration. 2017. Announcement of wind power consumption in 2016[J]. Wind energy, 4: 8.
|
|
国家质检总局, 2002. GB/T 18710-2002风电场风能资源评估方法[S].
General Administration of Quality Supervision, 2002. GB/T 18710-2002 Methodology of wind energy resource assessment for wind farm[S].
|
|
李芬, 陈正洪, 蔡涛, 等. 2013. 并网光伏系统性能精细化评估方法研究[J]. 太阳能学报, 34(6): 974–983.
Li F, Chen Z H, Cai T, et al. 2013. Refinement assessment method of grid-connected PV system performance[J]. Acta Energiae Solaris Sinica, 34(6): 974–983.
|
|
刘丽珺, 梁友嘉. 2016. BJ-RUC模式的低层风场预报产品质量检验——以甘肃省当金山风电场为例[J]. 干旱气象, 34(4): 743–751.
Liu L J, Liang Y J. 2016. Quality assessment of low-level wind prediction product by BJ-RUC Model-A case study of akesai wind farm in Gansu Province[J]. J Arid Meteor, 34(4): 743–751.
DOI:10.11755/j.issn.1006-7639(2016)-04-0743 |
|
刘丽珺, 吕萍, 梁友嘉. 2013. 基于CFD技术的河谷型城市风环境模拟——以兰州市城关区为例[J]. 中国沙漠, 33(6): 1840–1847.
Liu L J, Lv P, Liang Y J. 2013. Simulating wind environment of valley city based CFD technology:A case study of Chengguan District of Lanzhou, China[J]. J Desert Res, 33(6): 1840–1847.
DOI:10.7522/j.issn.1000-694X.2013.00244 |
|
柳艳香, 陶树旺, 张秀芝. 2008. 风能预报方法研究进展[J]. 气候变化研究进展, 4(4): 209–214.
Liu Y X, Tao S W, Zhang X Z. 2008. Review on methods of wind power forecasting[J]. Climate Change Res, 4(4): 209–214.
|
|
陆如华, 徐传玉, 张玲, 等. 1997. Kalman滤波的初值计算方法及其应用[J]. 应用气象学报, 8(1): 34–43.
Lu R H, Xu C Y, Zhang L, et al. 1997. Initial value calculation method of Kalman filter and its application[J]. Quart J Appl Meteor, 8(1): 34–43.
|
|
石岚, 徐丽娜, 郝玉珠. 2017. 多模式风速融合预报应用研究[J]. 高原气象, 36(4): 1022–1028.
Shi L, Xu L N, Hao Y Z. 2017. Application research on the Multi-Model fusion forecast of wind speed[J]. Plateau Meteor, 36(4): 1022–1028.
DOI:10.7522/j.issn.1000-0534.2017.00021 |
|
王澄海, 胡菊, 靳双龙, 等. 2011. 中尺度WRF模式在西北西部地区低层风场模拟中的应用和检验[J]. 干旱气象, 29(2): 161–167.
Wang C H, Hu J, Jin S L, et al. 2011. Application and test of lower level wind field simulation with meso-scale WRF in western region of Northwest China[J]. J Arid Meteor, 29(2): 161–167.
|
|
王丹云, 吕世华, 韩博, 等. 2017. 近30年黄土高原春季降水特征与春旱变化的关系[J]. 高原气象, 36(2): 395–406.
Wang D Y, Lv S H, Han B, et al. 2017. Characteristics of spring precipitation and their connections with the spring drought over the Loess Plateau during last three decades[J]. Plateau Meteor, 36(2): 395–406.
DOI:10.7522/j.issn.1000-0534.2016.00121 |
|
魏东, 尤凤春, 范水勇, 等. 2010. 北京快速更新循环预报系统(BJ-RUC)模式探空质量评估分析[J]. 气象, 36(8): 72–80.
Wei D, You F C, Fan S Y, et al. 2010. Analysis of radial quality evaluation of Beijing rapid renewal circulation forecasting system (BJ-RUC) Model[J]. Meteor Mon, 36(8): 72–80.
DOI:10.7519/j.issn.1000-0526.2011.12.003 |
|
张双益, 胡非. 2017. 大气边界层与风力发电的相互作用研究综述[J]. 高原气象, 36(4): 1127–1137.
Zhang S Y, Hu F. 2017. Review on study of atmospheric boundary layer and wind power generation interaction[J]. Plateau Meteor, 36(4): 1127–1137.
DOI:10.7522/j.issn.1000-0534.2016.00095 |
|
张新科, 陈晋北, 余晔, 等. 2017. 雷暴系统影响下的黄土高原塬区微气象特征研究[J]. 高原气象, 36(2): 384–394.
Zhang X K, Chen J B, Yu Y, et al. 2017. Study on the micrometeorological characteristics over the Loess Plateau under the influence of thunderstorm[J]. Plateau Meteor, 36(2): 384–394.
DOI:10.7522/j.issn.1000-0534.2017.00002 |
|
祝赢, 柳艳香, 严金蓉, 等, 2012. 基于卡尔曼滤波的模式预报风速订正方法研究[C]//全国环境风工程学术会议.
Zhu Y, Liu Y X, Yan J R, et al, 2012. Study on model prediction wind speed correction method based on Calman filtering[C]//National Conference on environmental wind engineering.
|
2. Hubei Key Laboratory of Inland Shipping Technology, Wuhan 430063, Hubei, China;
3. National Engineering Research Center for Water Transport Safety, Wuhan 430063, Hubei, China;
4. School of Resources and Environmental Engineering, Wuhan 430070, Hubei, China
 2018, Vol. 37
2018, Vol. 37
