1 引言

工农业生产及人民生活对系统供电的稳定性和可靠性要求越来越高, 雷电则是威胁输电线路安全的重要因素, 已有研究表明, 感应雷过电压引发线路故障的比率已经超过90%, 成为输电中断的主要原因(代杰杰等, 2016;刘晓东等, 2014;许霖等, 2017;刘妍秀等, 2016)。输电线路防雷设计和实施以感应过电压特征研究为前提(边凯等, 2013), 对于传输线雷电感应电压的计算, 国内外学者多采用两步递进方式实现, 首先求解雷电回击通道产生的电磁场, 然后利用场-线耦合模型求解电磁场在线路上的感应电压(章涵等, 2012;边凯等, 2012;张其林等, 2003)。

Sommerfeld(1909)利用数值积分法, 提出了计算雷电电磁场的经典公式, Cooray(2002)和Rubinstein(1996)对方法进行改善并利用其分析回击参数对雷电电磁场的影响。随着高性能计算机的发展, FDTD(Finite-Difference Time-Domain)成为计算雷电电磁场的常用方法, Yang et al(2004)利用该方法得到的垂直电场与实验结果高度一致, Baba et al(2009)计算不同距离处的磁场结果与观测实验结果同样具有较好的一致性。

在计算雷电电磁脉冲与传输线耦合作用时, 根据不同激励源有三种常用模型(Agrawal et al, 1980; Taylor et al, 1987; Rachidi, 1993), 其中Agrawal耦合模型的准确性已经被人工引雷实验所验证(Barker et al, 1996)。此外, 为了快速估算架空传输线雷电感应过电压量纲, Paulino et al(2011)推到了线路中点位置感应电压的近似公式, 也有学者针对我国标准中规程公式进行分析和改进(高金阁等, 2017)。近似算法只能估算线路中点总电压的量纲, 无法对线路其他位置、电压分量等进行分析研究。

目前, 雷电感应过电压研究成果多以传播介质为理想导体为前提, 然而雷电电磁脉冲受地表电参数影响较大(Cooray, 1994), 势必影响传输线雷电感应电压分析的准确性。因此, 通过建立回击通道和传输线一体化数值计算模型, 实现利用FDTD方法求解雷电感应过电压, 并与已有文献对比验证方法的有效性。研究传输线不同位置感应电压特征及电压分量对总电压的贡献, 进而分析均匀有限电导率地表对传输线中点和端点处感应电压的影响。研究成果为合理设计、实施架空线路雷电防护提高参考。

2 FDTD雷电感应电压算法介绍 2.1 时域Agrawal耦合模型

在Agrawal耦合模型中, 雷电回击通道附近传输线上的感应过电压由散射电压和入射电压两部分组成, 其表达式为:

$ \begin{array}{l} V\left( {x,t} \right) = {V^s}\left( {x,t} \right) + {V^e}\left( {x,t} \right)\\ \;\;\;\;\;\;\;\;\;\;\; = {V^s}\left( {x,t} \right) - \int_0^h {E_z^e\left( {x,z} \right){\rm{d}}z} , \end{array} $

(1)

式中: V^e为入射电压, 是雷电电场脉冲垂直电场分量在导体高度处的电位; V^s为散射电压, 其与感应电流满足Agrawal模型传输线电报方程。对频域范围的Agrawal电报方程进行傅里叶逆变换得到时域公式为:

$ \frac{{\partial {V^s}\left( {x,t} \right)}}{{\partial x}} + L' \cdot \frac{{\partial I\left( {x,t} \right)}}{{\partial t}} = E_x^e\left( {x,h,t} \right), $

(2)

$ \frac{{\partial I\left( {x,t} \right)}}{{\partial t}} + C' \cdot \frac{{\partial {V^s}\left( {x,t} \right)}}{{\partial t}} = 0, $

(3)

式中: I为流过该点的感应电流; E_x^e为雷电电场脉冲水平电场分量; L′和C′分别为理想传输线单位长度的分布电感和分布电容。将时域Agrawal耦合模型离散后得到感应电压和感应电流的FDTD形式为:

$ \begin{array}{l} {V^s}\left( {k,n + 1} \right) = {V^s}\left( {k,n} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - \frac{{\Delta t}}{{C'}} \cdot \frac{{I\left( {k,n} \right) - I\left( {k - 1,n} \right)}}{{\Delta x}}, \end{array} $

(4)

$ \begin{array}{l} I\left( {k,n + 1} \right) = I\left( {k,n} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - \frac{{\Delta t}}{{L'}} \cdot \frac{{{V^s}\left( {k + 1,n} \right) - {V^s}\left( {k,n} \right)}}{{\Delta x}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - \frac{{E_x^e\left( {k,n + 1} \right) + E_x^e\left( {k,n} \right)}}{2}, \end{array} $

(5)

传输线两端边界条件的差分离散公式为(Orlandi et al, 1996):

$ {V^s}\left( {1,n + 1} \right) = - {R_A} \cdot I\left( {1,n + 1} \right) - {V^e}\left( {1,n + 1} \right), $

(6)

$ \begin{array}{l} {V^s}\left( {n\max ,n + 1} \right) = {R_B} \cdot I\left( {n\max ,n + 1} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - {V^e}\left( {n\max ,n + 1} \right), \end{array} $

(7)

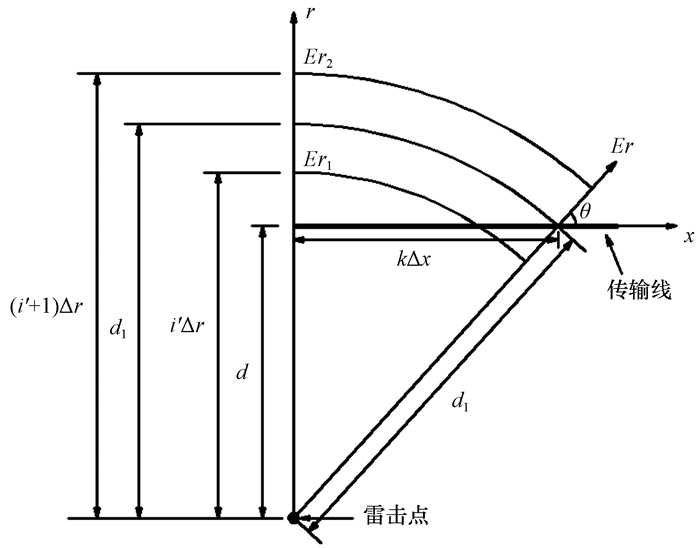
式中: R_A和R_B分别是传输线两端接地阻抗; Δt和Δx分别表示差分的时间步长和空间步长。在利用FDTD求解雷电感应电压时, 作为激励源的电场分量方向必须与传输线切向方向保持一致, 根据图 1所示雷击点与传输线的位置关系, 可以得到激励源电场分量为:

$ {E_x}\left( k \right) = {E_r}\left( {{d_1}} \right) \cdot \cos \theta = {E_r}\left( {{d_1}} \right) \cdot \frac{{k\Delta x}}{{{d_1}}}, $

(8)

式中: E_r(d₁)为距离雷电通道d₁处的水平电场分量, ${d_1} = \sqrt {{d^2} + {{(k\Delta x)}^2}} $, 由于d₁可能不是FDTD计算雷电电磁场的空间取样点, 所以需要对E_r(d₁)进行线性差值处理, 设$ i\prime = {\rm{int}}({d_1}/\Delta r)$, 则:

$ {E_r}\left( {{d_1}} \right) = \left( {1 - \frac{{{d_1} - i'\Delta r}}{{\Delta r}}} \right) \cdot {E_{r1}} + \frac{{{d_1} - i'\Delta r}}{{\Delta r}} \cdot {E_{r2}}. $

(9)

2.2 雷电电磁脉冲FDTD方法求解

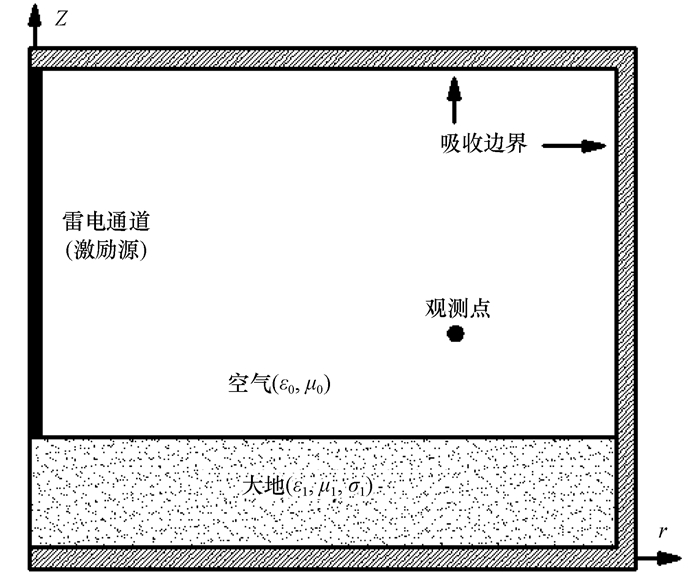
在模拟计算雷电回击通道产生的电磁场时假设通道笔直且垂直于平坦的大地, 忽略通道弯曲的影响, 由此可以得到图 2所示包含雷电通道在内的剖面, 此时电磁场与角度无关。在轴对称二维柱坐标系中, Transverse Magnetic(TM)波的Maxwell方程为:

$ \left\{ \begin{array}{l} \frac{{\partial {E_r}}}{{\partial z}} - \frac{{\partial {E_z}}}{{\partial r}} = - \mu \frac{{\partial {H_\varphi }}}{{\partial t}} - {\sigma _m}{H_\varphi }\\ \frac{{\partial {H_\varphi }}}{{\partial z}} = - \varepsilon \frac{{\partial {E_r}}}{{\partial t}} - \sigma {E_r}\\ \frac{1}{r}\frac{{\partial \left( {r{H_\varphi }} \right)}}{{\partial r}} = \varepsilon \frac{{\partial {E_z}}}{{\partial t}} + \sigma {E_z} \end{array} \right., $

(10)

式中: H_φ、E_r和E_z分别为雷电回击通道在周围产生的磁场、水平电场、垂直电场强度; ε、μ、σ和σ_m分别为介质的介电常数、磁导率、电导率和导磁率, 在自由空间中, σ=σ_m=0, ε=ε₀, μ=μ₀, 对于其他介质ε=ε₀ε_r, μ=μ₀μ_r, 其中: ε_r为介质的相对介电常数; μ_r为介质的相对磁导率。

在FDTD网格中, 电场和磁场分量不仅空间交替抽样, 而且在时间域里也交替取样, 取样时间间隔为半个时间增量, 所以TM波Maxwell方程经离散处理后为:

$ \left\{ \begin{array}{l} H_\varphi ^{n + \frac{1}{2}}\left( {i + \frac{1}{2},j + \frac{1}{2}} \right) = CA \cdot H_\varphi ^{n - \frac{1}{2}}\left( {i + \frac{1}{2},j + \frac{1}{2}} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - CB \cdot \left[ {\frac{{E_r^n\left( {i + \frac{1}{2},j + 1} \right) - E_r^n\left( {i + \frac{1}{2},j} \right)}}{{\Delta z}} - \frac{{E_r^n\left( {i + 1,j + \frac{1}{2}} \right) - E_r^n\left( {i,j + \frac{1}{2}} \right)}}{{\Delta r}}} \right]\\ E_r^{n + \frac{1}{2}}\left( {i + \frac{1}{2},j} \right) = CC \cdot E_r^n\left( {i + \frac{1}{2},j} \right) + CD \cdot \frac{{H_\varphi ^{n + \frac{1}{2}}\left( {i + \frac{1}{2},j + \frac{1}{2}} \right) - H_\varphi ^{n + \frac{1}{2}}\left( {i + \frac{1}{2},j - \frac{1}{2}} \right)}}{{\Delta z}}\\ E_z^{n + 1}\left( {i,j + \frac{1}{2}} \right) = CC \cdot E_z^n\left( {i,j + \frac{1}{2}} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + CD \cdot \frac{{\left( {i + \frac{1}{2}} \right)H_\varphi ^{n + \frac{1}{2}}\left( {i + \frac{1}{2},j + \frac{1}{2}} \right) - \left( {i - \frac{1}{2}} \right)H_\varphi ^{n + \frac{1}{2}}\left( {i - \frac{1}{2},j + \frac{1}{2}} \right)}}{{i\Delta r}} \end{array} \right., $

(11)

式中: $ CA = \frac{{2\mu - {\sigma _m}\Delta t}}{{2\mu + {\sigma _m}\Delta t}};{\rm{ }}CB = \frac{{2\Delta t}}{{(2\mu + {\sigma _m}\Delta t)\Delta z}};{\rm{ }}$ $ CC = \frac{{2\varepsilon - \sigma \Delta t}}{{2\varepsilon + \sigma \Delta t}};{\rm{ }}CD = \frac{{2\Delta t}}{{(2\varepsilon + \sigma \Delta t)\Delta z}}$。

2.3 FDTD的稳定性和吸收边界条件

为确保FDTD方法的准确性, 轴对称柱坐标系中的空间步长和时间步长必须满足Courant稳定性条件(Fusio, 1990), 即:

$ v\Delta t \le \frac{1}{{\sqrt {\frac{1}{{\Delta {r^2}}} + \frac{1}{{\Delta {z^2}}}} }}, $

(12)

式中: v为电磁波在介质中的传播速度; 若Δr=Δz=δ, 则:

$ \Delta t \le \frac{\delta }{{\sqrt 2 \Delta v}}, $

(13)

表明FDTD方法的时间步长的两倍必须小于电磁波沿Yee元胞网格对角线传播所消耗的时间。一阶Mur吸收边界总体虚假反射在1%~5%, 能够较好实现利用有限区域模拟无界空间的目的(Mur, 1981)。在二维柱坐标系中, 回击电流通道作为激励源被设置在图 2左边界上, 其有源吸收边界条件为:

$ \begin{array}{l} E_z^{n + 1}\left( {0,j + \frac{1}{2}} \right) = CC \cdot E_z^n\left( {0,j + \frac{1}{2}} \right) + 4CD\\ \;\;\;\;\;\;\;\; \cdot E_\varphi ^{n + \frac{1}{2}}\left( {\frac{1}{2},j + \frac{1}{2}} \right) - \frac{{4\Delta t}}{{{\rm{ \mathsf{ π} }}{\varepsilon _0}\Delta {r^2}}}I\left( {0,j + \frac{1}{2}} \right), \end{array} $

(14)

式中: I为雷电回击电流元。

3 算法准确性验证 3.1 回击电流模型

雷电流工程模型利用数学表达式描述回击过程相关参量之间的关系, 是计算雷电通道周围电磁场时采用最广泛的回击模型。模拟研究选用改进线性衰减传输线(MTLL)回击模型, 雷电通道高度为7 500 m, 回击电流速度为1.5×10⁸ m·s^-1。回击电流由电晕电流和击穿电流组成, 当回击前沿以速度v到达通道某一高度时, 储存在先导电晕核和电晕鞘的电荷会以不同时间常数被吸收进回击头部, 由于电晕核和电晕鞘的导电性不同, 所以堆积在这两部分内的电荷被回击过程中和的快慢程度不同。模拟时采用双Heidler函数模拟回击通道底部基电流(高金阁等, 2013):

$ \begin{array}{l} I\left( {0,t} \right) = \frac{{{i_{01}}}}{{{\eta _1}}} \cdot \frac{{{{\left( {t/{\tau _{11}}} \right)}^2}}}{{{{\left( {t/{\tau _{11}}} \right)}^2} + 1}} \cdot {e^{ - t/{\tau _{12}}}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\; + \frac{{{i_{02}}}}{{{\eta _2}}} \cdot \frac{{{{\left( {t/{\tau _{21}}} \right)}^2}}}{{{{\left( {t/{\tau _{21}}} \right)}^2} + 1}} \cdot {e^{ - t/{\tau _{22}}}}, \end{array} $

(15)

$ {\eta _1} = \exp \left[ { - \frac{{{\tau _{11}}}}{{{\tau _{21}}}} \cdot {{\left( {2 \times \frac{{{\tau _{12}}}}{{{\tau _{11}}}}} \right)}^{1/2}}} \right], $

(16)

$ {\eta _2} = \exp \left[ { - \frac{{{\tau _{21}}}}{{{\tau _{22}}}} \cdot {{\left( {2 \times \frac{{{\tau _{22}}}}{{{\tau _{21}}}}} \right)}^{1/2}}} \right], $

(17)

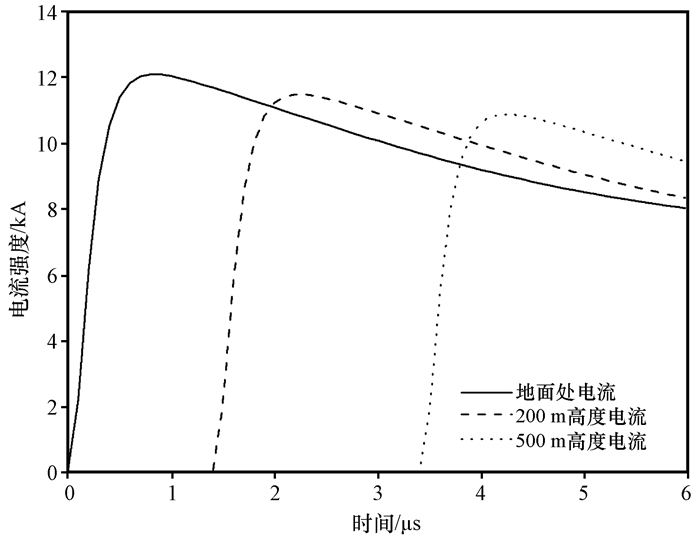
式中: i₀为电晕电流或击穿电流的幅值; τ₁和τ₂分别为电流的上升沿和下降沿时间常数; 具体参数取值为: i₀₁=10.7 kA, τ₁₁=0.25 μs, τ₂₁=2.5 μs, i₀₂=6.5 kA, τ₁₂=2 μs, τ₂₂=230 μs。利用上述参数得到的雷电通道不同高度处回击电流波形图(图 3)可以发现, 通道底部基电流幅值为12 kA, 上升沿时间为0.81 μs, 随着通道内电流点的不断升高, 电流幅值越来越小, 但其上升沿时间并不发生变化。这表明回击通道高度对电流强度有衰减作用, 但并不能够影响回击电流向周围发射的电磁脉冲成分。

3.2 计算结果验证

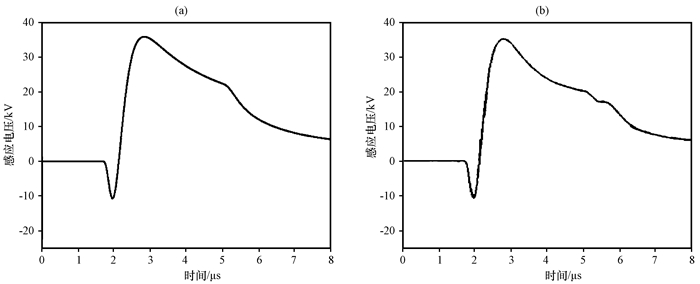
以Agrawal耦合模型为基础, 采用时域有限差分方法(FDTD)计算架空传输线雷电感应过电压。为了验证FDTD计算方法的正确性, 选择的模型参数与Ren et al(2005)保持一致, 即架空传输线高度为10 m, 与雷电通道之间水平距离为50 m, 土壤电导率为0.001 S·m^-1, 传输线长度为1 000 m, 观测点为传输线端点, 时间轴范围为0~8 μs, 电压范围为-25~40 kV。从图 4电压波形对比图可以发现, 两种结果之间不但峰值大小相近, 初始负向峰值为-10 kV左右, 极性反转后的正向峰值为35 kV左右, 而且感应过电压波形也非常相似。Ren et al(2005)的研究结果中感应电压下降出现二次抖动, 可能是由于吸收边界产生反射所致。通过对比可以证明, 模拟使用的2-D FDTD算法具有非常可靠的精度。

4 数值模拟结果分析 4.1 雷电感应过电压分析

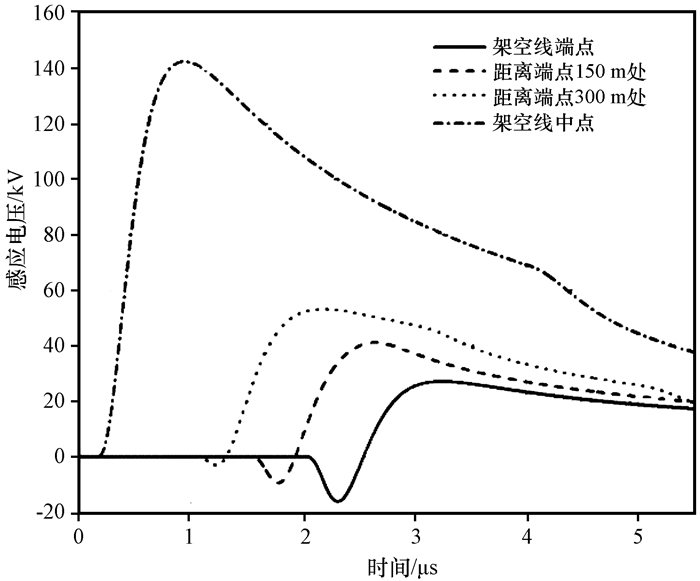
在分析雷电回击电磁场在架空传输线上不同位置耦合产生过电压波形特征时, 设置传输线长度L为1 200 m, 半径a为0.005 m, 终端电阻R为498 Ω, 模拟结果如图 5所示。从图 5中可以发现, 随着测量点从架空线中点向端点移动, 感应过电压的幅值不断减小, 且电压波形的双极性特征越来越明显。电压幅值的减小与路径的衰减作用有关, 随着观测点向端点移动, 回击通道与观测点之间的水平距离增大, 电磁场沿有限电导率介质传播过程中的衰减增大, 使得电磁脉冲中垂直分量不断减小。

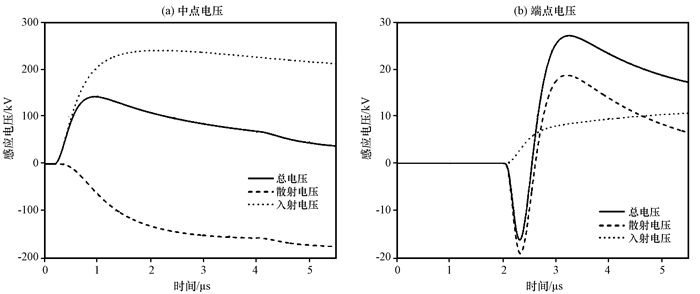
从架空传输线感应总电压及其两个分量之间关系的波形图(图 6)中可以发现, 由水平电场激励产生的散射电压和由垂直电场激励产生的入射电压对架空传输线感应总电压的贡献都较大, 说明雷电电磁脉冲中的水平电场分量和垂直电场分量在耦合机理中都非常重要。值得注意的是, 传输线端点处感应电压双极性特征由散射电压分量决定, 在电磁脉冲到达的开始阶段, 散射电压数值大于入射电压值, 两者极性相反, 使得感应总电压出现负向峰值。

4.2 传输线高度对感应电压的影响分析

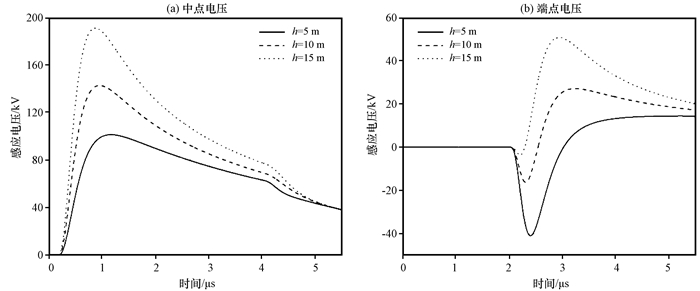
图 7给出了传输线架设高度对感应电压影响的结果, 线高分别设置为h=5, 10和15 m。从图 7中可以发现, 随着传输线高度的增加, 中点感应电压峰值增加, 波头上升沿时间越来越短, 端点电压波形的双极性特征逐渐减弱, 这是因为观测点增高导致散射电压和入射电压增大, 而入射电压随线路高度变化得更加明显, 导致负向峰值随高度增加而减小, 正向峰值随高度增加而增加。因此, 在雷电易发区架设传输线时, 可以采取降低架设高度的方法减少线路受雷电耦合作用发生事故的隐患。

4.3 土壤电导率对感应电压的影响分析

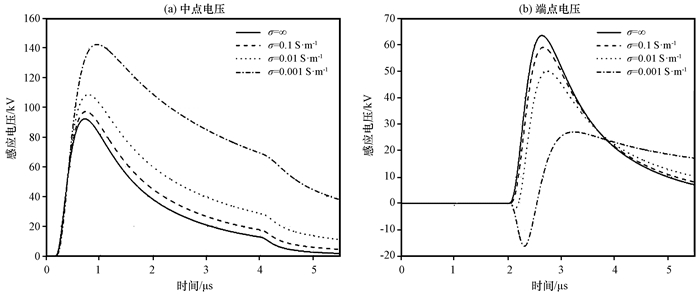
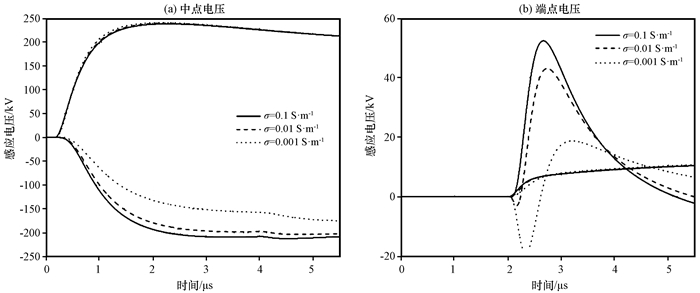
通过均匀有限电导率对雷电感应电压的影响(图 8, 实线表示大地为理想无耗介质, 三条虚线的电导率依次为σ=0.1, 0.01和0.001 S·m^-1)可以发现, 随着土壤电导率减小, 线路中点感应电压峰值越来越大, 并且电导率越小增幅越明显, 所以当架空传输线架设于沙地等低电导率土壤区域时, 工程防护人员应适当提高防护等级, 以防御线路能够承受更大的感应雷过电压[图 8(a)]。当大地电导率从理想无耗情况变为均匀有耗地表时, 端点感应电压波形呈现双极性特征, 这种特征在土壤电导率大于0.1 S·m^-1时并不明显[图 8(b)]。

雷电电磁波在架空传输线上耦合的感应总电压由入射电压和散射电压两部分组成, 为了分析电导率对感应电压产生影响的原因, 对比研究土壤电导率对不同分量产生的影响。从均匀有耗地表对感应电压两个分量的影响结果(图 9)可以发现, 随着土壤电导率的降低, 线路中点的散射电压减小, 端点散射电压初始负向峰值增加, 随后的正向峰值减小, 而线路任何位置处的入射电压变化并不显著。这是因为雷电电场脉冲的水平分量受传播路径的衰减作用影响较大, 而激励产生入射电压的垂直电场分量在几十米范围内受传播路径影响非常有限。

5 结论与讨论

以Agrawal模型电报方程为理论基础, 选取MTLL模型和双Heidler函数作为回击模型和基电流, 建立回击通道和传输线一体化数值计算模型, 利用FDTD方法实现传输线雷电感应过电压的计算, 得到如下主要结论:

(1) 有限电导率介质对雷电电磁场传播存在衰减作用, 随着测量点从传输线中点向端点移动, 感应过电压的幅值减小, 且电压波形的双极性特征越来越明显。

(2) 随着传输线高度的增加, 线路中点电压峰值增加, 波头上升沿时间变短, 端点电压双极性波形特征减弱, 正向电压峰值增大。因此, 在架空传输线设计时, 可以采取降低高度的方法减少线路雷电干扰。

(3) 土壤电导率对感应电压入射分量影响非常微弱, 而对散射电压分量影响较明显。随着电导率减小, 线路中点感应电压增大, 当土壤电导率大于0.1 S·m^-1时, 端点电压不再具有双极性特征。

对均匀土壤电导率情况下雷电感应电压进行研究分析, 未将电导率分层及地表地形起伏进行考虑, 这部分内容有待学者进一步研究探讨。