2. 南京信息工程大学气象灾害教育部重点实验室/气候与环境变化国际合作联合实验室/气象灾害预报预警与评估协同创新中心/中国气象局气溶胶与云降水重点开放实验室, 江苏 南京 210044;
3. 南京信息工程大学滨江学院, 江苏 南京 210044;
4. 云南电力试验研究院(集团)有限公司, 云南 昆明 650217;
5. 云南电网有限责任公司昆明供电局, 云南 昆明 650011
闪电回击的低频(Extremely Low Frequency, ELF)(30~300 kHz)和甚低频(Very Low Frequency, VLF)(3~30 kHz)信号在100~2 000 km的中距离范围内沿着有限电导率的地球表面传播(Cummer, 1997, 1998; Hu et al, 2006;刘妍秀等, 2016;张新科等, 2017;许霖等, 2017), 受到传播过程的影响, 观测到的信号明显受到衰减和变形在1 500 km以内的中距离范围内, 把地球球面假设为二维平坦面会带来明显的误差, 应该考虑到地球表面的曲面影响(Wait, 1953, 1956, 1960, 1974; Shao et al, 2009; Zhang et al, 2012a, 2012b, 2014, 2015)。从1910年起有团队开始研究天线辐射电磁场沿地表传播的基本问题, 得出了较为详细的结果, Wait(1960, 1974)给出了考虑到地球曲面变化的电磁波沿不同性质复杂地表传播的衰减函数, 但是这个衰减函数公式包含了高度震荡的艾里函数, 是一个极其复杂的微分方程, 衰减函数的求解计算非常繁琐复杂。1980年, Hill et al(1980)提出了早期计算方法来近似求解二维平坦表面上, 电磁场沿中距离传播的衰减系数, 根据不同的表面阻抗提供了不同的近似方程, 并且在求解微分方程的时候用到了四阶法Runge-Kutta方程。1993年, Maclean et al(1993)用泰勒级数法求解了衰减函数, 用泰勒展开去近似逼近真实结果。
为了计算闪电回击电磁场沿地球曲面的有限电导率地表传播的情况, 2009年Shao et al (2009)在Wait(1960, 1974)提出的计算公式的基础上做了修正, 他们用牛顿迭代法求解高度震荡的艾里函数得到了较高精确度的解, 只是迭代过程非常复杂耗时。
地闪VLF电磁脉冲沿地球表面传播是非常重要的科学问题, 这涉及到远距离雷电定位和雷电放电参量反演。本文提出了计算1 500 km以内的中距离闪电回击ELF/VLF辐射场的改进版的简易近似算法。将Wait(1960, 1974)提出的衰减函数分化为电导率衰减和地区曲率衰减两个函数, 这两个函数在频域上具有更加清晰简单的表达公式, 可以通过简单的运算计算, 免去了求解复杂的包含高震荡艾里函数的微分方程的过程。简化后使得计算效率大大提高, 同时通过精度对比, 发现提出的近似算法精度是比较理想的。因此, 该研究结果更加方便有效地解决了远距离雷电电磁波传播和放电参量的反演。
2 算法介绍 2.1 传统算法位于地球球形曲面光滑地表上的垂直电偶极子源, 在周围半径d距离处的垂直电场强度E(单位: V·m-1)为(Wait, 1960, 1974):
| $ E = {E_0}W, $ | (1) |
式中: E0为地球曲率半径无穷大电导率无穷大的理想条件下的垂直电场(单位: V·m-1); W是衰减系数。
对于电流矩为Im的电偶极子沿光滑地表产生的垂直电场E0可以用下式(Uman, 1987)近似计算:
| $ {E_0} = - \frac{1}{{2\pi {\varepsilon _0}{c^2}d}}\frac{{\partial {I_{\rm{m}}}}}{{\partial t}}, $ | (2) |
式中: Im是电流矩(单位: kA·km); d是电场源和观测点间的曲面距离(单位: m); c是光速(单位: m·s-1); ε0是介电常数; t为时间(单位: s)。
当考虑地球曲率半径与地面电导率, 闪电源与接收端均在地球表面时, 云地闪回击电磁场的计算中假设源和观测点都在地球表面, 则衰减系数W为:
| $ W = {e^{ - j{\rm{ \mathsf{ π} }}/4}}\sqrt {{\rm{ \mathsf{ π} }}x} \sum\limits_{s = 1}^\infty {\frac{{{e^{ - jx{t_s}}}}}{{{t_s} - {q^2}}}} , $ | (3) |
式中:
在计算云内放电产生的双极性窄脉冲时, 源高于地球表面之上而观测点在地球表面, Wait(1960, 1974)提出的衰减系数W为:
| $ W = 2{e^{ - j{\rm{ \mathsf{ π} }}/4}}\sqrt {{\rm{ \mathsf{ π} }}x} \sum\limits_{s = 1}^\infty {\frac{{{e^{ - jx{t_s}}}}}{{{t_s} - {q^2}}}} \frac{{{w_1}\left( {{t_s} - {y_1}} \right)}}{{{w_1}\left( {{t_s}} \right)}}\frac{{{w_1}\left( {{t_s} - {y_2}} \right)}}{{{w_1}\left( {{t_s}} \right)}}, $ | (4) |
式中:
| $ {{w'}_1}\left( t \right) - q{w_1}\left( t \right) = 0, $ | (5) |
w1(t)可以用艾里方程(Miller el at, 1946)形式表示:
| $ {w_1}\left( t \right) = \sqrt {\rm{ \mathsf{ π} }} \left[ {Bi\left( t \right) - jAi\left( t \right)} \right], $ | (6) |
为了求解ts, Shao et al(2009)使用牛顿迭代法求解高度震荡的艾里函数得到了较高的精确度, 式(5)的初解取w1(t)=0与w'(t)=0的平均值。w1(t)=0和w'(t)=0分别对应|q|=∞与|q|=0。只是迭代过程非常复杂耗时, 因为艾里函数在整个复平面上高度震荡, 必须在不同的角频率不同的电导率重复迭代很多次。但是这种计算方法精度很高, 因此我们将其结果作为“真值”, 对本文的简易近似算法做对比。
2.2 改进算法本文将传统算法的衰减因子划分为曲率衰减因子和电导率衰减因子。理想场对两衰减因子均进行卷积后, 既考虑到地球曲率的影响, 又考虑到地面电导率带来的影响。同时由于两衰减因子是相互独立的, 对两因子进行卷积之后不会影响计算结果, 且两因子表达简洁, 计算方便。
| $ W = {W_\sigma }{W_\rho }, $ | (7) |
式中: σ代表地表电导率(单位: S·m-1); ρ代表地球表面曲率; Wσ仅带表电导率衰减因子, 不考虑地球表面曲面的影响, 可表示为:
| $ {W_\sigma } = 1 - j\sqrt {{\rm{ \mathsf{ π} }}p} \exp \left( { - p} \right){\rm{erfc}}\left( {j\sqrt p } \right), $ | (8) |
| $ p = - j\omega d{\Delta ^2}/\left( {2c} \right), $ | (9) |
式中: erfc表示误差方程; d是闪电通道与观测点之间距离(单位: km); ω表示角频率(单位: rad·s-1); c表示光速(单位: m·s-1); 其他符号与式(4)一致。
衰减函数Wρ仅代表地球表面曲面衰减因子, 不考虑有限电导率的影响。当地面电导率无穷大时, 由q=-j(k0Re/2)1/3Δ可以推出q=0, 式(3)可以简化为:
| $ {W_1} = {e^{ - j{\rm{ \mathsf{ π} }}/4}}\sqrt {\pi x} \sum\limits_{s = 1}^\infty {\frac{{{e^{ - jx{t_s}}}}}{{{t_s}}}} , $ | (10) |
Sollfrey(1968)指出, ts可表示为:
| $ {t_s} = {e^{ - j{\rm{ \mathsf{ π} }}/3}}{\left( {3{\rm{ \mathsf{ π} }}{v_s}/2} \right)^{2/3}}, $ | (11) |
| $ {v_s} = s - 3/4 - 0.00795/\left( {s - 3/4} \right),\;\;\;\;\;s = 1.2, \cdots $ | (12) |
式中: s的取值为0, 1, 2, 3, …。其中s=0时误差为0, s=1时误差为0.002 4, s=2时误差小于0.001 2, s取值越大, 误差越小, 在大于2时误差均小于0.000 5。把式(11)中求出的ts代入式(10), 即可求出地球曲率衰减因子W1。
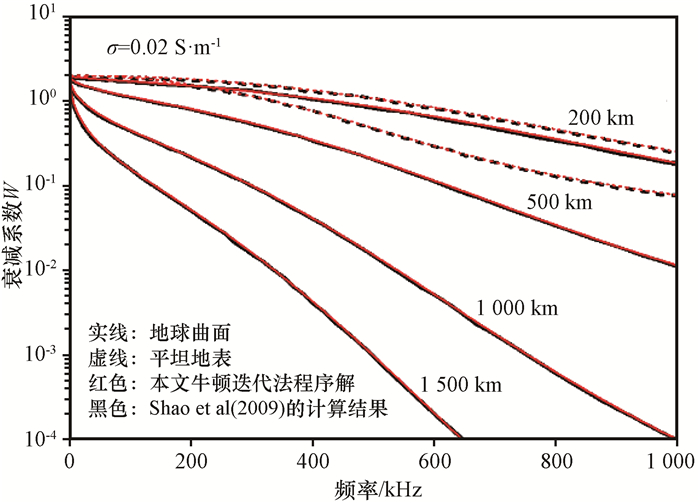
3 结果分析 3.1 结果验证首先编写了利用牛顿迭代法求解衰减系数W的程序, 为了验证本程序的正确性, 将计算结果与Shao et al(2009)的结果进行对比[图 1, 红色实线是电导率为0.02 S·m-1考虑地球曲面时本文牛顿迭代法对于衰减系数W求解结果, 黑色实线是电导率为0.02 S·m-1考虑地球曲面时Shao et al(2009)对于衰减系数W求解结果, 红色虚线是电导率为0.02 S·m-1平坦地面时本文牛顿迭代法对于衰减系数W求解结果, 黑色虚线是电导率为0.02 S·m-1平坦地面时Shao et al(2009)对于衰减系数W求解结果], 衰减系数W在频域范围从0~1 000 kHz, 地面电导率设为0.02 S·m-1, 闪电回击电场源和观测点都在地表。结果发现本牛顿迭代法程序求得的根与Shao et al(2009)的结果一致, 证明了本程序是正确的。
|
图 1 牛顿迭代法求解程序和Shao et al(2009)对于衰减系数W求解结果对比 Figure 1 Comparison of the simulated amplitude of attenuation functions W in the frequency domain by our Newton-Raphson root-finding codes and that presented by Shao et al (2009) |
为了验证中距离闪电回击辐射场的改进版近似算法的正确性, 文章使用的电流源是由(Jones, 1970)提出的电流矩模型, 表达式为:
| $ {I_{\rm{m}}}\left( t \right) = {I_0}\frac{{{v_0}}}{\gamma }\left[ {{e^{ - at}} - {e^{ - bt}}} \right]\left[ {1 - {e^{ - \gamma t}}} \right], $ | (13) |
式中:
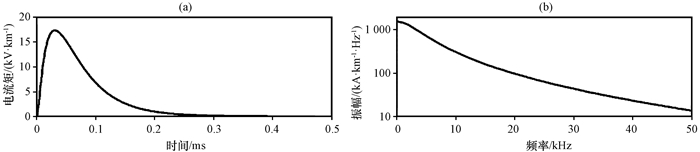
图 2别给出了这一电流矩的波形与频谱图, 相较于8/20波形与10/350波形, 这种电流矩波形时间更长, 包含更多低频成分, 更适用于研究长距离电磁场的传播。
|
图 2 电流矩时域波形(a)与频谱(b)分布 Figure 2 The current moment waveshape in time domain (a) and in frequency domain (b) used for computing the lightning VLF radiation at an intermediate distance |
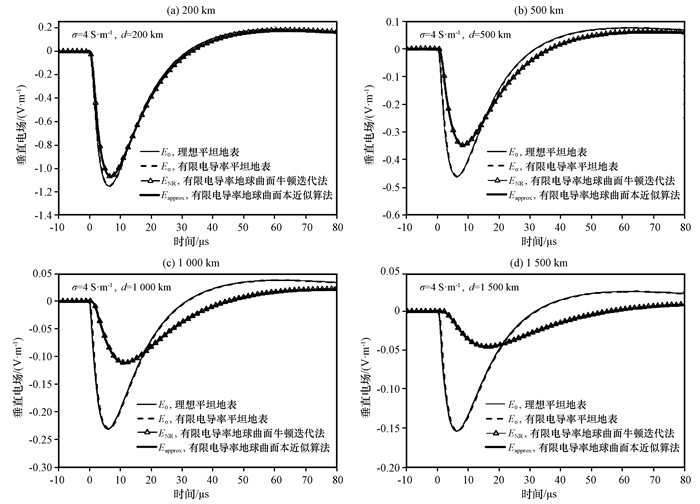
在考虑到地球表面曲面和海洋传播距离的情况下, 采用本文近似算法Eapprox和Shao et al (2009)提出的牛顿迭代法ENR结果对比(图 3)可以看到两者具有相同的结果。对于电导率为4 S·m-1的光滑海洋路径, 在几千到几百千米的范围内有限电导率对于甚低频闪电回击电磁场并没有影响。但是在雷暴天气, 大风会将海面吹起波浪变得粗糙, 根据Zhang et al (2012b)的研究结果, 粗糙海洋表面对10 MHz以上的分量影响明显。
|
图 3 考虑到地球表面曲面和海洋传播距离的情况下, 采用本文近似算法Eapprox和Shao et al(2009)提出的牛顿迭代法ENR结果对比 Figure 3 Comparison of the vertical electric field calculated by our approximated method and the Newton-Raphson root-finding method presented by Shao et al (2009) for the ocean propagation path considering the earth curvature at different distances |
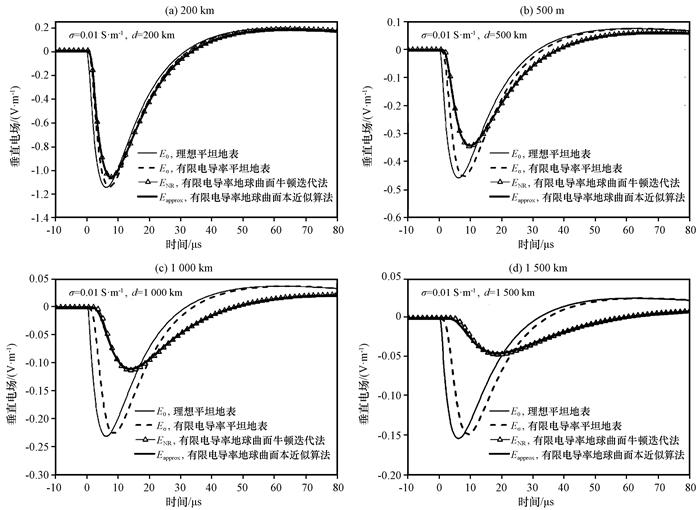
相对于海洋电导率, 地球表面的曲面对于闪电回击电磁场的传播具有较大的影响, 随着距离的变大, 影响越来越明显。200 km以内地球表明曲面可以近似忽略, 但当观测距离超过500 km时地球曲面造成的衰减大约为22%, 当观测距离超过1 000 km时地球曲面造成的衰减大约为52%。在考虑到地球曲面影响的情况下, 图 4和图 5分别在电导率为0.01 S·m-1和0.001 S·m-1时, 进一步对比了本研究中近似算法和牛顿迭代算法的结果。通过表 1和表 2列出的近似算法幅值和波头时间参量误差情况可以看到, 近似算法也可以得到较为准确的幅值、波头时间等参量, 证明本近似算法非常可靠, 可以在中距离模拟闪电辐射场的波形。本文近似算法在计算中距离闪电辐射场幅值时对于地面电导率为4, 0.01和0.001 S·m-1的情况计算误差分别为0.2%, 3.3%和8.7%。
|
图 4 电导率为0.01 S·m-1时采用近似算法Eapprox和Shao et al (2009)提出的牛顿迭代法ENR结果对比 Figure 4 Comparison of the vertical electric field calculated by our approximated method and the Newton-Raphson root-finding method presented by Shao et al (2009) for the ocean propagation path considering the earth curvature at different distances, but for finite conductivity of 0.01 S·m-1 |
|
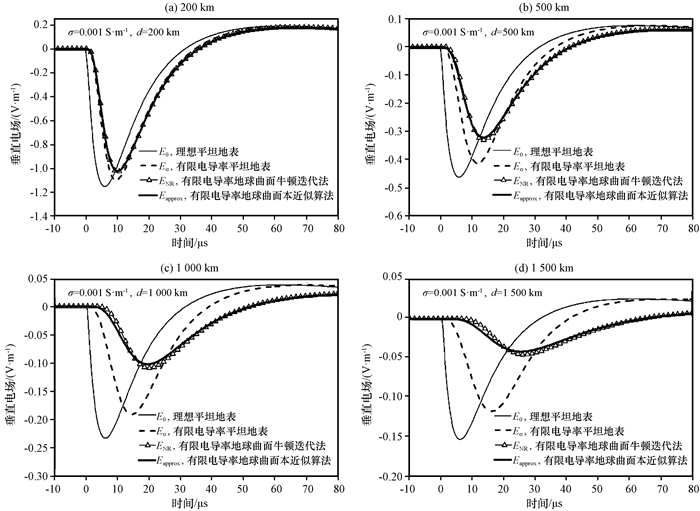
图 5 电导率为0.001 S·m-1时采用近似算法Eapprox和Shao et al (2009)提出的牛顿迭代法ENR结果对比 Figure 5 Comparison of the vertical electric field calculated by our approximated method and the Newton-Raphson root-finding method presented by Shao et al (2009) for the ocean propagation path considering the earth curvature at different distances, but for finite conductivity of 0.001 S·m-1 |
| 表 1 本文近似算法幅值误差情况统计 Table 1 Statistic errors analysis of peak values |
| 表 2 本文近似算法波头时间误差情况统计 Table 2 Statistic errors analysis of rise time port |
作为对照, 本文也计算了平滑传播路径, 如图 4、图 5的E0, 说明随着电导率的减小, 辐射场的传播效率加强。高频分量被选择性的衰减掉, 衰减会造成电磁场幅值的减小和波头时间的增加(Cooray et al, 2000, 2008, 2009, 2014; Delfino et al, 2008a, 2008b)。因此中距离范围内, 在电导率小于0.01 S·m-1时有限电导率地表应该考虑其衰减作用。
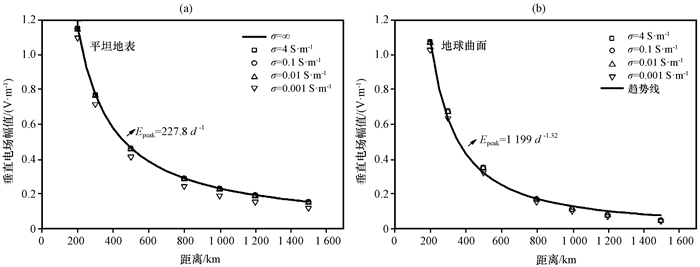
3.2 闪电回击ELF/VLF辐射电场值和水平传播距离的关系从不同电导率时采用近似算法Eapprox和Shao et al (2009)提出的牛顿迭代法ENR结果对比(图 4, 图 5)可见, 闪电回击ELF/VLF电场幅值Epeak(单位: V·m-1)沿地球曲面有限电导率传播时有很大衰减, 在中距离地球曲面衰减影响比有限电导率的衰减影响更为明显。在图 6进一步对比平坦地面和地球曲面的衰减情况, 对于地球曲面, 电场幅值在水平距离d(单位: km)范围处的增益为d-1.32。因此, 在几百到几千公里的中距离闪电回击低频辐射场的传输中, 衰减更多的是受地球曲面影响形成。
|
图 6 电场幅值绝对值与距离的关系 Figure 6 The absolute value of field peak as a function of propagation distance |
本文提出了一种新的近似方法来计算1 500 km以内的中距离闪电回击ELF/VLF电磁波传播情况, 得出以下结论:
(1) 通过用传统牛顿迭代法在不同的地表电导率下验证了文本近似算法的正确性, 验证结果证明本文近似算法计算的电场幅值和波头时间都非常准确。将电磁波沿不同性质复杂地表传播的衰减函数在频域上分化为电导率衰减和地表曲率衰减两个函数的卷积, 这样衰减函数的物理意义更为明确, 计算过程大幅简化。
(2) 当地表电导率大于0.01 S·m-1时, 电导率因子对中距离闪电回击ELF/VLF辐射场幅值几乎没有影响。
(3) 地球曲面对中距离电磁场的传播具有明显的影响。比如, 在地球曲面的影响下1 500 km处闪电回击ELF/VLF辐射电磁场的幅值仅仅为平坦地表情况的30%~40%, 500 km处闪电回击ELF/VLF辐射电磁场的幅值仅仅为平坦地表情况的75%~80%。
(4) 对于平坦地面, 电场幅值Epeak在水平距离d范围处的增益为d-1.32。因此在几百到几千公里的中距离闪电回击低频辐射场的传输中, 衰减更多的是受地球曲面影响形成。如果没有考虑地球曲面衰减的影响会错误的计算到比真实值小的电场幅值。
Cooray V, Fernando M, Sorensen T. 2000. Propagation of lightning generated transient electromagnetic fields over finitely conducting ground[J]. Atmos Terr Phys, 62: 583–600.
DOI:10.1016/S1364-6826(00)00008-0 |
|
Cooray V, 2014. The lightning flash[M]. Stevenage: The Institution of Engineering and Technology.
|
|
Cooray V. 2008. On the accuracy of several approximate theories used in quantifying the propagation effects on lightning generated electromagnetic fields[J]. IEEE Trans Antennas Propag, 56(7): 1960–1967.
DOI:10.1109/TAP.2008.924680 |
|
Cooray V. 2009. Propagation on effects due to finitely conducting ground on lightning-generated magnetic fields evaluated using Sommerfeld's integrals[J]. IEEE Trans Electromagn Compat, 51(3): 526–531.
DOI:10.1109/TEMC.2009.2019759 |
|
Cummer S A, 1997. Lightning and ionospheric remote sensing using VLF/ELF radio atmospherics[D]. Palo Alto: Stanford University.
|
|
Cummer S A, Inan U S, Bell T F. 1998. Ionospheric D region remote sensing using VLF radio atmospherics[J]. Radio Sci, 33(6): 1781–1792.
DOI:10.1029/98RS02381 |
|
Delfino F, Procopio R, Rossi M. 2008a. Lightning return stroke current radiation in presence of a conducting ground:1.Theory and numerical evaluation of the electromagnetic fields[J]. Geophys Res, 113: D05110.
|
|
Delfino F, Procopio R, Rossi M. 2008b. Lightning return stroke current radiation in presence of a conducting ground:2.Validity assessment of simplified approaches[J]. Geophys Res, 113: D05111.
|
|
Hill D A, Wait J R. 1980. Ground wave attenuation function for a spherical earth with arbitrary surface impedance[J]. Radio Sci, 15(3): 637–643.
DOI:10.1029/RS015i003p00637 |
|
Hu W, Cummer S A. 2006. An FDTD model for low and high altitude lightning-generated EM fields[J]. IEEE Trans Antennas Propag, 54(5): 1513–1522.
DOI:10.1109/TAP.2006.874336 |
|
Jones D L. 1970. Electromagnetic radiation from multiple return strokes of lightning[J]. Journal of Atmospheric and Solar-Terrestrial Physics, 32(6): 1077–1093.
DOI:10.1016/0021-9169(70)90119-4 |
|
Maclean T S M, Wu Z, 1993. Radiowave propagation over ground[M]. London: Chapman & Hall.
|
|
Miller J C P, 1946. The airy integral[D]. New York: Cambridge University.
|
|
Shao X M, Jacobson A R. 2009. Model simulation of very low-frequency and low-frequency lightning signal propagation over intermediateranges[J]. IEEE Transactions on Electromagnetic Compatibility, 51(3): 519–525.
DOI:10.1109/TEMC.2009.2022171 |
|
Uman M A, 1987. The lightning discharge[M]. San Diego: Courier Corporation.
|
|
Wait J R. 1953. Radiation from a vertical electric dipole over a stratifiedground[J]. Transactions of the IRE Professional Group on Antennas and Propagation, 1(1): 9–11.
DOI:10.1109/T-AP.1953.27320 |
|
Wait J R. 1956. Radiation from a vertical antenna over a curved stratified ground[J]. Journal of Research of the National Bureau of Standards, 56(4): 237–244.
DOI:10.6028/jres.056.031 |
|
Wait J R. 1960. On the excitation of electromagnetic surface waves on a curvedsurface[J]. IRE Transactions on Antennas and Propagation, 8(4): 445–448.
DOI:10.1109/TAP.1960.1144862 |
|
Wait J R. 1974. Recent analytical investigations of electromagnetic ground wave propagation over inhomogeneous earthmodels[J]. Proceedings of the IEEE, 62(8): 1061–1072.
DOI:10.1109/PROC.1974.9570 |
|
Zhang Q L, Jing X Q, Yang J, et al. 2012a. Numerical simulation of the lightning electromagnetic fields along a rough and ocean-land mixed propagation path[J]. Geophys Res, 117: D20304.
|
|
Zhang Q L, Yang J, Li D S, et al. 2012b. Propagation effects of a fractal rough ocean surface on the vertical electric field generated by lightning return strokes[J]. J Electrostatics, 70(1): 54–59.
DOI:10.1016/j.elstat.2011.10.003 |
|
Zhang Q, Hou W, Ji T, et al. 2014. Validation and revision of far-field-current relationship for the lightning strike to electrically short objects[J]. Journal of Atmospheric and Solar-Terrestrial Physics, 120: 41–50.
DOI:10.1016/j.jastp.2014.08.015 |
|
Zhang Q L, Ji T T, Hou W H. 2015. Effect of frequency-dependent soil on the propagation of electromagnetic fields radiated by subsequent lightning strike to tall objects[J]. IEEE Transactions on Electromagnetic Compatibility, 57(1): 112–120.
DOI:10.1109/TEMC.2014.2361926 |
|
刘妍秀, 张广庶, 王彦辉, 等. 2016. 闪电VHF辐射源功率观测及雷暴电荷结构的初步分析[J]. 高原气象, 35(6): 1662–1670.
Liu Y X, Zhang G S, Wang Y H, et al. 2016. Preliminary analysisof the VHF lightning radiation pulse power and charge structure in a thunderstorm[J]. Plateau Meteor, 35(6): 1662–1670.
DOI:10.7522/j.issn.1000-0534.2016.00051 |
|
张新科, 陈晋北, 余晔, 等. 2017. 雷暴系统影响下的黄土高原塬区微气象特征研究[J]. 高原气象, 36(2): 384–394.
Zhang X K, Chen Jinbei, Yu Ye, et al. 2017. Study on the micrometeorological characteristics over the Loess Plateau under the influence of thunderstorm[J]. Plateau Meteor, 36(2): 384–394.
DOI:10.7522/j.issn.1000-0534.2017.00002 |
|
许霖, 姚蓉, 王晓雷, 等. 2017. 湖南省雷暴大风的时空分布和变化特征[J]. 高原气象, 36(4): 993–1000.
Xu L, Yao R, Wang X L, et al. 2017. Study of temporal-spatial distribution and variation characteristics of thunderstorm gales in Hunan[J]. Plateau Meteor, 36(4): 993–1000.
DOI:10.7522/j.issn.1000-0534.2016.00088 |
2. Key Laboratory of Meteorological Disaster, Ministry of Education(KLME)/Joint International Research Laboratory of Climate and Environment Change(ILCEC)/Collaborative Innovation center on Forecast and Evaluation of Meteorological Disaster(CIC-FEMD)/Key Laboratory for Aerosol-Cloud-Precipitation of China Meteorological Administration, Nanjing University of Information Science and Technology, Nanjing 210044, Jiangsu, China;
3. Binjiang College of NanjingUniversity of Information Science and Technolog, Nanjing 210044, Jiangsu, China;
4. Yunnan Electric Power Test & Research Institute(Group) Co., Ltd, Kunming 650217, Yunnan, China;
5. Kunming Power Supply Bureau, Kunming 650011, Yunnan, China
 2018, Vol. 37
2018, Vol. 37