2. 中国科学院大气物理研究所大气科学和地球流体力学数值模拟国家重点实验室, 北京 100029;
3. 中国科学院大学, 北京 100049
青藏高原(下称高原)位于副热带欧亚大陆的中东部, 是世界上海拔最高, 地形最复杂的高原。高原作为一个巨大的抬升热源(Flohn, 1957;叶笃正等, 1979), 可以直接加热对流层中部大气, 加强亚洲季风环流, 且能够显著的影响中国地区的降水(He et al, 1987; Yanai et al, 1992; Ye et al, 1998; Wu et al, 1998; Qian et al, 2004; Liu et al, 2007;周俊前等, 2016;张长灿等, 2017;庞轶舒等, 2017;王顺久, 2017;卓嘎等, 2017)。高原感热是热源的一个主要分量, 在过去几十年中被学者们大量的研究。高原感热加热通过“青藏高原感热气泵(TP-SHAP)”理论在春夏季高原近地层产生正涡度和辐合, 造成水汽从热带海洋向亚洲陆地输送, 同时在对流层上层产生负涡度, 形成高空的辐散运动, 影响和调节高原及其周边地区的大气环流和亚洲季风过程(吴国雄等, 1997, 2016; Wu et al, 2007, 2012;刘屹岷等, 2017)。Duan et al(2013)研究认为高原春季感热对东亚夏季风的爆发时间有很强的调制作用。
诸多学者利用中国气象局提供的站点数据计算高原地区的地表感热通量(叶笃正等, 1979;陈万隆等, 1984; Chen et al, 1985; Li et al, 1996;李国平等, 2000; Duan et al, 2008; Yang et al, 2011;王美蓉等, 2012)。这些研究是利用总体动力学公式:
| $ SH = \rho {C_p}{C_H}V({T_g} - {T_a}){\rm{ }}, $ | (1) |
式中: ρ为空气密度(单位: kg·m-3); Cp= 1 005 J·kg-1·K-1, 为干空气定压比热; CH为热量拖曳系数, 无量纲量; V为10 m风速(单位: m·s-1); Tg为0 cm地表温度(单位: ℃); Ta为2 m空气温度(单位: ℃)。高原上CH的参数化方案有很多种, 主要归纳为两类:一类为常值类, 对某些特殊地区CH曾取值为0.008(叶笃正等, 1979), 但诸多研究表明高原CH取常数0.004(CHC)更为合理(Chen et al, 1985;陈隆勋等, 1991; Li et al, 1996; Duan et al, 2008)。另一类是风速函数类, 陈万隆等(1984)给出此类CH(CHV)的表达式为:
| $ {C_{HV}} = \left\{ \begin{array}{l} 0.{\rm{ }}001{\rm{ }}12 + 0.{\rm{ }}01/V{\rm{ }}, \;\;\;Z > 2{\rm{ }}800{\rm{m}}\\ 0.{\rm{ }}001{\rm{ }}12 + 0.{\rm{ }}01/V - 0.{\rm{ }}003{\rm{ }}62({P_s} - 720)/280{\rm{ }}, \;\;\;Z \le 2{\rm{ }}800{\rm{m}} \end{array} \right. $ | (2) |
式中: Ps为本站气压(单位: hPa); Z为站点海拔(单位: m)。
Yang et al(2011)比较了基于CHC和CHV计算的地表感热, 发现它们的变化趋势相反。在计算地表感热时, 密度ρ的取值也存在差异。有的取为常值0.8 kg·m-3(ρC)(叶笃正等, 1979; Duan et al, 2008;王美蓉等, 2012);有的则由干空气状态方程ρRT=Ps/(RTa)确定(王慧等, 2010), 其中R=287.04 J·K-1·kg-1, 为干空气比气体常数。但很少有研究分析这两种密度取值对地表感热计算的不同影响。已有诸多研究认为, 从20世纪80年代到21世纪00年代初, 春夏季高原地表感热和表面风速均经历了一个显著的年代际减弱, 而地温、气温和地气温差均是增加的。而且在年代际时间尺度上, 由于CH取常值, 密度相对变化很小, 而表面风速的相对变化比地气温差的相对变化约大一个量级, 所以他们定性的指出表面风速是地表感热年代际减弱的一个主要原因(Duan et al, 2008; Liu et al, 2012;王美蓉等, 2012; Yang et al, 2014)。
以上研究均是针对某个海拔以上的地表感热进行分析, 而很少有工作分析不同海拔上的地表感热特征, 尤其是对“青藏高原感热气泵(TP-SHAP)”理论形成起着重要作用的高原侧边界地表感热的特征(Wu et al, 2007)。那么, 在不同季节和不同海拔上, 地表感热的气候态及其变化特征是怎样的?CH和ρ对地表感热计算有何影响?如何定量分析表面风速与地气温差对地表感热变化的相对贡献?这将是本文关注的主要问题。
利用1961-2014年中国气象观测站逐日常规资料, 分析在不同季节和不同海拔上高原地表感热的气候态特征以及CH和ρ对其计算的影响, 并研究高原地表感热的年际、年代际以及趋势变化的时空分布特征, 最后结合偏相关和多元线性回归方法, 定量的分析表面风速与地气温差在年际和年代际时间尺度上对地表感热变化的相对贡献。
2 资料选取和方法介绍 2.1 资料选取使用的资料是由中国国家气象信息中心《中国国家级地面气象站基本气象要素定时值数据集(V3.0)》(任芝花等, 2012)提供的全中国2 474个站一日4次[02:00(北京时, 下同), 08:00, 14:00和20:00]常规气象观测资料。物理量包括Ps、Ta、Tg和V。因为20世纪60年代之前高原站点少, 气象观测资料质量差, 故本文分析的时段为1961-2014年。研究中, 春季定义为3-5月平均、夏季为6-8月平均、秋季为9-11月平均、冬季为当年12月至次年2月平均。
Duan et al(2008)指出, Tg在1961-2003年的缺测率接近8%, 主要发生在20世纪80年代之前, 而Ta等观测资料在该段时间内的缺测率则小于0.5%。为了得到比较合理的站点数据, 站点处理方式为选取Tg 4个时次(02:00, 08:00, 14:00和20:00)均满足每年非缺测值大于等于300个的有效站点, 得到1961-2014年海拔位于H1500-2000(1 500~2 000 m)、H2000-3000(2 000~3 000 m)和H3000(高于3 000 m)的站点数分别为57, 22和20个站(统称为61_站点); 1979-2014年海拔位于H1500-2000、H2000-3000和H3000的站点数分别为84、43和31个站(统称为79_站点)。测站主要分布在西藏、青海、甘肃、四川、云南等省(图 1), 为了方便, 本文把测站分布位置统称为高原。
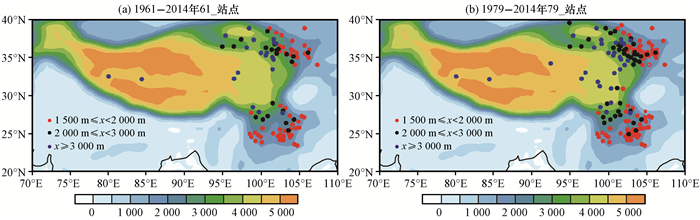
|
图 1 青藏高原1961-2014年61_站点(a)和1979-2014年79_站点(b)的空间分布 彩色区表示海拔(单位: m) Figure 1 The spatial distribution of 61_ stations during 1961-2014 (a) and 79_ stations during 1979-2014 (b) over the Qinghai-Tibetan Plateau. Color area denotes altitude (unit: m) |
利用公式(1)来计算地表感热, 如无特别说明, 热量拖曳系数CHC=0.004, 密度取为ρRT。
2.2.2 统计方法由于表面风速与地温、气温可能存在相互作用(Liu et al, 2012), 为了更准确的区分表面风速与地气温差对地表感热的相对贡献, 采用偏相关(Zar, 1999)和多元线性回归方法, 来比较两者与地表感热变化的密切程度。偏相关关系可由以下公式进行计算:
| $ {r_{12, {\rm{ }}3}} = \frac{{{r_{12}} - {r_{13}}{r_{23}}}}{{\sqrt {(1 - r_{13}^2)(1 - r_{23}^2)} }}{\rm{ }}, $ | (3) |
式中:下标1代表地表感热; 下标2代表表面风速; 下标3代表地气温差; r皆为普通的相关系数, 例如r12表示地表感热与表面风速的相关系数, r12, 3则表示去除地气温差影响的地表感热与表面风速的相关系数。t检验用于判断偏相关系数置信度水平。
由最小二乘法得到的多元线性回归方程可依如下公式进行计算:
| $ y = {\beta _0} + {\beta _1}{x_1} + {\beta _2}{x_2}, $ | (4) |
式中: x1为标准化的表面风速; x2为标准化的地气温差; y为标准化的地表感热; β0为方程回归系数; β1为表面风速的回归系数; β2为地气温差的回归系数。F检验用于判断回归方程置信度水平, t检验用于判断各个回归系数的置信度水平。
本文在分析年际变化时用到的年际增量定义为当年的值减去前一年的值, 它表征了年与年之间的差异(Fan et al, 2008)。用年际增量序列求相关比用原始序列求相关能更好的反映出两个序列在年际变化上的相关程度。文中的线性变化趋势由最小二乘法计算, t检验用于判断其置信度水平。
本文用到的其他统计方法有滑动平均、相关分析、经验正交函数EOF分解、Lanczos滤波。
3 高原地表感热特征 3.1 气候态特征在讨论高原地表感热变化特征之前, 先分析其气候平均的空间分布和季节演变特征。
图 2为1979-2014年高原79_站点平均的地表感热SH、表面风速V和地气温差Tg-Ta在不同季节下和不同海拔上的分布。如图 2所示, 春季, SH、V和Tg-Ta均随高度上升而增加, 最大值分布于H3000, 分别为64.21 W·m-2、2.73 m·s-1和4.39 ℃, 最小值位于H1500-2000, 分别为58.05 W·m-2、2.41 m·s-1和3.76 ℃。Duan et al(2014)和Wu et al(2017)指出气候态下高原春季V随高度上升而增加, Tg和Ta均随高度上升而减少, 但Tg比Ta减少的慢, 所以Tg-Ta也随高度上升而增加。因为SH取决于V和Tg-Ta, 故SH也随高度上升而增加。这是由于在对流—辐射—平衡(CRE)约束下(Molnar et al, 1999), Tg的垂直递减率约为3 ℃·km-1, 小于标准大气垂直递减率6 ℃·km-1。夏秋两季的SH、V和Tg-Ta也均随高度上升而增加。冬季, SH和Tg-Ta最大值均出现在H1500-2000, 分别为29.18 W·m-2和1.62 ℃, 最小值均位于H2000-3000, 分别为24.98 W·m-2和1.16 ℃; V随高度上升而增加, 最大和最小值分别为2.19 m·s-1和1.91 m·s-1。
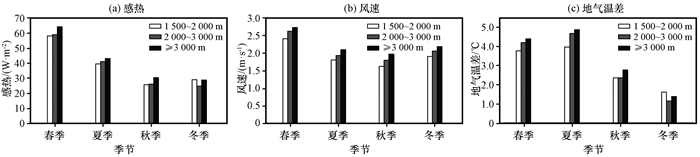
|
图 2 1979-2014年青藏高原79_站点平均感热、风速和地气温差在春季、夏季、秋季和冬季的海拔分布 Figure 2 The distribution of 79_ stations average sensible heating, wind speed and ground-air temperature difference over the Qinghai-Tibetan Plateau in different seasons and at different elevations during 1979-2014 |
就高原整体而言, SH和V均在春季最大, 分别为60.42 W·m-2和2.59 m·s-1, 在秋季最小, 分别为27.49 W·m-2和1.80 m·s-1, 其中SH冬季的值与秋季相当; Tg-Ta的季节变化与张文纲等(2006)结果一致, 最大和最小值分布于夏季和冬季, 分别为4.50 ℃和1.39 ℃。这是因为夏季湍流交换最强, 冬季湍流交换最弱的缘故(杨智等, 2010)。年平均状况而言, 本文高原79_站点区域平均的SH为39.22 W·m-2, 约为叶笃正等(1979)所给值的一半, 比Yang et al(2011)的结果小15 W·m-2左右, 但与Duan et al(2008)和王美蓉等(2012)等得到的40 W·m-2基本相同, 这主要与计算方案和CH的选取有关。
以上分析表明, 1979-2014年高原地表感热、表面风速以及地气温差随着高度上升而增加。春季, 地表感热从H1500-2000的58.05 W·m-2增加到H3000的64.21 W·m-2。季节变化规律表现为地表感热和表面风速均在春季最大秋季最小, 地表感热在冬季的值与秋季相当, 地气温差最大和最小值则分布于夏季和冬季。
高原地形复杂, 天气气候具有明显的局地特征。图 3给出了1979-2014年平均的高原79_站点春夏两季SH、V和Tg-Ta的空间分布。如图 3所示, 春季95°E以西的有限几个站中有4个站地表感热较大, 达到90 W·m-2; 95°E以东SH、V和Tg-Ta均是高原东南部为大值区, 东北部为小值区。而夏季95°E以东SH、V和Tg-Ta则是南部为小值区, 北部为大值区, 夏季SH的分布与Zhu et al(2012)的结果类似。
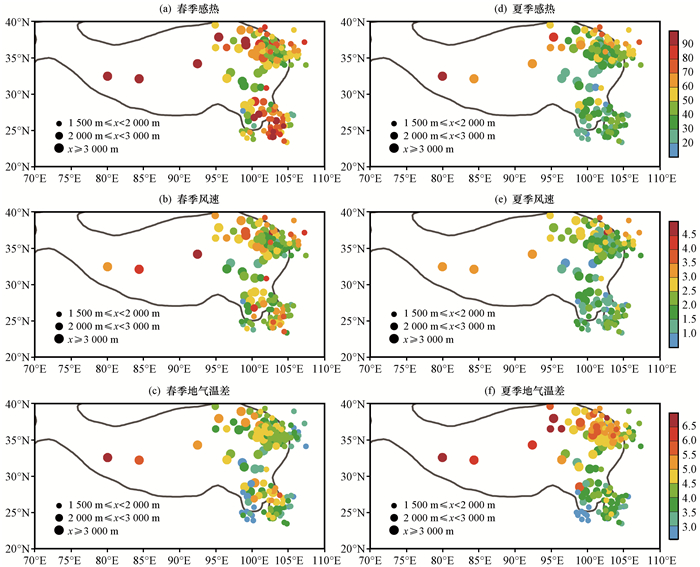
|
图 3 1979-2014年平均的青藏高原79_站点春季, 夏季感热(单位: W·m-2)、风速(单位: m·s-1)和地气温差(单位: ℃)的空间分布 灰色轮廓线是海拔为2 000 m的等值线 Figure 3 The spatial distribution of 79_ stations sensible heating (unit: W·m-2), wind speed (unit: m·s-1) and ground-air temperature difference (unit: ℃) over the Qinghai-Tibetan Plateau in spring and summer on the average of 1979-2014. Gray line indicates the elevation of 2 000 m |
由公式(1)可知, CH对地表感热计算有显著的影响。Yang et al(2011)比较CHC和CHV计算的高原平均地表感热, 结果表明在1984-2006年, 前者量值在1-12月中每月的气候态均比后者小, 相差均在10 W·m-2之内, 在年平均情况下, 前者的趋势变化率为-2.5 W·m-2·(10a)-1, 后者为0.3 W·m-2·(10a)-1, 两者趋势变化呈相反特征。
本文区分H1500-2000、H2000-3000和H3000三种海拔, 进一步分析在春夏两季不同海拔上不同CH方案对地表感热计算的影响。
SH1、SH2、SH3、PSH1和PSH2的定义见表 1, 表 2为它们在春季H3000上的相关系数, 图 4则给出了它们在高原春夏两季三种海拔上的时间序列。
| 表 1 青藏高原不同气象变量和参数的定义 Table 1 The definition of different meteorological variables and parameters over the Qinghai-Tibetan Plateau |
| 表 2 春季青藏高原(海拔高于3 000 m)不同气象变量和参数的相关系数 Table 2 The correlation coefficient between different met- eorological variables and parameters over the Qinghai- Tibetan Plateau (elevation over 3 000 m) in spring |
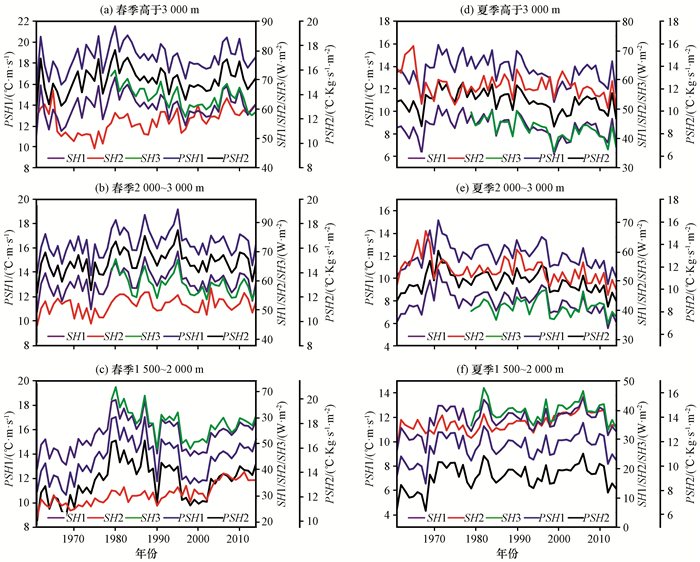
|
图 4 青藏高原1961-2014年61_站点平均的SH1、SH2、PSH1和PSH2以及1979-2014年79_站点平均的SH3在春季和夏季不同海拔上的时间序列 Figure 4 Time series of 61_ stations average SH1, SH2, PSH1 and PSH2 during 1961-2014 and 79_ stations average SH3 during 1979-2014 at different elevations over the Qinghai-Tibetan Plateau in spring and summer |
由公式(2)可知, CHV主要由表面风速所决定, 所以表面风速在不同季节和不同海拔上的分布差异会导致CHV的不同, 进而使得SH1与SH2在不同季节和不同海拔上产生显著的差异。对于较高海拔(高于2 800 m), 当CHV大于CHC, 即表面风速小于3.47 m·s-1时, SH2大于SH1。值得注意的是, 在计算CHV时, 如果位于分母的表面风速为0 m·s-1, 则设为缺测。而在计算多年平均表面风速时, 对于表面风速为0 m·s-1的值, 依然当做有效值处理, 所以图 2(b)中的平均表面风速会比计算CHV时采用的平均表面风速小。
由图 4可知, SH1和SH3在春夏两季三种海拔上, 两者不论大小、年际变化还是更长时间变化均非常接近, 而且从表 2也可以看出, SH1与SH3的相关系数高达0.89, 说明两者的线性相关非常高。上述分析表明, 61_站点资料与79_站点资料计算结果基本一致。
从图 4中可以看出, 就1961-2014年气候平均而言, 春季三种海拔上, SH1均比SH2大, 其中在H1500-2000上相差最大为22.74 W·m-2, 在H3000上相差最小为5.04 W·m-2; 夏季H2000-3000和H3000上SH2均比SH1大, 且H3000上相差最大为14.3 W·m-2。而H1500-2000上SH2与SH1基本相当。对比春夏两季, 在三种海拔上, SH1春季均比夏季大, 而SH2春季均比夏季小。平均而言, 1979-2003年, SH1在春夏两季三种海拔上呈减弱趋势, 与Duan et al(2008)、Yang et al(2011)和Liu et al(2012)的研究结果一致, 而SH2呈微弱上升趋势, 与Yang et al(2011)的研究结果一致。且由表 2可知, SH1与SH2的相关系数只有0.27, 说明它们之间的相关程度不高。总体而言, 在三种海拔上, 春季SH1大于SH2, 夏季SH1小于SH2。1979-2003年SH1为减弱趋势, 而SH2则是上升趋势。
CHC和CHV两种计算方案中, 哪一种能够更为合理地表征地表感热特征?Yang et al(2009)基于微气象学的相似理论和湍流实验观测资料, 在考虑热交换系数的日变化基础上, 发展了应用台站资料计算地表感热通量的方法(下称Yang方案), 并计算了高原地表感热通量的气候态特征以及1984-2006年的变化趋势(Yang et al, 2011)。Yang方案中, 高原地表感热通量春季平均大于夏季平均, 且在1984-2006年间为减弱趋势, 这与CHC计算的地表感热特征基本一致。由此可见使用热量拖曳系数CHC比CHV能够较为合理地表征地表感热特征。
下面进一步探究在不同季节和不同海拔上ρC和ρRT对地表感热计算的影响, 这里暂不考虑CH的作用。如图 4所示, PSH1和PSH2在春夏两季三种海拔上, 两者的年际变化和更长时间变化均十分一致, 而且从表 2也可以看出, PSH1与PSH2的相关系数高达0.99, 说明两者之间线性相关非常高。这是由于ρRT在固定高度上均约为常数的缘故。在春季H1500-2000、H2000-3000和H3000上分别约为0.97、0.91和0.82 kg·m-3。夏季在对应高度上均比春季小约0.02 kg·m-3。综上所述, 用以上两种密度计算的地表感热, 在年际变化和更长时间变化上是十分一致的, 不过在量值上有细微差别, ρC方案小于ρRT方案。而Yang方案中, 高原各个季节平均的地表感热通量均比本文所有计算方案得到的地表感热通量都大, 所以ρRT方案与Yang方案结果更为一致。因此, 下面分析地表感热的年际与年代际变化时, 均使用ρRT和常数CHC。
4 高原地表感热年际变化特征相关系数是反映两个变量之间线性相关关系密切程度的统计指标。为了进一步探究SH1、SH2、SH3、PSH1、PSH2之间的年际变化相关程度, 本文对春季H3000上的这五个变量计算其年际增量, 得到对应的年际增量SH11、SH21、SH31、PSH11、PSH21, 然后再对这五个年际增量求相关。表 3给出了春季H3000上上述五个年际增量之间的相关系数。其中, PSH11与PSH21之间的相关系数为0.99, 这也进一步说明了密度对地表感热的年际增量变化影响较小。此外, SH11与SH31的相关系数高达0.86, 更加说明了61_站点地表感热与79_站点地表感热之间的年际增量密切相关, 表明61_站点资料是可用的。而且SH11与SH21的相关系数为0.54, 相较于SH1与SH2的0.27相关系数提高了很多, 说明即使热量拖曳系数计算方案不同, 但它们计算得到地表感热的年际增量相关程度依然较高。同样对春季H1500-2000、H2000-3000和夏季H1500-2000、H2000-3000以及H3000上的上述五个变量进行年际增量相关分析, 所得到的结论均与春季H3000上得到的结论一致。
| 表 3 春季青藏高原(海拔高于3 000 m)不同气象变量的年际增量和参数的相关系数 Table 3 The correlation coefficient between the year-to- year increment of different meteorological variables and parameters over the Qinghai-Tibetan Plateau (elevation over 3 000 m) in spring |
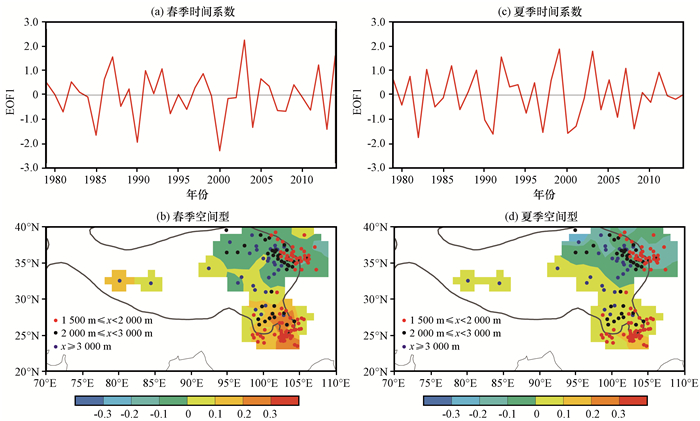
高原地表感热有很强的年际变化(张盈盈等, 2015), 不过在分析春夏两季年际地表感热的时空分布特征前, 有必要对地表感热的年际和年代际信号进行分离。对高原地表感热进行Lancos滤波, 得到2~9年年际信号后进行EOF分解(图 5)。图 5(b)给出的是1979-2014年高原79_站点春季年际地表感热EOF分解第一模态的空间分布形态, 其具有高原南北反向分布的特征, 南部有明显正中心, 该中心与春季地表感热大值中心相对应, 该模态所占方差贡献为18.1%。夏季年际地表感热第一模态空间型分布与春季相似, 同样是呈南北反向分布, 其所占方差贡献为14.8%[图 5(d)]。
|
图 5 1979-2014年青藏高原79_站点春季和夏季年际(2~9年)感热EOF第一模态时间系数以及空间型 灰色轮廓线是海拔为2 000 m的等值线 Figure 5 The time coefficient and the spatial distribution of the first leading mode of empirical orthogonal function analysis for spring and summer sensible heating in 79_ stations over the Qinghai-Tibetan Plateau on interannual time scale (2~9 years) during 1979-2014. Gray line indicates the elevation of 2 000 m |
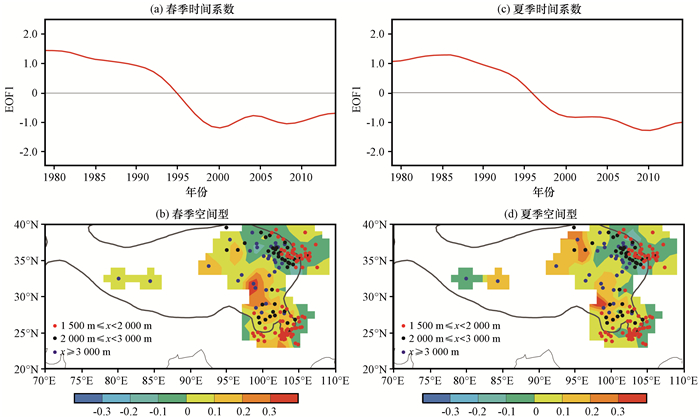
图 6与图 5类似, 给出的是1979-2014年高原79_站点春夏两季年代际(9年以上)地表感热EOF分解第一模态的空间分布形态及其时间系数。如图 6所示, 春季年代际地表感热第一模态空间型具有高原主体和其东北反向分布的特征, 所占方差贡献为44.4%。夏季年代际地表感热第一模态空间型与春季相似, 只是东北的负值区域范围更小, 所占方差贡献为41.3%。春夏两季EOF第一模态的时间系数均反映了年代际地表感热在高原主体从20世纪80年代到21世纪00年代有一个明显的减弱特征, 而高原东北部则与之相反。
|
图 6 1979-2014年青藏高原79_站点春季和夏季年代际(9年以上)感热EOF第一模态时间系数以及空间型灰色轮廓线是海拔为2 000 m的等值线 Figure 6 The time coefficient and the spatial distribution of the first leading mode of empirical orthogonal function analysis for spring and summer sensible heating in 79_ stations over the Qinghai-Tibetan Plateau on decadal time scale (above 9 years) during 1979-2014. Gray line indicates the elevation of 2 000 m |
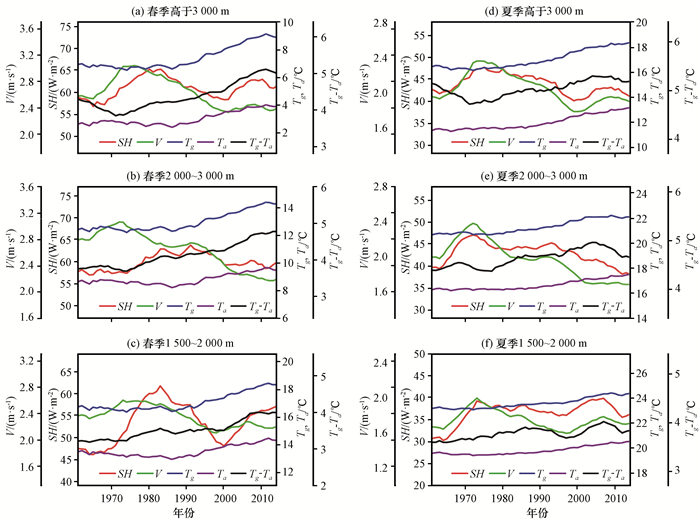
图 7给出了1961-2014年高原61_站点平均的春夏两季三种海拔上的SH、V、Tg、Ta以及Tg-Ta的9年滑动平均时间序列。如图 7所示, 平均而言, 春夏两季三种海拔上, SH在19611979年为上升趋势, 1979-2014年则呈现下降趋势, 且在1979-2003年间下降趋势更为显著, 与图 6和前人结果基本一致(Duan et al, 2008; Yang et al, 2011; Liu et al, 2012;王美蓉等, 2012)。20032014年春季H1500-2000和H3000为显著上升趋势, 夏季H2000-3000为显著下降趋势, 春季H2000-3000和夏季H1500-2000与H3000趋势不明显, 说明最近十几年高原地表感热在不同季节和不同高度上的变化是不一致的; V在19611975年为上升趋势, 19752014年则呈现下降趋势, 且在19752003年间下降趋势更为显著, 20032014年变化趋势不明显; Tg、Ta和Tg-Ta在19702010年为显著上升趋势。以上分析表明, 在V显著变化时期, SH与V的变化趋势是十分一致的。为了进一步定量地分析SH的变化趋势, 取1961-2014年、1979-2014年和减弱最显著的1979-2003年三个时段来进行分析。
|
图 7 1961-2014年青藏高原61_站点平均的SH、V、Tg、Ta以及Tg-Ta在春季和夏季不同海拔上的9年滑动平均时间序列 Figure 7 9-year running mean time series of 61_ stations average SH, V, Tg, Ta and Tg-Ta at different elevations over the Qinghai-Tibetan Plateau in spring and summer during 1961-2014 |
表 4显示了高原SH、V和Tg-Ta在春夏秋冬四季位于H1500-2000、H2000-3000和H3000三种海拔上的变化趋势。1961-2014年长时间上, SH的变化趋势除了在夏季H2000-3000和H3000上是显著减弱之外, 在其余所有季节和海拔上都是增加的。1979-2014年SH的变化趋势除了在秋冬两季H2000-3000上是微弱上升以外, 在其余所有季节和海拔上都是减弱的。
| 表 4 青藏高原SH(感热)变化趋势、V(风速)变化趋势和Tg-Ta(地气温差)变化趋势的季节海拔分布 Table 4 The trend of sensible heating, wind speed and ground-air temperature difference over the Qinghai-Tibetan Plateau in different seasons and at different elevations |
1979-2003年是SH显著减弱的时期。具体而言, 春秋冬三季减弱最显著的海拔均为H1500-2000, 变化率分别为-6.90、-2.82和-6.79 W·m-2·(10a)-1, 春冬两季在H2000-3000上减弱最不明显, 变化率分别为-2.35和-0.18 W·m-2·(10a)-1, 而秋季在H2000-3000上则呈现微弱的上升, 变化率为0.17 W·m-2·(10a)-1; 夏季减弱最显著的海拔为H3000, 变化率为-3.29 W·m-2·(10a)-1, 而在H1500-2000上减弱最不明显, 变化率为-0.26 W·m-2·(10a)-1。就高原整体而言, SH减弱趋势在春季最显著, 变化率为-4.55 W·m-2·(10a)-1, 冬秋两季次之, 变化率分别为-2.87和-1.67 W·m-2·(10a)-1, 夏季减弱最不明显, 变化率为-1.31 W·m-2·(10a)-1, 年平均变化率为-2.60 W·m-2·(10a)-1。而Duan et al(2008)利用高原中东部高于2 000 m的71站计算高原SH变化趋势, 得到春夏秋冬四季从大到小的减弱趋势依次为春季[-5.4 W·m-2·(10a)-1]、夏季[-3.1 W·m-2·(10a)-1]、秋季[-2.6 W·m-2·(10a)-1]和冬季[-2.3 W·m-2·(10a)-1], 年平均为-3.4 W·m-2·(10a)-1, SH减弱趋势比本文偏强。虽然减弱趋势均在春季最为显著, 但减弱最不明显的季节却不相同, 其原因主要是本文考虑了H1500-2000的SH变化趋势。如果只将本文H2000-3000和H3000两种海拔上的SH变化趋势做平均, 则得到春夏秋冬四季从大到小的减弱趋势依次为春季[-3.37 W·m-2·(10a)-1]、夏季[-1.84 W·m-2·(10a)-1]、秋季[-1.09 W·m-2·(10a)-1]和冬季[-0.92 W·m-2·(10a)-1], 此趋势的季节变化规律与Duan et al(2008)的研究结果一致。
综上所述, 1979-2003年, 春秋冬三季, SH变化趋势减弱最显著的海拔均为H1500-2000, 而在H2000-3000上, 春冬两季SH减弱最不明显, 秋季在此海拔上则是微弱的上升; 夏季SH变化趋势减弱最显著的海拔为H3000, 在H1500-2000减弱最不明显。就高原整体而言, SH减弱趋势在春季最为显著, 冬秋两季次之, 夏季减弱最不明显。
值得指出的是, Yang方案的地表感热通量年平均变化趋势计算结果比本文相较偏小, 但变化趋势一致, 不影响高原地表感热变化趋势呈持续减弱的结论。
由于密度对地表感热变率影响很小, 在热量拖曳系数取常数CHC的情况下, SH变化则由V和Tg-Ta的变化所决定。而在1979-2003年, SH是显著性减弱的, 那么V和Tg-Ta在此时段的变化趋势如何呢?
由表 4可知, 1979-2003年V在春夏秋冬四季H1500-2000、H2000-3000和H3000三种海拔上的变化趋势均是显著性减弱的, 减弱最显著的海拔为H3000, 在H1500-2000上减弱最弱; 而Tg-Ta在春夏秋三季H2000-3000和H3000以及冬季H3000上的变化趋势均是上升的, 但冬季H2000-3000以及春夏秋冬四季H1500-2000上的变化趋势却是减弱的, 这是导致SH减弱趋势在H1500-2000最为显著的一个重要原因。就高原整体而言, V在春夏秋冬四季均是减弱的, 与温度对全球变暖的区域响应不均匀有关(Duan et al, 2008; Liu et al, 2012)。高纬温度增加比在副热带大, 导致经向温度梯度和气压梯度减小, 从而使得风速减小。春季表面风速趋势减弱最为显著, 变化率为-0.29 m·s-1·(10a)-1, 秋季趋势减弱最不明显, 变化率为-0.14 m·s-1·(10a)-1。而Tg-Ta在春夏两季是上升的, 与Duan et al(2008)、Liu et al(2012)和王美蓉等(2012)研究结果相一致, 变化率均为0.07 ℃·(10a)-1, 在秋冬两季是减弱的, 与Duan et al(2008)的研究结果一致, 变化率分别为-0.01和-0.43 ℃·(10a)-1。
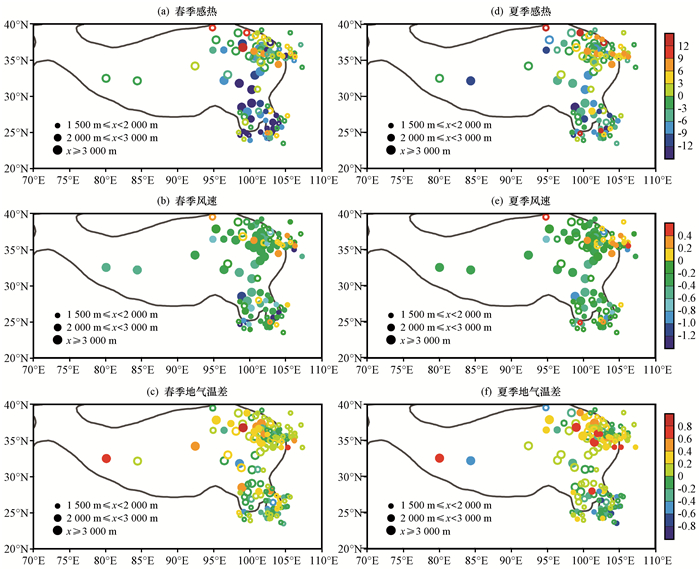
高原地形复杂, 天气气候局地特征显著。图 8给出了1979-2003年高原79_站点春夏两季SH趋势、V趋势和Tg-Ta趋势的空间分布。如图 8所示, 春季V为全区一致性的减弱, 南部比北部减弱更显著; 而Tg-Ta主要为北部上升南部减弱; SH则大致是全区一致性的减弱, 其中南部减弱更为显著。不过在北部有部分站点呈上升趋势, 这与该地区一些站点V增加且这些站点的Tg-Ta也是增加有关。夏季V趋势、Tg-Ta趋势和SH趋势的空间分布与春季基本一致, 不同的是高原南部V减弱趋势偏弱、北部Tg-Ta上升趋势偏强、全区SH减弱趋势偏弱。
|
图 8 1979-2003年青藏高原79_站点春季, 夏季感热趋势[单位: W·m-2·(10a)-1]、风速趋势[单位: m·s-1·(10a)-1]和地气温差趋势[单位: ℃·(10a)-1]的空间分布 灰色轮廓线是海拔为2 000 m的等值线, 实心点和空心点分别代表示通过和未通过95%信度检验的站点 Figure 8 The trend of sensible heating[unit: W·m-2·(10a)-1], wind speed[unit: m·s-1·(10a)-1] and ground-air temperature difference [unit: ℃·(10a)-1] in 79_ stations over the Qinghai-Tibetan Plateau in spring and summer during 1979-2003. Gray line indicates the elevation of 2 000 m. The dots with (without) shading are significant (insignificant) at the 95% confidence level |
本节首先比较年际和年代际时间尺度上地表感热方差的相对大小。表 5给出了1979-2014年高原79_站点在春夏秋冬四季H1500-2000、H2000-3000和H3000三种海拔上地表感热的年际和年代际方差贡献。如表 5所示, 在春夏两季H3000和春冬两季H1500-2000上地表感热的年际方差贡献为5.11~9.43 W2·m-4, 小于年代际方差贡献为5.37~24.27 W2·m-4, 其他的季节和海拔上年际方差贡献为4.06~6.97 W2·m-4, 大于年代际方差贡献0.88~4.91 W2·m-4。而且可以注意到, 在春冬两季H1500-2000上, 地表感热原始方差和年代际方差相比其他季节和海拔均显著偏大, 这是由于春季H1500-2000上地表感热的年代际变化显著, 即在19792002年为显著的减弱, 而在2002-2014年则为显著的上升[图 4(c)], 所以其年代际方差贡献非常大, 使得原始方差也显著偏大。冬季H1500-2000也是如此(图略)。
| 表 5 1979-2014年青藏高原79_站点感热年际(2~9年)和年代际(9年以上)方差贡献的季节海拔分布 Table 5 The interannual (2~9 years) and decadal (above 9 years) variance of sensible heating in 79_ stations over the Qinghai-Tibetan Plateau in different seasons and at different elevations during 1979-2014 |
由总体动力学公式[公式(1)]及前文可知, 干空气定压比热Cp为常数, 密度ρ对地表感热的变率影响很小, 在热量拖曳系数CH取为常值时, 地表感热的变化就由表面风速的变化和地气温差的变化共同决定。前人研究表面风速与地气温差对地表感热的相对贡献时, 大多都是定性的(Duan et al, 2008; Liu et al, 2012)。由于表面风速和地温、气温可能存在相互作用, 那么如何更准确的区分表面风速与地气温差对地表感热的相对贡献呢?研究表明, 偏相关方法能够基本剔除来自第三方因子的影响(Zar, 1999)。但相关系数只能说明两个变量的密切程度, 并不能表征在自变量变化幅度相同的情况下, 因变量的变化幅度。而因变量的变率可由多元线性标准化回归系数表示。标准化回归系数来自于多元线性回归方程中经过标准化的各自变量得到的回归系数。因此采用偏相关和多元线性回归两种方法来比较表面风速和地气温差与地表感热的密切程度。
表 6(表 7)给出了1979-2014年高原79_站点表面风速与地气温差在年际(年代际)时间尺度上对地表感热变化的相对贡献。以上三个变量均是做了年际(年代际)滤波后, 再进行偏相关[公式(3)]和多元线性回归[公式(4)]。表 6(表 7)中回归SH代表年际(年代际)时间尺度上表面风速与地气温差回归得到的地表感热, 而原始SH则是指经过年际(年代际)滤波后直接得到的地表感热。
| 表 6 1979-2014年青藏高原79_站点V(风速)与Tg-Ta(地气温差)在年际时间尺度上对SH(感热)变化相对贡献的季节海拔分布 Table 6 The relative contributions of wind speed and ground-air temperature difference to the variation of sensible heating on interannual time scale in 79_ stations over the Qinghai-Tibetan Plateau in different seasons and at different elevations during 1979-2014 |
| 表 7 1979-2014年青藏高原79_站点V(风速)与Tg-Ta(地气温差)在年代际时间尺度上对SH(感热)变化相对贡献的季节海拔分布 Table 7 The relative contributions of wind speed and ground-air temperature difference to the variation of sensible heating on decadal time scale in 79_ stations over the Qinghai-Tibetan Plateau in different seasons and at different elevations during 1979-2014 |
如表 6所示, 回归SH与原始SH的相关系数为0.62~0.98, 通过99%的信度检验, 而且所有回归方程均通过95%信度的F检验, 说明年际回归方程及其回归的地表感热是可信的。在春季H2000-3000与H3000、秋季H3000和冬季H1500-2000与H3000上V回归系数为0.58~1.00, 大于Tg-Ta回归系数0.44~0.58。而在表 6其他季节和海拔上, V回归系数为0.19~0.51, 小于Tg-Ta回归系数0.56~0.77。偏相关系数相比较得到的结论与回归系数相比较得到的结论一致。平均而言, 在年际时间尺度上, 表面风速对地表感热的贡献与地气温差对地表感热的贡献大小相当。
在年代际时间尺度上, 表 7中回归SH与原始SH的相关系数为0.47~0.97, 通过99%的信度检验, 而且所有回归方程均通过95%信度的F检验, 同样说明年代际回归方程及其回归的地表感热是可信的。冬季H2000-3000上V回归系数为0.01, 远小于Tg-Ta回归系数0.65, 说明此时地表感热的年代际变化由地气温差决定, 从9年滑动平均时间序列上也可以看出地表感热的走势与地气温差的走势基本一致(图略)。而在表 7其他季节和海拔上, V回归系数绝对值为0.51~1.32, 大于Tg-Ta回归系数绝对值0.13~0.98, 说明此时地表感热的年代际变化由表面风速决定。值得注意的是, 在秋季H2000-3000上V和Tg-Ta回归系数均为负值, 主要是因为此时的地表感热年代际信号特别弱, 其年代际方差贡献为0.88 W2·m-4, 对于原始方差5.70 W2·m-4来说可以忽略不计, 计算回归时容易出现误差。偏相关系数相比较得到的结论与回归系数相比较得到的结论一致, 在年代际时间尺度上, 表面风速对地表感热的贡献大于地气温差对地表感热的贡献, 与Duan et al(2008)和Liu et al(2012)的结果一致。
7 结论和讨论利用1961-2014年中国气象观测站点逐日常规资料, 分析了在不同季节和不同海拔上, 青藏高原地表感热的气候态特征以及热量拖曳系数和密度对地表感热计算的影响, 并研究了高原地表感热的年际、年代际以及趋势变化的时空分布特征, 最后结合偏相关和多元线性回归方法, 定量的研究了表面风速与地气温差在年际和年代际时间尺度上对地表感热变化的相对贡献。得到以下主要结论:
(1) 总体来说, 1979-2014年, 高原地表感热、表面风速以及地气温差随着高度上升而增加。季节变化上, 表面风速和地表感热均在春季最大秋季最小, 地表感热在冬季的值与秋季相当, 地气温差最大和最小值则分布于夏季和冬季; 空间分布上, 春季地表感热、表面风速和地气温差在高原东南部大北部小, 而夏季地表感热、表面风速和地气温差则是在高原南部小北部大。
(2) 不同密度计算方案对地表感热变率影响不大, 仅在量值上有细微差别。由不同热量拖曳系数计算方案得到两种地表感热的线性相关程度不高, 但是它们的年际增量密切相关, 在1979-2003年间两者的变化趋势呈现相反的特征。当密度由干空气状态方程决定, 而热量拖曳系数取为常数时, 此方案计得的地表感热能够更加合理地表征地表感热特征。1979-2014年, 春夏两季:年际地表感热EOF第一模态空间型均具有高原南北反向分布的特征, 春季南部有明显正中心, 该中心与春季地表感热大值中心相对应; 而年代际地表感热EOF第一模态空间型均具有高原主体和其东北反向分布的特征, 但夏季高原东北部的负值区域范围比春季小, 第一模态的时间系数均反映了年代际地表感热在高原主体从20世纪80年代到21世纪00年代显著减弱, 而高原东北部与之相反。
(3) 平均而言, 在较长时期, 地表感热在19611979年呈上升趋势; 在1979-2003年呈减弱趋势, 而在20032014年又为上升趋势。在显著下降的1979-2003年, 春秋冬三季, 地表感热均在1 500~2 000 m减弱最强, 对应表面风速变化, 夏季地表感热在高于3 000 m减弱最强, 而在1 500~2 000 m减弱最弱; 一年四季, 表面风速在高于3 000 m有最显著的减弱趋势, 而地气温差在高于2 000 m呈上升趋势, 2 000 m以下则呈减弱趋势。春秋冬三季, 地气温差的变化趋势是导致地表感热在1 500~2 000 m减弱最显著的一个重要原因。就高原整体而言, 春季地表感热减弱趋势最强, 冬秋次之, 夏季最弱; 春季表面风速减弱趋势也是最强, 冬季和夏季紧随其后, 秋季最弱; 而地气温差在秋冬两季为减弱趋势, 在春夏两季呈上升趋势。空间上, 春季地表感热、表面风速和地气温差的变化趋势分布与夏季大体一致:地表感热和表面风速基本为高原全区一致性的减弱, 不过南部减弱更显著; 而地气温差主要为北部上升, 南部减弱。
(4) 总体而言, 1979-2014年, 在春夏两季高于3 000 m和春冬两季1 500~2 000 m上地表感热的年际方差贡献小于年代际方差贡献, 而在其他的季节和海拔上年际方差贡献大于年代际方差贡献。在年际时间尺度上, 表面风速对地表感热的贡献与地气温差对地表感热的贡献大小相当; 而在年代际时间尺度上, 表面风速对地表感热的贡献大于地气温差对地表感热的贡献。
本文分析了地表感热、表面风速和地气温差在一年四季的1 500~2 000 m、2000~3 000 m和高于3 000 m三种海拔上的气候态特征和它们的年际、年代际以及趋势变化特征。这些特征与环流的联系, 还需进一步研究。
Chen L X, Reiter E R, Feng Z Q. 1985. The atmospheric heat source over the Tibetan Plateau:May-August 1979[J]. Mon Wea Rev, 113(10): 1771–1790.
DOI:10.1175/1520-0493(1985)113<1771:TAHSOT>2.0.CO;2 |
|
Duan A M, Wang M R, Lei Y H, et al. 2013. Trends in summer rainfall over China Associated with the Tibetan Plateau sensible heat source during 1980-2008[J]. J Climate, 26(1): 261–275.
DOI:10.1175/JCLI-D-11-00669.1 |
|
Duan A M, Wang M R, Xiao Z X. 2014. Uncertainties in quantitatively estimating the atmospheric heat source over the Tibetan Plateau[J]. Atmos Oceanic Sci Lett, 7(1): 28–33.
DOI:10.1080/16742834.2014.11447131 |
|
Duan A M, Wu G X. 2008. Weakening trend in the atmospheric heat source over the Tibetan Plateau during recent decades.Part Ⅰ:Observations[J]. J Climate, 21(13): 3149–3164.
DOI:10.1175/2007JCLI1912.1 |
|
Fan K, Wang H J, Choi Y J. 2008. A physically-based statistical forecast model for the middle-lower reaches of the Yangtze River Valley summer rainfall[J]. China Sci Bull, 53(4): 602–609.
DOI:10.1007/s11434-008-0083-1 |
|
Flohn H. 1957. Large-scale aspects of the "summer monsoon" in South and East Asia[J]. J Meteor Soc Japan, 75: 180–186.
DOI:10.2151/jmsj1923.35A.0_180 |
|
He H Y, McGinnis J W, Song Z S, et al. 1987. Onset of the Asian summer monsoon in 1979 and the effect of the Tibetan Plateau[J]. Mon Wea Rev, 115(115): 1966–1995.
|
|
Li C F, Yanai M. 1996. The onset and interannual variability of the Asian summer monsoon in relation to land-sea thermal contrast[J]. J Climate, 9(2): 358–375.
DOI:10.1175/1520-0442(1996)009<0358:TOAIVO>2.0.CO;2 |
|
Liu Y M, Hoskins B, Blackburn M. 2007. Impact of Tibetan orography and heating on the summer flow over Asia[J]. J Meteor Soc Japan, 85(7): 1–19.
|
|
Liu Y M, Wu G X, Hong J L, et al. 2012. Revisiting Asian monsoon formation and change associated with Tibetan Plateau forcing:Ⅱ.Change[J]. Climate Dyn, 39(5): 1183–1195.
DOI:10.1007/s00382-012-1335-y |
|
Molnar P, Emanuel K A. 1999. Temperature profiles in radiative-convective equilibrium above surfaces at different heights[J]. J Geophys Res, 104(D20): 24265–24271.
DOI:10.1029/1999JD900485 |
|
Qian Y F, Zhang Y, Huang Y Y, et al. 2004. The effects of the thermal anomalies over the Tibetan Plateau and its vicinities on climate variability in China[J]. Adv Atmos Sci, 21(3): 369–381.
DOI:10.1007/BF02915565 |
|
Wu G X, He B, Duan A M, et al. 2017. Formation and variation of the atmospheric heat source over the Tibetan Plateau and its climate effects[J]. Adv Atmos Sci, 34(10): 1169–1184.
DOI:10.1007/s00376-017-7014-5 |
|
Wu G X, Liu Y M, Dong B W, et al. 2012. Revisiting Asian monsoon formation and change associated with Tibetan Plateau forcing:Ⅰ.Formation[J]. Clim Dyn, 39(5): 1169–1181.
DOI:10.1007/s00382-012-1334-z |
|
Wu G X, Liu Y M, Wang T M, et al. 2007. The influence of the mechanical and thermal forcing of the Tibetan Plateau on the Asian climate[J]. J Hydrometeorol, 8(4): 770–789.
DOI:10.1175/JHM609.1 |
|
Wu G X, Zhang Y S. 1998. Tibetan Plateau forcing and timing of the monsoon onset over South Asia and South China Sea[J]. Mon Wea Rev, 126(4): 913–927.
DOI:10.1175/1520-0493(1998)126<0913:TPFATT>2.0.CO;2 |
|
Yanai M, Li C F, Song Z S. 1992. Seasonal heating of the Tibetan Plateau and its effects on the evolution of the Asian summer monsoon[J]. J Meteor Soc Japan, 79(1): 319–351.
|
|
Yang K, Guo X F, Wu B Y. 2011. Recent trends in surface sensible heat flux on the Tibetan Plateau[J]. Sci China Earth Sci, 54(1): 19–28.
DOI:10.1007/s11430-010-4036-6 |
|
Yang K, Qin J, Guo X F, et al. 2009. Method development for estimating sensible heat flux over the Tibetan Plateau from CMA Data[J]. J Appl Meteor Climatol, 48(12): 2474–2486.
DOI:10.1175/2009JAMC2167.1 |
|
Yang K, Wu H, Qin J, et al. 2014. Recent climate changes over the Tibetan Plateau and their impacts on energy and water cycle:A review[J]. Global & Planetary Change, 112(1): 79–91.
|
|
Ye D Z, Wu G X. 1998. The role of the heat source of the Tibetan Plateau in the general circulation[J]. Meteor Atmos Phys, 67(1/4): 181–198.
|
|
Zar H J, 1999.Biostatistical Analysis, fourth ed[C].Pearson Education, New Jersey.
|
|
Zhu X Y, Liu Y M, Wu G X. 2012. An assessment of summer sensible heat flux on the Tibetan Plateau from eight data sets[J]. Sci China Earth Sci, 55(5): 779–786.
DOI:10.1007/s11430-012-4379-2 |
|
陈隆勋, 朱乾根, 罗会邦, 等. 1991. 东亚季风[M]. 北京: 气象出版社.
Chen L X, Zhu Q G, Luo H B, et al. 1991. East Asian Monsoon[M]. Beijing: China Meteorological Press.
|
|
陈万隆, 翁笃鸣, 1984.关于青藏高原感热和潜热旬总量计算方法的初步研究//青藏高原气象科学实验论文集(二)[C].北京: 科学出版社, 35-45.
Chen W L, Wong D M, 1984.A preliminary study on the computational method of 10-day mean sensible heat and latent heat on the Tibetan Plateau.Collected Works of the Qinghai-Xizang Plateau Meteorological Experiment (Series 2)[C].Beijing: Science Press, 35-45.
|
|
李国平, 段廷扬, 巩远发. 2000. 青藏高原西部地区的总体输送系数和地面通量[J]. 科学通报, 45(8): 865–869.
Li G P, Duan T Y, Gong Y F. 2000. The bulk transfer coefficients and surface fluxes on the western Tibetan Plateau[J]. Chinese Sci Bull, 45(8): 865–869.
DOI:10.3321/j.issn:0023-074X.2000.08.015 |
|
刘屹岷, 王子谦, 卓海峰, 等. 2017. 夏季亚洲大地形双加热及近对流层顶位涡强迫的激发Ⅱ:伊朗高原-青藏高原感热加热[J]. 中国科学:地球科学, 47: 354–366.
Liu Y M, Wang Z Q, Zhuo H F, et al. 2017. Two types of summertime heating over Asian large-scale orography and excitation of potential-vorticity forcing Ⅱ.Sensible heating over Tibetan-Iranian Plateau[J]. Sci China Earth Sci, 47: 354–366.
DOI:10.1007/s11430-016-9016-3 |
|
庞轶舒, 马振峰, 杨淑群, 等. 2017. 盛夏高原季风指数的探讨及其对四川盆地降水的影响[J]. 高原气象, 36(4): 886–899.
Pang Y S, Ma Z F, Yang S Q, et al. 2017. Discussion of plateau monsoon index and its impact on precipitation in Sichuan Basin in midsummer[J]. Plateau Meteor, 36(4): 886–899.
DOI:10.7522/j.issn.1000-0534.2016.00027 |
|
任芝花, 余予, 邹凤玲, 等. 2012. 部分地面要素历史基础气象资料质量检测[J]. 应用气象学报, 23(6): 739–747.
Ren Z H, Yu Y, Zou F L, et al. 2012. Quality detection of surface historical basic meteorological data[J]. J Appl Meteor Sci, 23(6): 739–747.
DOI:10.3969/j.issn.1001-7313.2012.06.011 |
|
王慧, 李栋梁. 2010. 卫星遥感结合地面观测资料对中国西北干旱区地表热力输送系数的估算[J]. 大气科学, 34(5): 1026–1034.
Wang H, Li D L. 2010. Estimation of the surface thermal transfer coefficients over the arid region of Northwest China with the aid of satellite remote sensing an d field observations[J]. Chinese J Atmos Sci, 34(5): 1026–1034.
DOI:10.3878/j.issn.1006-9895.2010.05.16 |
|
王美蓉, 周顺武, 段安民. 2012. 近30年青藏高原中东部大气热源变化趋势:观测与再分析资料对比[J]. 科学通报, 57(Z1): 178–188.
Wang M R, Zhou S W, Duan A M. 2012. Trend in the atmospheric heat source over the central and eastern Tibetan Plateau during recent decades:Comparison of observations and reanalysis data[J]. Chinese Sci Bull, 57(Z1): 178–188.
|
|
王顺久. 2017. 青藏高原积雪变化及其对中国水资源系统影响研究进展[J]. 高原气象, 36(5): 1153–1164.
Wang S J. 2017. Progresses in variability of snow cover over the Qinghai-Tibetan Plateau and its impact on water resources in China[J]. Plateau Meteor, 36(5): 1153–1164.
DOI:10.7522/j.issn.1000-0534.2016.00117 |
|
吴国雄, 李伟平, 郭华, 等, 1997.青藏高原感热气泵和亚洲夏季风//叶笃正.赵九章纪念文集[C].北京: 科学出版社, 116-126.
Wu G X, Li W P, Guo H, et al, 1997.Sensible heat driven air-pump over the Tibetan Plateau and its impacts on the Asian summer monsoon//Ye D Z.Essays in Honor Zhao Jiuzhang[C].Beijing: Chinese Science Press, 116-126.
|
|
吴国雄, 卓海峰, 王子谦, 等. 2016. 夏季亚洲大地形双加热及近对流层顶位涡强迫的激发(Ⅰ):青藏高原主体加热[J]. 中国科学:地球科学, 46: 1209–1222.
Wu G X, Zhuo H F, Wang Z Q, et al. 2016. Two types of summertime heating over the Asian large-scale orography and excitation of potential-vorticity forcing (Ⅰ).Over Tibetan Plateau[J]. Sci China Earth Sci, 46: 1209–1222.
DOI:10.1007/s11430-016-5328-2 |
|
杨智, 刘志刚, 李娟. 2010. 云南省地气温差时空变化特征分析[J]. 云南大学学报, 32(S1): 289–293.
Yang Z, Liu Z G, Li J. 2010. The characteristic of temporal and spatial distribution of the differences between ground and air temperature in Yunnan[J]. Journal of Yunnan University, 32(S1): 289–293.
|
|
叶笃正, 高由禧. 1979. 青藏高原气象学[M]. 北京: 科学出版社, 329-337.
Ye D Z, Gao Y X. 1979. The Meteorology of the Qinghai-Xizang (Tibet) Plateau[M]. Beijing: Science Press, 329-337.
|
|
张文纲, 李述训, 吴通华, 等. 2006. 青藏高原地气温差变化分析[J]. 地理学报, 61(9): 899–910.
Zhang W G, Li S X, Wu T H, et al. 2006. Changes of the Differences between Ground and Air Temperature over the Qinghai-Xizang Plateau[J]. Acta Geophys Sinica, 61(9): 899–910.
DOI:10.3321/j.issn:0375-5444.2006.09.001 |
|
张盈盈, 李忠贤, 刘伯奇. 2015. 春季青藏高原表面感热加热的年际变化特征及其对印度夏季风爆发时间的影响[J]. 大气科学, 39(6): 1059–1072.
Zhang Y Y, Li Z X, Liu B Q. 2015. Interannual variability of surface sensible heating over the Tibetan Plateau in boreal spring and its influence on the onset time of the Indian Summer Monsoon[J]. Chinese J Atmos Sci, 39(6): 1059–1072.
|
|
张长灿, 李栋梁, 王慧, 等. 2017. 青藏高原春季地表感热特征及其对中国东部夏季雨型的影响[J]. 高原气象, 36(1): 13–23.
Zhang C C, Li D L, Wang H, et al. 2017. Characteristics of the surface sensible heat on the Qinghai-Xizang Plateau in the spring and its influences on the summertime rainfall pattern over the Eastern China[J]. Plateau Meteor, 36(1): 13–23.
DOI:10.7522/j.issn.1000-0534.2016.00028 |
|
周俊前, 刘新, 李伟平, 等. 2016. 青藏高原春季地表感热异常对西北地区东部降水变化的影响[J]. 高原气象, 35(4): 845–853.
Zhou J Q, Liu X, Li W P, et al. 2016. Relationship between surface sensible heating over the Qinghai-Xizang Plateau and precipitation in the eastern part of Northwest China in spring[J]. Plateau Meteor, 35(4): 845–853.
DOI:10.7522/j.issn.1000-0534.2015.00053 |
|
卓嘎, 德吉卓玛, 尼玛吉. 2017. 青藏高原土壤湿度分布特征及其对长江中下游6、7月降水的影响[J]. 高原气象, 36(3): 657–666.
Zhuo G, Deji Z M, Nima J. 2017. Distribution of soil moisture over the Qinghai-Tibetan Plateau and its effect on the precipitation in June and July over the mid-lower reaches of Yangtze River Basin[J]. Plateau Meteor, 36(3): 657–666.
DOI:10.7522/j.issn.1000-0534.2016.00073 |
2. State Key Laboratory of Numerical Modelling for Atmospheric Sciences and Geophysical Fluid Dynamics, Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
 2018, Vol. 37
2018, Vol. 37
