风能是一种清洁、可再生、储量巨大的能源, 风电装机容量呈“井喷式”不断增长。据全球风能理事会预测到2020年风电年新增市场将达到100 GW, 累计市场达到879 GW; 2015年, 中国风电新增装机容量30.5 GW, 同比上升26.61%;然而, 风速的不稳定性、随机性特征使风电场接入电网时电力运行系统的不确定性因素增多(孙丹, 2015; 张双益等, 2017), 客观上增加了电力调度、电网安全稳定运行的压力和挑战, 加之全国电力需求放缓、风电本地消纳不足等因素使得弃风限电形势加剧, 平均弃风率达15%, 其中甘肃省弃风率达39%, 弃风电量达82亿千瓦时(沈德昌, 2015)。因此准确的风速预报能够尽可能真实地反应风电功率的波动性和随机性, 是提高调度运行水平和有效增强甘肃省风电消纳能力的重要措施之一。目前近地层风速预报手段主要基于数值模式。复杂地形下的近地面边界层风场日变化有显著的山谷风特征, 随高度增加, 风速和风向变化明显(李晓霞, 2017; 曹杨, 2017)。张飞民等(2014)和Wang et al(2014)利用WRF-3DVAR同化常规观测资料可以使模式各垂直层上的合成风速及温度更加接近观测场, 尤其对近地层风速的改进较为明显。孙金学等(2017)指出WRF-LES通过对大气边界层内大尺度湍涡的直接解析, 可以体现出近地层风场的高度起伏性, 从而提高数值模拟的真实性和准确性。石岚等(2017)基于ECMWF集合风速预报产品和风能专业数值模式预报产品, 通过多统计量融合, 提取波动风速的概率信息, 对最有可能的风速波动位置进行预报, 发现融合预报对提升现有数值预报产品的精度有明显的改进。但是数值模式仍存在局限:难以精确描述大气运动的所有物理过程、次网格参数化过程中不能考虑大尺度对小尺度的影响及其反馈作用、初始场误差难以避免等因素导致数值预报误差始终存在(张兰慧等, 2011)。国内外学者大多数采用MOS、PP等统计方法对风速等预报产品进行误差订正。Marzban et al(1998)应用人工神经网络方法对数值模式预报的气象要素场进行订正, 订正后有效提高了数值模式对各气象要素的预报精度。余江等(2015)以内蒙古某风电场为试点, 在WRF模式的基础上分别结合持续法、时间序列法建立了风电场的短期风速预报方法, 为风电场短期风速预报精度的进一步提高提供了技术方法。卡尔曼滤波方法在预测风速递推滚动订正的过程中能够不断更新实际观测的风速信息, 不断滚动修正风速数据的状态。另外, 卡尔曼滤波订正方法对于新建的风电场数据资料长度有限的情况下, 可以有效克服少量训练样本难以取得较好订正效果的局限性。本文以典型风电场(南湫、黑崖子和干河口)为研究对象, 选取2016年测风塔70 m高度的实况风速、风机机头的风速、BJ-RUC数值模式的预报风速、气压等数值预报产品数据开展相关研究。
2 资料选取和方法介绍 2.1 资料选取所用资料包括: (1)2016年112月南湫、黑崖子、干河口风电场数值模式BJ-RUC的70 m预报产品数据(包括风速、压强等), 模式预报区域为96.45°E127.53°E, 37.20°N54.48°N, 垂直方向共38层, 顶层为50 hPa, 西北地区产品空间分辨率为9 km, 时间分辨率为15 min; (2)南湫、黑崖子和干河口风电场2016年112月的典型样板风机机头实况风速, 时间分辨率为5 min, 资料完整性达95%以上; (3)测风塔70 m高度层的风速、风向数据(若70 m数据存在缺测情况, 则用50 m高度层的数据资料填补)。
2.2 方法介绍卡尔曼滤波的量测方程为
| $ {Y_t} = {X_t}{\beta _t} + {e_t}, $ | (1) |
式中: Yt=[y1, y2, y3, …, yn]T为n维量测变量(预报量); Xt为预报因子矩阵:
| $ {X_t} = {\left[ {\begin{array}{*{20}{c}} {{x_{11}}}&{{x_{12}}}& \cdots &{{x_{1m}}} \\ {{x_{21}}}&{{x_{22}}}& \cdots &{{x_{2m}}} \\ \cdots&\cdots&\cdots&\cdots \\ {{x_{n1}}}&{{x_{n2}}}& \cdots &{{x_{nm}}} \end{array}} \right]_t}, $ | (2) |
βt=[β1, β2, …, βm]tT为因子的系数, 即卡尔曼滤波订正模型的状态向量; et为量测噪声, 是n维随机向量。βt作为卡尔曼滤波模型的状态向量, 可用状态方程描述其变化:
| $ {\beta _t} = {\mathit{\Phi} _{t - 1}}{\beta _{t - 1}} + {\varepsilon _{t - 1}}, $ | (3) |
其中: Φt-1为状态转移矩阵; εt-1为动态噪声, 是m维随机向量。如果假定状态向量βt随时间变化是渐进的, 作为一种近似, 可以假定Φt-1为单位矩阵(孔玉寿等, 2010)。因此在本文中状态向量可以简化为:
| $ {\beta _t} = {\beta _t} + {\varepsilon _{t - 1}}. $ | (4) |
从t-1时刻到t时刻的过程中, 因受到动态噪声εt-1影响, 状态向量由βt-1变化到βt。
采用的卡尔曼滤波滚动订正递推方程组为:
| $ {\hat Y_t} = {X_t}{\hat \beta _{t - 1}}, $ | (5) |
| $ {R_t} = {C_{t - 1}} + W, $ | (6) |
| $ {\sigma _t} = {X_t}{R_t}X_t^T + V, $ | (7) |
| $ {A_t} = {R_t}X_t^T\sigma _t^{ - 1}, $ | (8) |
| $ {\hat \beta _t} = {\hat \beta _{t - 1}} + {A_t}\left({{Y_t} - {{\hat Y}_t}} \right), $ | (9) |
| $ {C_t} = {R_t} - {A_t}{\sigma _t}A_t^T, $ | (10) |
公式(5)~(10)组成风速滚动订正的核心递推系统, 其中:
祝赢等(2013)和陆如华等(1997)的研究表明, 在剔除相关性较小的垂直风速、湿度等预报因子建立卡尔曼滤波订正模型时, 能够有效地降低预报方程的阶数, 并且订正效果比较显著。比较9月黑崖子、南湫和干河口风电场(分别由HYZ、HXNQ、GHK代表, 下同)典型样板机机头的观测风速和BJ-RUC数值模式预报产品的相关系数(表 1)可知, 预报风速与机头风速相关系数最大; 其次为预报气压, 与机头风速呈负相关, 相对于温度等因子, 相关性较高。因此选取历史观测和预报的风速、气压数据作为预报因子, 建立回归方程, 并根据所建立的回归方程确立卡尔曼滤波订正模型参数的初值(状态向量、误差矩阵、对角矩阵、量测噪声方阵)。
| 表 1 典型风电场样板风机机头观测风速与预报要素的相关性 Table 1 Correlations between observed wind speed and prediction elements of sample fans on typical wind farms |
根据选取订正时刻前14天的样本资料计算卡尔曼滤波订正模型的状态向量, 例如黑崖子风电场1#风机的样本数据计算出的状态向量初值β0为:
| $ {\beta _0} = {\left[ {\begin{array}{*{20}{c}} { - 132.\;04}&{10.\;45}&{1.\;70} \end{array}} \right]^T}. $ | (11) |
由于β0是由样本资料计算得来, 并且假定状态向量β0是比较准确的, 可认为误差方差阵C0是零矩阵, 即:
| $ {C_0} = {\left[ 0 \right]_{3 \times 3}}. $ | (12) |
W是输入噪声的方差阵, 根据白噪声的假定, W为对角矩阵, 可用β变化来估算, 计算公式为:
| $ W \approx \left[ {\begin{array}{*{20}{c}} {{{\left({\Delta {\beta _1}} \right)}^2}/\Delta T}&0&0 \\ 0&{{{\left({\Delta {\beta _2}} \right)}^2}/\Delta T}&0 \\ 0&0&{{{\left({\Delta {\beta _3}} \right)}^2}/\Delta T} \end{array}} \right]. $ | (13) |
V为量测噪声方阵, 由于Y的分量只有一个, 因此量测噪声方阵的可以通过公式(14)计算:
| $ V = Q/\left({k - m - 1} \right), $ | (14) |
式中: Q为回归系数β0回归方程的残差平方和; k为样本容量; m为预报因子的个数。
2.3 订正误差评价方法采用统计指标参数相关系数、平均绝对误差、均方根误差评价数值模式预报风速订正前后的误差, 即:
| $ \sigma = \frac{{\sum\nolimits_{i = 1}^N {\left({{X_i} - \bar X} \right)\left({{Y_i} - \bar Y} \right)} }}{{\sqrt {\sum\nolimits_{i = 1}^N {{{\left({{X_i} - \bar X} \right)}^2}} \sum\nolimits_{i = 1}^N {{{\left({{Y_i} - \bar Y} \right)}^2}} } }}, $ | (15) |
| $ MAE = \frac{1}{N}\sum\limits_{i = 1}^N {\left| {Y_o^i - Y_f^i} \right|}, $ | (16) |
| $ RMSE = \sqrt {\frac{{\sum\nolimits_{i = 1}^N {{{\left({Y_o^i - Y_f^i} \right)}^2}} }}{N}}, $ | (17) |
式中:
地形、季节是影响准确预报风速的关键因素(黄凤新, 2013)。通过公式(18)计算平均风速
| $ \overline {{V_E}} = \frac{1}{n}\sum\nolimits_{i = 1}^n {{V_i}}, $ | (18) |
式中: Vi为风速观测序列; n为平均风速计算时段内(年、月)的风速序列样本数。
假定风机的切入风速3 m·s-1, 切出风速25 m·s-1, 3~25 m·s-1为有效风速段。南湫、黑崖子和干河口风电场的有效风速时数占全年风速时数的百分比分别达90.9%, 85.06%和82.93%。各风电场有效风速时数存在显著的时间差异:南湫风电场有效风速时数百分比秋季最大, 达29.65%;其次为冬季(28.29%), 夏季次之(16.94%)。黑崖子风电场有效风速时数百分比夏季最大, 达27.19%;其次为春季(24.74%), 冬季次之(18.45%)。干河口夏季风况最好, 有效风速时数百分比达23.24%;秋冬季接近, 约达21%, 冬季有效风时数最少, 达18.8%。
从各风电场测风塔70 m高度层风速的夏、秋季日变化(图 1)中可以看出, 南湫风电场6月份风速呈现出多峰多谷的变化特征, 在12:00(北京时, 下同)左右达到最强盛阶段; 78月风速日变化则趋向双峰双谷分布, 峰值主要出现在午后和凌晨; 秋季, 910月风速由双峰双谷的变化趋势逐渐过渡为多波动性变化特征(11月)。黑崖子风电场风速具有显著的日变化特征, 68月风速逐时变化趋势相近, 呈单峰单谷分布特征。夏季风速极小值一般出现在06:00左右, 可达5.66 m·s-1; 即低谷之后风速呈上升趋势, 峰值一般出现在午后, 最大可达9.92 m·s-1。秋季风速呈多波动特征, 仍在午后出现峰值。干河口风电场67月风速变化特征相似, 呈双峰单谷的变化特征, 但是与南湫、黑崖子风电场风速变化相比, 干河口风速的波动性和随机性特征更加显著(后文做进一步说明)。
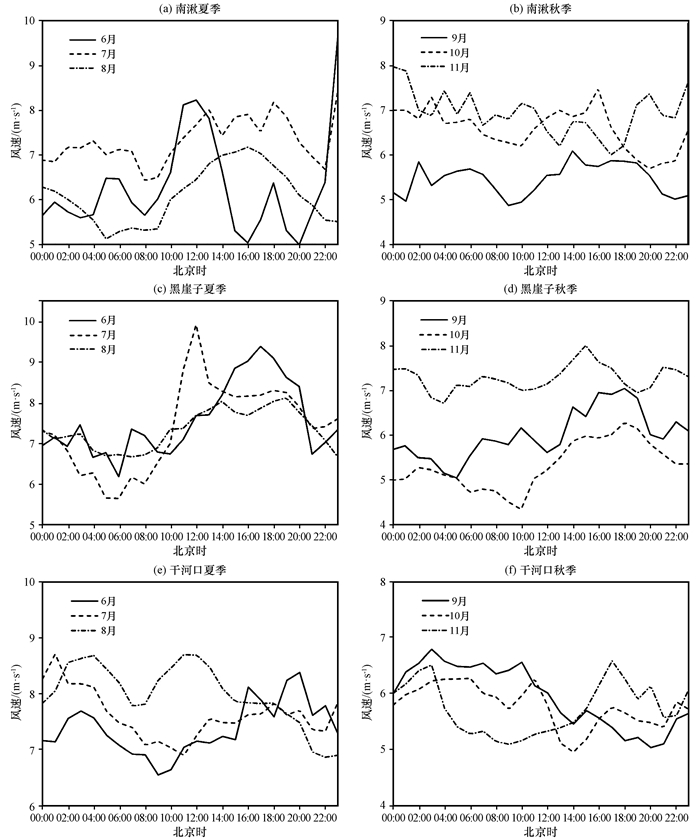
|
图 1 2016年南湫、黑崖子和干河口风电场夏季和秋季测风塔风速的日变化特征 Figure 1 The diurnal variation of wind speed at wind towers of Nanqiu, Heiyazi and Ganhekou in summer and autumn of 2016 |
通过对各风电场有效风速时数相对较大的夏、秋季的风向、风速做统计, 得到测风塔70 m高度层的风向频率和风速玫瑰图(图 2)。从图 2中可以看出, 南湫风电场夏、秋季盛行东南风, 其次为西北风; 夏季东南风发生频率最大, 达44.68%。黑崖子风电场夏、秋季节风向有明显的季节性转变, 夏到秋季由偏东风转换为偏西风。干河口风电场风向比较稳定, 夏到秋季主导风向持续为东风或偏东风, 风向发生频率分别为62.31%和55.68%。
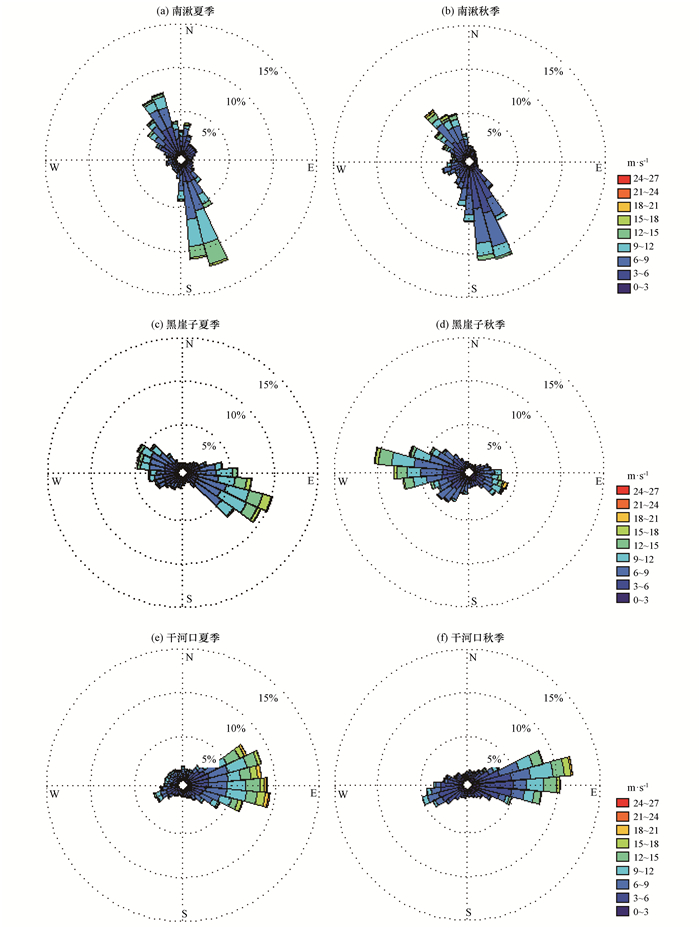
|
图 2 2016年南湫、黑崖子和干河口风电场夏季和秋季测风塔风向频率和风速玫瑰图 Figure 2 The frequency of wind direction and wind rose diagrams of Nanqiu, Heiyazi and Ganhekou in summer and autumn in 2016 |
风速具有较强的波动性和随机性特征, 一般情况下其概率分布呈偏正态分布。姜广绪等(2015)、Conradsen et al(1984)和龚伟俊等(2011)指出威布尔分布能够在复杂地形中有效并且较为准确地描述风速和评估风能。严彦等(2011)的研究表明, 测风数据在较短时间间隔的情况下, 采用平均风速和标准差估算威布尔分布参数具有较高的精度。采用平均风速和标准差估计威布尔分布的形状参数K和尺度参数C, 其中形状参数K与平均风速的变化程度有关, K值越大, 风速变化越小(即阵性越弱); 反之K值越小, 风速变化越大(即阵性越强); 尺度参数C与风速平均值有关, C值越大表明风速平均值越大。
图 3为2016年6月和9月各风电场预报风速和实况风速的威布尔概率分布及风速频数统计, 对应的在表 2中统计实况风速、预测风速、订正风速的威布尔分布形状参数和尺度参数。南湫风电场预测风速分布曲线相对实况风速分布曲线偏右[图 3(a), (b)]; 6月和9月, 实况风速威布尔分布形状参数(K-ob)分别为1.9和2.11(表 2), 说明6月比9月风速阵性强; 预测风速的威布尔分布形状参数(K-pre)分别为2.25和2.86, 均大于实况风速的威布尔分布形状参数; 6月和9月南湫风电场预报风速的尺度参数(C-pre)分别为7.86和5.94, 而实况风速的威布尔分布尺度参数(C-ob)较小, 6月和9月分别达4.65和5.85, 说明预报风速的平均值较实况风速的平均值偏大, 后文通过对比实况风速的威布尔分布参数和订正风速的威布尔分布形状参数(K-cor)和尺度参数(C-cor)来说明订正效果。同样, 从6月和9月黑崖子风电场风速的威布尔概率分布曲线来看, 预测风速的分布曲线仍然偏右, 且9月的偏差程度比6月大[图 3(c), (d)]; 对应时段内, 黑崖子风电场预报风速威布尔分布的形状参数和尺度参数均大于实况风速的分布参数(表 2)。图 3(e)和3(f)显示, 干河口风电场6月实况风速威布尔分布形状参数和尺度参数分别为1.33和4.65, 而预测风速威布尔分布形状参数和尺度参数分别为1.64和5.85, 预测风速概率分布曲线仍呈偏右分布, 但形状参数接近(均小于2), 说明相对于南湫、黑崖子风电场预报风速的阵性变化而言, 数值模式对干河口风速强阵性变化模拟较好。对比各风电场预测风速和观测的频数分布(图 3)发现, 9月南湫、黑崖子、干河口风电场观测风速出现最大频数的风速段分别为4~5, 4~5和2~3 m·s-1, 而预测风速的最大频数的风速段分别为6~7, 6~8和2~3 m·s-1, 这也可以说明南湫和黑崖子风电场预测风速相对实况风速偏大。
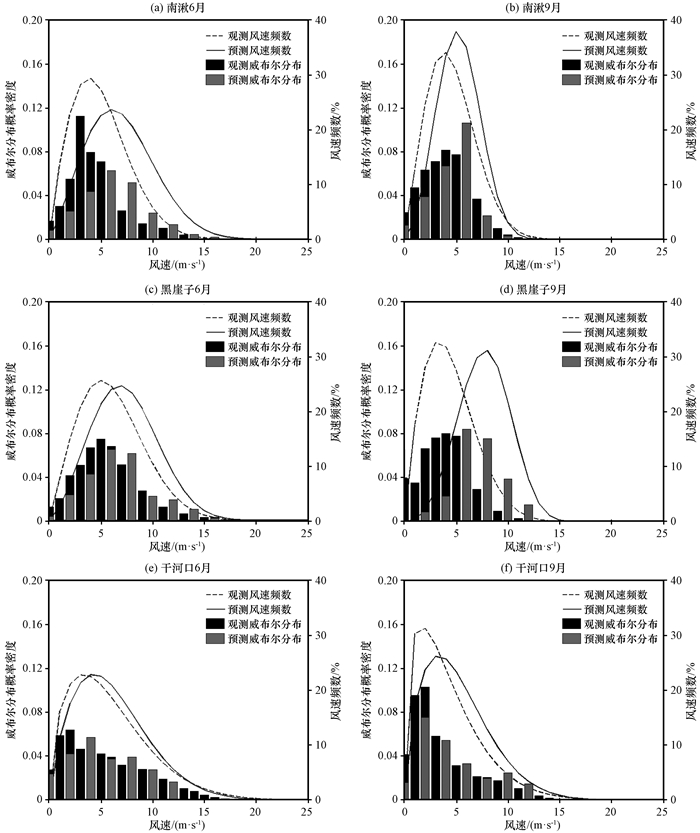
|
图 3 南湫、黑崖子和干河口风电场2016年6月和9月预报和实况风速的威布尔分布及风速频数对比 Figure 3 The comparison between Weibull distributions and frequency of forecast wind speed and observed wind speed of Nanqiu, Heiyazi and Ganhekou in June and September in 2016 |
| 表 2 典型风电场风速威布尔分布的无量纲参数统计 Table 2 Statistics of dimensionless parameters of Weibull distribution from typical wind farms |
综上对比分析可知, 各风电场实况风速威布尔概率分布的形状参数和尺度参数呈现出一定的季节相关性, 各参数的变化特征说明, 南湫风速的阵性变化6月比9月强, 黑崖子、干河口的阵性变化9月较强; BJ-RUC数值模式对风速阵性变化的预报能力存在局限性, 主要表现在预报风速的阵性变化相对较小(即预报风速相对于实况风速变化比较平缓), 预报风速偏大。
5 误差订正及效果分析针对2016年6月和9月各风电场预测风速进行滚动订正, 图 4为9月订正前后的预测风速和实况风速对比曲线。从图 4中可见, 对比预测风速序列与实况风速序列(蓝色和黑色曲线)可见, 部分时刻预测风速极大值比实况风速极大值偏大[图 4(a)~(c)中黑色矩形框]。另外, 预测风速曲线分布存在趋势滞后或呈现反位相变化趋势的现象[图 4(a)~(c)中灰色矩形框], 可见数值模式对风速的极值及趋势的描述能力也存在一定的局限性。
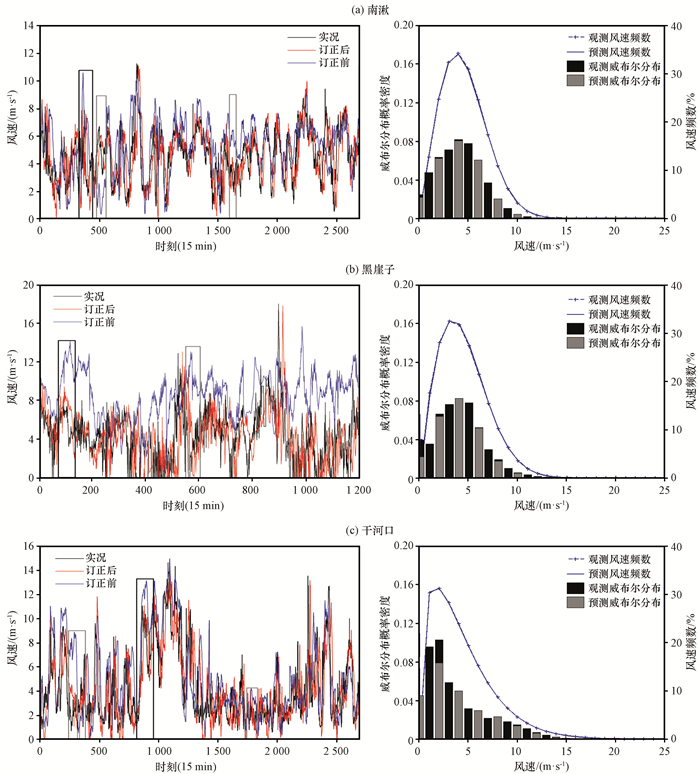
|
图 4 2016年9月南湫、黑崖子、干河口风电场实况和订正风速曲线对比(左)、威布尔分布及风频统计(右) Figure 4 The comparison (left), Weibull distributions and frequency (right) of observed wind speed and corrected wind speed of Nanqiu, Heiyazi and Ganhekou in September 2016 |
从图 4(a)预测风速曲线(蓝色)可见, 预测风速比实况相比普遍偏大。订正前南湫风电场9月的相关系数、绝对误差、均方根误差分别达51.5%、1.55 m·s-1、1.98 m·s-1(表 3中的各风电场相关系数检验P < 0.001, 均通过显著性检验), 订正后预测风速与实况风速的相关系数提升了6.8%, 达58.3%。干河口、黑崖子风电场订正后绝对误差、均方根误差也有所降低, 分别达1.30 m·s-1和1.66 m·s-1。订正前预测风速和实况风速9月平均值分别为5.30 m·s-1和4.6 m·s-1, 预报风速订正后平均值为4.59 m·s-1, 相对接近实况观测风速的平均值, 风速曲线变化趋势更加接近实况风速曲线。经过卡尔曼滤波风速订正后, 预报风速的威布尔分布形状和尺度参数修正为2.09和5.186, 可见对于南湫9月份风速样本的整体修正效果明显, 尤其是对于南湫风电场6~8 m·s-1风速段的修正效果最为显著, 使得预报风速订正前后风速频数百分比从21.89%降至12.11%, 而实际该风速段频数百分比为12.56%。
| 表 3 2016年6月和9月典型风电场风速误差评价指标统计 Table 3 Statistics of error indices of typical wind farms in June and September of 2016 |
从图 4(b)可见, 黑崖子风电场预测风速普遍偏高, 平均值达8.5 m·s-1, 预测风速与实况风速9月的相关系数23.20%, 订正后两者的相关系数提高至38.48%; 9月的平均绝对误差和均方根误差也得到显著改善, 从4.53 m·s-1和5.17 m·s-1分别降低至2.28 m·s-1和2.93 m·s-1; 订正后预测风速威布尔概率分布的形状参数和尺度参数逼近实况风速的概率分布参数[图 4(b)]。干河口风电场预测风速订正后, 9月的相关系数、平均绝对误差、均方根误差也得到了一定的改善, 分别达72.12%、1.68 m·s-1和2.22 m·s-1。订正后预测风速的威布尔分布形状参数和尺度参数由1.67和5.85修正至1.318和4.639[图 4(c)]。
统计6月和9月南湫风电场预测风速订正前后的日均方根变化(图 5)发现, 6月和9月订正后预测风速的日均方根误差分布曲线基本上都高于实况风速日均方根误差曲线, 日均方根误差[9月13日, 图 5(b)]最大改善量达2.29 m·s-1, 由6.84 m·s-1降低至4.55 m·s-1。
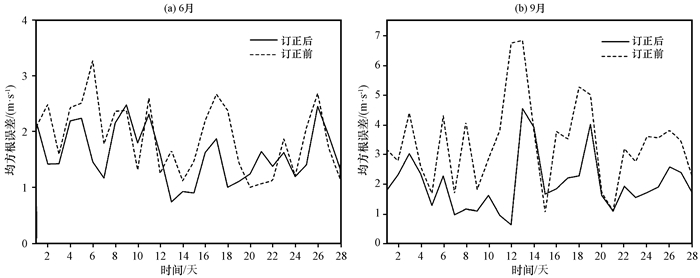
|
图 5 2016年6月和9月南湫风电场预测风速和订正后风速的日均方根误差变化 Figure 5 The root mean square variation of forecast wind speed and corrected wind speed of the wind farm in Nanqiu in June and September of 2016 |
在南湫、黑崖子、干河口风电场风速、风向分布特征分析的基础上, 基于卡尔曼滤波方法建立了风速订正模型, 对2016年6月和9月各风电场的预报风速进行误差订正及订正效果分析。得出以下结论:
(1) 南湫、黑崖子、干河口风电场的有效风速时数占全年风速时数的百分比分别达90.9%、85.06%和82.93%;各季有效风速时数存在显著的时空差异, 夏季、秋最大, 各风电场最大分别可达29.65%、27.19%和23.24%。不同的地形条件下风速分布日变化特征显明, 夏季南湫、黑崖子、干河口风速分别呈多峰多谷(或双峰双谷)、单峰单谷、双峰单谷的特征。
(2) 夏、秋季南湫风电场主导风向为东南风; 黑崖子主导风向存在明显的季节性转变, 夏季到秋季风向由偏东风转换为偏西风。干河口风向比较稳定, 主导风向持续为东风或偏东风。
(3) 南湫风电场风速的阵性变化6月比9月强, 黑崖子、干河口风电场风速的阵性变化9月较强; BJ-RUC数值模式对风速阵性变化、风速极值的预报能力存在局限性, 主要表现在预报风速的阵性变化相对较小, 预报风速偏大。
(4) 卡尔曼滤波订正模型对预报风速修正效果较为显著, 订正后预测风速的威布尔分布形状参数和尺度参数逼近实况风速的分布参数, 3家风电场风速相关系数可提高15%左右; 绝对误差、均方根误差最低可降至1.30 m·s-1和1.66 m·s-1; 订正后预报风速变化趋势滞后(或反位相变化趋势)改进明显; 对风速阵性特征描述能力增强。
致谢 感谢审稿人对本文提出的宝贵意见。感谢中国气象局和中国华电集团提供的数据支持。
Conradsen K, Nielsen L B, Prahm L P. 1984. Review of Weibull statistics for estimation of wind speed distributions[J]. J Appl Meteor, 23(23): 1173–1183.
|
|
Marzban C, Stumpf G J. 1998. A neural network for damaging wind prediction[J]. Wea Forecasting, 13(1): 151–163.
DOI:10.1175/1520-0434(1998)013<0151:ANNFDW>2.0.CO;2 |
|
Wang C H, Feng S L. 2014. Error features and their possible causes in simulated low-level winds by WRF at a wind farm[J]. Wind Energy, 17(9): 1315–1325.
|
|
曹杨, 陈洪滨, 王普才. 2017. 声雷达资料可靠性及近地面边界层风场特征分析[J]. 高原气象, 36(5): 1315–1324.
Cao Y, Chen H B, Wang P C. 2017. Analysis of the data reliability and wind field characteristics near surface boundary layer with doppler sodar observations[J]. Plateau Meteor, 36(5): 1315–1324.
DOI:10.7522/j.issn.1000-0534.2016.00100 |
|
龚伟俊, 李为相, 张广明, 等. 2011. 基于威布尔分布的风速概率分布参数估计方法[J]. 可再生能源, 29(6): 20–23.
Gong W J, Li W X, Zhang G M, et al. 2011. The estimation algorithm on the probabilistic distribution parameters of wind speed based on Weibull distribution[J]. Renew Energy Res, 29(6): 20–23.
DOI:10.3969/j.issn.1671-5292.2011.06.005 |
|
黄凤新, 2013.基于卡尔曼滤波的复杂地形WRF模式预报风速订正[D].南京: 南京信息工程大学, 1-68.
Huang F X, 2013. The WRF model forecast wind speed correction under complex terrain based on Kalman Filter[D]. Nanjing: University of Information Science and Technology, 1-68.
http://cdmd.cnki.com.cn/Article/CDMD-10300-1013340892.htm |
|
姜广绪, 潘晶雯, 田景奎, 等. 2015. 双参数威布尔分布风况中基于k值分析的能量分布研究[J]. 电力建设, 36(3): 105–108.
Jiang G X, Pan J W, Tian J K, et al. 2015. Energy distribution research based on the parameter K analysis of two-parameter Weibull distribution wind conditions[J]. Electric Power Construction, 36(3): 105–108.
DOI:10.3969/j.issn.1000-7229.2015.03.018 |
|
孔玉寿, 钱建明, 臧增亮, 等. 2010. 统计天气预报原理与方法[M]. 北京: 气象出版社, 441-447.
Kong Y S, Qian J M, Zang Z L, et al. 2010. Statistical weather prediction principles and methods[M]. Beijing: China Meteorological Press, 441-447.
|
|
李晓霞, 黄涛, 王兴, 等. 2017. 兰州新区近地层风场时空特征分析[J]. 高原气象, 36(4): 1001–1009.
Li X X, Huang T, Wang X, et al. 2017. Analysis of characters of wind field in surface layer in Lanzhou New District[J]. Plateau Meteor, 36(4): 1001–1009.
DOI:10.7522/j.issn.1000-0534.2016.00092 |
|
陆如华, 徐传玉, 张玲, 等. 1997. 卡尔曼滤波的初值计算方法及其应用[J]. 应用气象学报, 14(1): 34–43.
Lu R H, Xu C Y, Zhang L, et al. 1997. Calculation method for initial value of Kalman Filter and its application[J]. J Appl Meteor, 14(1): 34–43.
|
|
沈德昌. 2015. 我国大型风电机组技术发展情况[J]. 太阳能(2): 11–14.
Sheng D C. 2015. The development of large-scale wind turbines in China[J]. Solar Energy(2): 11–14.
DOI:10.3969/j.issn.1003-0417.2015.02.003 |
|
石岚, 徐丽娜, 郝玉珠. 2017. 多模式风速融合预报应用研究[J]. 高原气象, 36(4): 1022–1028.
Shi L, Xu L N, Hao Y Z. 2017. Application research on the multi-model fusion forecast of wind speed[J]. Plateau Meteor, 36(4): 1022–1028.
DOI:10.7522/j.issn.1000-0534.2017.00021 |
|
孙丹, 2015.风力发电系统对电网暂态稳定性影响的分析与研究[D].北京: 华北电力大学, 1-51.
Sun D, 2015. Analysis and research on transient stability of power system integrated with wind power generation[D]. Beijing: North China Electric Power University, 1-51.
|
|
孙学金, 李岩, 张燕鸿, 等. 2017. 基于WRF-LES的干旱湖区近地面风场模拟与敏感性研究[J]. 高原气象, 36(3): 835–844.
Sun X J, Li Y, Zhang Y H, et al. 2017. Near-Surface wind simulation over acrid lakeshore area and sensitivity studies using the WRF-LES[J]. Plateau Meteor, 36(3): 835–844.
DOI:10.7522/j.issn.1000-0534.2016.00058 |
|
严彦, 许昌, 刘德有, 等. 2011. 测风数据的时间间隔对风速概率分布参数计算的影响[J]. 可再生能源, 29(6): 24–28.
Yan Y, Xu C, Liu D Y, et al. 2011. Study on probabilistic distribution parameters of wind speed influenced by different anemometer time intervals[J]. Renew Energy Res, 29(6): 24–28.
DOI:10.3969/j.issn.1671-5292.2011.06.006 |
|
余江, 江志红, 俞卫, 等. 2015. 风电场风速数值预报的误差分析及订正[J]. 气象科学, 35(5): 587–592.
Yu J, Jiang Z H, Yu W, et al. 2015. Error analysis and correction of wind speed numerical forecast at wind farm[J]. J Meteor Sci, 35(5): 587–592.
|
|
张飞民, 王澄海. 2014. 利用WRF-3DVAR同化常规观测资料对近地层风速预报改进的试验[J]. 高原气象, 33(3): 675–685.
Zhang F M, Wang C H. 2014. Experiment of surface-layer wind forecast improvement by assimilating conventional data with WRF-3DVAR[J]. Plateau Meteor, 33(3): 675–685.
DOI:10.7522/j.issn.1000-0534.2012.00198 |
|
张兰慧, 尚可政, 程一帆, 等. 2011. 数值预报产品的误差订正方法[J]. 兰州大学学报(自然科学版), 47(3): 44–49.
Zhang L H, Shang K Z, Cheng Y F, et al. 2011. Study on the correction of numerical prediction products[J]. Journal of Lanzhou University (Natural Sciences), 47(3): 44–49.
|
|
张双益, 胡非. 2017. 大气边界层与风力发电的相互作用研究综述[J]. 高原气象, 36(4): 1127–1137.
Zhang S Y, Hu F. 2017. Review on study of atmospheric boundary layer and wind power generation interaction[J]. Plateau Meteor, 36(4): 1127–1137.
DOI:10.7522/j.issn.1000-0534.2016.00095 |
|
祝赢, 柳艳香, 程兴宏, 等. 2013. 线性滚动极值处理方法对数值模拟风速的订正研究[J]. 热带气象学报, 29(4): 681–686.
Zhu Y, Liu Y X, Cheng X H, et al. 2013. A research on revision of simulated wind speed based on linear rolling and extremum procession[J]. J Trop Meteor, 29(4): 681–686.
DOI:10.3969/j.issn.1004-4965.2013.04.018 |
 2018, Vol. 37
2018, Vol. 37