2. 中国科学院青藏高原研究所, 北京 100101;
3. 中国科学院大学, 北京 100101;
4. 中国科学院青藏高原环境变化与地表过程重点实验室, 北京 100101;
5. 中国科学院青藏高原地球科学卓越创新中心, 北京 100101;
6. 中国气象局广州热带海洋气象研究所, 广东 广州 510080
地气界面间时刻进行着物质与能量的交换, 地表通过这种交换影响着不同时空尺度的天气、气候和环境变化。地气相互作用不仅是大气科学研究的热点问题, 同时也是生态学、水文学、环境科学、地理学等学科共同关注的前沿领域(叶笃正等, 1994)。地气相互作用对气候的影响是通过感热通量、潜热通量、动量通量等影响大气环流来实现的(Seneviratne et al, 2008; 房云龙等, 2010; 解晋等, 2018)。如何精确计算地表通量一直是大气科学主要研究内容和难点问题之一(丁一汇, 1997)。
青藏高原(简称高原)素称地球的“第三极”, 其平均海拔达4 000 m以上, 它的高海拔和大地形造成的热力、动力作用对大气环流、亚洲季风以及全球气候变化均有重要影响(叶笃正, 1979; 马耀明等, 2000, 2006; 杨健等, 2012; 周亚等, 2017; 张长灿等, 2017)。高原五大圈层(大气圈、水圈、岩石圈、生物圈和冰冻圈)的多圈层相互作用既是引起所有变化的驱动器(马耀明, 2012), 也是对全球气候变化响应最为敏感的地区之一(Liu et al, 2000)。高原对大气的热力及动力作用主要是通过地气相互作用, 以湍流方式进行物质与能量交换而实现的(冯璐等, 2016), 因此估算高原地区地表能量通量, 深入理解高原地区地气相互作用的特征和规律变得尤为重要。
传统的地表能量通量测量技术基于站点观测来实现, 而对于下垫面类型和地形均复杂多变的高原来说, 这种站点观测难以满足更大空间尺度的研究需求(Ma et al, 2002a, 2002b)。卫星遥感可以方便快速的获取区域乃至全球地表特征参数, 弥补了站点观测空间代表性不足, 成为获取区域地表能量通量的重要手段(田辉等, 2009; 黄春林等, 2014)。目前国内外利用遥感数据估算地表通量使用较多的模型有地表能量平衡算法S-SEBI(Simplified Surface Energy Balance Index)(Roerink et al, 2000)、地表能量平衡系统SEBS(Surface Energy Balance System)(Jia et al, 2003; Su et al, 2002, 2005)、陆地地表能量平衡算法SEBAL(Surface Energy Balance Algorithm for Land)(Bastiaanssen et al, 1998a, 1998b)、自校准的蒸散制图模型METRIC(Mapping Evapotranspiration at high Resolution with Internalized Calibration)(Allen et al, 2007)、双源模型TSM(Two-Source Model)(Norman et al, 1995)和双源能量平衡模型TSEB(Two-Source Energy Balance)(Sánchez et al, 2008)等。SEBS模型(Su, 2002)是在蒸发比的概念基础上, 基于Monin-Obukhov相似理论, 利用卫星遥感数据和近地层实测气象数据估算地表能量通量的单源地表能量平衡模型。SEBS模型考虑了极干、极湿这两种极端情况, 能很好的反映出研究区域能量和水分空间分布的差异性, 使得地表能量通量估算的精度得到了提高(王国华等, 2011); 且该模型几乎完全基于物理过程, 不需要任何先验知识, 因此在国内外得到广泛应用(Chen et al, 2013; Huang et al, 2015; Shoko et al, 2015; 金学杰等, 2017)。
但在以往地表能量通量的估算研究中, 通常直接用站点实测资料验证模型估算精度, 没有对地表通量观测数据中存在的能量不平衡问题给予足够重视, 验证结果存在相当大的不确定性。以往诸多研究均表明在地表通量观测中广泛存在的“能量不闭合”问题(Twine et al, 2000; Lee et al, 2002; Mauder et al, 2007; Yang et al, 2008), 而造成这种问题的主要原因是通量观测中的采样误差、测量仪器的系统误差、其他能量源汇项的忽略、高低频湍流通量的损失及受平流的影响。利用涡动相关法的测量可以计算得到站点湍流热通量(感热通量、潜热通量), 计算过程中需要进行一些必要的修正(王介民等, 2007), 尽管如此, 在大气状态平稳、均一的下垫面条件下, 涡动相关法仍然存在对湍流热通量低估的问题, 是造成“能量不闭合”问题的根本所在(王介民等, 2009)。Pan et al(2017)指出利用涡动相关法会明显低估潜热通量, 而基于地表能量平衡方程与近地层梯度扩散理论的波文比校正法可以有效的改善涡动相关法对潜热通量的低估问题。本文基于高原地区3个站点的地表通量观测数据, 探究实测数据中反映出的能量不平衡现象, 通过波文比校正法校正潜热通量来改善站点实测数据中“能量不闭合”的问题, 并利用站点实测数据检验评估SEBS模型对不同下垫面地气能量交换的估算能力。
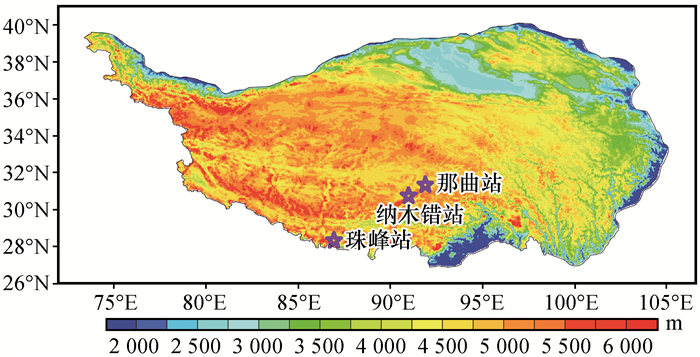
2 数据选取与方法介绍 2.1 数据选取所用数据主要为近地层气象观测资料和卫星遥感数据。近地层气象观测资料包括辐射资料、地表能量通量资料和大气边界层塔站观测资料, 包括太阳短波辐射、大气长波逆辐射、湍流通量、土壤热通量(5 cm)、气压、气温、相对湿度、风速, 时间分辨为30 min。基于台站架设的开路涡动协方差测量系统直接观测的三维风速、超声虚温、水汽等变量, 选用德国Bayreuth大学开发的TK3数据处理软件包计算得到感热通量和潜热通量。TK3基于涡动相关法计算取样时长为30 min的湍流通量, 并对通量结果进行质量控制和质量状况评估。在使用TK3计算感热、潜热数据时, 对湍流原始数据进行了野点去除、坐标旋转、频率损失订正、超生虚温订正、WPL修正的处理。根据TK3对湍流通量的质量状况的划分(Foken et al, 1996), 结合简化的三类质量判别标准(Foken et al, 2004; 王介民, 2012), 选用数据质量状况QA<4的感热、潜热数据用于本文研究。为了更好的探究高原地区不同下垫面条件下地表能量通量的模型估算效果, 选取那曲站、纳木错站和珠峰站2008年的数据。3个站点的空间位置如图 1和表 1所示。
|
图 1 高原观测站点的位置 Fig. 1 Location of observation stations over the Qinghai-Tibetan Plateau |
| 表 1 观测站点简介 Table 1 Introduction of the observation stations |
卫星遥感数据选用搭载在Terra卫星上的中分辨率成像光谱辐射仪MODIS数据。MODIS地表反射率逐日产品的空间分辨率为500 m。为了保证研究数据的一致性, 对地表反射率产品进行投影转化和重采样, 并根据站点坐标提取出对应的像元值。
2.2 方法 2.2.1 土壤温度预报校正TDEC法由于那曲站土壤热通量板的观测数据位于10 cm、20 cm深度, 缺少地表土壤热通量数据, 而且土壤热通量板的热传导系数往往和实际土壤并不一致。因此利用实测土壤温湿度资料, 结合土壤温度预报校正TDEC法(阳坤等, 2008; 冯璐等, 2016)估算地表土壤热通量。土壤一维热传导方程为(葛骏等, 2016):
| $ \frac{{\partial T}}{{\partial t}} = - \frac{1}{{{\rho _s}{c_s}}}\frac{{\partial G}}{{\partial z}}, $ | (1) |
式中: T为土壤温度(单位: K); t为时间(单位: s); ρscs为土壤的体积热容量(单位: J·kg-1·K-1); G为土壤热通量(单位: W·m-2); z为土壤深度(单位: cm)。积分方程(1)得到:
| $ G\left( z \right) = G\left( {{z_{{\rm{ref}}}}} \right) + \int\limits_{{z_{{\rm{ref}}}}}^z {\frac{{\partial {\rho _s}{c_s}T\left( z \right)}}{{\partial t}}{\rm{d}}z} , $ | (2) |
式中: G(zref)为某一参考层zref处的土壤热通量。若已知温度廓线为T(zi), 则方程(2)的离散形式为:
| $ \begin{array}{*{20}{c}} {G\left( {z,t} \right) = G\left( {{z_{{\rm{ref}}}},t} \right) + \frac{1}{{\Delta t}}\sum\limits_{{z_{{\rm{ref}}}}}^z {\left[ {{\rho _s}{c_s}\left( {{z_i},t + \Delta t} \right)T\left( {{z_i},t} \right.} \right.} }\\ {\left. {\left. { + t} \right) - {\rho _s}{c_s}\left( {{z_i},t} \right)T\left( {{z_i},t} \right)} \right]\Delta z.} \end{array} $ | (3) |
若假设土壤热传导系数为一常数(如1.0 W·m-1·K-1), 通过土壤热扩散方程得到土壤温度的基本廓线TTDEC, 并用实测土壤温度廓线来修正TTDEC, 最后利用公式(3)可以计算出各层的土壤热通量。
2.2.2 NDVI的去云处理和地表比辐射率估算方法SEBS模型的输入数据中包括归一化差值植被指数NDVI和地表反射率。由于MODIS NDVI产品时间分辨率较低(16天或月), 因此利用MODIS逐日地表反射率产品计算NDVI:
| $ NDVI = \frac{{{\rho _2} - {\rho _1}}}{{{\rho _2} + {\rho _1}}}, $ | (4) |
式中: ρ1为可见光波段反射率; ρ2为近红外波段反射率。由于卫星传感器对地面进行观测时, 会受到观测角度、太阳高度角及云覆盖状况的影响, 使卫星遥感观测值包含大量噪音。这些噪音的存在使得到的NDVI随时间的变化呈现无规律的状态, 难以进行应用。选用时间序列谐波分析HANTS算法对NDVI进行去云处理, 滤去噪音影响, 重建高质量的NDVI数据。
HANTS算法是以傅立叶变换为基础的谐波分析法(Zhong et al, 2010), 该方法首先是将所有时间序列像元点进行傅里叶变换, 然后选择几个低频分量进行反傅里叶变换, 得到新的时间序列; 通过比较观测值与拟合值, 将明显偏离拟合曲线的点视为云污染点, 用新曲线对应的值进行替换; 对改变后的原始序列重复上述过程, 通过这种反复迭代过程重建NDVI时间序列。
在重建NDVI数据基础上, 利用NDVI阈值法(Sobrino et al, 2003)对植被和裸土进行地表比辐射率的估算。其计算方法如下:
| $ \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} \varepsilon = 0.958,\\ \varepsilon = 0.971 + 0.018{f_c},\\ \varepsilon = 0.980 - 0.042{\rho _1}, \end{array}&\begin{array}{l} NDVI > 0.5\\ 0.2 \le NDVI \le 0.5\\ NDVI < 0.2 \end{array} \end{array}} \right. $ | (5) |
式中: ε为地表比辐射率; fc=
在忽略能量的水平输送并假定植被光合作用及生物累积消耗能量的情况下, 地表能量平衡方程可写为:
| $ {R_n} = {G_0} + H + LE, $ | (6) |
式中: Rn为地表净辐射通量(单位: W·m-2); G0为0 cm处的土壤热通量(单位: W·m-2)(简称为土壤热通量); H为感热通量(单位: W·m-2); LE为潜热通量(单位: W·m-2)。
地表净辐射通量Rn是地表和大气之间能量和物质相互交换的主要能量来源。它主要是由太阳辐射、地表反射辐射、大气逆辐射和地表发射辐射四部分构成, 因此地表净辐射通量的计算公式可表示为:
| $ {R_n} = {R_{{\rm{swd}}}} - \alpha {R_{{\rm{swd}}}} + \varepsilon {R_{{\rm{lwd}}}} - \varepsilon \sigma {T_0}^4, $ | (7) |
式中: Rswd为太阳辐射(单位: W·m-2); Rlwd为大气逆辐射(单位: W·m-2); α为地表反照率; ε为地表比辐射率; σ=5.76×10-8 W·m-2·K-4, 为Stefan-Boltzman常数; T0为地表温度(单位: K)。
土壤热通量的大小主要与地表净辐射及地表覆盖状况有关, Su(2002)提出用裸土和植被下垫面覆盖比例与净辐射通量乘积的叠加来计算土壤热通量, 其计算公式为:
| $ {G_0} = {R_n}\left[ {{\mathit{\Gamma }_c} + \left( {1 - {f_c}} \right)\left( {{\mathit{\Gamma }_s} - {\mathit{\Gamma }_c}} \right)} \right], $ | (8) |
式中: Γs=0.05和Γc=0.315分别为完全裸土和完全植被条件下土壤热通量与地表净辐射通量的比率。感热通量的计算则是基于Monin-Obukhov相似理论, 可以通过迭代以下三个方程得到:
| $ {U_z} = \frac{{{u_ * }}}{k}\left[ {\ln \left( {\frac{{z - {d_0}}}{{{z_{0m}}}}} \right) - {\mathit{\Psi }_m}\left( {\frac{{z - {d_0}}}{L}} \right) + {\mathit{\Psi }_m}\left( {\frac{{{z_{0m}}}}{L}} \right)} \right], $ | (9) |
| $ {\theta _0} - {\theta _a} = \frac{H}{{k{u_ * }\rho {C_p}}}\left[ {\ln \left( {\frac{{z - {d_0}}}{{{z_{0h}}}}} \right) - {\mathit{\Psi }_h}\left( {\frac{{z - {d_0}}}{L}} \right) + {\mathit{\Psi }_h}\left( {\frac{{{z_{0h}}}}{L}} \right)} \right] $ | (10) |
| $ L = - \frac{{\rho {C_\rho }u_ * ^3{\theta _v}}}{{kgH}}, $ | (11) |
式中: z为观测高度(单位: m); z0m为空气动力学粗糙度长度(单位: m); d0为零平面位移高度(单位: m); Uz为高度z处的风速(单位: m·s-1); u*为摩擦速度(单位: m·s-1); k=0.4为von Kármán常数; Ψm为动量稳定度订正函数; θ0为表面位温(单位: K); θa为高度z处的大气位温(单位: K); z0h为热力学粗糙长度(单位: m); ρ为大气密度(单位: kg·m-3); Cp为空气比热(单位: J·kg-1·K-1); Ψh为感热稳定度订正函数; L为Monin-Obukhov长度; g为重力加速度(单位: m·s-2); θv为表面虚位温(单位: K)。
SEBS模型求解潜热通量的过程中, 通过地表干湿状态对地表潜热通量的结果进行限定。在土壤水分亏缺的条件下, 由于水分的限制, 潜热通量约为0 W·m-2, 此时感热通量取到最大值:
| $ {H_{{\rm{dry}}}} = {R_n} - {G_0}, $ | (12) |
其中: Hdry为干燥地表条件下的感热通量。而在土壤水分充足的条件下, 蒸发达到最大, 此时感热通量达到最小值:
| $ {H_{{\rm{wet}}}} = {R_n} - {G_0} - L{E_{{\rm{wet}}}}, $ | (13) |
式中: Hwet为湿润地表条件下的感热通量; λEwet为湿润条件下的潜热通量。SEBS模型中将蒸散发速率与潜在蒸散发的比值定义为相对蒸发比Λr:
| $ {\mathit{\Lambda }_r} = \frac{{LE}}{{L{E_{{\rm{wet}}}}}} = 1 - \frac{{H - {H_{{\rm{wet}}}}}}{{{H_{{\rm{dry}}}} - {H_{{\rm{wet}}}}}}, $ | (14) |
实际蒸发比Λ定义为实际蒸散发与可用通量的比值:
| $ \mathit{\Lambda } = \frac{{LE}}{{{R_n} - {G_0}}} = \frac{{{\mathit{\Lambda }_r}L{E_{{\rm{wet}}}}}}{{{R_n} - {G_0}}}, $ | (15) |
最后, 基于公式(11)~(14)可计算得到潜热通量。
2.2.4 波文比校正法波文比校正法的理论基础是地表能量平衡方程与近地层梯度扩散理论, 结合净辐射通量和土壤热通量数据, 可以校正站点实测潜热通量(Twine et al, 2000; Wilson et al, 2002)。波文比校正法计算公式如下:
| $ BRLE = \frac{1}{{1 + \beta }}\left( {{R_n} - {G_0}} \right), $ | (16) |
式中: BRLE为校正后的潜热通量; 波文比β=
为了评估模型的估算结果, 选择以下统计指标:均方根误差RMSE、平均偏差MB和相关系数R。计算公式如下:
| $ RMSE = \sqrt {\frac{{\sum\limits_{i = 1}^N {{{\left( {{x_i} - ob{s_i}} \right)}^2}} }}{N}} , $ | (17) |
| $ MB = \frac{{\sum\limits_{i = 1}^N {\left( {{x_i} - ob{s_i}} \right)} }}{N}, $ | (18) |
| $ R = \frac{{\sum\limits_{i = 1}^N {\left( {{x_i} - \bar x} \right)\left( {ob{s_i} - \overline {obs} } \right)} }}{{\sqrt {\sum\limits_{i = 1}^N {{{\left( {{x_i} - \bar x} \right)}^2}} } \sqrt {\sum\limits_{i = 1}^N {{{\left( {ob{s_i} - \overline {obs} } \right)}^2}} } }}, $ | (19) |
式中: xi和obsi分别为估算值和观测值; x和obs分别为估算值的均值和观测值的均值; N为样本个数。
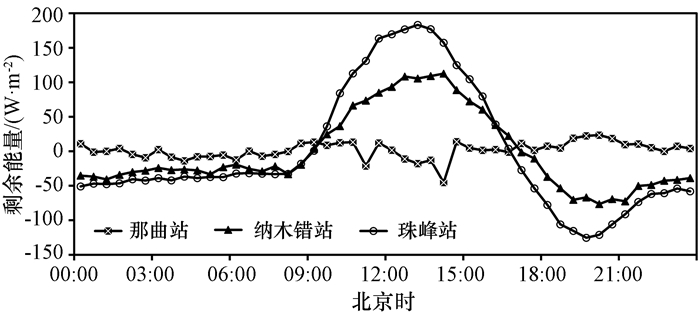
3 结果分析 3.1 地表能量闭合率特征如果忽略冠层的热存储项和水平热平流项, 从地表能量平衡方程[式(6)]可知理论上净辐射应该等于感热通量、潜热通量和土壤热通量之和。但实际观测表明, 多数情况下会有剩余能量的存在(Oncley et al, 2007; Foken, 2008; Zuo et al, 2012)。剩余能量为净辐射通量与感热通量、潜热通量和土壤热通量的差值, 即Rn-(G0+H+LE)。图 2为3个站点剩余能量的日变化。从图 2中可以看出, 那曲站的剩余能量日变化比较平缓, 而其余2个站点的剩余能量具有明显的日变化特征, 剩余能量日变化趋势呈明显的“S”形分布, 日出前变化趋势比较平缓, 日出后随着太阳高度角的增大而增大, 在14:00(北京时, 下同)左右达到最大值后, 随后随着太阳高度角的减小而减小, 19:00达到最小值, 随后呈上升趋势最后逐渐趋于平缓。那曲站、纳木错站和珠峰站剩余能量的标准差分别为12.29, 55.65和88.90 W·m-2, 日变化绝对值的均值分别为9.36, 47.86和74.22 W·m-2。相比纳木错站和珠峰站, 那曲站日变化幅度最小。需要指出的是那曲站是根据实测土壤温湿度计算得到的土壤热通量, 较接近真实值, 另外两个站点是热通量板测量数据(由于纳木错站和珠峰站的土壤温湿度数据缺测值较多, 无法使用TDEC法估算土壤热通量, 故只能使用热通量板测量数据)。造成这种差异的原因可能是土壤热通量板低估了土壤热通量(冯璐等, 2016), 客观上导致剩余能量偏大。上述结果一方面表明站点观测数据存在能量不平衡现象, 另一方面说明站点观测数据存在能量不平衡现象的部分原因是由于土壤热通量板低估地表土壤热通量造成的。
|
图 2 各站点剩余能量的日变化 Fig. 2 Diurnal variation of residual energy at different stations |
为了进一步探究造成站点实测数据能量不平衡现象的其他原因, 根据地表能量平衡方程, 采用两种不同方法计算蒸发比1(ef1)和蒸发比2(ef2):
| $ ef1 = \frac{{LE}}{{{R_n} - {G_0}}}, $ | (20) |
| $ ef2 = \frac{{LE}}{{LE + H}}. $ | (21) |
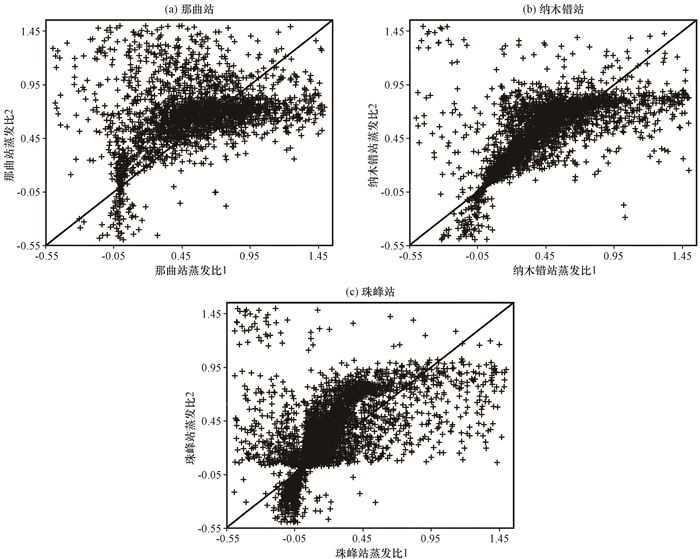
图 3(a)~(c)分别为那曲站、纳木错站和珠峰站的ef1和ef2对比图, 从图 3中可以明显看出高于1:1线的数据较多。分别对那曲站、纳木错站和珠峰站的ef2/ef1比值进行统计, 结果表明分别有63.47%, 70.41%和68.41%的比值大于1, 3个站点的蒸发比ef1明显小于蒸发比ef2, 这是由于站点实测的净辐射通量与土壤热通量的差值大于潜热通量与感热通量之和。
|
图 3 各站点蒸发比1与蒸发比2对比 Fig. 3 Comparsion betweenevaporation fraction 1 and evaporation fraction 2 at different stations |
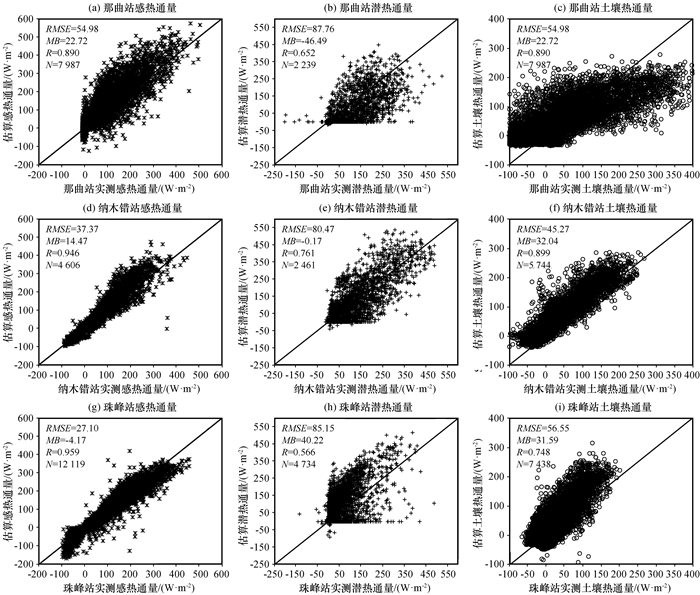
通过SEBS模型中计算方法即公式(7)~(11)可以估算得到地表通量, 利用站点实测数据对模型估算结果进行验证, 并计算均方根误差、平均偏差和相关系数。图 4为SEBS模型估算的地表通量与站点实测值的对比。从图 4中可以明显的看出, SEBS模型估算的感热通量、土壤热通量与站点实测数据两者具有较好的一致性, 而估算的潜热通量与实测值一致性较差。那曲站、纳木错站和珠峰站感热通量的均方根误差分别为54.98, 37.37和27.10 W·m-2, 平均偏差分别为22.72, 14.47和-4.17 W·m-2, 相关系数分别为0.890, 0.946, 0.959;土壤热通量的均方根误差分别为57.09, 45.27和56.55 W·m-2, 平均偏差分别为12.28, 32.04和31.59 W·m-2, 相关系数分别为0.805, 0.899, 0.748;潜热通量的均方根误差分别为87.76, 80.47和85.15 W·m-2, 平均偏差分别为-46.49, -0.17和40.22 W·m-2, 相关系数分别为0.652, 0.761和0.566。统计指标表明, SEBS模型估算感热通量的效果较好, 估算土壤热通量的效果次之, 而估算潜热通量的效果最差。土壤热通量的估算偏差是由于公式(8)计算土壤热通量方法是在均质土壤条件推导出来的, 且忽略了地表温度因素的影响(Su et al, 2006)。而模型估算的潜热通量验证结果偏差较大和站点实测数据存在“能量不闭合”问题相关。
|
图 4 SEBS模型估算的地表能量通量的验证 Fig. 4 Validation of surface energy fluxes estimated by SEBS model with in-situ measurements |
站点地表通量观测数据中存在能量不平衡现象, 且实际观测的潜热通量数据偏小(Twine et al, 2000; Wilson et al, 2002; Wolf et al, 2008; Majozi et al, 2017; Pan et al, 2017)。而以地表能量平衡为基础的波文比校正方法可以较好的改善这种问题(Twine et al, 2000; Wilson et al, 2002; Pan et al, 2017)。为了定量评估该校正法, 分别对3个站点的地表可利用能量(净辐射通量与土壤热通量之差, 即: Rn-G0)和湍流通量之和(感热通量和潜热通量之和, 即: H+LE)进行线性回归分析。图 5为那曲站、纳木错站和珠峰站的潜热通量校正前后的能量闭合的对比。从图 5中可以看出, 那曲站校正前线性系数回归系数分别为截距为44.887, R2为0.59, 斜率为0.664, 即地表能量闭合率为66.4%;校正后的线性回归系数为截距为21.451, R2为0.92, 斜率为0.858, 即地表能量闭合率为85.8%。那曲站、纳木错站和珠峰站3个站校正前后相比, 截距分别减少了23.436, 36.836和28.723; R2分别提高了0.33, 0.25和0.27;能量闭合率分别提高了19.4%, 21.4%和19.1%。根据对3个站点的Rn-G0和H+LE进行线性回归分析的结果可知, 波文比校正方法可以较好的改善站点地表通量观测数据能量不平衡的现象。
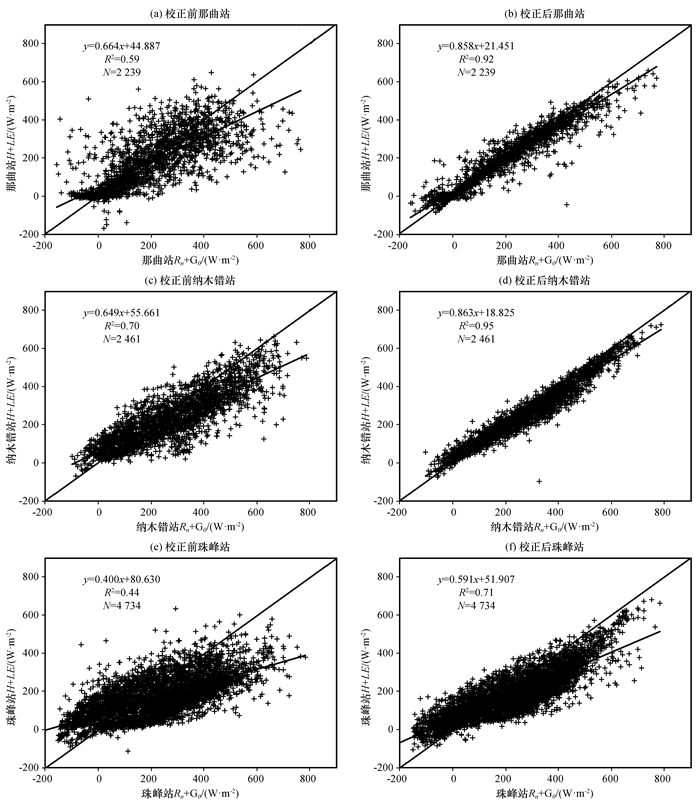
|
图 5 潜热通量校正前后能量闭合对比 Fig. 5 Comparison between energy closure before and after correction of latent heat flux |
在地表能量闭合率校正之后, 进一步利用校正后的潜热通量对模型估算结果进行评估。图 6为那曲站、纳木错站和珠峰站的模型估算的潜热通量与校正后站点实测值的对比图, 其中3个站点潜热通量校正后均方根误差分别80.98, 46.99和55.84 W·m-2; 平均误差为-34.79, -21.63和26.17 W·m-2; 相关系数分别为0.804, 0.946和0.846。结果表明, 相比于站点实测校正前, SEBS模型估算结果与校正后的潜热通量有较好的一致性。
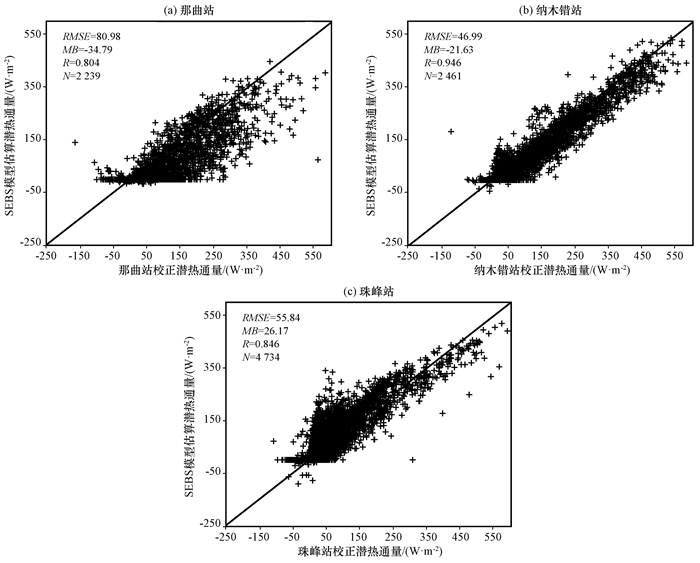
|
图 6 SEBS模型估算的潜热通量与站点实测值校正后的对比 Fig. 6 Comparison between the latent heat flux estimated by the SEBS model and the corrected in-situ measurements |
使用MODIS卫星资料计算出地表参数(NDVI、地表比辐射率)结合站点实测资料, 利用SEBS模型估算了青藏高原地区3个站点2008年全年的地表能量通量, 并利用站点实测资料评估模型估算结果, 探究和改善地表能量通量观测数据中存在的“能量不闭合”问题, 所得主要结论如下:
(1) 那曲站、纳木错站和珠峰站地表通量观测数据存在能量不平衡的现象, 3站能量闭合率分别为66.4%, 64.9%和40.0%。剩余能量的日变化呈“S”型分布, 日出前变化趋势比较平缓, 日出后随着太阳高度角的增大而增大, 在午后达到最大值, 随后随着太阳高度角的减小而减小, 达到最小值后, 随后上升, 最后逐渐趋于平缓。
(2) SEBS模型估算的感热通量和土壤热通量与站点实测数据具有较好的一致性, 而模型估算潜热通量与站点实测值一致性较差; 统计指标表明, 模型估算的感热通量和土壤热通量的结果优于潜热通量。
(3) 基于波文比校正方法对潜热通量观测数据进行校正, 结果表明校正后地表能量不平衡得到明显改善:校正后3个站点的能量闭合率分别提高了19.4%%,21.4%和19.1%。
(4) 利用校正后的站点实测的潜热通量对SEBS模型估算的潜热通量进行了验证, 结果表明, SEBS模型估算结果和校正后的站点实测潜热通量具有良好的一致性。因此在利用实测站点数据对各种卫星遥感参数化模型结果进行对比验证前, 站点尺度的“能量不闭合”问题必须加以考虑。
致谢: 中国科学院那曲高寒气候环境观测研究站、中国科学院珠穆朗玛大气与环境综合观测研究站和中国科学院纳木错多圈层综合观测研究站为本研究提供了实测数据支持, 特此感谢!
Allen R G, Tasumi M, Morse A, et al. 2007. Satellite-based energy balance for mapping evapotranspiration with internalized calibration (METRIC)-Applications[J]. J Irrig Drain Eng, 133(4): 395–406.
DOI:10.1061/(ASCE)0733-9437(2007)133:4(395) |
|
Bastiaanssen W G, Menenti M, Feddes R, et al. 1998a. A remote sensing surface energy balance algorithm for land (SEBAL). 1. Formulation[J]. J Hydrol, 212: 198–212.
|
|
Bastiaanssen W G, Pelgrum H, Wang J, et al. 1998b. A remote sensing surface energy balance algorithm for land (SEBAL):Part 2:Validation[J]. J Hydrol, 212: 213–229.
|
|
Chen X, Su Z, Ma Y, et al. 2013. Estimation of surface energy fluxes under complex terrain of Mt. Qomolangma over the Tibetan Plateau[J]. Hydrol Earth Syst Sci, 17(4): 1607–1618.
DOI:10.5194/hess-17-1607-2013 |
|
Foken T, Wichura B. 1996. Tools for quality assessment of surface-based flux measurements[J]. Agri For Meteor, 78(1-2): 83–105.
DOI:10.1016/0168-1923(95)02248-1 |
|
Foken T, Göockede M, Mauder M, et al, 2004. Post-field data quality control[C]//Handbook of micrometeorology. Bostons: Kluwer Academic: 181-208.
https://link.springer.com/chapter/10.1007%2F1-4020-2265-4_9 |
|
Foken T. 2008. The energy balance closure problem:An overview[J]. Ecol Appl, 18(6): 1351–1367.
DOI:10.1890/06-0922.1 |
|
Huang C, Li Y, Gu J, et al. 2015. Improving estimation of evapotranspiration under water-limited conditions based on sebs and MODIS data in arid regions[J]. Remote Sens, 7(12): 16795–16814.
DOI:10.3390/rs71215854 |
|
Jia L, Su Z, van den Hurk B, et al. 2003. Estimation of sensible heat flux using the Surface Energy Balance System (SEBS) and ATSR measurements[J]. Phys Chem Earth, Parts A/B/C, 28(1): 75–88.
|
|
Lee X, Hu X. 2002. Forest-air fluxes of carbon, water and energy over non-flat terrain[J]. Bound-Layer Meteor, 103(2): 277–301.
DOI:10.1023/A:1014508928693 |
|
Liu X, Chen B. 2000. Climatic warming in the Tibetan Plateau during recent decades[J]. Int J Climatol, 20(14): 1729–1742.
DOI:10.1002/(ISSN)1097-0088 |
|
Ma Y, Su Z, Li Z, et al. 2002a. Determination of regional net radiation and soil heat flux over a heterogeneouslandscape of the Tibetan Plateau[J]. Hydrol Proc, 16(15): 2963–2971.
|
|
Ma Y, Tsukamoto O, Ishikawa H. 2002b. Remote sensing parameterization of the processes of energy and water cycle over desertification areas[J]. Sci China, Ser D Earth Sci, 45: 47–53.
|
|
Majozi N P, Mannaerts C M, Ramoelo A, et al. 2017. Analysing surface energy balance closure and partitioning over a semi-arid savanna FLUXNET site in Skukuza, Kruger National Park, South Africa[J]. Hydrol Earth Syst Sci, 21(7): 3401.
DOI:10.5194/hess-21-3401-2017 |
|
Mauder M, Oncley S P, Vogt R, et al. 2007. The energy balance experiment EBEX-2000. Part Ⅱ:Intercomparison of eddy-covariance sensors and post-field data processing methods[J]. Bound-Layer Meteor, 123(1): 29–54.
DOI:10.1007/s10546-006-9139-4 |
|
Norman J, Kustas W, Humes K. 1995. Source approach for estimating soil and vegetation energy fluxes in observations of directional radiometric surface temperature[J]. Agr Forest Meteor, 77: 263–293.
DOI:10.1016/0168-1923(95)02265-Y |
|
Oncley S P, Foken T, Vogt R, et al. 2007. The energy balance experiment EBEX-2000. Part Ⅰ:overview and energy balance[J]. Bound-Layer Meteor, 123(1): 1–28.
DOI:10.1007/s10546-007-9161-1 |
|
Pan X, Liu Y, Fan X, et al. 2017. Two energy balance closure approaches:applications and comparisons over an oasis-desert ecotone[J]. J Arid Land, 9(1): 51–64.
DOI:10.1007/s40333-016-0063-2 |
|
Roerink G, Su Z, Menenti M. 2000. S-SEBI:A simple remote sensing algorithm to qestimate the surface energy balance[J]. Phys Chem Earth, Part B, 25(2): 147–157.
DOI:10.1016/S1464-1909(99)00128-8 |
|
Sánchez J, Scavone G, Caselles V, et al. 2008. Monitoring daily evapotranspiration at a regional scale from Landsat-TM and ETM+ data:Application to the Basilicata region[J]. J Hydrol, 351(1): 58–70.
|
|
Seneviratne S I, Stöckli R, 2008. The role of land-atmosphere interactions for climate variability in Europe[C]. Climate Variability and Extremes During the Past 100 years, Switzerland, Springer: 179-193.
https://link.springer.com/chapter/10.1007%2F978-1-4020-6766-2_12 |
|
Shoko C, Clark D, Mengistu M, et al. 2015. Effect of spatial resolution on remote sensing estimation of total evaporation in the uMngeni catchment, South Africa[J]. J Appl Remote Sens, 9(1): 095997.
DOI:10.1117/1.JRS.9.095997 |
|
Sobrino J, El K J, Li Z L. 2003. Surface temperature and water vapour retrieval from MODIS data[J]. Int J Remote Sens, 24(24): 5161–5182.
DOI:10.1080/0143116031000102502 |
|
Su H, McCabe M, Wood E, et al. 2005. Modeling evapotranspiration during SMACEX:Comparing two approaches for local-and regional-scale prediction[J]. J Hydromet, 6(6): 910–922.
DOI:10.1175/JHM466.1 |
|
Su Z. 2002. The Surface Energy Balance System (SEBS) for estimation of turbulent heat fluxes[J]. Hydrol Earth Syst Sci, 6(1): 85–100.
|
|
Su Z, Zhang T, Ma Y, et al. 2006. Energy and water cycle over the Tibetan Plateau:surface energy balance and turbulent heat fluxes[J]. Adv Earth Sci, 21(12): 1224–1236.
|
|
Twine T E, Kustas W, Norman J, et al. 2000. Correcting eddy-covariance flux underestimates over a grassland[J]. Agr Forest Meteor, 103(3): 279–300.
DOI:10.1016/S0168-1923(00)00123-4 |
|
Wilson K, Goldstein A, Falge E, et al. 2002. Energy balance closure at FLUXNET sites[J]. Agr Forest Meteor, 113(1): 223–243.
|
|
Wolf A, Saliendra N, Akshalov K, et al. 2008. Effects of different eddy covariance correction schemes on energy balance closure and comparisons with the modified Bowen ratio system[J]. Agr Forest Meteor, 148(6): 942–952.
|
|
Yang K, Wang J. 2008. A temperature prediction-correction method for estimating surface soil heat flux from soil temperature and moisture data[J]. Sci China, Ser D Earth Sci, 51(5): 721–729.
DOI:10.1007/s11430-008-0036-1 |
|
Zhong L, Ma Y, Salama M S, et al. 2010. Assessment of vegetation dynamics and their response to variations in precipitation and temperature in the Tibetan Plateau[J]. Climat Change, 103(3-4): 519–535.
DOI:10.1007/s10584-009-9787-8 |
|
Zuo H, Xiao X, Yang Q, et al. 2012. On the atmospheric movement and the imbalance of observed and calculated energy in the surface layer[J]. Sci China, Ser D Earth Sci, 55(9): 1518.
DOI:10.1007/s11430-012-4378-3 |
|
丁一汇. 1997. 地表通量的计算问题[J]. 应用气象学报, 8(S1): 29–35.
Ding Y H. 1997. On some aspects of estimates of the surface fluxes[J]. Quart J Appl Meteor, 8(S1): 29–35.
|
|
房云龙, 孙菽芬, 李倩, 等. 2010. 干旱区陆面过程模型参数优化和地气相互作用特征的模拟研究[J]. 大气科学, 34(2): 290–306.
Fang Y L, Sun S F, Li Q, et al. 2010. The optimization of parameters of land surface model in arid region and the simulation of land-atmosphere interaction[J]. Chinese J Atmos Sci, 34(2): 290–306.
DOI:10.3878/j.issn.1006-9895.2010.02.05 |
|
冯璐, 仲雷, 马耀明, 等. 2016. 基于土壤温湿度观测资料估算藏北高原地区土壤热通量[J]. 高原气象, 35(2): 297–308.
Feng L, Zhong L, Ma Y M, et al. 2016. Estimation of soil heat flux over the northern Qinghai-Xizang Plateau based on in-situ soil temperature and moisture data[J]. Plateau Meteor, 35(2): 297–308.
DOI:10.7522/j.issn.1000-0534.2015.00006 |
|
葛骏, 余晔, 李振朝, 等. 2016. 青藏高原多年冻土区土壤冻融过程对地表能量通量的影响研究[J]. 高原气象, 35(3): 608–620.
Ge J, Yu Y, Li Z C, et al. 2016. Impacts of freeze/thaw processes on land surface energy fluxes in the permafrost region of Qinghai-Xizang Plateau[J]. Plateau Meteor, 35(3): 608–620.
DOI:10.7522/j.issn.1000-0534.2016.00032 |
|
黄春林, 李艳, 卢玲, 等. 2014. 考虑干旱水分胁迫的地表通量遥感估算[J]. 水科学进展, 25(2): 181–188.
Huang C L, Li Y, Lu L, et al. 2014. Estimation of surface fluxes under drought water stress conditions based on remotely sensed data[J]. Adv Water Sci, 25(2): 181–188.
|
|
金学杰, 周剑. 2017. 基于SEBS模型和Landsat 8数据的黑河下游蒸散发时空特性分析[J]. 冰川冻土, 39(3): 572–582.
Jin X J, Zhou J. 2017. Analysis of spatial-temporal characteristics of evapotranspiration in the lower reaches of Heihe River based on surface energy balance system model and Landsat 8 data[J]. J Glaciol Geocryol, 39(3): 572–582.
|
|
马耀明, 塚本修, 吴晓鸣, 等. 2000. 藏北高原草甸下垫面近地层能量输送及微气象特征[J]. 大气科学, 24(5): 715–722.
Ma Y M, Osamu T, Wu X M, et al. 2000. Characteristics of energy transfer and micrometeorology in the surface layer of the atmosphere above grassy marshland of the Tibetan Plateau area[J]. Chinese J Atmos Sci, 24(5): 715–722.
DOI:10.3878/j.issn.1006-9895.2000.05.16 |
|
马耀明, 姚檀栋, 王介民, 等. 2006. 青藏高原复杂地表能量通量研究[J]. 地球科学进展, 21(12): 1215–1223.
Ma Y M, Yao T D, Wang J M, et al. 2006. The study on the land surface heat fluxes over heterogeneous landscape of the Tibetan Plateau[J]. Adv Earth Sci, 21(12): 1215–1223.
DOI:10.3321/j.issn:1001-8166.2006.12.002 |
|
马耀明. 2012. 青藏高原多圈层相互作用观测工程及其应用[J]. 中国工程科学, 14(9): 28–34.
Ma Y M. 2012. The observation of water-ice-air-ecosystem interactions and its application over the Tibetan Plateau area[J]. Eng Sci, 14(9): 28–34.
|
|
田辉, 文军, 马耀明, 等. 2009. 夏季黑河流域蒸散发量卫星遥感估算研究[J]. 水科学进展, 20(1): 18–24.
Tian H, Wen J, Ma Y M, et al. 2009. Estimation of summer evapotrauspiration using satellite remote sensing data over the Heihe river basi[J]. Adv Water Sci, 20(1): 18–24.
DOI:10.3321/j.issn:1001-6791.2009.01.003 |
|
王国华, 赵文智. 2011. 遥感技术估算干旱区蒸散发研究进展[J]. 地球科学进展, 26(8): 848–858.
Wang G H, Zhao W Z. 2011. Advances in the application of remote sensing to evapotrauspiration research in arid regions[J]. Adv Earth Sci, 26(8): 848–858.
|
|
王介民, 2012.涡动相关通量观测指导手册[EB/OL]. http://www.hydro-lab.cn/pt/download/woduxiangguantongliangguancezhidaoshouce.pdf.
Wang J M, 2012. Guidelines for making eddy covariance flux measurements[EB/OL]. http://www.hydrolab.cn/pt/download/woduxiangguantongliangguancezhidaoshouce.pdf.
|
|
王介民, 王维真, 奥银焕, 等. 2007. 复杂条件下湍流通量的观测与分析[J]. 地球科学进展, 22(8): 791–797.
Wang J M, Wang W Z, Ao Y H, et al. 2007. Turbulence flux measurements under complicated conditions[J]. Adv Earth Sci, 22(8): 791–797.
DOI:10.3321/j.issn:1001-8166.2007.08.004 |
|
王介民, 王维真, 刘绍民, 等. 2009. 近地层能量平衡闭合问题-综述及个例分析[J]. 地球科学进展, 24(7): 705–713.
Wang J M, Wang W Z, Liu S M, et al. 2009. The problems of surface energy balance closure-an overview and case study[J]. Adv Earth Sci, 24(7): 705–713.
DOI:10.3321/j.issn:1001-8166.2009.07.003 |
|
解晋, 余晔, 刘川, 等. 2018. 青藏高原地表感热通量变化特征及其对气候变化的响应[J]. 高原气象, 37(1): 28–42.
Xie J, Yu Y, Liu C, et al. 2018. Characteristics of surface sensible heat flux over the Qinghai-Tibetan Plateau and its response to climate change[J]. Plateau Meteor, 37(1): 28–42.
DOI:10.7522/j.issn.1000-0534.2016.00032 |
|
杨健, 马耀明. 2012. 青藏高原典型下垫面的土壤温湿特征[J]. 冰川冻土, 34(4): 813–820.
Yang J, Ma Y M. 2012. Soil temperature and moisture features of typical underlying surface in the Tibetan Plateau[J]. J Glaciol Geocryol, 34(4): 813–820.
|
|
叶笃正. 1979. 近年来我国大气科学研究的进展[J]. 大气科学, 3(3): 195–202.
Ye D Z. 1979. Progress of atmospheric science research in China in recent years[J]. Chinese J Atmos Sci, 3(3): 195–202.
DOI:10.3878/j.issn.1006-9895.1979.03.01 |
|
叶笃正, 符淙斌. 1994. 全球变化的主要科学问题[J]. 大气科学, 18(4): 498–512.
Ye D Z, Fu C B. 1994. Major issues of global change sciences[J]. Chinese J Atmos Sci, 18(4): 498–512.
DOI:10.3878/j.issn.1006-9895.1994.04.15 |
|
阳坤, 王介民. 2008. 一种基于土壤温湿资料计算地表土壤热通量的温度预报校正法[J]. 中国科学:D辑, 38(2): 243–250.
Yang K, Wang J M. 2008. A temperature prediction correction method for estimating surface soil heat flux from soil temperature and moisture data[J]. Sci China, ser D Earth Sci, 38(2): 243–250.
|
|
周亚, 高晓清, 李振朝, 等. 2017. 青藏高原深层土壤热通量的变化特征分析[J]. 高原气象, 36(2): 307–316.
Zhou Y, Gao X Q, Li Z C, et al. 2017. Analysis of the characteristics of deep soil heat flux in Qinghai-Tibetan Plateau[J]. Plateau Meteor, 36(2): 307–316.
DOI:10.7522/j.issn.1000-0534.2016.00120 |
|
张长灿, 李栋梁, 王慧, 等. 2017. 青藏高原春季地表感热特征及其对中国东部夏季雨型的影响[J]. 高原气象, 36(1): 13–23.
Zhang C C, Li D L, Wang H, et al. 2017. Characteristics of the surface sensible heat on the Qinghai-Xizang Plateau in the spring and its influences on the summertime rainfall pattern over the Eastern China[J]. Plateau Meteor, 36(1): 13–23.
DOI:10.7522/j.issn.1000-0534.2016.00028 |
2. Institute of Tibetan Plateau Research, Chinese Academy of Sciences, Beijing 100101, China;
3. University of Chinese Academy of Sciences, Beijing 100101, China;
4. Key Laboratory of Tibetan Environment Changes and Land Surface Processes, Chinese Academy of Sciences, Beijing 100101, China;
5. Chinese Academy of Sciences Center for Excellence in Tibetan Plateau Earth Sciences, Beijing 100101, China;
6. Institute of Tropical and Marine Meteorology, China Meteorological Administration, Guangzhou 510080, Guangdong, China
 2018, Vol. 37
2018, Vol. 37
