2. 气象灾害预报预警与评估协同创新中心, 江苏 南京 210044
高原切变线和高原低涡作为青藏高原的特殊天气系统, 会引发青藏高原及其下游地区的暴雨、洪涝等天气灾害, 相关理论研究及应用已有不少(乔全明等, 1984; 隆霄等, 2004; 顾清源等, 2010; 姚秀萍等, 2014; 师锐等, 2011; 李山山等, 2017a)。李国平等(2011)在分析高原低涡的波动特征时, 利用正压原始方程得出高原低涡中包含的波动既有涡旋Rossby波又有惯性重力外波, 涡旋波产生的物理机制为基本气流的垂直涡度发生经向变化所致。马林等(2003)对高原春季成灾的三种天气形势进行了分析, 认为高原切变线对高原低涡形成有重要作用。切变线西南段区域为正涡度区, 上升运动明显, 切变线东北段区域为负涡度区, 也是下沉运动区, 低涡往往在切变线东南侧形成。李子良等(1995)讨论了准地转动量近似下风速切变线上的波动, 导出了切变线上的孤立波解, 对切变线上容易产生低涡给出了一种理论解释。高守亭等(2001)考虑在强涡度存在时切变线已构成一个涡层, 则切变不稳定问题实为涡层不稳定问题。Chen et al(2003)通过模式模拟表明, 正涡度场切变基流与低涡相互作用以及涡块和低涡的合并是直接导致东移低涡强度得以维持和发展的直接原因。李山山等(2017b)在分析高原低涡与高原切变线演变机理时, 引入了分析热带气旋常用的Okubo-Wei参数来表示相对涡度和变形的相对大小, 相对涡度反映低涡强度, 变形量的大小反映的是切变线的强弱, Okubo-Wei参数值的正负则表明了切变线和低涡之间的强弱关系。
综上可见, 高原切变线和高原低涡之间存在密切关系, 高原低涡和高原切变线既是相互独立的系统, 又相互影响和相互伴随, 但两者之间诱发关系并不是很清楚。一种认为高原切变线激发高原低涡(李子良等, 1995; 马林等, 2003; 屠妮妮等, 2010), 另一种认为高原低涡对高原切变线的形成起到了重要作用(高守亭等, 2001), 因此有必要对其两者关系作进一步探讨。本文利用z坐标系下考虑地形坡度的一级近似的正压模式方程组, 探讨高原横切变线上的波动及其不稳定条件, 重点从理论方面初步讨论了切变线和低涡之间的可能联系, 期望能够有助于加深对于“低涡、切变(线)”这一常见高原天气系统组合形式的机理认识。
2 相关定义及物理考虑高原切变线是指500 hPa等压面上, 温度梯度小、三个测站风向对吹的辐合线或两个测站风向对吹且长度大于5个经(纬)距的辐合线(郁淑华, 2013)。高原低涡是指500 hPa等压面上高原地区形成闭合等高线的低压或有3个站点风向呈气旋式的低涡环流(青藏高原气象科学研究拉萨会战组, 1981)。由于目前关于高原切变线与高原低涡关系的研究大多数基于个例分析(屠妮妮, 2010)、统计研究(何光碧, 2009)及数值模拟(Chen et al, 2003), 专门针对高原切变线与高原低涡关系的动力学研究很少。而高原切变线和赤道辐合带(Intertropical Convergence Zone, ITCZ)类似(何光碧, 2013), 高原低涡、西南低涡与热带气旋也有不少相似之处(刘晓冉, 2006)。刘式适(1991)指出, 赤道辐合带是由东北信风和赤道西风构成[图 1(a)], 把它视为东西风风速不连续面[图 1(b)], 在讨论热带气旋发生、发展的不稳定理论中, 统计分析大多数台风发生在赤道辐合带上, 辐合带附近切变很大, 由于切变不稳定, 基本气流的动能转变成涡旋扰动动能, 相当于把台风发生机制转变成讨论赤道辐合带上扰动不稳定性的问题(刘式适, 1991; 谢义炳等, 1964)。郝丽萍等(2016)在研究西南涡暴雨天气过程中, 分析了水平切变线的作用机制, 表明此次暴雨过程是由于水平切变线上扰动不稳定发展形成西南低涡而造成的。王中等(2007)从环流变化角度讨论高原切变线成因可能是新疆地区有高压东移与西太副高西北侧的西南气流之间形成一条东北—西南向的切变线[风场如图 1(c)], 分解后风场如图 1(d)所示。如果仅考虑纬向风的切变而不考虑经向风辐合, 即也可将其视为东西风风速不连续面, 则可以借鉴分析赤道辐合带上热带气旋发生的方法来研究高原切变线与高原低涡或西南低涡的关系。高原横切变线、高原低涡的形成和青藏高原地形密切相关, 而高原地形的动力作用使得西风气流出现绕流和爬坡, 这些都与地形高度和地形坡度的作用有关(何光碧, 2013; 姚秀萍等, 2014), 因此在方程组中有必要考虑地形(坡度)的作用。
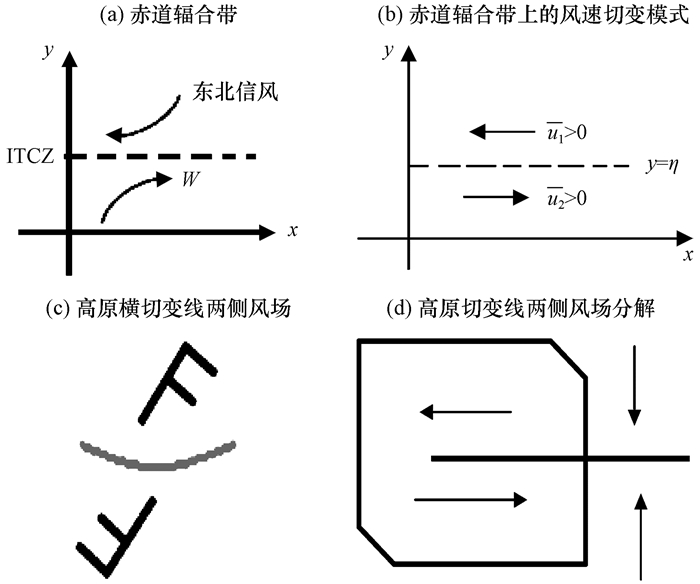
|
图 1 赤道辐合带及高原横切变线两侧风场对比 Fig. 1 Comparison of wind field on both sides of equatorial convergence zone and plateau shear line |
仅考虑纬向风南北切变而形成一条近于纬向的高原切变线, 即高原横切变线, 根据定义其水平尺度一般可视为α中尺度或次天气尺度。设风速切变线的分界面为y0, 切变线南北侧的基本风速分别为
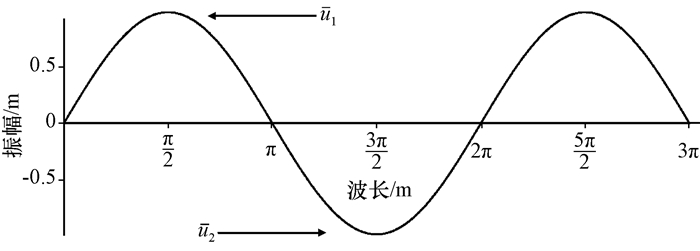
|
图 2 切变波模型示意图 Fig. 2 Schematic diagram of shear wave model |
z坐标系中考虑地形的正压原始模式方程为(刘式适, 2011):
| $ \left\{ \begin{array}{l} \frac{{\partial u}}{{\partial t}} + u\frac{{\partial u}}{{\partial x}} + v\frac{{\partial u}}{{\partial y}} = - \frac{{\partial \phi }}{{\partial x}} + fv\\ \frac{{\partial v}}{{\partial t}} + u\frac{{\partial v}}{{\partial x}} + v\frac{{\partial v}}{{\partial y}} = - \frac{{\partial \phi }}{{\partial y}} - fu\\ \frac{{\partial {\phi ^ * }}}{{\partial t}} + u\frac{{\partial {\phi ^ * }}}{{\partial x}} + v\frac{{\partial {\phi ^ * }}}{{\partial y}} + {\phi ^ * }\left( {\frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}}} \right) = 0 \end{array} \right., $ | (1) |
前两个方程为利用静力学关系和自由面条件简化得到的正压模式水平运动方程, 第三个方程是利用静力学关系和自由面条件简化得到的正压模式连续性方程。其中: ϕ*=ϕ-ϕs; ϕ=gh; ϕs=ghs, hs(x, y)为地形高度, h为上界自由面高度, ϕ为上界自由面位势高度, ϕs为地形位势高度, 其余为常见的物理量符号。
考虑静止大气为背景场(将各变量分解为平均场和扰动场, 即u=u′, v=v′, ϕ=ϕ0+ϕ′; ϕ0=gH=c02, 其中H为静态自由面高度, ϕ0为静态自由面位势高度, 右上角带“'”的均为扰动量), 则式(1)中第三式利用小扰动法线性化后(保留二阶小项)则可以写为:
| $ \begin{array}{l} \frac{{{d_h}\phi '}}{{dt}} - \left( {u\frac{{\partial {\phi _s}}}{{\partial x}} + v\frac{{\partial {\phi _s}}}{{\partial y}}} \right)\\ \;\;\;\;\;\; + \left( {c_0^2 + \phi ' - {\phi _s}} \right)\left( {\frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}}} \right) = 0, \end{array} $ | (2) |
由于高原切变线是α中尺度天气系统, 所以满足Rossby数R0 < 1(于杰等, 2012), 可以视为小参数, 水平运动方程参照李子良等(1995)准地转动量近似下风速切变线上的波动中使用的一级近似方程, 同时式(2)也运用小参数法求得一级近似方程, 其中各量纲为(x, y)=L(x1, y1);
则考虑地形的正压原始方程组的一级近似形式为:
| $ \left\{ \begin{array}{l} \left( {\frac{\partial }{{\partial t}} + {u^{\left( 0 \right)}}\frac{\partial }{{\partial x}} + {v^{\left( 0 \right)}}\frac{\partial }{{\partial y}}} \right){u^{\left( 0 \right)}} - {\beta _0}y{v^{\left( 0 \right)}} - {f_0}{v^{\left( 1 \right)}} = - \frac{{\partial {\phi ^{\left( 1 \right)}}}}{{\partial x}}\\ \left( {\frac{\partial }{{\partial t}} + {u^{\left( 0 \right)}}\frac{\partial }{{\partial x}} + {v^{\left( 0 \right)}}\frac{\partial }{{\partial y}}} \right){v^{\left( 0 \right)}} + {\beta _0}y{u^{\left( 0 \right)}} + {f_0}{u^{\left( 1 \right)}} = - \frac{{\partial {\phi ^{\left( 1 \right)}}}}{{\partial y}}\\ \left( {\frac{\partial }{{\partial t}} + {u^{\left( 0 \right)}}\frac{\partial }{{\partial x}} + {v^{\left( 0 \right)}}\frac{\partial }{{\partial y}}} \right){\phi ^{\left( 0 \right)}} + c_0^2\left( {\frac{{\partial {u^{\left( 1 \right)}}}}{{\partial x}} + \frac{{\partial {v^{\left( 1 \right)}}}}{{\partial y}}} \right) = {u^{\left( 0 \right)}}\frac{{\partial {\phi _s}}}{{\partial x}} + {v^{\left( 0 \right)}}\frac{{\partial {\phi _s}}}{{\partial y}} \end{array} \right., $ | (3) |
考虑纬向气流准地转, 经向气流非地转, 对切变线上扰动采用半地转近似(仅考虑ϕs是y的函数, 且
| $ \left\{ \begin{array}{l} \left( {\frac{\partial }{{\partial t}} + \overline {{u_j}} \frac{\partial }{{\partial x}}} \right){u_{gj}} - {\beta _0}y{v_{gj}} - {f_0}{v_j} = - \frac{{\partial {\phi _j}}}{{\partial x}}\\ \left( {\frac{\partial }{{\partial t}} + \overline {{u_j}} \frac{\partial }{{\partial x}}} \right){v_{gj}} + {\beta _0}y{u_{gj}} + {f_0}{u_j} = - \frac{{\partial {\phi _j}}}{{\partial y}}\\ \left( {\frac{\partial }{{\partial t}} + \overline {{u_j}} \frac{\partial }{{\partial x}}} \right){\phi _j} + c_0^2\left( {\frac{{\partial {u_j}}}{{\partial x}} + \frac{{\partial {v_j}}}{{\partial y}}} \right) = {v_{gj}}\frac{{d{\phi _s}}}{{dy}} \end{array} \right., $ | (4) |
式中: j=1, 2, 分别表示分界面以北、以南的各物理量场。
由式(4)整理得:
| $ \begin{array}{l} \left( {\frac{\partial }{{\partial t}} + {{\bar u}_j}\frac{\partial }{{\partial x}}} \right){\zeta _{gj}} + {\beta _0}{v_{gj}}\\ \;\;\;\;\;\;\;\; = - \frac{{{f_0}}}{{c_0^2}}\left[ {{v_{gj}}\frac{{d{\phi _s}}}{{dy}} - \left( {\frac{\partial }{{\partial t}} + {{\bar u}_j}\frac{\partial }{{\partial x}}} \right){\phi _j}} \right], \end{array} $ | (5) |
式中:
在气流分界面上, 取位势场(相当于气压场)连续的条件, 则风速切变线上的动力学边界条件为:
| $ \begin{array}{l} \left( {\frac{\partial }{{\partial t}} + {{\bar u}_j}\frac{\partial }{{\partial x}}} \right)\left( {{\phi _1} - {\phi _2}} \right) + {v_j}\frac{\partial }{{\partial y}}\left( {\overline {{\phi _1}} - \overline {{\phi _2}} } \right) = 0,\\ y = {y_o}\;时, \end{array} $ | (6) |
y=yo时,
取南北两侧的自然边界条件为:
| $ \left\{ {\begin{array}{*{20}{c}} {y \to - \infty ,\;\;\;\;\;{\phi _1} \to 0}\\ {y \to \infty ,\;\;\;\;\;{\phi _2} \to 0} \end{array}} \right. $ | (7) |
因为基本重力位势高度满足地转关系, 即:
| $ \frac{{\partial \overline {{\phi _1}} }}{{\partial y}} = - {f_1}\overline {{u_1}} ,\frac{{\partial \overline {{\phi _2}} }}{{\partial y}} = - {f_2}\overline {{u_2}} , $ | (8) |
则描述风速切变线上的内边界条件式(6)可以转换为:
| $ \begin{array}{l} y = {y_0}\;时,\\ \left( {\frac{\partial }{{\partial t}} + {{\bar u}_j}\frac{\partial }{{\partial x}}} \right)\left( {{\phi _1} - {\phi _2}} \right) - \left( {{f_1}\overline {{u_1}} - {f_2}\overline {{u_2}} } \right){v_j} = 0, \end{array} $ | (9) |
因为地转涡度和地转风与重力位势的关系为:
| $ \begin{array}{*{20}{c}} {{v_{gj}} = \frac{1}{{{f_0}}}\frac{{\partial {\phi _j}}}{{\partial x}},{u_{gj}} = - \frac{1}{{{f_0}}}\frac{{\partial {\phi _j}}}{{\partial y}}}\\ {{\zeta _{gj}} = \frac{{\partial {v_{gj}}}}{{\partial x}} - \frac{{\partial {u_{gj}}}}{{\partial y}} = \frac{1}{{{f_0}}}{\nabla ^2}{\phi _j}} \end{array}, $ | (10) |
由方程组(5)结合式(10)可得:
| $ \begin{array}{l} \left( {\frac{\partial }{{\partial t}} + \overline {{u_j}} \frac{\partial }{{\partial x}}} \right)\left[ {{\nabla ^2}{\phi _j} - \frac{{f_0^2}}{{c_0^2}}{\phi _j}} \right] + {\beta _0}\frac{{\partial {\phi _j}}}{{\partial x}}\\ \;\;\;\;\;\;\; = - \frac{{{f_0}}}{{c_0^2}}\frac{{d{\phi _s}}}{{dy}}\frac{{\partial {\phi _j}}}{{\partial x}}, \end{array} $ | (11) |
假设方程(11)有如下形式的波动解:
| $ {\phi _j} = {\mathit{\Phi }_j}\left( y \right){e^{ik\left( {x - ct} \right)}}, $ | (12) |
将式(12)代入到式(11), 在uj-c≠0时有:
| $ \frac{{{d^2}{\mathit{\Phi }_j}}}{{d{y^2}}} - \left[ {{k^2} + \frac{{f_0^2}}{{c_0^2}} - \frac{{{\beta _0}}}{{\overline {{u_j}} - c}} - \frac{{{f_0}\frac{{d{\phi _s}}}{{dy}}}}{{c_0^2\left( {\overline {{u_j}} - c} \right)}}} \right]{\mathit{\Phi }_j} = 0, $ | (13) |
令
| $ \left\{ \begin{array}{l} {\mathit{\Phi }_1}\left( y \right) = A{e^{\sqrt {{\alpha _1}} y}} + {C^{ - \sqrt {{\alpha _1}} y}}\\ {\mathit{\Phi }_2}\left( y \right) = D{e^{\sqrt {{\alpha _2}} y}} + {B^{ - \sqrt {{\alpha _2}} y}} \end{array} \right., $ | (14) |
根据自然边界条件式(7)得:
| $ \left\{ \begin{array}{l} {\phi _1} = A{e^{\sqrt {{\alpha _1}} y}}{e^{ik\left( {x - ct} \right)}}\\ {\phi _2} = {B^{ - \sqrt {{\alpha _2}} y}}{e^{ik\left( {x - ct} \right)}} \end{array} \right., $ | (15) |
将式(12)带入方程(4)的第一式可得:
| $ {v_j} = ik{f_0}^{ - 2}\left[ {\left( {{f_0} - {\beta _o}y} \right){\phi _j} - \left( {\overline {{u_j}} - c} \right)\frac{{\partial {\phi _j}}}{{\partial y}}} \right], $ | (16) |
将式(15)和(16)带入内边界条件式(9), 在y=y0处得到:
| $ \left\{ \begin{array}{l} \left[ {{f_0}\left( {\overline {{u_1}} - c} \right) + \left( {\overline {{u_2}} - \overline {{u_1}} } \right)\left( {{f_0} - {\beta _0}y} \right) -\\ \left( {\overline {{u_2}} - \overline {{u_1}} } \right)\left( {\overline {{u_1}} - c} \right)\sqrt {{\alpha _1}} } \right]A{e^{\sqrt {{\alpha _1}} y}} - {f_0}\left( {\overline {{u_1}} - c} \right)B{e^{ - \sqrt {{\alpha _2}} y}} = 0\\ {f_0}\left( {\overline {{u_2}} - c} \right)A{e^{\sqrt {{\alpha _1}} y}} + \left[ {{f_0}\left( {\overline {{u_2}} - c} \right) + \left( {\overline {{u_2}} - \overline {{u_1}} } \right)\left( {{f_0} - {\beta _0}y} \right) +\\ \left( {\overline {{u_2}} - \overline {{u_1}} } \right)\left( {\overline {{u_2}} - c} \right)\sqrt {{\alpha _2}} } \right]B{e^{ - \sqrt {{\alpha _2}} y}} = 0 \end{array} \right., $ | (17) |
式(16)为系数A、B的齐次线性方程组, 有非零解的条件为:
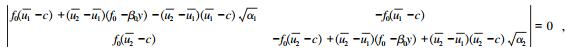
|
(18) |
其解为:
| $ c = \frac{{2\overline {{u_2}} {f_0}\sqrt {{\alpha _2}} + 2\overline {{u_1}} {f_0}\sqrt {{\alpha _1}} - \left( {\overline {{u_2}} - \overline {{u_1}} } \right)\left( {\overline {{u_2}} + \overline {{u_1}} } \right)\sqrt {{\alpha _1}{\alpha _2}} \pm \sqrt {{{\left( {\overline {{u_2}} - \overline {{u_1}} } \right)}^2}\sqrt {{\alpha _1}{\alpha _2}} \left[ {\sqrt {{\alpha _1}{\alpha _2}} {{\left( {\overline {{u_2}} - \overline {{u_1}} } \right)}^2} - 4f_0^2} \right]} }}{{2\left[ {{f_0}\sqrt {{\alpha _2}} + {f_0}\sqrt {{\alpha _1}} - \left( {\overline {{u_2}} - \overline {{u_1}} } \right)\sqrt {{\alpha _1}{\alpha _2}} } \right]}}, $ | (19) |
式(19)表示的即为由于切变线两侧纬向风速切变导致的分界面上产生的波动。从中可以分析出高原切变线引起的波动包括切变波、惯性波和重力外波, 本文将其统称为地形切变波(下同)。该波动是双向传播的频散波, 波速与基本气流和基本气流切变有关, 还与科里奥利参数f0、牛顿声速c02、地形坡度
由于式(19)中的
该切变波的不稳定性取决于(
参考刘式适等(1988, 2000)在讨论青藏高原大地形作用下Rossby波的分析方法, 以方程组(3)为基础且考虑地形坡度, 由于零级近似满足水平无辐合辐散, 则引入速度流函数后有:
| $ \left\{ \begin{array}{l} \left( {\frac{\partial }{{\partial t}} + {u^{\left( 0 \right)}}\frac{\partial }{{\partial x}} + {v^{\left( 0 \right)}}\frac{\partial }{{\partial y}}} \right)\left( {f + {\zeta ^{\left( 0 \right)}}} \right) = - {f_0}D\\ \left( {\frac{\partial }{{\partial t}} + {u^{\left( 0 \right)}}\frac{\partial }{{\partial x}} + {v^{\left( 0 \right)}}\frac{\partial }{{\partial y}}} \right)\left( {{f_0}\psi } \right) = - c_0^2D + \frac{{\partial \psi }}{{\partial x}}\frac{{d{\phi _s}}}{{dy}} \end{array} \right., $ | (20) |
式中:
由式(20)得:
| $ \begin{array}{l} \left( {\frac{\partial }{{\partial t}} + {u^{\left( 0 \right)}}\frac{\partial }{{\partial x}} + {v^{\left( 0 \right)}}\frac{\partial }{{\partial y}}} \right)\left( {f + {\zeta ^{\left( 0 \right)}} - \lambda _0^2\psi } \right)\\ \;\;\;\;\;\;\; + \frac{{{f_0}}}{{c_0^2}}\frac{{\partial \psi }}{{\partial x}}\frac{{d{\phi _s}}}{{dy}} = 0, \end{array} $ | (21) |
式中:
令q=f+ζ(0)-λ02ψ=f+
| $ \left( {\frac{\partial }{{\partial t}} + {u^{\left( 0 \right)}}\frac{\partial }{{\partial x}} + {v^{\left( 0 \right)}}\frac{\partial }{{\partial y}}} \right)q + \frac{{{f_0}}}{{c_0^2}}\frac{{\partial \psi }}{{\partial x}}\frac{{d{\phi _s}}}{{dy}} = 0, $ | (22) |
将式(22)进行线性化, 即设u=u+u′, v=v′, q=+q′, 得:
| $ \frac{{\partial q'}}{{\partial t}} + \bar u\frac{{\partial q'}}{{\partial x}} + v'\frac{{\partial \bar q}}{{\partial y}} + \frac{{{f_0}}}{{c_0^2}}\frac{{\partial \psi '}}{{\partial x}}\frac{{d{\phi _s}}}{{dy}} = 0, $ | (23) |
其中:
式(23)可改写成:
| $ \begin{array}{l} \left( {\frac{\partial }{{\partial t}} + \bar u\frac{\partial }{{\partial x}}} \right)\left( {\nabla _h^2\psi ' - \lambda _0^2\psi '} \right) + \\ \;\;\;\;\;\;\;\;\frac{{\partial \psi '}}{{\partial x}}\left( {{\beta _0} - \frac{{{\partial ^2}\bar u}}{{\partial {y^2}}} + \lambda _0^2\bar u + \frac{{{f_0}}}{{c_0^2}}\frac{{d{\phi _s}}}{{dy}}} \right) = 0, \end{array} $ | (24) |
把ψ′=
| $ \frac{{{d^2}\varphi }}{{d{y^2}}} - \left( {{k^2} + {\lambda _0} - \frac{{{\beta _0} - \frac{{{\partial ^2}\bar u}}{{\partial {y^2}}} + \lambda _0^2\bar u + \frac{{{f_0}}}{{c_0^2}}\frac{{d{\phi _s}}}{{dy}}}}{{\bar u - c}}} \right)\varphi = 0, $ | (25) |
令c=cr+ici;
| $ \begin{array}{*{20}{c}} {\frac{{{d^2}{\varphi _r}}}{{d{y^2}}} - \left[ {{k^2} + \lambda _0^2 - \left( {{\beta _0} - \frac{{{\partial ^2}\bar u}}{{\partial {y^2}}} + \lambda _0^2\bar u + \frac{{{f_0}}}{{c_0^2}}\frac{{d{\phi _s}}}{{dy}}} \right){\delta _r}} \right]{\varphi _r}}\\ { - \left( {{\beta _0} - \frac{{{\partial ^2}\bar u}}{{\partial {y^2}}} + \lambda _0^2\bar u + \frac{{{f_0}}}{{c_0^2}}\frac{{d{\phi _s}}}{{dy}}} \right){\delta _i}{\varphi _i} = 0,} \end{array} $ | (26) |
| $ \begin{array}{*{20}{c}} {\frac{{{d^2}{\varphi _i}}}{{d{y^2}}} - \left[ {{k^2} + \lambda _0^2 - \left( {{\beta _0} - \frac{{{\partial ^2}\bar u}}{{\partial {y^2}}} + \lambda _0^2\bar u + \frac{{{f_0}}}{{c_0^2}}\frac{{d{\phi _s}}}{{dy}}} \right){\delta _r}} \right]{\varphi _i}}\\ { + \left( {{\beta _0} - \frac{{{\partial ^2}\bar u}}{{\partial {y^2}}} + \lambda _0^2\bar u + \frac{{{f_0}}}{{c_0^2}}\frac{{d{\phi _s}}}{{dy}}} \right){\delta _i}{\varphi _r} = 0,} \end{array} $ | (27) |
| $ i{c_i}\int_{{y_1}}^{{y_2}} {\left( {{\beta _0} - \frac{{{\partial ^2}\bar u}}{{\partial {y^2}}} + \lambda _0^2\bar u + \frac{{{f_0}}}{{c_0^2}}\frac{{d{\phi _s}}}{{dy}}} \right)\frac{{{{\left| \varphi \right|}^2}}}{{{{\left| {\bar u - c} \right|}^2}}}{\rm{d}}y} = 0, $ | (28) |
如果扰动是不稳定的(ci≠0), 则必有:
| $ \int_{{y_1}}^{{y_2}} {\left( {{\beta _0} - \frac{{{\partial ^2}\bar u}}{{\partial {y^2}}} + \lambda _0^2\bar u + \frac{{{f_0}}}{{c_0^2}}\frac{{d{\phi _s}}}{{dy}}} \right)\frac{{{{\left| \varphi \right|}^2}}}{{{{\left| {\bar u - c} \right|}^2}}}{\rm{d}}y} = 0, $ | (29) |
上式要成立, 忽略β0(因为切变线为中尺度系统), 得到波动不稳定条件是在区间(y1, y2)内, 至少有一点满足如下条件:
| $ \left( { - \frac{{{\partial ^2}\bar u}}{{\partial {y^2}}} + \lambda _0^2\bar u + \frac{{{f_0}}}{{c_0^2}}\frac{{d{\phi _s}}}{{dy}}} \right) = 0, $ | (30) |
尽管物理考虑与数学处理方法不同, 但式(30)与伍荣生(1964, 1982)和吕克利(1986a, 1986b)所得结果是一致的。对式(30)的物理意义可做如下讨论:
当不考虑地形坡度且为均匀的西风基流或东风基流时, 叠加在基本气流上的扰动总是稳定的, 由此也可看出切变气流和地形坡度对激发扰动不稳定的重要性。由于O(λ02u)~10-12 m-1·s-1,
对于
对于切变基流
由以上几点讨论可见, 地形坡度对波动不稳定贡献的大小取决于基本气流的纬向分布状况。
4 不考虑地形坡度时的切变波在波速表达式(19)中, 如果不考虑地形南北坡度
| $ c = \frac{{2\overline {{u_2}} {f_0}k + 2\overline {{u_1}} {f_0}k - \left( {\overline {{u_2}} - \overline {{u_1}} } \right)\left( {\overline {{u_2}} + \overline {{u_1}} } \right){k^2} \pm \sqrt {{{\left( {\overline {{u_1}} - \overline {{u_2}} } \right)}^2}{k^2}\left[ {{k^2}{{\left( {\overline {{u_1}} - \overline {{u_2}} } \right)}^2} - 4f_0^2} \right]} }}{{4{f_0}k - 2\left( {\overline {{u_2}} - \overline {{u_1}} } \right){k^2}}}. $ | (31) |
当
通过式(31)可得波动稳定性判据为:
| $ {\left( {\overline {{u_1}} - \overline {{u_2}} } \right)^2}{k^2}\left[ {{k^2}{{\left( {\overline {{u_1}} - \overline {{u_2}} } \right)}^2} - 4f_0^2} \right]\left\{ {\begin{array}{*{20}{c}} \begin{array}{l} > 0,\\ = 0,\\ < 0, \end{array}&\begin{array}{l} 波动稳定\\ 中性\\ 波动不稳定 \end{array} \end{array}} \right. $ | (32) |
由式(32)所示波动稳定性判据的中性情况, 可得波动处于临界状态时:
| $ {\left( {\overline {{u_1}} - \overline {{u_2}} } \right)^2}{k^2}\left[ {{k^2}{{\left( {\overline {{u_1}} - \overline {{u_2}} } \right)}^{20}} - 4f_0^2} \right] = 0, $ | (33) |
从而得到临界波数:
| $ {k_c} = \frac{{2{f_0}}}{{\left| {\overline {{u_1}} - \overline {{u_2}} } \right|}}, $ | (34) |
当k>kc时, 波动是稳定的; 当k < kc, 波动才可能不稳定发展。
当水平风切变呈气旋性旋转时(即
| $ \overline {{u_2}} - \overline {{u_1}} < \frac{{2{f_0}}}{k}, $ | (35) |
即切变线上扰动不稳定与基本气流切变的大小、波数和所处纬度有关。
同样, 可得临界波长:
| $ {L_c} = \frac{{2\pi }}{{{k_c}}} = \frac{{\pi \left| {\overline {{u_1}} - \overline {{u_2}} } \right|}}{{{f_0}}}, $ | (36) |
当L < Lc, 波动是稳定的; 当L>Lc, 波动才可能不稳定发展。
上述讨论表明如果基流存在南北切变, 切变线上波长较长的波易发生不稳定而得以优先发展。
4.2.3 波动不稳定增长率波动处于不稳定状态时, 波速
| $ \begin{array}{*{20}{c}} {c = \frac{{2\overline {{u_2}} {f_0}k + 2\overline {{u_2}} {f_0}k - \left( {\overline {{u_2}} - \overline {{u_1}} } \right)\left( {\overline {{u_2}} + \overline {{u_1}} } \right){k^2}}}{{4{f_0}k - 2{{\left( {\overline {{u_2}} - \overline {{u_1}} } \right)}k^2}}}}\\ { \pm \mathit{\boldsymbol{i}}\sqrt {\frac{{\left( {\overline {{u_1}} - \overline {{u_2}} } \right){k^2}\left[ {4{f_0}k - 2{{\left( {\overline {{u_1}} - \overline {{u_2}} } \right)}^2}} \right]}}{{\left[ {4{f_0} - 2\left( {\overline {{u_2}} - \overline {{u_1}} } \right){k^2}} \right]}}} ,} \end{array} $ | (37) |
则波动不稳定增长率为:
| $ \left| {k{c_i}} \right| = \sqrt {\frac{{\left( {\overline {{u_1}} - \overline {{u_2}} } \right){k^2}\left[ {4{f_0}k - 2{{\left( {\overline {{u_1}} - \overline {{u_2}} } \right)}^2}} \right]}}{{\left[ {4{f_0} - 2\left( {\overline {{u_2}} - \overline {{u_1}} } \right){k^2}} \right]}}} , $ | (38) |
综合上文的讨论可以看出, 有利于切变波不稳定发展的条件有:基流南北切变或南北辐合要强, 扰动系统的水平尺度要比较大。
4.3 波动不稳定的必要条件为明确切变波不稳定与涡旋波不稳定之间的关系, 下面我们用类似于正压不稳定的分析方法进行以下讨论。
4.3.1 切变波不稳定的必要条件与上文考虑地形坡度时讨论切变波不稳定必要条件的方法类似, 此时不考虑地形坡度, 考虑水平辐合辐散, 引入速度流函数有:
| $ \left\{ \begin{array}{l} \left( {\frac{\partial }{{\partial t}} + {u^{\left( 0 \right)}}\frac{\partial }{{\partial x}} + {v^{\left( 0 \right)}}\frac{\partial }{{\partial y}}} \right)\left( {f + {\zeta ^{\left( 0 \right)}}} \right) = - {f_0}D\\ \left( {\frac{\partial }{{\partial t}} + {u^{\left( 0 \right)}}\frac{\partial }{{\partial x}} + {v^{\left( 0 \right)}}\frac{\partial }{{\partial y}}} \right)\left( {{f_0}\psi } \right) = - c_0^2D \end{array} \right., $ | (39) |
如果扰动是不稳定的(ci≠0), 则有:
| $ \int_{{y_1}}^{{y_2}} {\left( {{\beta _0} - \frac{{{\partial ^2}\bar u}}{{\partial {y^2}}} + \lambda _0^2\bar u} \right)\frac{{{{\left| \varphi \right|}^2}}}{{{{\left| {\bar u - c} \right|}^2}}}dy} = 0, $ | (40) |
上式若要成立, 在区间(y1, y2)内必有:
| $ \left( {{\beta _0} - \frac{{{\partial ^2}\bar u}}{{\partial {y^2}}} + \lambda _0^2\bar u} \right) = 0, $ | (41) |
忽略β0后得到波动不稳定条件是在区间内至少有一点满足:
| $ \frac{{{\partial ^2}\bar u}}{{\partial {y^2}}} - \lambda _0^2\bar u = 0, $ | (42) |
由上式可知在纬向基流呈波动型(u=C1eλ0y+C2e-λ0y)分布时, 更有利于切变波不稳定发展。
4.3.2 涡旋波不稳定的必要条件为讨论有利于涡旋波不稳定发展的形式, 讨论的数学方程组依旧为式(3), 在涡层内主要考虑涡度, 即假定扰动水平无辐合辐散, 即方程式(3)中水平散度项D=0, 则讨论的方程变为:
| $ \left( {\frac{\partial }{{\partial t}} + {u^{\left( 0 \right)}}\frac{\partial }{{\partial x}} + {v^{\left( 0 \right)}}\frac{\partial }{{\partial y}}} \right)\left( {f + {\zeta ^{\left( 0 \right)}}} \right) = 0, $ | (43) |
各符号代表物理量与上述一致, 为便于与不考虑地形坡度时切变波不稳定的必要条件对比, 依旧令绝对涡度ζa=f+ζ(0)=f+
| $ \left( {\frac{\partial }{{\partial t}} + {u^{\left( 0 \right)}}\frac{\partial }{{\partial x}} + {v^{\left( 0 \right)}}\frac{\partial }{{\partial y}}} \right){\zeta _{\rm{a}}} = 0, $ | (44) |
将式(44)进行线性化, u=u+u′, v=v′, ζa=
| $ \left( {\frac{\partial }{{\partial t}} + \bar u\frac{\partial }{{\partial x}}} \right)\nabla _h^2\psi ' + \frac{{\partial \psi '}}{{\partial x}}\left( {{\beta _0} - \frac{{\partial \bar u}}{{\partial {y^2}}}} \right) = 0, $ | (45) |
类似长波正压不稳定的讨论可得:
| $ i{c_i}\int_{{y_1}}^{{y_2}} {\left( {{\beta _0} - \frac{{{\partial ^2}\bar u}}{{\partial {y^2}}}} \right)\frac{{{{\left| \varphi \right|}^2}}}{{{{\left| {\bar u - c} \right|}^2}}}{\rm{d}}y} = 0, $ | (46) |
如果扰动是不稳定的(ci≠0), 则应有:
| $ \int_{{y_1}}^{{y_2}} {\left( {{\beta _0} - \frac{{{\partial ^2}\bar u}}{{\partial {y^2}}}} \right)\frac{{{{\left| \varphi \right|}^2}}}{{{{\left| {\bar u - c} \right|}^2}}}{\rm{d}}y} = 0, $ | (47) |
上式要成立, 在区间(y1, y2)内至少有一点必有:
| $ \left( {{\beta _0} - \frac{{{\partial ^2}\bar u}}{{\partial {y^2}}}} \right) = 0, $ | (48) |
忽略β0, 得到涡旋波波动不稳定条件是在区间内, 至少有一点满足:
| $ \frac{{{\partial ^2}\bar u}}{{\partial {y^2}}} = 0. $ | (49) |
结合切变波不稳定必要条件的讨论和关于涡旋波不稳定必要条件的讨论, 结合式(42)和式(49)可以看出, 切变波不稳定和涡旋波不稳定之间有一定联系。
根据量纲分析来看, 由于
本文分析主要针对风呈气旋性切变形成的横切变线, 即在切变线以北基本气流是东风基流(u < 0), 切变线以南基本气流是西风基流(u>0)。在切变线以南如果基本气流分布满足
从以上分析可以看出, 切变线位置与
由以上讨论可知, 地形坡度对切变线上波动稳定性的贡献主要取决于基本气流的纬向分布状况。为简单起见, 用基本气流的纬向分布状况来反映地形坡度对切变线上波动不稳定发展和低涡形成的作用。切变线发生的位置一般与
从环流形势分析来看, 500 hPa东亚地区中纬度环流为“一槽一脊”型[图 3, 该图及文中所涉及的地图是基于国家测绘地理信息局标准地图服务网站下载的审图号为GS(2016)1579号的标准地图制作, 底图无修改], 宽脊内有较多短波槽脊活动, 乌拉尔山东侧的西风槽加深发展, 槽底的西风带在高原的大地形作用下分为南北两支, 形成南北绕流形势。槽底梯度逐渐加大, 西风加速, 南支槽加深东移, 槽前高原南部的西南风加强, 从新疆到内蒙古为长波脊区, 同时注意到青海附近的浅脊有所发展, 对应风场上为一反气旋环流, 其辐散出的东北风在西藏北部与槽前高原南部的西南风辐合, 形成高原切横变线。由于槽底西风加强, 南支槽加深, 高原南部逐渐加强的西南风, 与青海附近逐渐加强的反气旋辐散出的东北风产生更强的辐合, 切变线发展加强逐渐演变形成一气旋性低涡。
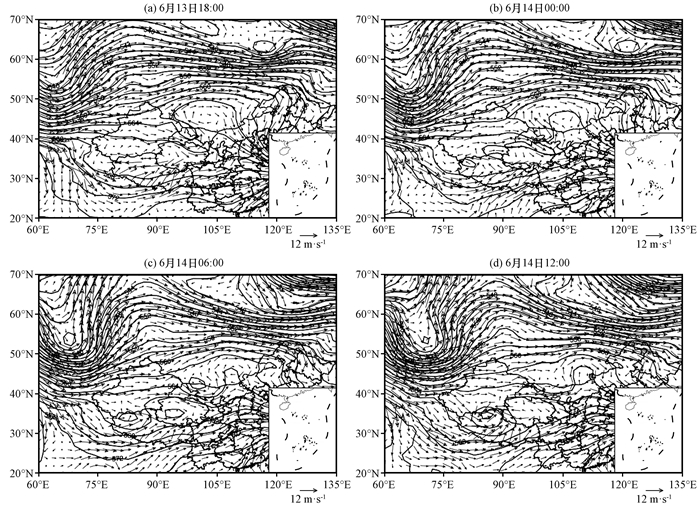
|
图 3 2015年6月13-14日500 hPa位势高度场(等值线, 单位: dagpm)和风场(矢量, 单位: m·s-1)分布 Fig. 3 The geopotential height field (contour, unit: dagpm) and wind field (vector, unit: m·s-1) at 500 hPa during the period of 13-14 June 2015 |
图 4为2015年6月13-14日流场和纬向基流二阶切变
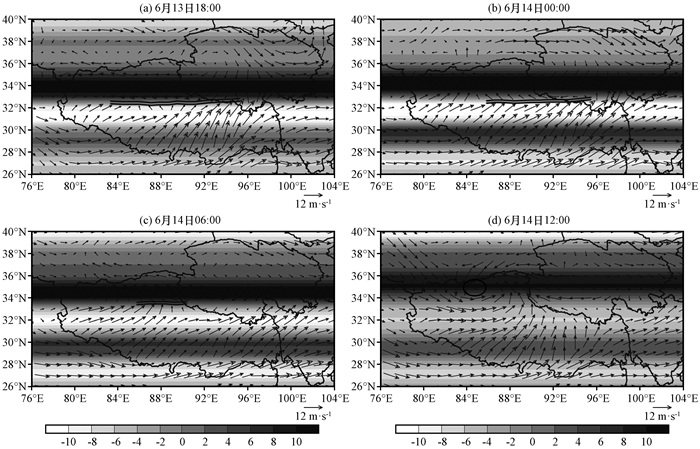
|
图 4 2015年6月13-14日500 hPa风速的二阶切变项(阴影区, 单位: ×10-11s-2)和风场(矢量, 单位: m·s-1)分布 黑色实线代表高原切变线, 黑色圆圈代表高原低涡中心 Fig. 4 The distribution of second order shear (the shaded, unit: ×10-11s-2) and wind field (vector, unit: m·s-1) at 500 hPa from 13 to 14 June 2015. The black line represents the plateau shear line, and the black circle represents the center of the plateau vortex |
从动力学视角利用一级近似的正压模式方程组, 分析了地形南北坡度对切变线上波动的影响以及高原切变线与高原低涡之间的可能联系, 得到以下几点理论认识:
(1) 包含地形坡度的切变波是双向传播的频散波, 波速与基本气流和基本气流的南北切变有关, 还与地形坡度以及波数有关。切变线上波动的不稳定性与波数有关, 波数较小(波长较长)的波动易于不稳定发展。
(2) 地形坡度对波动不稳定性的贡献大小取决于基本气流的纬向分布状况。对于南北均匀的纬向基流或具有线性切变的基流, 地形坡度对波动的不稳定性起主要作用, 总是有利于地形切变线上的扰动不稳定发展。
(3) 涡旋波是切变波的一种特殊形式, 切变波不稳定可激发涡旋波不稳定。即切变线会激发与基流切变有关的切变波, 而在一定条件下切变波不稳定又会诱发涡旋波不稳定。则高原切变线上扰动不稳定发展可促使高原低涡发生、发展, 两者有密切联系。
本文分析方法及结果对认识高原切变线上的波动以及切变线与低涡之间的关系有一定理论意义, 但在讨论切变线风场时仅考虑了纬向风的切变, 对经向风的辐合尚未考虑; 理论应用于天气实践的个例还较少。此外, 切变波与涡旋波之间如何相互作用与相互转换, 高原切变线、切变线上波动、高原低涡之间联系的完整建立, 这些问题的解决有待今后研究中通过理论完善、数值试验及更多应用检验等路径不断向前推进。
Chen G, Li G P. 2014. Dynamic and numerical study of waves in the Tibetan Plateau vortex[J]. Adv Atmos Sci, 31(1): 131–138.
|
|
Chen L S, Luo Z X. 2003. A preliminary study of the dynamics of eastward shifting cyclonic vortices[J]. Adv Atmos Sci, 20(3): 323–332.
|
|
高守亭, 周玉淑. 2001. 水平切变线上涡层不稳定理论[J]. 气象学报, 59(4): 393–404.
Gao S T, Zhou Y S. 2001. The instability of the vortex sheet along the shear line[J]. Acta Meteor Sinica, 59(4): 393–404.
|
|
顾清源, 师锐, 徐会明. 2010. 移出与未移出高原的两类低涡环流特征的对比分析[J]. 气象, 36(4): 7–15.
Gu Q Y, Shi R, Xu H M. 2010. Comparison analysis of the circulation characteristics of plateau vortex moving out of and not out of the plateau[J]. Meteor Mon, 36(4): 7–15.
|
|
郝丽萍, 周瑾, 康岚. 2016. 西南涡暴雨天气过程分析和数值模拟试验[J]. 高原气象, 35(5): 1182–1190.
Hao L P, Zhou J, Kang L. 2016. Weather analyses and numerical study of Southwest China vortex and its induced heavy rainfall[J]. Plateau Meteor, 35(5): 1182–1190.
DOI:10.7522/j.issn.1000-0534.2015.00046 |
|
何光碧. 2013. 高原切变线研究回顾[J]. 高原山地气象研究, 33(1): 90–96.
He G B. 2013. Review of the plateau shear-line studies[J]. Plateau Mountain Meteor Res, 33(1): 90–96.
DOI:10.3969/j.issn.1674-2184.2013.01.016 |
|
何光碧, 高文良, 屠妮妮. 2009. 2000-2007年夏季青藏高原低涡切变线观测事实分析[J]. 高原气象, 28(3): 549–555.
He G B, Gao W L, Tu N N. 2009. The observational analysis of shear line and low vortex over the Tibetan Plateau in summer from 2000 to 2007[J]. Plateau Meteor, 28(3): 549–555.
|
|
李国平, 罗喜平, 陈婷, 等. 2011. 高原低涡中涡旋波动特征的初步分析[J]. 高原气象, 30(3): 553–558.
Li G P, Luo X P, Chen T, et al. 2011. Preliminary theorotical study of waves in the Tibetan Plateau vortex[J]. Plateau Meteor, 30(3): 553–558.
|
|
李山山, 李国平. 2017a. 一次高原低涡与高原切变线演变过程与机理分析[J]. 大气科学, 41(4): 713–726.
Li S S, Li G P. 2017a. Evolution and mechanism analysis of a plateau vortex and plateau shear line[J]. Chinese J Atmos Sci, 41(4): 713–726.
DOI:10.3878/j.issn.1006-9895.1611.16179 |
|
李山山, 李国平. 2017b. 一次鞍型场环流背景下高原东部切变线降水的湿Q矢量诊断分析[J]. 高原气象, 36(2): 317–329.
Li S S, Li G P. 2017b. Diagnostic analysis based on wet Q-vector of a shear line with rain on the east side of Qinghai-Tibetan Plateau under the saddle pattern circulation background field[J]. Plateau Meteor, 36(2): 317–329.
DOI:10.7522/j.issn.1000-0534.2016.00025 |
|
李子良, 万军. 1995. 准地转动量近似下风速切变线上的波动[J]. 气象学报, 53(3): 289–298.
Li Z L, Wan J. 1995. Stability of the nonlinear waves on the horizontal shear-line of wind with the geostrophic momentum approximation[J]. Acta Meteor Sinica, 53(3): 289–298.
DOI:10.3321/j.issn:0577-6619.1995.03.007 |
|
刘式适. 1991. 热带气旋发生、发展的不稳定理论[J]. 热带海洋学报, 10(2): 1–9.
Liu S S. 1991. Unstable theory on the formation and development of tropical cyclone[J]. J Trop Ocean, 10(2): 1–9.
|
|
刘式适, 柏晶瑜, 陈华. 2000. 青藏高原大地形作用下的Rossby波[J]. 高原气象, 19(3): 331–338.
Liu S S, Bai J Y, Chen H. 2000. Rossby wave affected by large-scale topography of Qinghai-Xizang Plateau[J]. Plateau Meteor, 19(3): 331–338.
DOI:10.3321/j.issn:1000-0534.2000.03.008 |
|
刘式适, 刘式达. 2011. 大气动力学[M]. 北京: 北京大学出版社, 166-167.
Liu S S, Liu S D. 2011. Atmospheric Dynamics[M]. Beijing: Peking University Press, 166-167.
|
|
刘式适, 谭本馗. 1988. 地形作用下的非线性Rossby波[J]. 应用数学和力学, 9(3): 229–240.
Liu S S, Tan B K. 1988. Nonlinear Rossby waves forced by topography[J]. Applied Mathematics and Mechanics, 9(3): 229–240.
|
|
刘晓冉, 李国平. 2006. 青藏高原低涡研究的回顾与展望[J]. 干旱气象, 24(1): 60–66.
Liu X R, Li G P. 2006. Review and prospect of research on the Tibetan Plateau vortex[J]. Arid Meteor, 24(1): 60–66.
DOI:10.3969/j.issn.1006-7639.2006.01.013 |
|
隆霄, 程麟生. 2004. "99·6"梅雨锋暴雨低涡切变线的数值模拟和分析[J]. 大气科学, 28(3): 342–356.
Long X, Cheng L S. 2004. Numerical simulation and analysis for "99·6" Meiyu front rainstorm and the low vortex with shear line[J]. Chinese Journal of Atmospheric Sciences, 28(3): 342–356.
DOI:10.3878/j.issn.1006-9895.2004.03.03 |
|
吕克利. 1986a. 大地形对切变基流上罗斯贝波稳定性的影响[J]. 大气科学, 10(3): 327–331.
Lü K L. 1986a. The influences of large orography on instability of Rossby waves in shear currents[J]. Chinese J Atmos Sci, 10(3): 327–331.
|
|
吕克利. 1986b. 大地形和正压Rossby波的稳定性[J]. 气象学报, 44(3): 275–281.
Lv K L. 1986b. The large-scale orography and the stability of Rossby wave in the barotropic atmosphere[J]. Acta Meteor Sinica, 44(3): 275–281.
|
|
马林, 张青梅, 赵春宁, 等. 2003. 青藏高原东部牧区春季雪灾天气的形成及其预报[J]. 自然灾害学报, 12(3): 61–68.
Ma L, Zhang Q M, Zhao C N, et al. 2003. The forming and forecasting of winter snow-disaster weather in eastern pastoral-area of Qinghai-Xizang Plateau[J]. J Natural Disaster, 12(3): 61–68.
DOI:10.3969/j.issn.1004-4574.2003.03.010 |
|
乔全明, 谭海清. 1984. 夏季青藏高原500毫巴切变线的结构与大尺度环流[J]. 高原气象, 3(3): 50–57.
Qiao Q M, Tan H Q. 1984. The structure of 500mb shear line and large-scale circulation over Qingzang Plateau in summer[J]. Plateau Meteor, 3(3): 50–57.
|
|
青藏高原气象科学研究拉萨会战组. 1981. 夏半年青藏高原500毫巴低涡切变线研究[M]. 北京: 科学出版社, 120-155.
Lhasa Group of Tibetan Plateau Meteorology Research. 1981. Research of 500 mb vortex and shear lines over the Tibetan Plateau in summer[M]. Beijing: Science Press, 120-155.
|
|
师锐, 何光碧. 2011. 移出与未移出高原的高原切变线背景环流对比分析[J]. 高原气象, 30(6): 1453–1461.
Shi R, He G B. 2011. Contrast analysis on background circulation of plateau shear line moving out and not moving out of the Tibetan Plateau[J]. Plateau Meteor, 30(6): 1453–1461.
|
|
屠妮妮, 何光碧. 2010. 两次高原切变线诱发低涡活动的个例分析[J]. 高原气象, 29(1): 90–98.
Tu N N, He G B. 2010. Case analysis on two low vortexes induced by Tibetan Plateau shear line[J]. Plateau Meteor, 29(1): 90–98.
|
|
王中, 陈艳英. 2007. 触发重庆山洪灾害的典型环流和影响系统分析[J]. 高原气象, 26(3): 609–614.
Wang Z, Chen Y Y. 2007. Analyses on major effect systems and typical atmospheric circulation triggering mountain torrential disasters in Chongqing[J]. Plateau Meteor, 26(3): 609–614.
DOI:10.3321/j.issn:1000-0534.2007.03.024 |
|
伍荣生. 1964. 大地形与扰动的不稳定[J]. 气象学报, 34(1): 11–19.
Wu R S. 1964. On the influences of mountain range on the instability of disturbances[J]. Acta Meteorologica Sinica, 34(1): 11–19.
|
|
伍荣生. 1982. 基本气流和大地形对于正压波动的作用[J]. 气象学报, 40(2): 129–138.
Wu R S. 1982. The effects of basic flow and topography on the barotropic disturbances[J]. Acta Meteor Sinica, 40(2): 129–138.
|
|
谢义炳, 黄寅亮. 1964. 赤道辐合带上扰动不稳定性的简单理论分析[J]. 气象学报, 34(2): 198–210.
Xie Y B, Huang Y L. 1964. A preliminary theoretical study about the instability of the waves along the intertropical convergence zone[J]. Acta Meteor Sinica, 34(2): 198–210.
|
|
姚秀萍, 孙建元, 康岚, 等. 2014. 高原切变线研究的若干进展[J]. 高原气象, 33(1): 294–300.
Yao X P, Sun J Y, Kang L, et al. 2014. Advances on research of shear convergence line over Qinghai-Xizang Plateau[J]. Plateau Meteor, 33(1): 294–300.
DOI:10.7522/j.issn.1000-0534.2013.00164 |
|
于杰, 张继权, 朱娟, 等. 2017. 正压大气动能梯度与地转偏差的关系及其对暴雨的诊断[J]. 气象科学, 37(2): 265–271.
Yu J, Zhang J Q, Zhu J, et al. 2017. Relation between kinetic energy gradient and geostrophic deviation in barotropic atmosphere and diagnosis of torrential rain[J]. J Meteor Sci, 37(2): 265–271.
|
|
郁淑华, 高文良, 彭俊. 2013. 近13年青藏高原切变线活动及其对中国降水影响的若干统计[J]. 高原气象, 32(6): 1527–1537.
Yu S H, Gao W L, Peng J. 2013. Statistical analysis of shearline activity in QXP and its influence on rainfall in China in recent 13 years[J]. Plateau Meteor, 32(6): 1527–1537.
DOI:10.7522/j.issn.1000-0534.2012.00149 |
2. Collaborative Innovation Center on Forecast and Evaluation of Meteorological Disasters, Nanjing 210044, Jiangsu, China
 2018, Vol. 37
2018, Vol. 37
