湖陆风是一种存在明显日变化的中尺度天气现象。博斯腾湖位于中天山南麓, 湖风与天山谷风的共同存在, 使得博斯腾湖的湖风特征不同于其他湖泊。探究天山大地形对博斯腾湖湖陆风的影响, 对揭示局地环流的物理规律具有理论意义, 有助于中小尺度天气分析和预报, 同时对认识局地气候特征也是重要的。
当湖风(海风)存在时, 陆地上受热更多的空气与从湖面(海面)吹来的相对冷而薄的气层之间的交界面, 被称为湖风锋(海风锋)。Mahrer et al(1977)和Laird et al(2001)通过观测揭示了海风锋与湖风锋的明显特征, 如风速和湿度突然增加、温度降低。Sills et al(2011)观测发现, 安大略西南部、密歇根东南部和俄亥俄北部都受到了湖陆风环流的影响, 湖风锋穿透内陆距离的中值分别为75, 45和50 km。Zumpfe et al(2007)对大盐湖湖陆风进行个例分析发现, 谷风在湖风锋到达前便已开始发展, 湖风锋以大约3 m·s-1的速度沿不断抬升的地形向前推进, 在3~4 km的范围内表现为近地面风速和露点温度的快速增大。
对海陆风与邻近地形的关系的研究成果比湖陆风更为丰富, 包括地形通过自身的加热和冷却作用驱动斜坡流与海陆风结合, 从而使海陆风增强; 而地形的阻挡作用又能阻碍海风向内陆延伸。其中地形坡度、坡长、高度、山体相对于海岸线的位置以及大气热力稳定度都能影响海风的发展。Porson et al(2007)通过改变大气稳定度、坡度和坡长研究了地形对海风的影响, 发现海风的水平和垂直延展性高度依赖于地形的坡度和大气稳定性。Asai et al(1978)发现对于坡度小于2.29°的加热斜坡来说, 热力驱动产生的斜坡流能与海风耦合, Mahrer et al(1977)和Estoque et al(1981)研究发现斜坡流与海风的耦合能使海风的水平速度分量(u), 垂直速度分量(w), 水平延展性(l)和垂直延展性(h)增大, 而Porson et al(2007)研究发现, 坡度约0.8°的加热斜坡便能造成斜坡流与海风的耦合, 促进海风的发展。Ookouchi et al(1978)和Kikuchi et al(2007)发现海风与斜坡流的耦合作用能够使海风锋提前通过。Asai et al(1978)和Porson et al(2007)指出, 如果山体坡度足够陡峭的话, 海风锋向内陆的延伸将会被阻挡, 海风的u、w、l和h都会减小。阻碍斜坡流和海风耦合的临界坡度值决定于植被类型、坡长、山体与海岸线之间的距离、地形高度。Asai et al(1978)通过数值试验讨论了地形对海风的影响, 揭示了沿坡面的位温梯度决定了海陆风的发展是被增强还是被抑制。
中国具有地形复杂多样的特征, 湖泊与山体相邻较为普遍。吕雅琼等(2008)通过MM5模式模拟了纳木错湖与念青唐古拉山对局地天气的共同作用, 发现白天湖风与谷风在山脊处汇合, 形成强水平切变及辐合上升运动, 造成该地夏季白天复杂多变的天气; 夜间由于湖风与山风叠加, 为该区域补充了水汽和热量, 为白天不稳定运动提供了能量。徐安伦等(2010)利用WRF模式研究洱海湖滨大气边界层结构时发现, 在2400 m以下, 大气流场主要受苍山和洱海的影响, 存在山谷风和湖陆风两者叠加效应引起的局地环流。杨罡等(2011)利用MM5模式和卫星资料研究了鄱阳湖流域的湖陆风现象, 发现由于庐山的存在以及水域本身的走势形成的狭管效应, 使鄱阳湖中段西侧和北侧的风速明显加大。
综上所述, 不同地形分布直接影响水陆交界区域附近的局地环流发展, 博斯腾湖位于中天山南麓, 尚未见该特殊地理条件下的湖陆风特征及天山地形影响湖陆风发展的研究。为此, 本文利用基本气象站和区域气象站观测资料分析了博斯腾湖的湖陆风日变化特征和季节特征, 进而通过中尺度数值模拟分析博斯腾湖湖陆风的发展过程, 探究博斯腾湖湖陆风与天山山谷风的耦合机制。
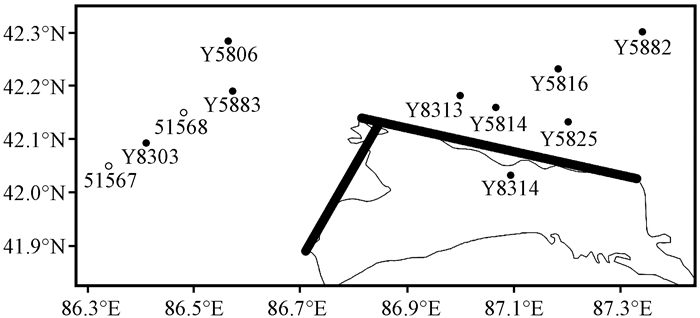
2 资料概况采用2013年6月1日至2014年5月31日巴音郭楞蒙古自治州167个站点的基本气象站和区域气象站观测资料。质量控制包括气候学界限值检查(去除0个站点)、气候学极值检查(去除10个站点)、合理性检查(去除18个站点)、内部一致性检查(去除0个站点)、时间一致性检查(去除0个站点), 缺测检查(去除99个站点), 得到有40个站点的10 m风场资料。这些站点主要分布在博斯腾湖的西北岸、西南岸和北岸。考虑湖陆风可能的影响范围, 选取离湖岸线40 km内的所有站点的风速风向资料, 其中包含湖北侧6个站, 湖西北侧5个站(图 1)。
|
图 1 站点分布湖北岸和西北岸的简化湖岸线(粗实线) ○表示基本气象站; ●为区域气象站 Fig. 1 Station locations and the roughly trend of the north and northwest shore (heavy solid line) of the Bosten Lake. ○ denote National ordinary station; ● denote regional station |
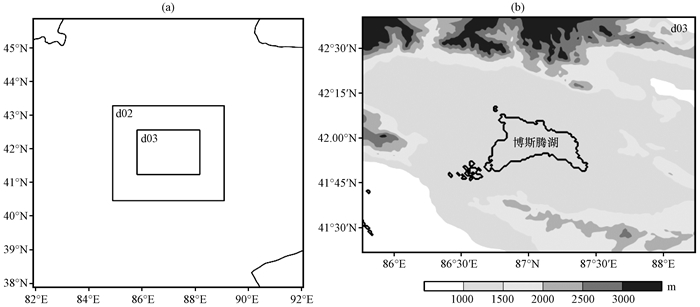
采用WRFV3.7.1模式研究博斯腾湖的湖陆风过程, 并采用NCEP 6 h一次的1°×1° FNL资料作为模式的初始场资料, 模拟时间范围为2013年7月10日06:00(当地时, 下同)至21日06:00, 2013年10月10日00:00至21日00:00, 2014年1月10日00:00至21日00:00, 2014年4月10日00:00至21日00:00, 分别代表夏、秋、冬、春四季。模拟区域以(42°N, 87°E)为中心, 三层嵌套区域的分辨率依次为9 km×9 km、3 km×3 km和1 km×1 km[图 2(a)]。水平格点数分别为100×100、124×106和208×148, 垂直方向上分为27层。
|
图 2 模拟范围(a)与内层区域地形(b, 阴影区, 单位: m) Fig. 2 The simulation area (a) and inner domain with topography (b, the shaded, unit: m) |
模式物理方案分别釆用Dudhia短波辐射方案、RRTM长波辐射方案、Lin微物理参数化方案、MYJ Monin-Obukhov近地面方案和Noah陆面过程方案。其中边界层方案采用Eta Mellor-Yamada-Janjic TKE(湍流动能)方案, 由于模拟网格距小于9 km, 且模拟期间以晴朗少云天气为主, 故不采用积云对流参数化方案。地形和土地利用类型的数据来源于NCEP提供的全球地形资料, 湖北侧山地要比湖南侧高约1 km。
4 湖陆风特征及数值模拟分析 4.1 湖陆风日变化特征湖陆风是两类下垫面受太阳辐射日变化影响作用产生的局地热力动力现象, 因此讨论博斯腾湖湖陆风季节特征时采用天文学分季方法:春季(3月17日至6月15日), 夏季(6月16日至9月24日), 秋季(9月25日至12月16日), 冬季(12月17日至次年3月16日)。
以湖北侧为例, 首先求出湖岸线(见图 1)正交方向上的站点风速分量v′, v′正值表示离岸方向, v′负值表示向岸方向。再按季节计算出湖北岸6个站v′的逐时平均值v′ja, 将四个季节的v′ja进行平均, 得到年平均日变化
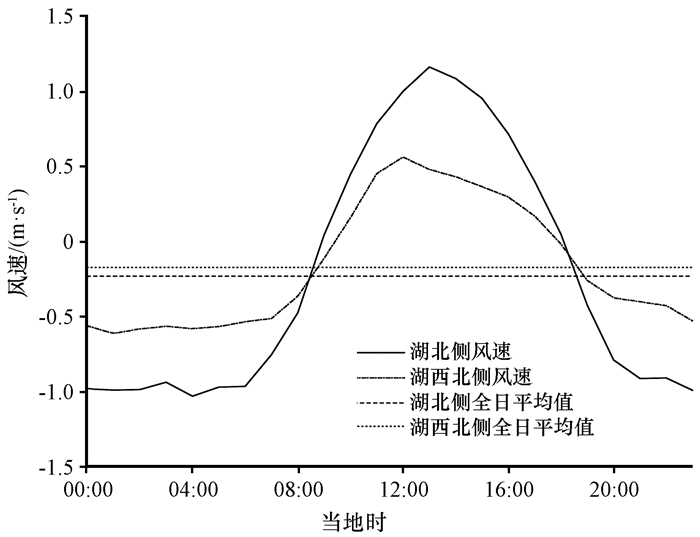
图 3表示的是湖北侧和西北侧站点在垂直湖岸方向上逐时年平均风速日变化, 对于湖北侧的站点来说, 在09:00—18:00期间
|
图 3 湖北侧和湖西北侧站点在垂直湖岸方向上逐时年平均风速日变化 Fig. 3 Station averaged hourly wind speed in the normal direction of the shore on the north and northwest to the lake |
对于湖西北侧的站点来说, 在09:00—18:00
通过比较湖北侧站点和湖西北侧站点湖陆风的日变化可以得出: (1)湖北侧站点的湖陆风比西北侧站点的更明显, 这是因为湖的北侧更加靠近北部山区, 受天山主体影响更大, 湖北侧天山谷风(简称谷风)与博斯腾湖湖风(简称湖风)叠加效应更强, 使湖北侧局地环流比湖西北侧强。此外, 凹的湖岸线会削弱湖陆风循环(McPherson, 1970; Arritt, 1989; Gilliam et al, 2004), 湖西北侧的湖岸线是凹性的, 这也使得湖西北侧的湖风风速比湖北侧站点的风速要小。(2)湖北侧站点观察到湖风开始的时间比湖西北侧站点早, 这是由于湖北侧的站点在地理位置上更接近于湖体, 而距离湖岸越近, 就会越早观察到陆风向湖风的转变。通过对比湖北侧两个与湖岸距离不同的站点(Y5814站和Y5816站)的逐时风日变化也可以证明站点距离湖体和山体远近对湖风的影响。
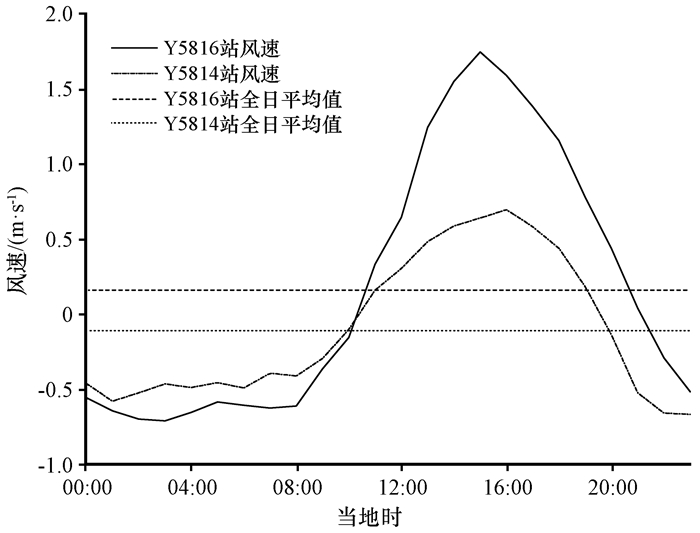
Y5816站所在位置为87.18°E, 42.23°N, 与湖岸垂直距离约为20.28 km, 与天山距离约为10.76 km, 离山近离湖远; Y5814站所在位置为87.06°E, 42.16°N, 与湖岸垂直距离约为10.9 km, 与天山距离约为21.04 km, 离山远离湖近。图 4表示的是Y5814站和Y5816站在垂直湖岸方向上逐时年平均风速日变化, 由于Y5814站离湖更近, 观测到湖风的时间比Y5816站早。Y5816站的湖风和陆风最大振幅都要大于Y5814站, 这是因为Y5816站距离湖北侧的山体比Y5814站近, 谷风与湖风的耦合作用更强。因此, 湖北侧湖陆风现象比西北侧更加明显, 并且湖北侧湖风现象出现得更早。
|
图 4 Y5814站和Y5816站逐时年平均风速日变化 Fig. 4 The hourly wind speed on Y5814 and Y5816 |
以上分析了湖陆风的日变化规律, 通过观察求得的v′ja相对于全日平均值v′a的变化情况以分析湖陆风的变化情况。当v′ja>v′a时, 认为该季节吹湖风; 当v′ja<v′a时, 认为该季节吹陆风, 用同样的方法研究湖西北岸的湖陆风季节特征。
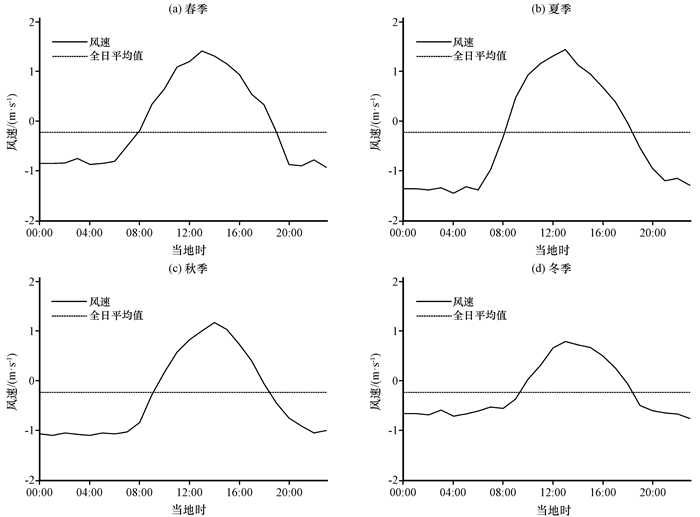
图 5为湖北侧站点四季v′ja日变化, 春季、夏季以及冬季13:00湖风强度达到最大, 而秋季14:00湖风强度达到最大, 秋季湖风风速极大值出现比其他季节晚1 h左右。夏季湖风风速极大值为1.44 m·s-1, 为全年最大, 其次为春季, 湖风风速极大值为1.41 m·s-1, 与夏季相差不大, 秋季湖风风速极大值为1.18 m·s-1, 比春、夏两季小0.23 m·s-1左右, 冬季湖风风速极大值为全年最小, 为0.8 m·s-1, 比春、夏两季小0.6 m·s-1左右。春季陆风转湖风时间为07:00—08:00, 湖风转陆风时间为19:00—20:00, 湖风持续时间为11~13 h, 为全年最长; 夏季湖风开始时间比春季推迟1 h, 湖风结束时间比春季提前1 h, 湖风持续时间比春季短2 h左右; 秋、冬两季湖风开始时间和结束时间一致, 湖风开始时间比春季推迟2 h, 湖风结束时间比春季提前1 h, 湖风持续时间比春季短3 h左右。湖风平均风速大小由强至弱排序依次为夏季、春季、秋季和冬季, 与湖风风速极大值从大到小的季节排序一致。
|
图 5 湖北侧站点在垂直湖北岸方向上各季节的逐时风速变化 Fig. 5 Station averaged hourly wind speed in the normal direction of the shore on the north to the Lake |
夏、秋两季04:00陆风强度达到最大, 而春、冬两季23:00陆风强度达到最大。夏季陆风风速极大值为1.45 m·s-1, 为全年最大, 其次为秋季, 陆风风速极大值为1.09 m·s-1, 冬季陆风风速极大值为全年最小, 为0.75 m·s-1, 比春季小0.7 m·s-1左右。陆风平均风速大小由强至弱排序依次为:夏季、秋季、春季、冬季, 与陆风风速极大值从大到小的季节排序一致。
综上, 夏季的湖风和陆风强度最大, 冬季的湖风和陆风强度最弱。春季的湖风和陆风持续时间几乎相同, 其他季节的陆风持续时间比湖风更长。
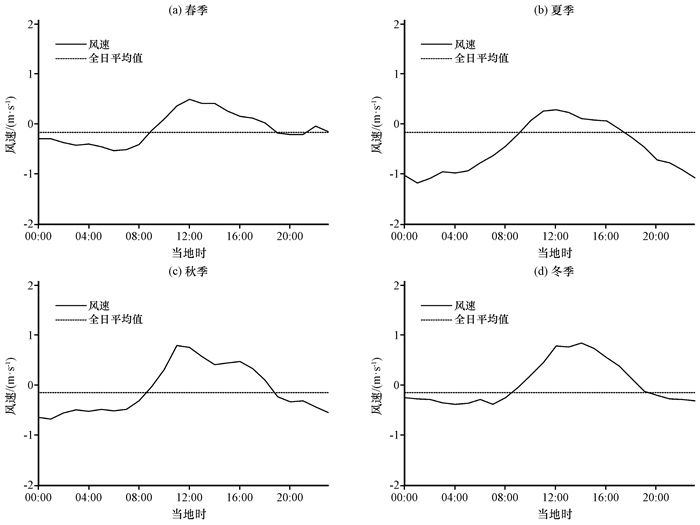
图 6为湖西北侧站点四季v′ja日变化, 春季、夏季12:00湖风强度达到最大, 而秋季11:00湖风强度达到最大, 冬季14:00湖风强度达到最大, 冬季湖风风速极大值出现比其他季节晚2~3 h。冬季湖风风速极大值为0.82 m·s-1, 为全年最大, 其次为秋季, 湖风风速极大值为0.77 m·s-1, 春季湖风风速极大值为0.49 m·s-1, 比秋、冬两季小0.3 m·s-1左右, 夏季湖风风速极大值为全年最小, 为0.28 m·s-1, 比秋、冬两季小0.5 m·s-1左右。冬季陆风转湖风时间为08:00—09:00, 湖风转陆风时间为19:00—20:00, 湖风持续时间为10~12 h, 为全年最长; 春、秋两季湖风开始时间和结束时间一致, 湖风开始时间与冬季一致, 湖风结束时间比冬季提前1 h, 湖风持续时间比春季短1 h左右; 夏季湖风开始时间比其他三季推迟1 h, 且湖风结束时间在一年中最早, 比冬季提前2 h, 湖风持续时间在一年中最短, 7~9 h。秋、冬两季湖风平均风速大小相差不大, 冬季稍大为0.52 m·s-1, 秋季为0.44 m·s-1, 春、夏两季湖风平均风速相对较小, 春季稍大为0.26 m·s-1, 夏季只有0.16 m·s-1。
|
图 6 湖西北侧站点在垂直湖西北岸方向上各季节的逐时风速变化 Fig. 6 Station averaged hourly wind speed in the normal direction of the shore on the northwest to the Lake |
夏、秋两季01:00陆风强度达到最大, 而冬季04:00陆风强度达到最大, 春季06:00陆风强度达到最大。夏季陆风风速极大值为1.17 m·s-1, 为全年最大, 其次为秋季, 陆风风速极大值为0.69 m·s-1, 冬季陆风风速极大值为全年最小, 为0.4 m·s-1, 比夏季小0.7 m·s-1左右。陆风平均风速大小由强至弱排序依次为夏季、秋季、春季和冬季, 与陆风风速极大值从大到小的季节排序相一致。
综上, 夏季和冬季刚好相反, 夏季陆风强度大而湖风强度弱, 冬季湖风强度大而陆风强度弱。各季节陆风持续时间均比湖风持续时间长。湖西北侧的湖风季节特征与湖北侧差异很大, 但陆风季节特征与湖北侧一致。
博斯腾湖夏季湖北侧湖风风速最大值为1.44 m·s-1, 在曹渐华等(2015)的研究中鄱阳湖夏季湖风最大振幅为1.2 m·s-1, 博斯腾湖湖风强度比鄱阳湖大, 这是由于在湖北侧天山大地形影响下, 谷风与博斯腾湖的湖风相互叠加, 加强了湖风的发展。此外, 这种叠加效应还使博斯腾湖湖风持续时间变长, 博斯腾湖夏季湖北侧湖风持续时间为10~12 h, 湖西北侧湖风持续时间为8~10 h, 与博斯腾湖纬度相近但周围地势平坦的密歇根湖的湖风持续时间约为9 h, 博斯腾湖北侧湖风持续时间比西北侧长2 h, 比密歇根湖长1~3 h。
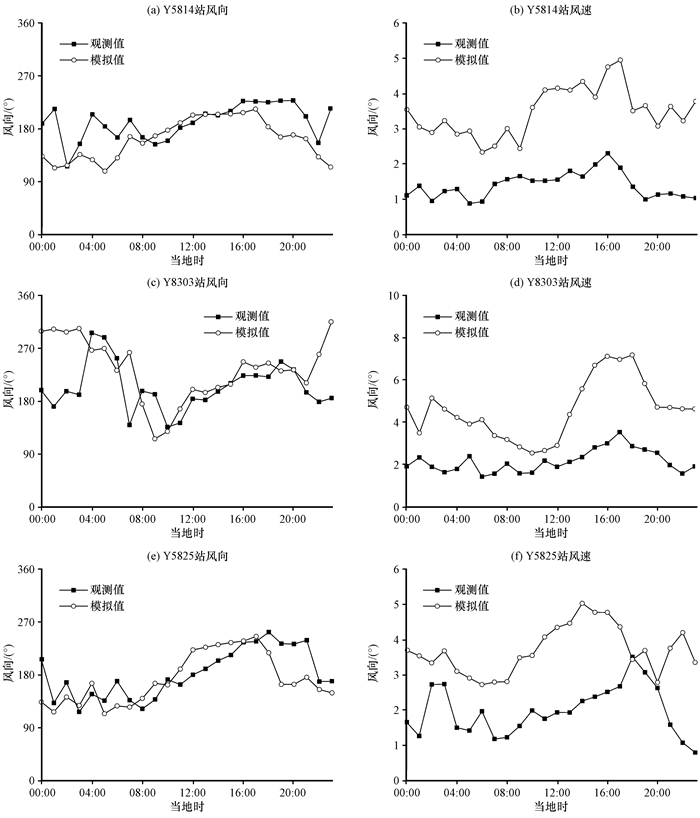
4.3 数值模拟与观测资料对比检验为了考察模拟结果的可靠性, 对2013年7月Y5814、Y8303和Y5825 3个站点的风向风速日变化的观测值与模拟值进行对比, 如图 7所示。图 7(a)、(c)、(e)中3个站点的风向模拟值与观测值曲线基本一致。
|
图 7 Y5814站、Y8303站和Y5825站的风向日变化与模拟结果(a, c, e)以及风速日变化与模拟结果(b, d, f) Fig. 7 Observation and simulation of the wind direction in Y5814, Y8303 and Y5825 (a, c, e) and wind speed in Y5814, Y8303 and Y5825 (b, d, f) |
从图 7(b), (d), (f)给出的风速看, 虽然模拟值与观测值的曲线走势较为一致, 风速最小值与最大值出现的时间点也基本吻合, 但风速模拟值相对观测值偏大, Y5814、Y8303和Y5825别偏大2, 2.4和1.7 m·s-1, 风速模拟准确性低于风向。
Shimada et al (2011)利用WRF模式中7种边界层方案进行为期一个月的风速模拟, 发现所有方案模拟的边界层低层风速均偏大。马晨晨等(2016)研究发现在复杂地形区, WRF模拟风速与观测风速之间的均方根误差比相对平坦区域更大。杨罡等(2011)模拟研究鄱阳湖边界层时也发现复杂地形环境下, 风场同样表现为较低的的模拟质量。可见复杂地形下高分辨模式性能尚有待提高。
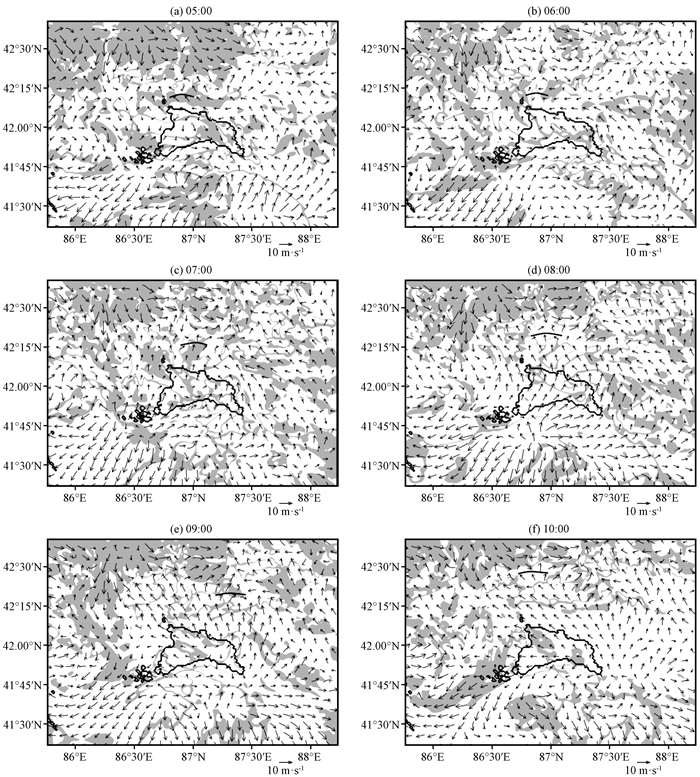
4.4 不同位置湖风的差别在湖陆风季节特征的分析中通过对比与博斯腾湖距离不同的Y5814和Y5816两个站点的日变化发现离湖越近, 湖风开始时间越早, 离山越近, 湖风的最大振幅越大。为了量化不同位置湖风的差异, 选取模拟结果中湖风过程最为明显的一次个例, 个例时间为2013年7月20日05:00—10:00, 诊断湖风锋通过的标准为:风从湖面吹向陆面且逐时露点温度差为0~ 1 ℃。图 8为7月20日05:00—10:00的10 m高度处的风场, 其中实线代表湖风锋位置。由图 8中6个时刻湖风锋位置的变化, 求得湖风锋中心经度的平均值为86.97°E, 将2013年7月11日06:00至21日06:00期间, 86.97°E, 42.15°N—42.45°N范围内的10 m高度处的风(已减去区域平均)分解到与湖北侧湖岸线(见图 1)正交方向上(v′m), 对比9个与湖岸距离逐渐变大的格点距平风vm随时间的变化, vm正值表示风由湖面吹向陆面, 各点的经纬度、与博斯腾湖和天山的距离如表 1所示。
|
图 8 2013年7月20日05:00—10:00的10 m高度风场模拟(矢量, 单位: m·s-1) 阴影表示每小时露点温度差为0~1 ℃, 黑色实线为湖风锋位置 Fig. 8 The simulated 10 m wind field (vector, unit: m·s-1) from 05:00 to 10:00 on 20 July 2013.The shaded denote dew point temperature difference per hour from 0 to 1 ℃, the black solid line denote the location of Lake Breeze front |
| 表 1 选点的经纬度、与博斯腾湖和与天山的距离及湖风最大振幅变化规律 Table 1 The latitude and longitude, the distance to the Bosten Lake and the distance to the Tianshan Mountain of selected locations and the variation of the maximum of the lake breeze |
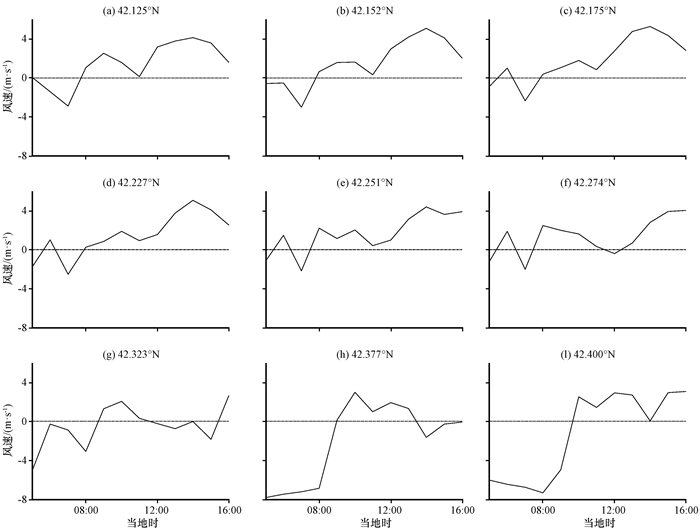
图 9表示9个格点距平风随时间的变化情况, 按格点与湖岸距离从近到远排序。结合表 1和图 9可知, 当格点与湖岸距离小于等于8.6 km时, 湖风的最大振幅随距离增大而逐渐增大。当格点纬度为42.125°N时, 湖风的最大振幅为4.15 m·s-1, 当格点纬度为42.152°N时, 湖风的最大振幅为5.11 m·s-1, 当格点纬度为42.175°N时, 湖风的最大振幅为5.28 m·s-1, 当格点纬度变化范围为42.125°N—42.175°N时, 与博斯腾湖距离每增加1 km时, 湖风的最大振幅增加约0.2 m·s-1。格点风速会同时受到天山和博斯腾湖的影响, 当与湖岸距离较小时, 在湖陆温差的影响下, 格点湖风强度很大; 随着格点与湖岸距离增大, 博斯腾湖对格点风速的影响逐渐变小, 对格点风速会有一个减小效应, 而天山谷风对格点风速的影响逐渐变大, 对格点风速会有一个增大效应, 在此范围内天山对格点风速的增大效应要比博斯腾湖对格点风速的减弱效应更大, 格点风速随与湖岸距离增大而增加。由于这三个格点与天山距离大于20 km, 受谷风影响并没有很大, 虽然格点风速逐渐增加, 但增加的幅度并不大。
|
图 9 选点逐时距平风随时间变化 Fig. 9 The hourly wind speed anomaly of the selected locations |
当格点与湖岸距离大于8.6 km且小于25 km时, 湖风的最大振幅随距离增大而逐渐减小。当格点纬度为42.227°N时, 湖风的最大振幅为5.06 m·s-1, 当格点纬度为42.251°N时, 湖风的最大振幅为4.39 m·s-1, 当格点纬度为42.274°N时, 湖风的最大振幅为4.05 m·s-1, 当格点纬度变化范围为42.227°N—42.251°N时, 与湖岸距离每增加1 km时, 湖风的最大振幅减少约0.25 m·s-1; 当格点纬度变化范围为42.251°N—42.274°N时, 与博斯腾湖距离每增加1 km时, 湖风的最大振幅只减少0.13 m·s-1。这是因为随着与湖岸距离增大, 博斯腾湖对格点风速的影响变小, 格点风速逐渐减小, 但与此同时随着与天山距离变小, 谷风对格点风速的影响在逐渐增大, 削弱了由于离湖距离变远造成的格点风速减弱效应, 所以格点风速随距离减小的幅度逐渐变小。
从与天山距离为6.12 km且与博斯腾湖距离为25 km开始, 博斯腾湖对于湖风风速的影响很小, 造成湖风风速减弱的程度也变小。天山坡面产生的谷风虽然对湖风风速有加强作用, 但是由于天山大地形对于湖风发展也有一定的机械阻挡作用, 因此虽然湖风风速受到山脚处大强度谷风的影响而增大, 但是湖风风速增大的幅度却很小。从接近天山到移动至天山脚下时(格点纬度变化范围为42.323°N—42.377°N), 与天山距离每减少1 km时, 湖风的最大振幅增加0.06 m·s-1; 当格点从天山脚下沿坡面向上移动时(格点纬度变化范围为42.377°N—42.4°N), 天山对湖风的促进作用逐渐减小, 湖风的最大振幅增加的幅度慢慢减小, 与天山脚下每增加1 km时, 湖风的最大振幅只增加0.03 m·s-1。
当格点与湖岸距离小于等于8.6 km时, 湖风开始时间规律性不强; 当格点与湖岸距离大于8.6 km且小于等于17.03 km时, 湖风开始时间都在06:00, 且湖风开始时间不随与湖距离发生变化; 当格点距离大于17.03 km时, 与博斯腾湖距离越远, 湖风开始时间越晚, 与湖距离每增加约6 km, 湖风开始时间延迟1 h。
4.5 湖风锋穿透距离除了通过垂直湖岸的逐时风的变化情况来分析湖陆风过程, 还可以通过湖风的瞬时变化来分析湖风发展情况, 主要通过分析湖风锋向内陆的渗透和湖风垂直发展的厚度。针对湖北岸和湖南岸的湖风发展情况, 在数值模拟结果中选取湖风过程最为明显的两次个例, 个例时间分别为2013年7月20日05:00—10:00和2013年7月11日08:00—13:00。
将湖风锋延伸至内陆最远处时与湖岸线的最小直线距离称之为湖风锋穿透内陆距离, 用来研究湖风的影响范围。图 8、10分别为7月20日05:00—10:00和7月11日08:00—13:00的10 m高度处风场(已减去区域平均), 阴影填色部分代表每小时的露点温度差为0~1 ℃, 实线代表湖风锋位置。通过对模拟结果的分析, 发现湖北侧和湖南侧湖风锋穿透内陆距离最远分别为39和18 km, 分别出现在7月20日10:00和7月11日13:00。湖北侧湖风锋穿透内陆距离比湖南侧大11 km, 这是因为湖北侧天山地势比湖南侧高约1 km, 湖北侧谷风强度更大且谷风与湖风的耦合作用更强, 使得湖北侧局地环流更强, 所以湖北侧湖风锋向内陆渗透作用也更强。此外, 湖北侧和湖南侧首次观测到湖风锋的时间分别为05:00和08:00, 湖北侧湖风开始时间比湖南侧提前约3 h, 说明湖北侧湖风与谷风更强的耦合作用能够使湖风锋提前通过。

|
图 10 2013年7月11日08:00—13:00的10m高度风场模拟(矢量, 单位: m·s-1) 阴影表示每小时露点温度差为0~1 ℃, 黑色实线为湖风锋位置 Fig. 10 The simulated 10 m wind field (vector, unit: m·s-1) from 08:00 to 13:00 on 11 July 2013.The shaded denote dew point temperature difference per hour from 0 to 1 ℃, the black solid line denote the location of Lake Breeze front |
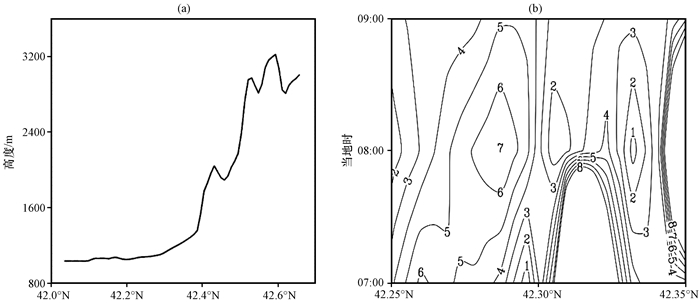
图 11(a)为86.97°E, 42°N—42.7°N剖面地形高度。在湖北侧的湖风个例中, 湖风锋在2013年7月20日07:00—09:00期间自南向北移动, 先经过平地再到达山坡, 其中07:00—08:00期间湖风锋在42.25°N—42.3°N(平地)范围内移动, 08:00—09:00期间湖风锋在42.3°N—42.35°N(坡地)范围内移动, 湖风锋移动的中心经度约为86.97°E。为了更直观地观察湖风锋从湖岸向天山移动时, 谷风与湖风耦合作用的变化规律, 图 11(b)给出了该剖面850 hPa高度处07:00—09:00风速随时间的变化, 可见随着湖风锋向天山靠近风速不断增大, 说明在湖风锋从平面移至坡面的过程中, 湖风与谷风耦合作用是不断加强的。
|
图 11 86.97°E, 42°N—42.7°N地形高度(a)和2013年7月20日07:00—09:00该剖面850 hPa高度处风速随时间的变化(b, 单位: m·s-1) Fig. 11 The terrain height (a, 11 86.97°E, 42°N—42.7°N) and the variation of wind speed in the cross section at 850 hPa from 07:00 to 09:00 on 20 July 2013 (b, unit: m·s-1) |
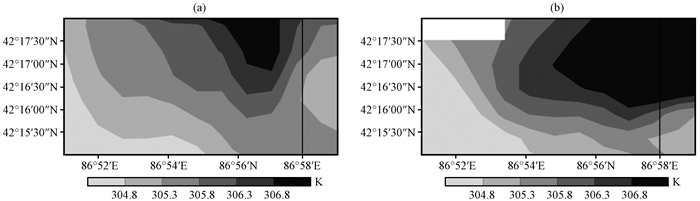
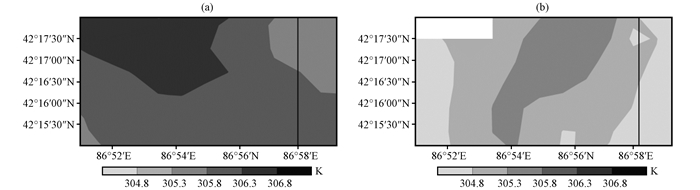
图 12和图 13分别对比了07:00和08:00时42.25°N—42.3°N(平地)和42.3°N—42.35°N(坡地)位温分布情况(在图 12和图 13中用黑色实线标出86.97°E位置), 这两个时刻坡面的水平位温梯度均与平面一致, 造成此期间低层大气产生有效位能的效率升高, 有效位能转化为大气动能的效率也升高(Asai et al, 1978), 从而促进大气运动, 因此在湖风锋从平面移至坡面的过程中, 湖风与谷风的耦合作用不断加强。
|
图 12 2013年7月20日07:00 42.25°N—42.3°N(平地)位温分布(a)和42.3°N—42.35°N(坡地)位温分布(b)(单位: K) 实线为86.97°E位置 Fig. 12 The distribution of potential temperature at plain (a) and slope (b) at 07:00 on 20 July 2013.Unit: K. Solid line represents the location of 86.97°E |
|
图 13 7月20日08:00 42.25°N—42.3°N(平地)位温分布(a)和42.3°N—42.35°N(坡地)位温分布(b)(单位: K) 实线表示86.97°E位置 Fig. 13 The distribution of potential temperature at plain (a) and slope (b) at 08:00 on 20 July 2013.Unit: K. The solid line represents the location of 86.97°E |
Comer et al (1993)通过观测证明安大略湖偏南侧湖风锋穿透内陆距离能达到45 km。安大略湖纬度与博斯腾湖相近, 但是湖风锋穿透距离却比博斯腾湖大6 km。这是因为湖陆风环流与水体尺度(d)有关, 安大略湖东西长约311 km, 南北长约85 km, 而博斯腾湖东西长55 km, 南北宽25 km, 湖风水平速度和垂直速度, 湖风锋穿透内陆距离和湖风厚度都随着d的增大而增大(Zhu et al, 2004; Neumann et al, 1975; Physick, 1976; Boybeyi et al, 1992; Segal et al, 1997), 所以安大略湖湖风锋穿透内陆距离比博斯腾湖更大。
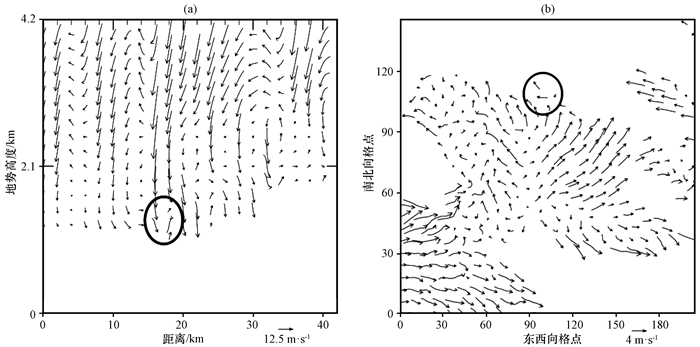
4.6 湖风厚度将观察到风向从离岸转变为向岸的点距离地面的高度, 定义为湖风的垂直厚度。为了分析湖风在垂直方向的发展, 选取湖北侧的湖风过程个例。图 14(a)为7月20日12:00 86.97°E, 42.12°N—42.50°N剖面环流, 在实线圈内风向由自南向北(湖风)转变为向上, 转变点与地面的垂直高度即为湖北侧湖风的垂直厚度, 为了判断具体高度值作出图 14(b)中7月20日12:00 1500 m处的风场图。在(86.97°E, 42.31°N)处观察到风向由离岸转变为向岸(实线圈出), 该点海拔为1163.72 m, 由此可以判断出博斯腾湖湖风厚度约为336.28 m。Laird et al (2001)研究发现密歇根湖湖风的厚度为500~750 m, 博斯腾湖湖风厚度相对于密歇根湖来说较小, 说明湖风垂直方向的发展比密歇根湖弱。湖风垂直方向发展的强弱与湖陆温差的大小有关, 夏季博斯腾湖的湖陆温差(约13 ℃)比密歇根湖湖陆温差(约16 ℃)小, 因此垂直方向发展比密歇根湖弱。
|
图 14 2013年7月20日12:00 86.97°E, 42.12°N—42.50°N剖面环流(a)和1500 m高度风场模拟(b)(单位: m·s-1) 实线圆表示风向发生转变的区域 Fig. 14 The cross section (a, 14 86.97°E, 42.12°N—42.50°N) and 1500 m wind (b) at 12:00 on 20 July 2013.Unit: m·s-1. Solid circles represent the area of the change of wind direction |
通过对博斯腾湖的湖陆风日变化特征、季节特征、发展过程及其与天山山谷风的耦合作用分析, 得出以下结论:
(1) 博斯腾湖北侧湖风与中天山南侧谷风叠加效应造成局地环流增强, 使湖北侧局地环流比湖西北侧更明显。一是因为湖北侧博斯腾湖湖风与天山谷风的耦合作用更强, 二是因为湖西北侧的湖岸线是凹性的, 对湖陆风循环有削弱作用。此外, 由于湖风与谷风的叠加效应, 与相近纬度但周围地势平坦区域的密歇根湖相比, 博斯腾湖湖北侧湖风的持续时间约长2 h。
(2) 随着与湖岸距离的增加, 湖风最大振幅存在增大、减小、再增大的现象。在湖岸附近天山对格点风速的增大效应要比博斯腾湖对格点风速的减弱效应更大, 湖风最大振幅增加; 随着与湖岸距离增大, 湖风最大振幅逐渐减小, 但与此同时随着与天山距离变小, 谷风对格点风速的影响在逐渐增大, 削弱了由于离湖距离变远造成的格点风速减弱效应, 所以湖风最大振幅随距离减小的幅度逐渐变小; 到达天山山脚时, 格点风速受到山脚处大强度谷风的影响而增大, 湖风最大振幅增大, 但是由于天山大地形对湖风发展有一定的机械阻挡作用, 湖风最大振幅增大的幅度逐渐变小。
(3) 湖风开始时间起先随距离变化不显著, 之后与博斯腾湖的距离每增加约6 km, 湖风开始时间推迟1 h。
(4) 博斯腾湖湖陆风的强度和持续时间有着季节性变化。湖北侧夏季的湖陆风强度最大, 冬季的湖陆风强度最弱, 春季的湖风和陆风持续时间几乎相同, 其他季节的陆风持续时间比湖风更长; 湖西北侧夏季和冬季刚好相反, 夏季陆风强度大而湖风强度弱, 冬季湖风强度大而陆风强度弱, 各季节陆风持续时间均比湖风持续时间长。
(5) 湖北侧天山的地势比湖南侧高约1 km, 湖北侧谷风更强且湖风与谷风耦合作用更强, 使得湖北侧湖风锋穿透内陆距离比湖南侧远约11 km。
(6) 天山地形也会促进湖风在水平和垂直方向上的发展, 随着湖风锋向天山靠近, 谷风与湖风的耦合作用不断加强。
Arritt R W. 1989. Numerical modelling of the offshore extent of sea breezes[J]. Quarterly Journal of the Royal Meteorological Society, 115(487): 547–570.
DOI:10.1002/(ISSN)1477-870X |
|
Asai T, Mitsumoto S. 1978. Effects of inclined land surface on the land and sea breeze circulation:A numerical experiment[J]. Journal of the Meteorological Society of Japan, 56(6): 559–570.
DOI:10.2151/jmsj1965.56.6_559 |
|
Boybeyi Z, Raman S. 1992. A three-dimensional numerical sensitivity study of mesoscale circulations induced by circular lakes[J]. Meteorology and Atmospheric Physics, 49(1/4): 19–41.
|
|
Comer N, Mckendry I. 1993. Observations and numerical modelling of Lake Ontario breezes[J]. Atmosphere, 31(4): 481–499.
|
|
Estoque M A, Gross J M. 1981. Further studies of a lake breeze partⅡ:theoretical study[J]. Monthly Weather Review, 109(3): 619–634.
DOI:10.1175/1520-0493(1981)109<0619:FSOALB>2.0.CO;2 |
|
Gilliam R C, Raman S, Niyogi D D S. 2004. Observational and numerical study on the influence of large-scale flow direction and coastline shape on sea-breeze evolution[J]. Boundary-Layer Meteorology, 111(2): 275–300.
DOI:10.1023/B:BOUN.0000016494.99539.5a |
|
Kikuchi Y, Arakawa S, Kimura F, et al. 1981. Numerical study on the effects of mountains on the land and sea breeze circulation in the Kanto District[J]. Journal of the Meteorological Society of Japan, 59(5): 723–738.
DOI:10.2151/jmsj1965.59.5_723 |
|
Laird N F, Kristovich D A R, Liang X Z, et al. 2001. Lake Michigan lake breezes:climatology, local forcing, and synoptic environment[J]. Journal of Applied Meteorology, 40(3): 409–424.
DOI:10.1175/1520-0450(2001)040<0409:LMLBCL>2.0.CO;2 |
|
Mahrer Y, Pielke R A. 1977. The effects of topography on sea and land breezes in a two-dimensional numerical model[J]. Monthly Weather Review, 105(9): 235–240.
|
|
Mcpherson R D. 1970. A numerical study of the effect of a coastal irregularity on the sea breeze[J]. Journal of Applied Meteorology, 9(5): 767–777.
DOI:10.1175/1520-0450(1970)009<0767:ANSOTE>2.0.CO;2 |
|
Neumann J, Mahrer Y. 1975. A theoretical study of the lake and land breezes of circular lakes[J]. Monthly Weather Review, 103(6): 474–485.
DOI:10.1175/1520-0493(1975)103<0474:ATSOTL>2.0.CO;2 |
|
Ookouchi Y, Uryu M, Sawada R. 1978. A numerical study on the effects of a mountain on the land and sea breezes[J]. Journal of the Meteorological Society of Japan, 56(3): 368–386.
|
|
Physick W L. 1976. A numerical model of the sea breeze phenomenon over a lake or gulf[J]. Journal of the Atmospheric Sciences, 33(11): 2107–2135.
DOI:10.1175/1520-0469(1976)033<2107:ANMOTS>2.0.CO;2 |
|
Porson A, Steyn D G, Schayes G. 2007. Sea breeze scaling from numerical model simulations, partⅡ:Interaction between sea breezes and slope flows[J]. Boundary-Layer Meteorology, 122(1): 31–41.
DOI:10.1007/s10546-006-9092-2 |
|
Segal M, Leuthold M, Arritt R W, et al. 1997. Small lake daytime breezes:some observational and conceptual evaluations[J]. Bulletin of the American Meteorological Society, 78(6): 1135–1147.
DOI:10.1175/1520-0477(1997)078<1135:SLDBSO>2.0.CO;2 |
|
Shimada S, Ohsawa T, Chikaoka S, et al. 2011. Accuracy of the wind speed profile in the lower PBL as simulated by the WRF model[J]. Scientific Online Letters on the Atmosphere, 7: 109–112.
|
|
Sills D M L, Brook J R, Levy I, et al. 2011. Lake breezes in the southern Great Lakes region and their influence during BAQS-Met 2007[J]. Atmospheric Chemistry and Physics, 11(15): 7955–7973.
DOI:10.5194/acp-11-7955-2011 |
|
Zhu M, Atkinson B W. 2004. Observed and modelled climatology of the land-sea breeze circulation over the Persian Gulf[J]. International Journal of Climatology, 24(7): 883–905.
DOI:10.1002/(ISSN)1097-0088 |
|
Zumpfe D E, Horel J D. 2007. Lake-breeze fronts in the Salt Lake Valley[J]. Journal of Applied Meteorology and Climatology, 46(2): 196–211.
DOI:10.1175/JAM2449.1 |
|
曹渐华, 刘熙明, 李国平, 等. 2015. 鄱阳湖地区湖陆风特征及成因分析[J]. 高原气象, 34(2): 426–435.
DOI:10.7522/j.issn.1000-0534.2013.00197 |
|
吕雅琼, 马耀明, 李茂善, 等. 2008. 纳木错湖夏季典型大气边界层特征的数值模拟[J]. 高原气象, 27(4): 733–740.
|
|
马晨晨, 余晔, 何建军, 等. 2016. 次网格地形参数化对WRF模式在复杂地形区风场模拟的影响[J]. 干旱气象, 34(1): 96–105.
|
|
徐安伦, 董保举, 刘劲松, 等. 2010. 洱海湖滨大气边界层结构及特征分析[J]. 高原气象, 29(3): 637–644.
|
|
杨罡, 刘树华, 朱蓉, 等. 2011. 鄱阳湖地区大气边界层特征的数值模拟[J]. 地球物理学报, 54(4): 896–908.
DOI:10.3969/j.issn.0001-5733.2011.04.003 |
 2019, Vol. 38
2019, Vol. 38

