2. 中国科学院大学, 北京 100049
额济纳绿洲位于黑河下游, 气候极端干旱, 沿河道分布着的以胡杨和柽柳为优势种的荒漠河岸林对于遏制沙漠化, 保障绿洲稳定具有重要的意义。维持额济纳荒漠河岸林生态系统结构稳定和正常生态功能的水分主要来源于受河道径流补给的浅层地下水(尹力等, 2012; 高冠龙等, 2017)。由于黑河中游灌溉农业的发展利用了大量的河水, 黑河下游河道干涸, 导致额济纳绿洲生态严重退化。为恢复额济纳绿洲的生态系统, 从1999年国家开始实施黑河分水计划, 每年多次向下游河道放水, 进入下游的河道径流补给河岸周边的地下水, 从而维持了一定范围的地下水位, 为河岸林系统的健康提供了重要的保障。河岸林植物通过深根系利用河岸浅层地下水维持其正常生长, 也是河岸浅层地下水的主要排泄方式, 因此, 深入了解河岸林地下水蒸散发规律对于维持适当的河岸林地下水位, 保障河岸林生态系统正常的生态功能和维持绿洲生态系统稳定具有重要的意义。
蒸散发过程是水循环中的重要环节, 主要包括土壤及水体蒸发和植物蒸腾两大部分。在干旱半干旱地区, 荒漠河岸林主要依靠浅层地下水来维持其正常生长, 其造成的地下水蒸散在蒸散发总量中占很大的比重, 而且气候越干旱, 地下水埋藏越浅, 地下水蒸散在总蒸散中所占的比重也越大(Lubczynski, 2009)。额济纳绿洲气候极度干旱, 且河岸林地下水埋深较浅, 地下水蒸散占河岸林蒸散总量的绝大部分, 所以河岸林地下水蒸散信息在很大程度上反映了蒸散总量的特征。在之前的研究中, 地下水蒸散发被认为是陆地水循环中最难获取准确数据的一个过程(Loheide et al, 2005)。目前获取蒸散数据的方法主要有蒸发皿、蒸渗仪、树干液流观测计和涡度相关通量塔等仪器直接观测(Howell et al, 1998; Swinbank, 1951; 杨光超等, 2015; 陈伯龙, 2017), 蒸散发估算经验模型(Priestley et al, 1972; Thornthwaite, 1948), 过程模型(如Penman-Monteith)(Monteith, 1965), 遥感蒸散发估算方法(如SEBAL)(Bastiaanssen et al, 1998), 同位素示踪方法(Brunel et al, 1995; Chimner et al, 2004)和水量平衡残余法(Weeks et al, 1973)等, 上述方法在进行蒸散估算时都有一定的假设和适用条件。在极端干旱的额济纳绿洲, 荒漠河岸林沿河道呈带状分布, 且随着与河道的距离增加, 河岸林的地下水位、土壤性质和植被分布等都具有显著的空间异质性, 使用上述方法进行荒漠河岸林蒸散发研究时, 具有一定的局限性, 影响所获取的蒸散数据的可靠性。而地下水位日变化方法(Gribovszki et al, 2008; Yin et al, 2013; Fan et al, 2015)可以通过获得荒漠河岸林连续的地下水日变化结果进行蒸散估算, 这是其他方法很难做到的, 另外, 地下水位日变化是其地表所有利用地下水的植被作用的总和, 而地表植被往往具有很强的异质性, 使用其他方法往往会产生较大的误差, 并且这种方法应用简单而且成本较低。应用最为广泛的利用地下水位日变化估算深根植物造成的地下水蒸散的方法是White方法(White, 1932)。
本研究主要通过分析位于极端干旱区的额济纳绿洲荒漠河岸林的蒸散消耗对于地下水位变化的影响, 评估地下水位日变化方法在额济纳绿洲荒漠河岸林进行地下水蒸散估算的适用性及估算结果的准确性, 以期为保证河岸林生态系统稳定和实现地下水的可持续利用提供科学支撑。
2 研究区概况和研究方法 2.1 研究区概况研究区地处黑河流域下游额济纳绿洲, 范围为40°57′N—42°30′N, 99°53′E—102°10′E, 海拔为900~1100 m[图 1(a)]。该地深居内陆, 气候极度干旱, 多年平均降水量为37.9 mm, 且75%以上集中在6—8月; 而年潜在蒸发量高达3700 mm以上, 约为降水量的100倍; 年均气温7月最高, 为27.0 ℃, 1月最低, 为-11.7 ℃。本区地表水资源贫乏, 地下水补给量少且水质差, 额济纳河是当地生物赖以生存的水源, 沿河分布着以胡杨和柽柳为优势树种的荒漠河岸林。在远离河道处, 植被稀疏低矮, 种类简单, 以一些旱生和超旱生的灌木和半灌木为主(龚家栋等, 1998), 天然植被正常生长所需要的水分主要依靠地下水的补给(张武文等, 2002), 而该区地下水的主要来源为上中游的下泄河水渗漏补给以及额济纳盆地周边侧渗补给。

|
图 1 研究区位置及观测点布设 Fig. 1 Location map of study area and the groundwater wells |
在额济纳旗七道桥胡杨林保护区试验点内, 布设有地下水位观测井[图 1(c)], 观测井中安装有自计水压和水温传感器(HOBO U20-001-04, Onset Computer Corporation, USA), 传感器记录间隔为10 min。此外, 还设置了一个位于井外的HOBO传感器来记录外部大气压的变化, 记录间隔也设置为10 min。用井中传感器测得的水压减去外部传感器获取的大气压, 就得到了传感器以上水柱所施加的压力, 最后, 再根据水柱对传感器施加的压力求得地下水位。
2.2.2 涡度相关观测及数据处理在阿拉善荒漠生态水文试验站七道桥胡杨林试验地布设了通量观测塔[图 1(d)], 其上安装的涡度相关观测仪器包括三维超声风速系统(CSAT3, Campbell Co, USA)和开路式CO2/H2O分析仪(Li-7500A, LI-COR, USA), 净辐射传感器(CNR4, Kipp & Zonen, Netherlands), 温度相对湿度传感器(HMP45C, Vaisala, USA), 以上所有数据通过数据采集器(CR3000)自动采集, 采样频率为10 Hz。涡度协方差原始数据采用Eddy Pro软件预处理(LI-COR, USA), 输出0.5 h平均的感热通量(H, 单位: W·m-2)和潜热通量(LE, 单位: W·m-2)作为分析数据。预处理后, 首先剔除明显错误和典型降雨日数据; 其次考虑湍流稳定性剔除摩擦风速u*<0.1 m·s-1; 缺失数据插补采用查找表法(Falge et al, 2001), 最后利用能量平衡分析, 基于波文比将多余能量分别分配给感热和潜热(Wohlfahrt et al, 2009), 获取最终的感热通量和潜热通量数据。
2.2.3 气象数据来源试验地气象资料来自于阿拉善荒漠生态水文试验站自动气象站(ENVIS), 包括气温、日照、气压、湿度和风速风向等气象要素。
2.3 试验方法(1)参考蒸散计算方法
Penman-Monteith模型是目前使用最为普遍的蒸散估算方法, 本文采用FAO推荐的Penman-Monteith方法(Allen et al, 1998)对试验点的参考蒸散发(ET0, 单位: mm·d-1)进行计算, 公式如下:
| $ E{T_0} = \frac{{0.408\mathit{\Delta }\left({{R_n} - G} \right) + \gamma \frac{{900}}{{T + 273}}{u_2}\left({{e_s} - {e_a}} \right)}}{{\mathit{\Delta } + \lambda \left({1 + 0.34{u_2}} \right)}}, $ | (1) |
式中: ET0为潜在蒸散量(单位: mm·d-1); Rn为净辐射量(单位: MJ·m-2·d-1); G为土壤热通量(单位: MJ·m-2·d-1); γ为湿度计常数[单位: kPa·(℃)-1]; γ为饱和水汽压与温度关系曲线的斜率[单位: kPa·(℃)-1]; T为空气平均温度(单位: ℃); u2为在地面以上2 m处的风速(单位: m·s-1); es为空气饱和水汽压(单位: kPa); ea为空气实际水汽压(单位: kPa)。
(2) 单作物系数法
除了水热条件的调控, 陆表蒸散发也取决于植被生理耗水和土壤水分条件(王帅兵等, 2015)。FAO推荐的单作物系数法可以较好计算包括植被蒸腾和土壤蒸发在内的陆表蒸散发过程:
| $ ET = {K_C} \times E{T_0}, $ | (2) |
式中: ET为实际蒸散发量(单位: mm·d-1); KC为单作物系数; ET0为潜在蒸散发(单位: mm·d-1)。
单作物系数综合考虑了土壤蒸发和植物蒸腾, 主要根据植物生长发育状况和土壤水含量来确定。
(3) 地下水蒸散估算方法
高频率的地下水位观测为揭示地下水位的日波动过程提供了基础。根据地下水位日波动数据, White(1932)基于水量平衡原理提出了一种估算地下水蒸散的方法(ETG), 该方法有以下几个重要的假设: ①地下水位日波动是植物耗水造成的; ②植物夜间耗水可以忽略); ③ 00:00(北京时, 下同)—04:00的地下水位回升速率可以代表全天平均地下水补给速率。使用White方法获取地下水蒸散的公式如下:
| $ E{T_G} = {S_y}\left({24r \pm s} \right), $ | (3) |
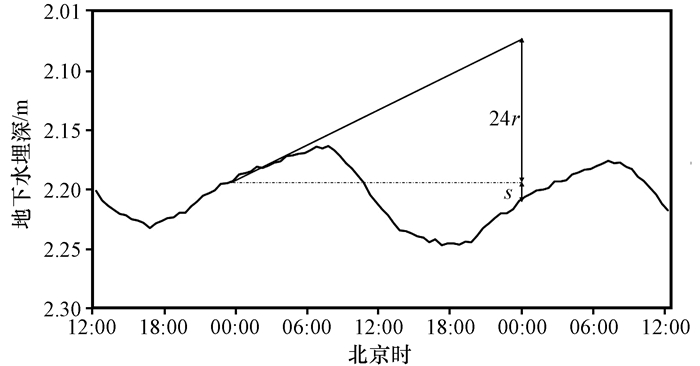
式中: ETG是日地下水蒸散量(单位: mm·d-1); Sy是给水度; r是00:00—04:00地下水位回升速率(单位: mm·h-1); s是24 h地下水位变化幅度(下降为正, 上升为负, 单位: mm·d-1)。公式中的r和s两个变量从地下水位变化曲线中获得, Sy则主要受土壤质地及水位埋深的影响(图 3)。Loheide et al(2005)在此前的研究结果表明, Sy的取值是使用White方法估算地下水蒸散误差的主要来源, 并提出了一种确定合适Sy的方法, 根据该方法, 依据对地下水位观测井附近地下水位处的土壤质地分析结果, 最终确定七道桥胡杨保护区的Sy取值为0.08。在一些研究中发现, r使用当日及后一日00:00—04:00水位变化速率的均值可以提高估算的准确性, 所以本文也将采用两日的r均值来估算日地下水蒸散量。
|
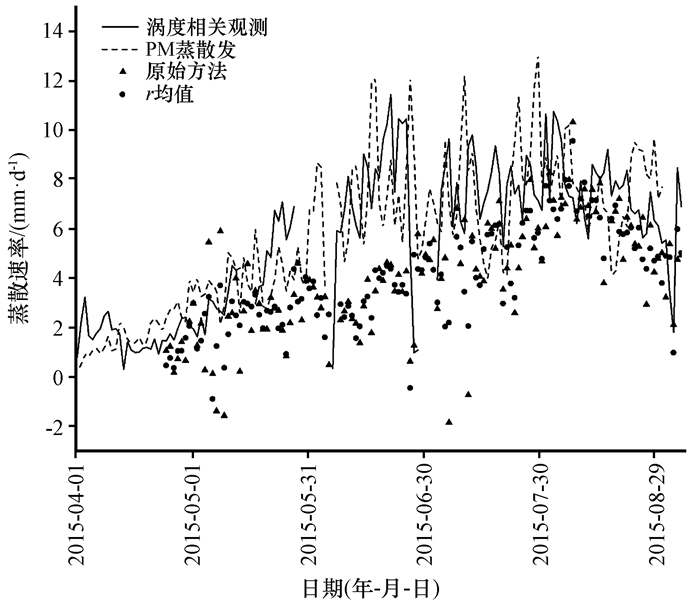
图 3 2015年七道桥胡杨林不同方法蒸散估算结果与涡度相关观测结果 Fig. 3 The estimated evapotranspiration using different methods and the observed evapotranspiration from Eddy covariance method at Qidaoqiao populous euphrarica forest in the growing season of 2015 |
首先, 利用FAO推荐的Penman-Monteith方法对额济纳绿洲2015年的参考蒸散发进行了计算。因为FAO-PM方法计算的结果是在假设植物高度为0.12 m, 并有固定的叶面阻力为70 m·s-1, 反射率为0.23, 相当于高度一致、生长旺盛、完全覆盖地面而不缺水的开阔草地的蒸散发, 主要是由气象要素, 如:热量, 辐射, 饱和蒸气压差等决定的, 而不考虑植物生长阶段和水分供应的影响, 所以计算结果表现出了同温度, 降水同步的显著的季节变化, 年最高日蒸散速率都出现在夏季, 2015年的参考蒸散量为1705 mm。
然后, 通过胡杨不同生长阶段的生理状况以及土壤含水量确定了胡杨林的单作物系数, 并根据计算得到的参考蒸散求得2015年七道桥胡杨林的蒸散量。
3.2 基于地下水位变化的蒸散估算由于植物生长季蒸腾耗水对于地下水的强烈消耗, 使得河岸林地下水位植物生长季时表现出日尺度的波动变化特征, 这个现象在之前的许多浅层地下水研究中都有发现(Dulohery et al, 2000; Dahm et al, 2002; 袁国富等, 2015)。额济纳绿洲荒漠河岸林地下水位的日尺度波动特征在4月下旬开始出现, 到9月底时消失。从七道桥胡杨林地下水观测井2015年7月25—27日48 h的地下水位变化状况(图 2)可以看出, 观测水位表现出了明显的日周期变化, 经过地下水位的高值都出现在09:00左右, 而经过日间的植物蒸腾消耗后, 在18:00左右到达日最低水位, 地下水日变化幅度方面约为0.1 m。
|
图 2 胡杨林地下水位日变化状况及White方法示意图 Fig. 2 Example of diurnal water table fluctuations observed from three monitoring wells at populous euphrarica forest from 25 to 27 July 2015, and the basic principle of the original White method |
使用White方法根据额济纳旗七道桥胡杨保护区内的地下水位观测井2015年5—8月的水位变化数据进行了地下水蒸散估算, 其中r分别采用当日和当日及后一日00:00—04:00水位变化速率的均值, Sy取0.08, 并将估算的地下水日蒸散速率与FAO-PM单作物系数方法蒸散发估算结果和涡度相关方法获得的蒸散观测值进行了比较(图 3)可以看到, 估算得到的地下水日蒸散量与观测日蒸散量具有较为一致的变化趋势, 原始方法和使用r均值的改进方法获得的结果与观测数据的相关系数分别为0.48和0.54, p均小于0.01。2015年生长季中有地下水位数据期间使用原始及改进方法得到的地下水蒸散估算值总量为517 mm和520 mm, 同期内的涡度相关方法观测蒸散总量为750 mm。
胡杨林地下水日蒸散的高值出现在7—8月, 在这两个月内胡杨林使用原始及改进方法估算的地下水日蒸散平均速率分别为5.52和5.50 mm·d-1。从7—8月的平均地下水日蒸散速率估算结果来看, 使用r均值和原始方法并没有明显的差异, 但在生长及初期和末期, 使用r均值进行估算显著地避免了估算中蒸散负值及离群值的出现。
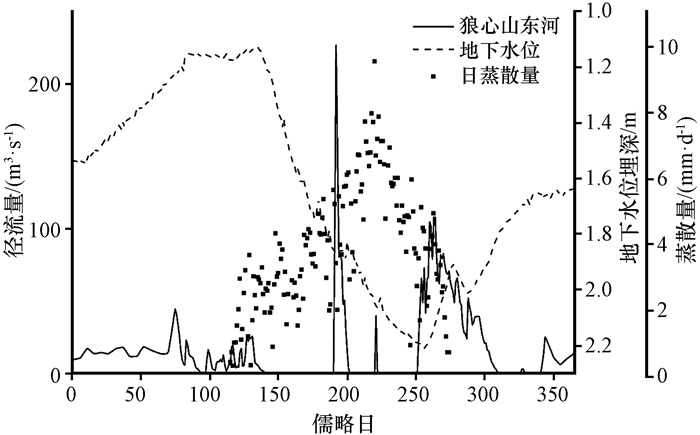
3.3 荒漠河岸林地下水位变化及其与胡杨蒸散关系分析额济纳绿洲荒漠河岸林地下水位的变化主要是由河道侧渗对地下水的补给以及河岸林植物耗水造成的。通过2015年河岸胡杨林地下水位观测井中水位的变化过程, 以及额济纳绿洲上游狼心山水文站记录的额济纳东河日径流量数据(图 4)可以看出, 2015年中观测井的地下水位在1.1~2.3 m之间变化, 黑河分水对于下游绿洲地下水位有着重要影响, 额济纳荒漠河岸林地下水位的抬升主要发生在有河水下泄的时间段。而地下水位的下降主要发生在5—10月, 即荒漠河岸林植物生长季, 额济纳荒漠河岸林的植物普遍具有较深的根系, 可以直接利用地下水或者利用地下水位上部土壤中来自地下水的水分, 因此, 在植物生长季中, 植物强烈的蒸腾作用就成了河岸林地下水重要的消耗途径。在没有河道径流补给的情况下, 植物生长季耗水可使地下水位下降1 m左右。在河道径流补给和植物耗水的共同作用下, 额济纳荒漠河岸林地下水位表现出非生长季(10月至次年4月)地下水位抬升, 而生长季(5—9月)地下水位下降, 及存在上游来水时的间歇性抬升或下降速率减缓等特点。
|
图 4 2015年东河径流与河岸林地下水位 Fig. 4 Discharge of Donghe river and the groundwater levels of desert riparian forests in 2015 |
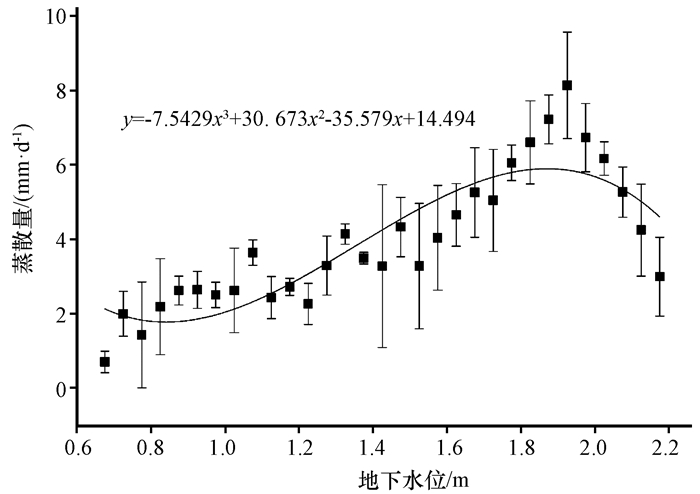
作为荒漠河岸林的主要水分来源, 河岸林地下水位与胡杨蒸散之间存在紧密的联系和相互作用, 胡杨的生长季耗水造成地下水位的持续下降, 而不同的地下水位埋深也对胡杨的蒸腾具有调节作用。图 5中描述了2015年生长季胡杨林日蒸散速率与地下水位之间的关系, 并使用三次多项式进行了拟合(R2=0.75)。从图 5中可以看到, 胡杨日蒸散速率在地下水位为1.8~2 m时达到了最高值, 而从不同地下水位时胡杨日蒸散速率的标准差来看, 地下水位为1.4~1.6 m时日蒸散速率的标准差较大, 说明当地下水埋深位于1.4~1.6 m时胡杨的日蒸散速率具有较大的差异性。
|
图 5 胡杨林蒸散量与地下水位的关系, 误差棒表示标准差 Fig. 5 Relationship between evapotranspiration rate of Populus euphratica and depth to water, vertical bars represent the standard deviations |
使用White方法估算得到的荒漠河岸林生长季地下水蒸散结果与涡度相关实测蒸散和参考蒸散在季节性变化和日际波动上都具有比较好的一致性。但是在地下水蒸散发结果中出现了一些负值, 主要是集中在生长及的初期和末期, 以及存在较显著的河水补给地下水现象时, 这是因为, 在上述情况下实际的地下水位变化状况可能并不满足White中的基本假设, 在生长季初期及末期, 由于植物蒸腾速率较低, 植物耗水在地下水消耗中所占的比例较小, 地下水位日波动中包含的植物蒸散信息被其他一些因素所干扰, 导致估算结果出现一定误差; 而存在河流对地下水的补给行为时, 由于河道径流的不稳定性, 导致地下水补给速率出现较大变化, 违背了地下水补给速率恒定这一假设, 从而对地下水蒸散产生误估。
地下水蒸散只是生态系统总蒸散量的一部分, 使用r均值方法获得的七道桥胡杨林2015年5—8月的地下水蒸散估算总量占同期涡度观测蒸散总量的70%左右。在之前Good et al(2015)的研究中发现, 植物蒸腾约占全球陆地总蒸散量的64%±13%, 而蒸发有65%±26%左右来自于土壤蒸发, 而且地下水的埋深对蒸散发总量中蒸腾和蒸发所占的比重有着重要的影响。七道桥胡杨林估算的地下水蒸散占涡度观测蒸散比例相比Good et al(2015)研究中得到的结果较高, 主要原因可能是, 由于降水稀少和强烈蒸散的自然条件, 浅层土壤极度干燥, 地下水是荒漠河岸林植物最重要的水分来源。胡杨和柽柳等耐旱植物通常具有较深的根系, 可以直接或间接使用地下水, 而这些深根树木根系的水力提升作用也为林下的草本植物提供了生存用水(Prieto et al, 2012; Barrongafford et al, 2017; 鱼腾飞等, 2017a), 所以地下水位日波动是由其地表一定范围内所有植物生存耗水造成的, 使用White方法估算得到的地下水蒸散速率也就近似等于荒漠河岸林的植物总蒸腾量加上一部分土壤蒸发, 就使得通过地下水位变化估算得到的蒸散量占观测总蒸散量的比例较高。
4.2 荒漠河岸林基于地下水位变化的蒸散发估算结果的变化特征2015年生长季胡杨林下的平均和最高地下水蒸散速率分别为3.9和9.5 mm·d-1, 最高地下水蒸散速率出现在了7月中旬。从图 5中可以看到, 地下水蒸散速率从5月初开始增加, 在7月初达到蒸散速率的高值, 并在接下来的一个多月中保持着相对的稳定, 于8月下旬开始下降。胡杨林下的地下水蒸散发估算与参考蒸散估算在7月初至8月下旬之间具有极为类似的变化特征。Butler et al(2007)此前指出, 影响地下水蒸散变化的主要因素是地表植物的叶片生长状况。额济纳胡杨展叶的时间通常在4月末到5月初, 在第一次展叶高峰期内展叶数量占整个生长季展叶总数的80%~90%以上, 随后仅在6月略有增加, 基本保持稳定, 直到9月初进入落叶期(余伟莅, 2013), 这在很大程度上决定了胡杨蒸腾速率的季节变化。由于胡杨在6月中旬时, 其叶片发育已经基本完成, 因此在之后其蒸腾速率受参考蒸散发所表征的能量限制的蒸散能力的影响更大, 所以地下水蒸散的估算值也就与参考蒸散估算具有了更相似的变化特征。
4.3 植物夜间蒸腾对基于地下水变化的蒸散估算结果的影响在White方法中的一个重要假设是植物夜间蒸腾不存在或者可以忽略, 但是在随后的很多研究中都发现了多种植物都具有显著的植物夜间蒸腾现象(Caird et al, 2007; Zeppel et al, 2013), 关于额济纳绿洲胡杨夜间蒸腾的研究也取得了一些进展(司建华等, 2014; 赵春彦等, 2015; 鱼腾飞等, 2017b)。Fan et al(2016)在之前的研究中分析了植物夜间蒸腾对于使用White方法估算地下水蒸散的影响, 结果表明在忽略植物夜间蒸腾的情况下, 在其研究时段内White方法低估了约25%。
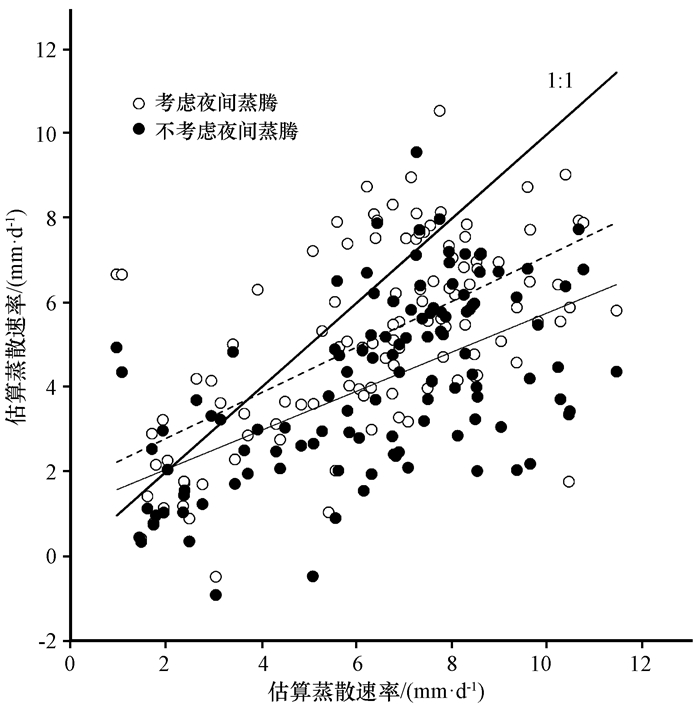
在本次研究中, 根据鱼腾飞等(2017b)对于胡杨夜间蒸腾的研究, 使用一个单峰曲线代表胡杨生长季内的夜间蒸腾平均速率变化。然后在考虑胡杨夜间蒸腾的状况下, 使用r均值方法, 对七道桥胡杨林的地下水蒸散再次进行了估算, 并与不考虑夜间蒸腾的估算结果及涡度观测蒸腾数据进行了比较。在加入夜间蒸腾之后, 研究时段内地下水蒸散估算速率与观测蒸散速率的相关性为0.61(p<0.01), 比忽略夜间蒸腾时有了显著提高, 地下水蒸散总量增加了70 mm, 地下水蒸散占涡度观测蒸散的比例提高到了90%(图 6)。
|
图 6 考虑胡杨夜间蒸腾后的蒸散估算结果与观测蒸散的比较 Fig. 6 The estimated evapotranspiration considered the nocturnal transpiration of Populus euphratica and the comparison with the observed evapotranspiration from Eddy covariance method |
河道径流和植物蒸腾是河岸林地下水变化的两个最重要影响因素, 植物的蒸腾耗水是荒漠河岸林地下水最重要的消耗方式。本文根据实测高分辨率地下水位数据进行了荒漠河岸林胡杨蒸散发估算, 并与涡度相关观测数据进行比较以验证地下水位日波动方法在额济纳绿洲荒漠河岸林生态系统的适用性。主要结论如下:
(1) 利用地下水位日波动方法(White方法)得到的七道桥胡杨林地下水蒸散量与涡度相关数据和FAO-PM蒸散估算具有较为一致的变化趋势和显著的相关关系, 说明White方法是获取荒漠河岸林地下水蒸散数据的可靠方法。
(2) 使用White方法估算得到的2015年生长季荒漠河岸胡杨林的地下水蒸散发为520 mm, 且其季节变化近似表现为单峰曲线, 在7—8月的地下水蒸散速率都保持相对稳定。
(3) 由于生长季初期和末期, 植物蒸腾较弱, 地下水位变化中所包含的植物蒸散信息也就相对较少, 所以估算结果在这一时段出现了一定的误差; 而对于植物夜间蒸腾的忽略, 也导致了White方法对实际蒸散的低估, 考虑了植被夜间蒸腾后, 地下水蒸散量估算占观测蒸散总量的比例从70%提高到了90%。
植物蒸腾引起的地下水蒸散是荒漠河岸林地下水消耗的最重要途径, 深入理解地下水蒸散状况, 获取可靠的地下水蒸散数据可以为干旱地区地下水可持续利用及干旱内陆河流域水分配提供参考, 对于维持荒漠河岸林系统正常的生态功能, 维护荒漠绿洲稳定具有重要的意义。
Allen R G, Pereira L S, Raes D, et al, 1998. FAO Irrigation and drainage paper NO. 56 crop evapotranspiration[C]. Rome, Italy, Guidelines for computing crop water requirements.
|
|
Barrongafford G A, Sanchezcañete E P, Minor R L, et al. 2017. Impacts of hydraulic redistribution on grass-tree competition vs facilitation in a semi-arid savanna[J]. New Phytologist, 215(4): 1451–1461.
DOI:10.1111/nph.14693 |
|
Bastiaanssen W G M, Menenti M, Feddes R A, et al. 1998. A remote sensing surface energy balance algorithm for land (SEBAL):1. Formulation[J]. Journal of Hydrology, 212(1/4): 198–212.
|
|
Brunel J P, Walker G R, Kennett-Smith A K. 1995. Field validation of isotopic procedures for determining source water used by plants in a semi-arid environment[J]. Journal of Hydrology, 167: 351–368.
DOI:10.1016/0022-1694(94)02575-V |
|
Butler J J, Kluitenberg G J, Whittemore D O, et al. 2007. A field investigation of phreatophyte-induced fluctuations in the water table[J]. Water Resources Research, 43(430): 299–309.
|
|
Caird M A, Richards J H, Donovan L A. 2007. Nighttime stomatal conductance and transpiration in C3 and C4 plants[J]. Plant Physiology, 143: 4–10.
|
|
Chimner R A, Cooper D J. 2004. Using stable oxygen isotopes to quantify the water source used for transpiration by native shrubs in the San Luis Valley, Colorado, USA[J]. Plant Soil, 260: 225–236.
DOI:10.1023/B:PLSO.0000030190.70085.e9 |
|
Dahm C N, Cleverly J R, Coonrod J E A, et al. 2002. Evapotranspiration at the land/water interface in a semi-arid drainage basin[J]. Freshwater Biology, 47(4): 831–843.
DOI:10.1046/j.1365-2427.2002.00917.x |
|
Dulohery C J, Kolka R K, Mckevlin M R, et al. 2000. Effects of a willow overstorey on planted seedlings in a bottomland restoration[J]. Ecological Engineering, 15(3): 57–66.
|
|
Falge E, Baldocchi D, Olson R, et al. 2001. Gap filling strategies for long term energy flux data sets[J]. Agricultural & Forest Meteorology, 107(1): 71–77.
|
|
Fan J, Oestergaard K T, Guyot A, et al. 2015. Estimating groundwater recharge and evapotranspiration from water table fluctuations under three vegetation covers in a coastal sandy aquifer of subtropical Australia[J]. Journal of Hydrology, 519(PA): 1120–1129.
|
|
Fan J, Ostergaard K T, Guyot A, et al. 2016. Estimating groundwater evapotranspiration by a subtropical pine plantation using diurnal water table fluctuations:Implications from night-time water use[J]. Journal of Hydrology, 542: 679–685.
DOI:10.1016/j.jhydrol.2016.09.040 |
|
Good S P, Noone D, Bowen G. 2015. Hydrologic connectivity constrains partitioning of global terrestrial water fluxes[J]. Science, 349(6244): 175–177.
DOI:10.1126/science.aaa5931 |
|
Gribovszki Z, Kalicz P, Szilágyi J, et al. 2008. Riparian zone evapotranspiration estimation from diurnal groundwater level fluctuations[J]. Journal of Hydrology, 349(1): 6–17.
|
|
Howell T A, Tolk J A, Schneider A D, et al. 1998. Evapotranspira-tion, yield, and water use efficiency of corn hybrids differingin maturity[J]. Agronomy Journal, 90(1): 3–9.
DOI:10.2134/agronj1998.00021962009000010002x |
|
Loheide S P, Butler J J, Gorelick S M. 2005. Estimation of groundwater consumption by phreatophytes using diurnal water table fluctuations:A saturated-unsaturated flow assessment[J]. Water Resources Research, 41(7): 372–380.
|
|
Lubczynski M W. 2009. The hydrogeological role of trees in water-limited environments[J]. Hydrogeology Journal, 17(1): 247–259.
DOI:10.1007/s10040-008-0357-3 |
|
Monteith J L. 1965. Evaporation and environment[J]. Symposia of the Society for Experimental Biology, 19: 205–234.
|
|
Priestley C H B, Taylor R J. 1972. On the assessment of surface heat flux and evaporation using large scale parameters[J]. Monthly Weather Review, 100: 31–92.
|
|
Prieto I, Armas C, Pugnaire F I. 2012. Water release through plant roots:new insights into its consequences at the plant and ecosystem level[J]. New Phytologist, 193(4): 830–841.
DOI:10.1111/j.1469-8137.2011.04039.x |
|
Swinbank W C. 1951. The Measurement of Vertical Transfer of Heat and Water Vapor by Eddies in the Lower Atmosphere[J]. Journal of Meteorology, 8: 135–145.
DOI:10.1175/1520-0469(1951)008<0135:TMOVTO>2.0.CO;2 |
|
Thornthwaite C W. 1948. An approach towards a rational classification of climate[J]. Geographical Review, 38: 55–94.
DOI:10.2307/210739 |
|
Weeks E P, Sorey M L. 1973. Use of finite-difference arrays of observation wells to estimate evapotranspiration from ground water in the Arkansas River Valley, Colorado, U.S[M]. Geological Survey water-supply paper, 27.
|
|
White W N. 1932. A method of estimating ground-water supplies based on discharge by plants and evaporation from soil:Results of investigations in Escalante Valley, Utah, U.S[M]. Geological Survey water-supply paper., 659.
|
|
Wohlfahrt G, Haslwanter A, Hortnagl L, et al. 2009. On the consequences of the energy imbalance for calculating surface conductance to water vapour[J]. Agric For Meteorol, 149: 1556–1559.
DOI:10.1016/j.agrformet.2009.03.015 |
|
Yin L, Zhou Y, Ge S, et al. 2013. Comparison and modification of methods for estimating evapotranspiration using diurnal groundwater level fluctuations in arid and semiarid regions[J]. Journal of Hydrology, 496(2): 9–16.
|
|
Zeppel M, Logan B, Lewis J D, et al. 2013. Why lose water at night? Disentangling the mystery of nocturnal sap flow, transpiration and stomatal conductance-when, where, who?[J]. Acta Horticulturae, 991(991): 307–312.
|
|
高冠龙, 冯起, 张小由, 等. 2017. 蒸散发模型结合微气象数据模拟陆面蒸散发研究进展[J]. 高原气象, 36(6): 1630–1637.
DOI:10.7522/j.issn.1000-0534.2016.00115 |
|
龚家栋, 董光荣, 李森, 等. 1998. 黑河下游额济纳绿洲环境退化及综合治理[J]. 中国沙漠, 18(1): 44–50.
DOI:10.3321/j.issn:1000-694X.1998.01.008 |
|
司建华, 冯起, 鱼腾飞, 等. 2014. 植物夜间蒸腾及其生态水文效应研究进展[J]. 水科学进展, 25(6): 907–914.
|
|
王帅兵, 李常斌, 杨林山, 等. 2015. Budyko方程和单作物系数法在区域蒸散发估算中的耦合及应用[J]. 中国沙漠, 35(3): 683–689.
|
|
杨光超, 朱忠礼, 谭磊, 等. 2015. 怀来地区蒸渗仪测定玉米田蒸散发分析[J]. 高原气象, 34(4): 1095–1106.
DOI:10.7522/j.issn.1000-0534.2014.00114 |
|
尹力, 赵良菊, 阮云峰, 等. 2012. 黑河下游典型生态系统水分补给源及优势植物水分来源研究[J]. 冰川冻土, 34(6): 1478–1486.
|
|
余伟莅, 2013.额济纳胡杨物候节律及生理生态特性研究[D].北京: 北京林业大学.
http://cdmd.cnki.com.cn/Article/CDMD-10022-1013147276.htm |
|
鱼腾飞, 冯起, 司建华, 等. 2017a. 黑河下游柽柳根系水力提升对林分蒸散的贡献[J]. 生态学报, 37(18): 6029–6037.
|
|
鱼腾飞, 冯起, 司建华, 等. 2017b. 胡杨的夜间蒸腾——来自树干液流、叶片气体交换及显微结构的证据[J]. 北京林业大学学报, 39(9): 8–16.
|
|
袁国富, 罗毅, 邵明安, 等. 2015. 塔里木河下游荒漠河岸林蒸散规律及其关键控制机制[J]. 中国科学(地球科学), 45(5): 695–706.
|
|
张武文, 史生胜. 2002. 额济纳绿洲地下水动态与植被退化关系的研究[J]. 冰川冻土, 24(4): 421–425.
DOI:10.3969/j.issn.1000-0240.2002.04.012 |
|
赵春彦, 司建华, 冯起, 等. 2015. 胡杨夜间液流通量及其影响因子研究[J]. 干旱区研究, 32(6): 1173–1180.
|
2. University of Chinese Academy of Sciences, Beijing 100049, China
 2019, Vol. 38
2019, Vol. 38
