2. 成都信息工程大学, 高原大气与环境四川省重点实验室, 四川 成都 610025
云和降水的观测在研究天气变化和气候演变等方面都具有重要意义。在研究云降水的物理机制以及宏微观特性时, 雨滴谱分布, 是人们重点获取的微物理参量之一。雨滴谱分布描述了单位体积空气、单位尺度间隔内的雨滴个数, 是反射率因子、降雨率及液态含水量的计算中最为关键的信息。雨滴谱在空气中的垂直演变直接反映降水粒子在下落过程中的增长和演变, 它指示着云水转化的机制, 为云降水的微物理机制、动力过程提供参照, 在云物理研究和人工影响天气评估中都有重要意义。
20世纪80年代以来快速发展的毫米波雷达是探测云和弱降水三维结构和微物理参数非常重要的手段(刘黎平等, 2016; 姚志刚等, 2018), 和厘米波段的天气雷达相比, 具有更强的探测云和弱降水的能力(刘黎平等, 2014); 此外, 毫米波雷达空间取样体积小, 具有高时空分辨率, 可用于精确探测云的微物理结构。短探测波长极大减少了受湍流影响而造成的谱拓宽, 相比于风廓线雷达、厘米波雷达等(阮悦等, 2018)在云内大气垂直速度、雨滴谱反演等应用方面具有较大优势(吴亚昊等, 2016)。层状云一般产生于大气层结稳定下湿空气的大范围抬升或不规则扰动, 垂直运动一般很微弱, 但层状云内部存在着小尺度在垂直方向连续的气流结构, 而非一些单独的湍流元(Kollias et al, 2000)。这些浅层、微弱、小尺度的垂直运动在层状云、层积云的水成物形成循环中起到关键作用(Shupe et al, 2008)。雷达观测的径向速度中, 既包含了粒子下落速度的贡献, 也包括大气垂直速度的贡献, 准确求取大气垂直速度, 并将垂直运动的作用剔除, 进一步应用于雨滴谱反演是运用毫米波雷达数据反演雨滴谱的基础(Kollias et al, 2002)。王洪等(2017)在运用微雨雷达反演雨滴谱分布中忽略大气垂直速度, 直接从功率谱数据反演雨滴谱。然而, 刘黎平等(2014)在运用毫米波雷达功率谱研究层状云弱降水雨滴谱的研究中, 通过敏感性分析, 证明了雨滴谱反演结果对大气垂直速度的微弱变化十分敏感, 反演雨滴谱时不宜直接忽略它的影响。
Rogers(1964)采用了W-Z方法反演大气垂直速度, W-Z关系是假设在瑞利散射条件、雨滴谱满足指数关系条件下, 而毫米波探测降水大多发生的是Mie散射。Gossard(1994)提出用反卷积的做法将云中粒子的下落末速度和湍流运动分离。这些方法有诸多假设条件, 包括假定雨滴谱分布、粒子下落末速度与直径的关系等, 存在较多不确定性和误差。近年来, Kollias et al(2001)和Shupe et al(2008)运用小粒子示踪法从雷达功率谱中获取大气垂直速度的信息。如Shupe et al(2008)首先确定了液态云粒子的出现, 经过功率谱数据处理后, 确定了用于谱左端表征空气运动的示踪粒子计算了气流速度, 并对功率谱的拓宽情况进行了修正。运用功率谱数据进行处理时, 云中空气湍流、较强水平风运动以及风切变等几种因素导致拓宽功率谱的情况, 影响云内大气垂直速度反演, 给雨滴谱计算带来复杂化。刘黎平等(2014)认为, 虽然空气湍流能拓宽雷达观测的功率谱密度, 但从模拟结果得出, 在有降水的情况下, 空气湍流对功率谱密度的影响可以忽略, 空气湍流对云的功率谱密度有重要影响, 对弱降水则影响不大。
国内彭亮等(2012)利用W-Z关系法结合小粒子示踪法反演了云南腾冲层状云内的大气垂直速度。刘黎平等(2014)利用小粒子示踪法反演了云南腾冲层状云内的大气垂直运动速度, 并对涉及到雨滴谱反演过程中的湍流影响进行了敏感性讨论。郑佳锋等(2016a)详细讨论了功率谱的数据处理方法, 对青藏高原及云内的大气垂直速度进行了反演。另外, Zheng et al(2017)采用该雷达功率谱密度资料反演了大气垂直速度与地面雨滴谱仪推测的结果进行对比发现, 该方法反演的存在一定的可靠性。孙豪等(2017)运用毫米波雷达反演雨滴谱, 并与C波段连续波雷达反演结果进行了对比。
综上所述, 一些雨滴谱反演研究忽略大气垂直速度的影响, 如微雨雷达反演雨滴谱; 有些研究重点反演了云内大气垂直速度, 比如利用小粒子示踪原理的反演研究, 但少有将反演的大气垂直速度结果进一步应用于雨滴谱反演的试验, 雷达数据质量控制、大气垂直速度反演及雨滴谱反演的连贯性研究也较少。毫米波雷达探测的高灵敏度为研究云内大气垂直速度对雨滴谱的影响提供了条件, 功率谱数据提供了更多云内部的微物理特征, 并能充分获取雨滴谱分布在垂直方向上的演变。本文使用Ka波段毫米波雷达获取的功率谱数据进行层状云降水中大气垂直运动和雨滴谱反演, 选取2016年6月4日的层状云降水个例, 分析毫米波雷达、微雨雷达、地面雨滴谱仪功率谱数据的一致性并对比反演的雨滴谱, 从回波强度、大气垂直运动等因素比较雨滴谱的差异。
2 资料和方法 2.1 观测设备和数据中国气象科学研究院灾害天气国家重点实验室于2014-2016年在广东阳江、佛山、龙门等地进行了华南前汛期降水联合探测试验, 本文选用2016年6月龙门地区的层状云降水探测数据, 主要探测仪器包括Ka波段毫米波雷达(CR)、HSC-PS32激光雨滴谱仪、微降水雷达(MRR)。Ka波段毫米波雷达于2013年由中国气象科学研究院联合中国航天科工集团二院第23研究所共同研制, 使用了目前国内外较先进的毫米波技术和信号处理技术, 采用垂直定向的三个模式同时探测, 分别为边界层模式(000模式)、卷云模式(001模式)和降水模式(002模式), 确保对不同类型云都具有良好的探测效果。本文主要采用降水模式的数据。相对于波长较长的天气雷达, CR探测灵敏度高, 具有较强的探测精度和较高的时空分辨率, 可用于云降水精细结构、微物理特征的探测与反演。
HSC-PS32激光雨滴谱仪可以测量出降水过程中所有粒子的粒径大小及对应的粒子下落时的速度, 采用现代激光遥测技术对各种天气过程进行观测记录。微降水雷达(MRR)是垂直指向的调频连续波多普勒雷达, 是测量空中降水雨滴谱的有效工具, 用于进一步反演出雨强、液态水含量等参数。相对于地面雨滴谱仪, MRR具有较高敏感性和较高的时空分辨率, 可以探测到小于传统雨量计最小阈值的降水。但CR相比于MRR具有更高的时、空间分辨率和探测灵敏度。两部雷达主要测量精度参数对比如表 1所示。
| 表 1 CR与MRR雷达主要参数比较 Table 1 The main specifications of CR and MRR |
对毫米波雷达数据进行数据质量控制, 主要包括对功率谱的平滑、噪声电平计算、去噪, 和对反射率因子进行平均、衰减订正等。毫米波雷达数据质量控制是大气垂直速度获取、雨滴谱反演的基础。
2.2.1 数据平滑对数据的初步平滑即求取时间、空间上的平均, 选取3 min的时间平均、210 m高度的空间平均。谱的平滑一定程度上有利于减缓噪声和湍流对后续处理的影响, 选取合适的平滑个数可以有效减小由于湍流、波动等情况造成的不同高度上弱功率分布的不均匀。
2.2.2 去除噪声噪声电平是指功率谱中所有雷达噪声的平均功率, 噪声电平计算的准确性十分关键, 它会直接影响雷达返回信号功率的定标、云信号范围的确定, 常用计算方法有分段法(Petitdidier et al, 1997), Hildebrand and Sekhon方法(Hildebrand et al, 1974), 刘黎平等在国产的行波管毫米波雷达中, 将功率谱大速度大值区的功率作为噪声电平(刘黎平等, 2014)。本文运用Hildebrand and Sekhon方法计算噪声电平。假设雷达噪声属于高斯白噪声, 则满足高斯白噪声的两个统计特性。一是在统计上, 噪声的幅度在频带范围内满足均匀分布, 二是噪声瞬间幅度的概率分布满足高斯分布。当功率谱中存在雷达噪声和气象信号时, 气象信号功率较高, 从高功率开始逐渐将功率谱中的气象信号抽离, 直至只剩下雷达噪声, 计算过程中按抽离后的序列方差是否满足高斯白噪声的方差性质为准则进行判断。在确定噪声电平之后, 将功率谱全段减去噪声电平, 完成去噪过程。
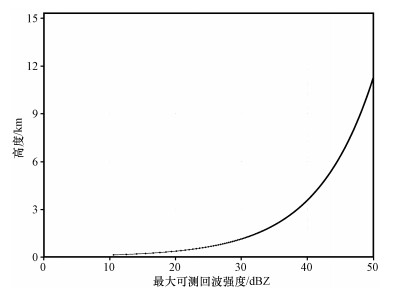
2.2.3 过饱和判断毫米波雷达灵敏度决定了接收机的最小可测接收功率。由于动态范围的限制, 雷达通常只能保证一定范围的有效可测信号。通过对雷达进行接收机动态测试, 结合雷达方程, 可确定不同探测高度上雷达可探测的最大回波强度和最小回波强度。当探测目标回波强度较强, 超过了雷达可测的最大回波范围, 就容易发生回波强度过饱和的现象, 过饱和将导致雷达获取数据不准确, 回波强度小于实际值。雷达观测的回波强度与最大可测回波强度差小于2 dB时判定为过饱和。本次试验中CR最大可测回波强度如图 1所示, 1 km高度处对应最大可测回波强度为29. 67 dBZ, 若此高度回波强度超出27. 67 dBZ即将发生过饱和。
|
图 1 CR不同高度上最大可测回波强度 Fig. 1 The maximum measurable Z of CR at different altitudes |
在使用毫米波雷达探测弱降水时, 回波能量在传播过程中受到云雨粒子和大气的衰减作用严重, 雨滴谱反演过程中, 回波强度作为雨滴谱数浓度的订正参照, 决定了整体数浓度的量级, 通过衰减订正确定更加准确的回波强度是雨滴谱反演的前提。运用逐库法对目标时段回波强度进行衰减订正, 本篇采用K-Z关系计算云降水的衰减系数, K-Z表达式的系数参考樊雅文(2012)通过对外场试验数据的统计分析, 文中按照不同降水强度划分为五个等级, 每个等级分别对应一组不同的K-Z系数, 这样可以在降水时段内的不同强度、云层的不同高度计算更为准确的衰减系数。
2.3 小粒子示踪法反演大气垂直速度毫米波雷达的功率谱数据中, 多普勒速度大小对应着粒子尺寸大小, 功率谱左侧的第一个谱点能够代表雷达所探测到的最小粒子的信号, 如果该粒子足够小, 它自身的下落末速度也非常小, 相对大气的垂直运动速度可以忽略, 作为示踪物来反演大气的垂直运动速度, 称为小粒子示踪法。取功率谱最左端的云信号作为云中空气垂直运动的示踪粒子, 此粒子对应的多普勒速度即代表大气垂直运动的速度。
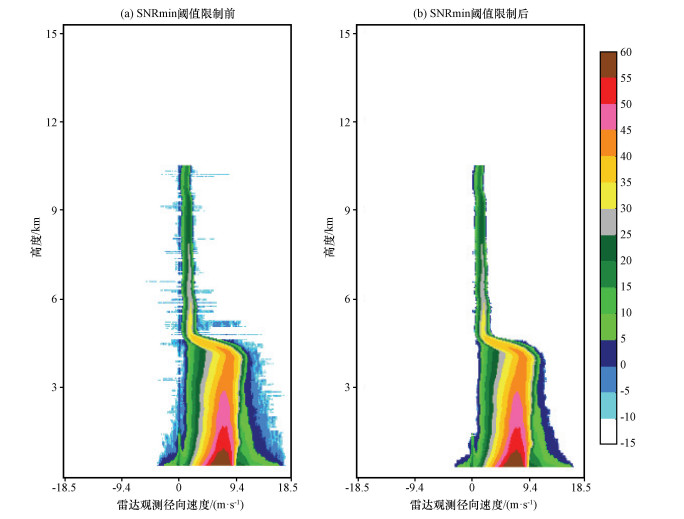
首先获取有效功率谱回波段, 功率谱最左侧的云信号即为示踪粒子。运用Hildebrand and Sekhon方法计算噪声电平进行去噪, 保留下可能代表云信号存在的若干回波段, 选取其中最长、包含全部强信号的功率谱段作为有效回波段。由于受到湍流、风切变以及雷达波束等因素的影响, 功率谱会受到一定拓宽(Shupe et al, 2008), 保留下的功率谱点包含在各个高度上分布不均匀的拉长弱信号, 将造成云信号左端位置的较大误差, 影响垂直速度大小的确定[图 2(a)]。
|
图 2 不同高度的功率谱密度数据(单位: dB) Fig. 2 The Doppler spectral density data of different heights. Unit: dB |
为了确定功率谱云信号左端点, 去除湍流等因素拓宽的弱信号。运用信噪比阈值SNRmin对功率谱数据进行处理。SNR是信噪比, 代表在提取的有效回波段内, 减去噪声电平后的信号值与噪声电平的比值。为云信号的确定设定一个信噪比阈值SNRmin, 对去噪后的信号进行进一步处理:从左右两端的信号速度点开始计算SNR, 当速度点信号的信噪比低于信噪比阈值时SNRmin, 这些信号点不能划入到云信号中而进行剔除, 再依次向功率谱段内部的速度点进行比较和剔除, 直至信号点SNR超过SNRmin, 确定此点为云信号的左端点或者右端点。郑佳锋等(2016a)通过数值模拟的方法, 融合了三种观测模式, 确定当毫米波雷达信号SNR限制为-12 dB时, 由此模拟计算的回波强度和多普勒速度的值与观测值误差极小, 因此设置SNRmin为-12 dB。从图 2(b)中可以看出, 进行信噪比阈值限定后, 各个高度上残留的微弱信号得到有效去除, 各个高度上的云信号端点十分稳定, 不均匀弱信号得到有效消除。进行上述处理后, 功率谱最左端第一个云信号视为示踪粒子, 对应的速度坐标即为大气垂直运动速度。
2.4 雨滴谱反演平移功率谱, 去除大气垂直速度的影响, 得到在静止空气下粒子下落速度对应的功率谱分布, 利用静止空气下的粒子下落末速度对应直径的关系进一步反演雨滴谱。Vr代表雷达观测的径向速度, Vf为粒子在静止空气中的下落末速度, Vr和Vf向下为正, 向上为负; Va为空气垂直运动速度, 设向上为正, 向下为负, 雷达观测的粒子下落速度等于静止空气粒子下落速度与空气垂直运动速度之和:
| $ {{V}_{\text{f}}}={{V}_{\text{r}}}+{{V}_{\text{a}}}~, $ | (1) |
确定功率谱左端信号对应的谱点脉冲数Num, pulsenum为每条功率谱的谱点总数, 本次实验中为256, Nyquist为最大不模糊速度, 降水模式下为-18. 54 m·s-1, 对应大气垂直速度为:
| $ {{\mathit{V}}_{\text{a}}}\text{=-}\left(\text{Num-pulsenum/2} \right)\text{ }\!\!\times\!\!\text{ Nyquist }\!\!\times\!\!\text{ 2/pulsenum, } $ | (2) |
用平移后的功率谱直接反演雨滴谱存在如下转换(刘黎平等, 2014):
| $ \begin{align} &{{S}_{\text{Z}}}({{V}_{\text{r}}})\text{ }=\text{ }\!\!|\!\!\text{ }\frac{\partial Z}{\partial {{V}_{\text{r}}}}|~=\text{ }\!\!|\!\!\text{ }\frac{\partial Z}{\partial ({{V}_{\text{f}}}-{{V}_{\text{a}}})}\text{ }\!\!|\!\!\text{ }=|\frac{\partial Z}{\partial {{V}_{\text{f}}}}| \\ &~=|\frac{\partial Z}{\partial D}\text{ }\cdot \frac{\partial D}{\partial {{V}_{\text{f}}}}|\ \ \, ~ \\ \end{align} $ | (3) |
因此功率谱数据与雨滴谱存在如下对应关系, 由此获取雨滴谱分布N(D):
| $ {{S}_{Z}}({{V}_{\text{r}}})=N\left(D \right){{\sigma }_{\text{bsc}}}\left(D \right)\cdot \frac{\partial D}{\partial {{V}_{\text{f}}}}~, $ | (4) |
毫米波雷达观测弱降水时粒子发生米散射, 计算Mie散射后向散射截面, 代入公式(4)。雨滴谱是个数关于粒子直径的分布函数, 用功率谱数值除以每个粒子的截面以获取雨滴个数的分布时, 需要乘以下落末速度关于直径的微分, 将雨滴谱个数关于下落末速度的分布转化为关于粒子直径的分布, 才能够满足雨滴谱的定义。中间的转换依赖于V-D关系表达式(Gossard, 1994):
| $ D=\left\{ \begin{align} &1/4{{V}_{\text{f}}}\times {{(\rho /{{\rho }_{0}})}^{0.\text{ }5}}~, \text{ }({{V}_{\text{f}}}\le 2.\text{ }5\text{ }\!\!~\!\!\text{ m }\!\!\cdot\!\!\text{ }{{\text{s}}^{-1}})\text{ } \\ &-1.\text{ }667\text{ln}~\left[ \frac{9.\text{ }65-{{V}_{\text{f}}}\times \text{ }{{\left(\frac{\rho }{{{\rho }_{0}}} \right)}^{0.\text{ }4}}~}{10.\text{ }3\text{ }} \right], \text{ }({{V}_{\text{f}}}>2.\text{ }5~\text{m}\cdot {{\text{s}}^{-1}}) \\ \end{align} \right.\text{ }~ $ | (5) |
式中: ρ0为地面的空气密度; ρ为探测高度处的空气密度; ρ/ρ0由高度和地面温度、大气温度垂直递减率等量共同决定, 在研究的高度范围较低的情况下, 可简化成只与高度变化有关的简单函数。
对雨滴谱数值进行计算之后, 用Ka波段毫米波雷达订正后的回波强度修正反演的雨滴谱数浓度, 回波强度对于雨滴谱整体量级有着指示意义。Ulbrich(1983)认为, 使用三个参数的Gamma分布对雨滴谱分布(DSD)的描述更具有普适性, 郑娇恒等(2007)也对比了雨滴谱中的M-P分布和Gamma分布。因此本文运用Gamma分布对反演结果进行拟合。为了确定雨滴谱的固有形状, 使形状参数独立于含水量LWC和质量加权平均直径Dm, 对Gamma分布进行标准化处理, 表达式为:
| $ N\left(D \right)={{N}_{\text{w}}}f\left(\mu \right)\text{ }{{\left(\frac{D}{{{D}_{\text{m }\!\!~\!\!\text{ }}}} \right)}^{\mu }}\text{exp}~\left[ -\left(\mu +4 \right)\frac{D}{{{D}_{\text{m }\!\!~\!\!\text{ }}}} \right]\text{ }, $ | (6) |
| $ f\left(\mu \right)=\frac{6}{256}\times \frac{{{\left(\mu +4 \right)}^{\mu +4}}~}{\Gamma \left(\mu +4 \right)~}, ~ $ | (7) |
标准化Gamma函数后的三个参数都具有明确的物理意义: Dm代表了质量加权平均直径; Nw是标准化截距参数, 表征有着相同中值体积直径和相同液态水含量LWC的指数分布下的截距参数, 代表整体数浓度量级; 参数μ独立于Dm、Nw, 只与雨滴谱分布形状有关。Nw和Dm相互影响, 在相同含水量条件下, Dm越大, 粒子集中的尺寸就越大, 少数大粒子便会占据较多水分, 相应导致整体数浓度的量级下降。运用阶矩法拟合标准化Gamma分布中的三个独立参数, Nw, μ和Dm可以通过雨滴谱分布的三阶、四阶和六阶矩进行描述(Testud et al, 2001)。
3 个例分析选取2016年6月4日龙门地区的层状云降水过程进行大气垂直速度、雨滴谱的反演和分析。6月4日层状云降水由对流发展的积状云演变而来, 14 : 50(北京时, 下同)-15 : 20阶段内对流云强烈发展又很快消散, 在地面产生了较弱降水。之后云层发展并趋于稳定, 延伸高度达到11 km, 逐渐形成稳定的层状云降水。层状云降水的主要集中时段为16 : 15-18 : 35, 按照地面激光雨滴谱仪测量雨滴谱数据计算雨强, 起始阶段雨强维持在2 mm·h-1左右, 17 : 00之后地面雨强逐渐减小, 17 : 33减小至0. 5 mm·h-1以下, 18 : 35左右层状云降水逐渐停止。层状云降水接地, 云顶高度维持在11 km左右, 18 : 00之后逐渐下降在10 km左右。个例分析首先给出回波强度、径向速度的演变情况, 反演云降水大气垂直速度并用基数据大体验证反演的结果; 然后进行毫米波雷达、微雨雷达、地面雨滴谱仪探测回波强度的对比, 在确定功率谱一致性基础上进行雨滴谱的反演, 并从回波强度变化、大气垂直速度的影响等方面讨论雨滴谱变化。
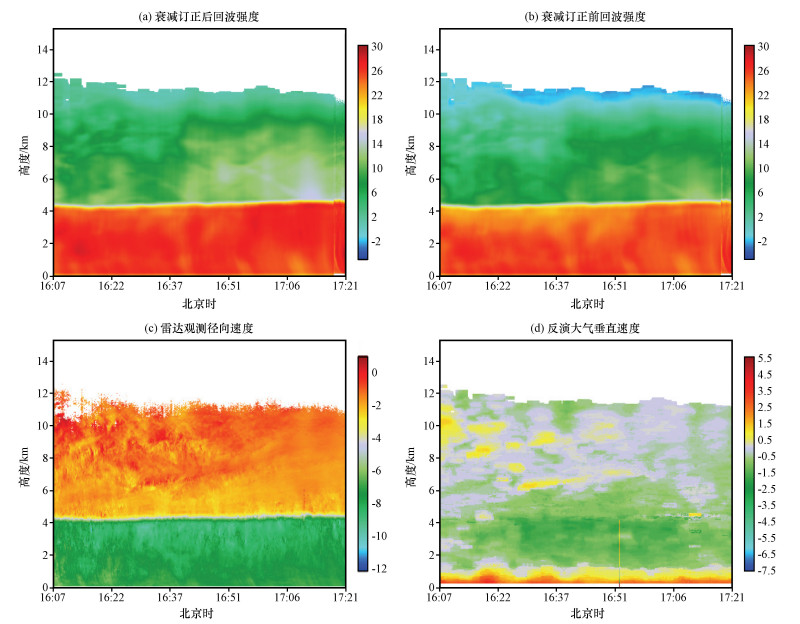
3.1 大气垂直速度反演 3.1.1 反演结果2016年6月4日层状云降水阶段内选取较稳定的降水阶段16 : 07-17 : 21, 对回波强度进行衰减订正, 如图 3(b)为衰减订正前, 图 3(a)为衰减订正后回波强度随高度的分布的演变, 订正后的回波强度在各个高度都有所增大, 根据上文中的过饱和判定条件, 近地面1 km左右可能发生回波强度过饱和现象。
|
图 3 2016年6月4日16 : 07-17 : 21各物理量时间-高度演变图 Fig. 3 The time-height sections of Z before and after attenuation correction (unit: dBZ), the radial velocity (unit: m·s-1), vertical air motions (unit: m·s-1) from 16 : 07 to 17 : 21 on 4 April 2016 |
对功率谱数据进行平滑、去噪处理后, 按照小粒子示踪法对整个降水时段进行垂直速度的反演, 结果如图 3(d), 图中上升速度为正, 下沉速度为负。约4. 2 km高度为零度层, 约1 km到零度层高度之间为明显连续的大片下沉运动, 零度层以上云体内部微弱的上升和下沉运动并存。近地面约1 km以下为较为明显的上升运动, 上升速度达到3~4 m·s-1, 层状云降水中在近地面一般不会出现如此大的上升气流, 近地面大气垂直速度的反演出现偏差。
用雷达观测径向速度随着时间的演变图[图 3(c)]大致验证大气垂直速度反演的结果, 此时间段降水较稳定, 回波强度值变化很小, 粒子本身下落末速度较稳定。在零度层高度以下、1. 5 km之上出现较大的观测粒子径向速度区, 尤其在16 : 25-17 : 06时间段内, 在2. 0~4. 2 km高度范围出现径向速度值更大的亮色区域, 代表更大的落速, 与大气垂直速度图中[图 3(a)]此时间、高度段内的较强下沉气流对应, 说明在回波强度变动很小的情况下, 较强的下沉气流加快了降水粒子的下落。
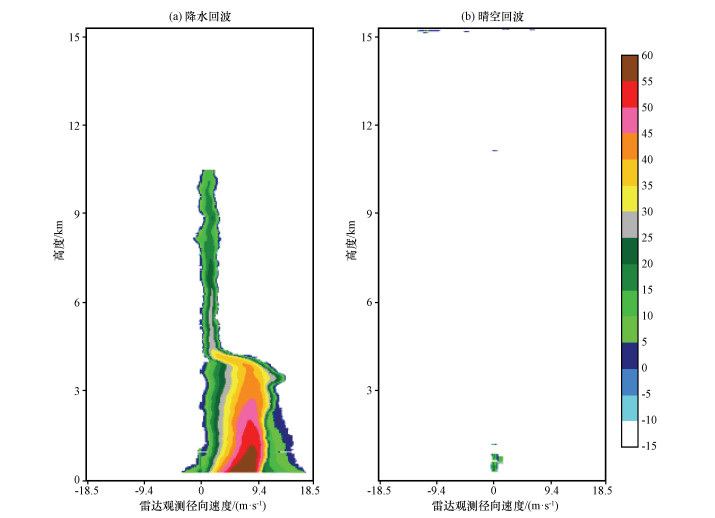
3.1.2 近地面偏差原因分析反演大气垂直速度的过程中, 近地面较大的上升速度是由于功率谱在近地面的异常导致的。降水时段内, 近地面功率谱的左端点位置偏左, 且在零速度附近产生了一个较为明显的回波凸起[图 4(a)], 可能由非气象杂波导致。晴空状态下在近地面经常出现不均匀分布的点状回波和直线型回波, 主要由大气浮游粒子(Lhermitte, 1996)和雷达直流径向干扰引起(郑佳锋等, 2016b)。选取降水之前无云时段, 对晴空回波的功率谱进行去噪滤波处理[图 4(b)]出现以下特征:晴空回波状态下, 近地面约1. 5 km以下, 在零速度附近出现谱回波, 谱宽度较窄, 强度较弱。
|
图 4 不同高度的功率谱密度数据(单位: dB) Fig. 4 The Doppler spectral density data of different heights. Unit: dB |
从图 4(b)中可以看出, 功率谱分布在零速度附近, 能量较高的集中在零速度左右两个速度点内(约-0. 1448, 0和0. 1448 m·s-1), 大多数值分布在5~15 dB之间, 大于15 dB的点也较多, 影响高度延伸至约1. 2 km的高度。从图 4(a)中可以看出, 零速度附近出现了明显高于周围能量的回波点, 在约1. 2 km以下能量值大多为10 dB以上, 集中于13~17 dB之间, 与上述晴空状态下功率谱的量级、位置、高度都大致对应。因此, 考虑晴空状态下的大气浮游粒子、直流径向干扰, 经过时间平均以及毫米波雷达本身的特征的影响, 在探测降水中导致了零速度附近功率谱值的突变和拓宽。它的出现, 使得原本停留在零速度附近的左边界向左拓展, 1. 2 km左右高度以下云信号的起始位置偏左边, 停留在负速度区即上升速度。晴空回波干扰影响的高度约1. 2 km, 此高度以上功率谱恢复了正常的左边界, 云信号左端可能快速由负速度区转移到正速度区, 反演的大气垂直速度在此高度有一个由负到正的速度突变(图 8)。
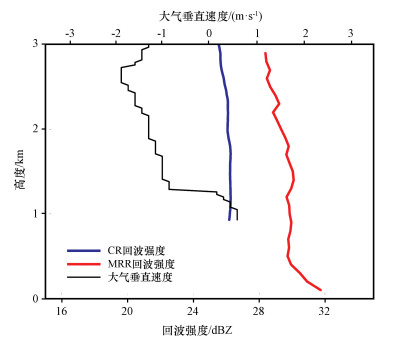
|
图 8 2016年6月4日16 : 51 CR、MRR回波强度和大气垂直速度廓线 Fig. 8 The vertical profiles of Z and vertical air motions for CR, MRR at 16 : 51 on 4 April 2016 |
此外, 根据最大可测回波强度的曲线, 判定并剔除反演过程中可能受到过饱和现象影响的区域, 近地面约1 km范围内都可能受到过饱和的影响, 可能导致近地面功率谱的异常。
综合以上两点原因, 反演近地面大气垂直速度出现偏差, 将为雨滴谱反演带来巨大的误差, 因此进一步对比分析雨滴谱时, 取样高度以及雨滴谱演变的讨论应尽可能选取在1 km以上, 将涉及到过饱和现象的数据予以剔除, 未受过饱和影响的近地面区域仍存在弱上升速度。
3.2 雨滴谱反演 3.2.1 回波强度一致性对比雨滴谱反演时回波强度大小决定了雨滴谱数浓度量级, 将毫米波雷达反演结果与微雨雷达、地面雨滴谱仪对比时应首先考虑仪器测量回波强度的差异。毫米波雷达测量回波强度在近地面发生过饱和现象, 将出现过饱和的数据剔除, 为此选择1 km高度处的回波强度进行对比。
比较整个降水时段CR、MRR测量高空1 km处回波强度和地面雨滴谱仪测量回波强度的差异。从图 5中可以看出, 16 : 09-17 : 09为降水稳定时期, MRR回波强度高于CR 3~5 dBZ, 整体回波减弱时CR的回波强度反超MRR, 在17 : 35-18 : 29时CR回波强度高于MRR约3 dBZ; 地面雨滴谱仪测量回波强度随时间变动幅度较大, 但时间序列基本和MRR回波强度值对应起来, 回波强度值在MRR回波强度序列附近上下波动, MRR回波强度值更接近地面雨滴谱仪测量情况。
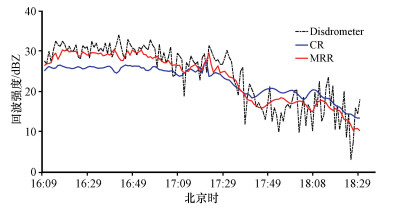
|
图 5 1. 0 km高度上CR、MRR观测回波强度和Disdrometer探测地面回波强度时间序列 Fig. 5 Time series of Z observed by CR and MRR at 1. 0 km and Z observed by Disdrometer at ground surface |
温龙等(2015)分析南京地区两次夏季降水过程, 表明MRR与地面雨滴谱仪2DVD观测降水回波强度、粒子浓度分布的观测结果都较为一致, MRR对层状云弱降水的探测结果优良, 其中, MRR时间分辨率为10 s, 2DVD为3 s。王洪等(2017)认为MRR和THIES雨滴谱资料的反射率因子的变化趋势和幅度相近, 但离散程度大, 两个仪器的时间分辨率都是1 min。谢蕾等(2014)表明CR探测回波强度相较于HSC-PS32雨滴谱仪观测弱降水来说变化趋势大致相同但变化幅度差异较大, 回波强度差值从几到十几不等, 雷达天线的积水是误差的主要来源, 仪器时间分辨率与本文相同。
文中MRR和地面雨滴谱仪的平均回波强度大小、总体变化趋势较为一致, 但存在较大离散, 由于雨滴谱仪的时间分辨率不同, 和温龙等(2015)结果有差异, 与王洪等(2017)结果类似; CR和地面雨滴谱仪相比, 在测量较强降水时回波强度偏低, 在测量较弱降水时回波强度偏高, 与MRR相比和地面测量值的偏差变动更大, 与谢蕾等(2014)结论相同。本文结果与上述研究结果类似, 回波强度偏差考虑由回波衰减、米散射效应、雷达天线积水等因素造成。
3.2.2 CR与MRR雨滴谱反演对比(1)回波强度谱一致性比较
MRR为CR提供整个高度上的雨滴谱对比, 首先需要确定两者对应的功率谱具有一致性。结合表 1中的仪器参数, 经计算垂直观测情况下MRR的空间取样体积约CR的80倍, MRR的时间分辨率低, 约为CR的20倍。因此, CR探测区域集中的很小, 能够探测降水过程中的精细结构, 而MRR倾向于反演一段时间、空间内的平均状况。首先对CR的功率谱进行时间、空间上的平均, 寻找降水情况稳定的时刻, 使局部更接近整体平均, 两种雷达在不同取样体积的情况下才可能具备功率谱的一致性。
将功率谱按照雷达方程转化成回波强度谱。由于MRR和CR回波强度的差异存在, 而MRR探测回波强度相对准确, 对毫米波雷达的回波强度谱型进行强度订正, 来消除两个仪器回波强度的固有偏差, 只比较两者回波强度谱的形状、左右位置的差异。强度订正时将回波谱值整体移动, 使CR谱峰的回波强度值与MRR回波谱峰值相同。在降水的各个阶段的对比情况有变化, 降水逐渐加强或者减弱消散的阶段, 两个仪器回波功率谱形状、左右位置差异较大。在降水稳定时期, 回波强度谱整体平滑, 波动较少, 两仪器回波功率谱形状对应的很好。在2016年6月4日的层状云降水时段, 选取回波强度谱对比较为一致的16 : 51时刻, 在0. 9, 1. 2, 1. 8和2. 1 km几个高度进行回波谱比较, 900 m以上功率谱数据不受到过饱和的影响。
从图 6中可以看出, CR和MRR功率谱在各个取样高度上形状、左右位置对应得很好, 在1. 8 km处左右位置稍有偏差。由于CR探测灵敏度更高, 回波谱向两端延伸更长, 比MRR谱更宽, 两者在谱峰的主要集中区的形状、位置均十分吻合, 因此CR和MRR回波强度谱具有一致性, 在此基础上进行雨滴谱的反演。
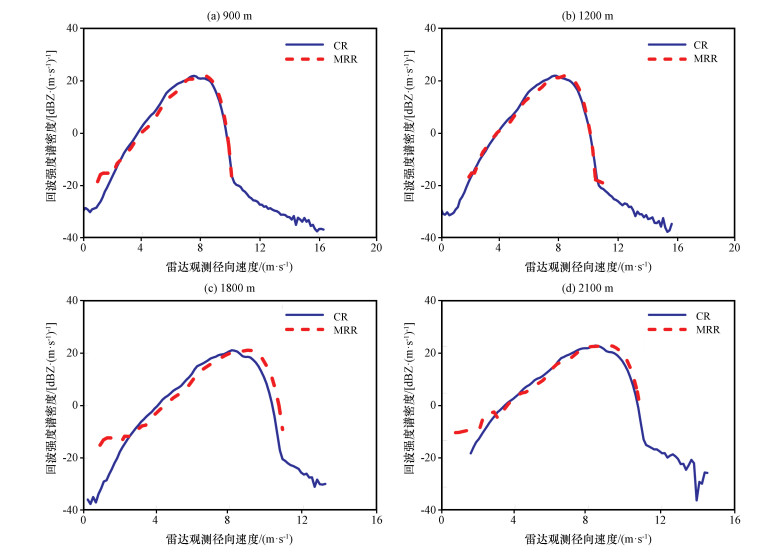
|
图 6 2016年6月4日16 : 51 CR、MRR回波强度谱对比 Fig. 6 The Z spectrum contrast of CR, MRR at different heights at 16 : 51 on 4 April 2016 |
(2)雨滴谱反演比较
运用毫米波雷达, 引入大气垂直速度的反演结果计算雨滴谱在整个高度上的分布。为了分析回波强度、大气垂直速度和回波强度谱对比情况等因素对于雨滴谱反演结果的影响, 设计了三个不同的实验。试验1(T1):运用毫米波雷达功率谱数据, 订正后的毫米波雷达回波强度并引入大气垂直速度结果进行雨滴谱反演; 试验2(T2):不引入大气垂直速度结果, 其他与T1相同; 试验3(T3):不引入大气垂直速度结果, 用衰减订正后的MRR回波强度代替CR回波强度, 其他与T1相同; 这些试验结果与MRR反演雨滴谱结果进行比较。
首先分析16 : 51时刻雨滴谱反演试验情况(图 7)。T1和T2的比较中, 对照大气垂直速度廓线(图 8), 0. 9~1. 2 km之间为正上升气流, 1. 2 km以上迅速转变为下沉气流, 下沉气流速度随高度增大而逐渐减小。因此引入垂直速度时, 0. 9~1. 2 km功率谱整体右移, T1相比于T2雨滴谱的集中半径变大、量级变小, 1. 2 km以上功率谱左移, T1相比于T2粒子整体半径减小, 数浓度量级变大。雨滴谱反演结果对大气垂直速度结果的引入较敏感, 考虑了大气垂直速度的T1实验, 雨滴谱随着高度降低呈现整体半径变大、数浓度量级减小的演变趋势。
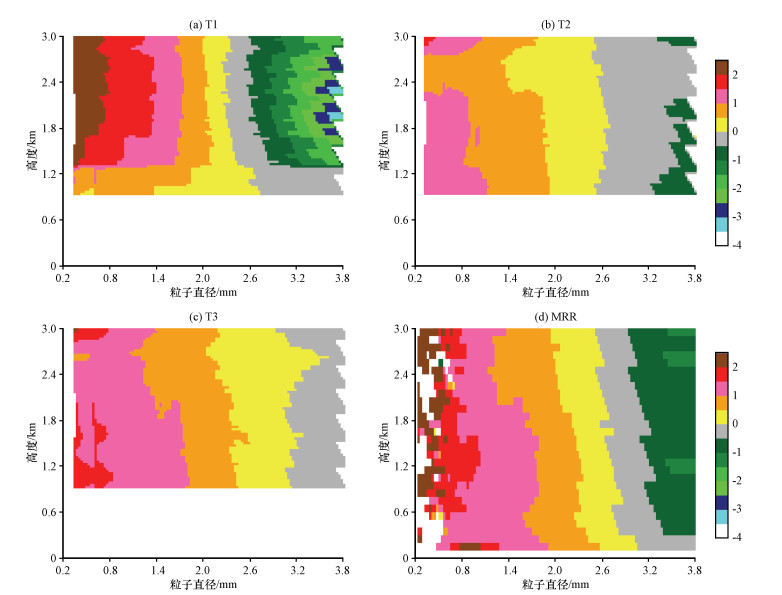
|
图 7 2016年6月4日16 : 51各个高度上T1、T2、T3试验和MRR雨滴谱分布数浓度的对比[单位:(mm·m3)-1] Fig. 7 Raindrop size distributions at different altitudes of T1, T2, T3 and MRR at 16 : 51 on 4 April 2016. Unit: (mm·m3)-1 |
T2与T3的比较中, 回波强度廓线(图 8)中MRR与CR回波强度在各个高度上存在差异, MRR回波强度的引入增大了回波强度, T3相比于T2雨滴谱整体量级增大。T3与MRR在回波强度相同、均不考虑大气垂直速度的情况下, 分别使用CR和MRR的功率谱数据进行雨滴谱反演(见图 6), 各个高度功率谱对比大体具有一致性。在不受过饱和影响的高度, T3与MRR对比中MRR雨滴谱结果中小粒子数浓度更大, 但雨滴谱量级、分布都大致对应, 由此验证雨滴谱反演方法合理性。
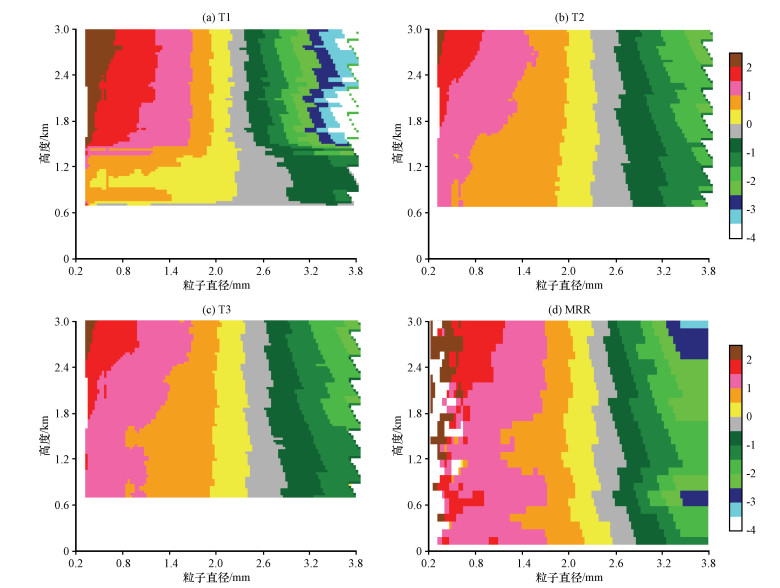
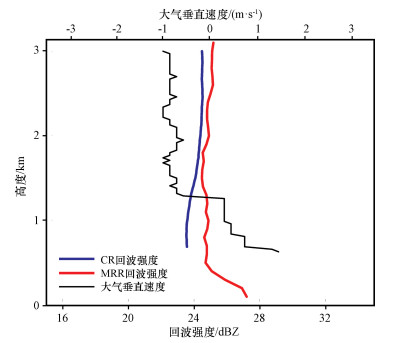
另一时刻17 : 28的雨滴谱反演中(图 9), 大气垂直速度、回波强度廓线(图 10)显示, 0. 8~1. 2 km为上升气流, 1. 3 km以上为下沉气流, 且这个时刻毫米波雷达和微雨雷达回波差异减小, 在高空回波强度逐渐靠近。T1中雨滴谱分布在1. 4 km以上为较为均匀的雨滴谱分布, 由于反演的正大气速度, 0. 7~1. 4 km之间雨滴谱量级减小; 两个仪器的回波强度差别很小, 因此T2与T3雨滴谱结果差别不大。同样在功率谱一致性较好的情况下, T3与MRR反演雨滴谱分布结果大致对应, 雨滴谱数整体量级、数浓度分布都基本对应, 很好的验证功率谱反演方法的正确性。由于1200 m和1800 m高度处回波功率谱的左右位置存在偏差, 也使得T3与MRR中雨滴谱在这两个高度略有差异。
|
图 9 2016年6月4日17 : 28各个高度上T1、T2、T3试验和MRR雨滴谱分布数浓度的对比[单位:(mm·m3)-1] Fig. 9 Raindrop size distributions at different altitudes of T1, T2, T3 and MRR at 17 : 28 on 4 April 2016. Unit: (mm·m3)-1 |
|
图 10 2016年6月4日17 : 28时刻CR、MRR回波强度和大气垂直速度廓线 Fig. 10 The vertical profiles of Z and vertical air motions for CR, MRR at 17 : 28 on 4 April 2016 |
综上所述, T1中毫米波雷达反演雨滴谱结果对于大气垂直速度的引入十分敏感, 由于垂直气流在整个高度上的转变, 雨滴谱也随着高度发生演变, 随着高度降低整体数浓度量级逐渐减小、但谱变宽、半径增大, 与MRR相比充分体现了空气垂直运动对雨滴谱的影响。
T3运用MRR回波强度代替CR进行反演使得雨滴谱量级发生改变, 说明回波强度大小改变雨滴谱反演整体量级。T3和MRR反演的回波强度、大气垂直速度条件相同, 在CR和MRR功率谱对比一致的基础上, 两个仪器反演的雨滴谱分布在各个高度上类似, 由此验证了在不考虑大气垂直速度时, 运用CR功率谱数据直接反演雨滴谱方法的合理性。
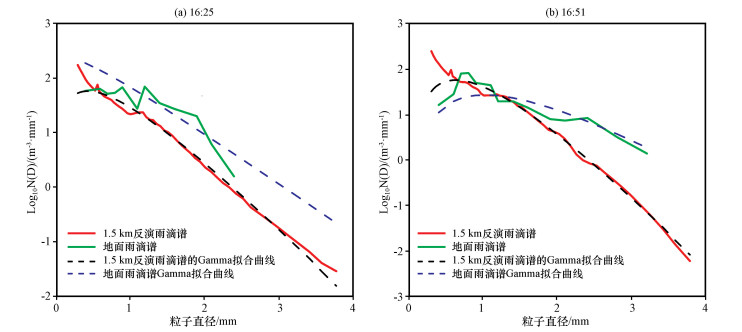
3.2.3 CR反演与地面雨滴谱仪对比毫米波雷达引入大气垂直速度的反演, 用地面雨滴谱仪的雨滴谱分布为毫米波雷达反演的雨滴谱做参照。由于大气垂直速度反演结果在1. 5 km以下存在上升速度偏大以及上升气流到下沉气流的突变的问题, 又考虑到稳定降水阶段, 地面至1. 5 km的回波强度和雨滴谱变化都不大, 选取1. 5 km处毫米波雷达反演的雨滴谱, 和地面雨滴谱采样数据进行比较。从图 11中可以看出, 1. 5 km处CR反演雨滴谱(图中红色实线)与地面雨滴谱(图中绿色实线)对比, 量级、形状都较为接近, CR反演的大粒子的数浓度量级较小, 小粒子端的数浓度量级较大, 整体粒子的平均直径较小; 地面雨滴谱呈现两端数浓度小、中间直径数浓度大的分布特点。对CR反演雨滴谱曲线、地面雨滴谱分布曲线分别进行标准化Gamma拟合[图11(a)、(b)中黑色、蓝色的虚线]。与反演雨滴谱曲线相比, 拟合曲线在小滴端的数量级偏小, 在中间尺度和大滴端部分与反演雨滴谱十分贴近。
|
图 11 CR反演1. 5 km和地面的雨滴谱及其Gamma拟合曲线的对比 Fig. 11 Comparisons of DSD get by CR and its Gamma fitting curve at 1. 5 km and at ground |
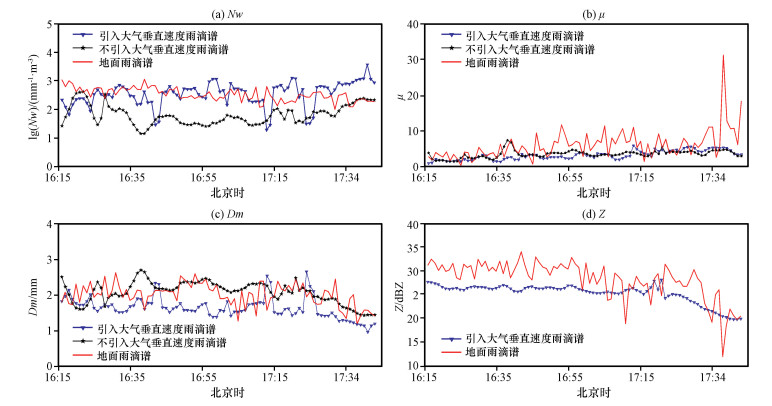
地面雨滴谱仪统计的雨滴谱分布由于取样直径的间隔较大, 分布不够精细, 且仪器灵敏度限制只能测量精确到0. 1个雨滴的精确度; CR反演的雨滴谱延伸为一条较为平滑的曲线, 由于测量的高灵敏度, 可以反演较小的数浓度量级。因此, 由于仪器的灵敏度差异, 获取的雨滴谱形状μ存在着固有的差异; 为了更好对比毫米波雷达反演的雨滴谱和地面雨滴谱的对比情况, 计算拟合参数每分钟的时间序列(图 12), 将CR在引入(T1试验, 蓝色实线带三角号)和不引入大气垂直速度(T2试验, 黑色实线带五角星)结果时反演的1. 5 km高度的雨滴谱与地面雨滴谱(红色实线)的拟合参数Nw、μ和Dm对比, 并给出CR测量1. 5 km高空和地面雨滴谱仪测量地面的回波强度的对比(图 12)。
|
图 12 2016年6月4日雨滴谱拟合参数的时间序列对比 Fig. 12 Time series of fitting parameters of DSD on 4 April 2016 |
从图 12中可以看出, 不引入大气垂直速度时, CR反演雨滴谱数参数Nw与地面雨滴谱相比低了一个数量级, 集中在1~2之间, Dm与地面雨滴谱处于同一数量级。造成偏低的原因一部分源于毫米波雷达在1. 5 km和地面雨滴谱回波强度的差异。
从图 10中可以看出, 引入大气垂直速度时, CR反演与地面雨滴谱仪Nw值处于同一量级上下波动, 多集中在2~3之间。Dm集中值相对于地面雨滴谱偏小, 在1. 6~2 mm, 在某些时刻Dm值较大达到3 mm左右。引入大气垂直速度后, CR反演的1. 5 km处的雨滴谱相对于地面的数浓度量级相当, 粒子平均直径较小。
形状参数μ独立于Dm和Nw, 只与雨滴谱分布的形状有关。从图 10和12对比可以看出, 在引入和不引入大气垂直速度的两种情况下, 毫米波雷达的μ随着时间变化平稳, 数值集中在2~5之间; 地面雨滴谱的形状参数随着时间变动剧烈, 在0~10之间变动, 在17 : 38时出现了超出正常雨滴谱形状参数范围的极端值, 达到31. 23。根据Yahao et al(2017)统计的华南地区层状云降水三个参数的统计特征, 较弱的层状云降水形状参数较大, 可能超过10, 但基本不会有超过20的情况。出现17 : 38时刻回波强度由25. 95 dBZ骤然减小到11. 81 dBZ, 降水强度骤减为0. 08 mm·h-1, 而前后两个时刻降水强度分别为0. 468 mm·h-1和0. 217 mm·h-1, 骤减的雨量造成了雨滴谱分布的异常。地面雨滴谱仪收集雨滴谱具有较大不稳定性, CR反演雨滴谱相较于地面雨滴谱的形状参数更集中、随着时间变化更加稳定。
参数Dm和Nw之间相互影响, 参数Nw计算公式中Nw与Dm成反比关系。在参数序列的统计结果中, Nw越大的时刻对应的Dm越小, 存在着明确的负相关关系。在相同含水量条件下, Dm越大, 由较大粒子占据的后向散射能量的比率越多, 少量大粒子占据大量总体的后向散射能量, 整体粒子数浓度量级偏低, 因而Nw值越低。
从统计结果来看, 地面雨滴谱仪测量地面雨滴谱的拟合参数表征的雨滴谱形状、量级随之时间的变化都较为剧烈, 对于较弱、逐渐减弱的降水, 地面雨滴谱仪对雨滴的收集能力不高, 探测精度低; 毫米波雷达反演雨滴谱随着高度的变化, 反演结果也为稳定, 即使是弱降水, 仍能对雨滴谱进行有效的反演。引入大气垂直速度的反演在1. 5 km相对于地面, 雨滴谱整体量级相当, 但集中的粒子直径较小。
4 结论与讨论使用Ka波段毫米波雷达获取的功率谱数据进行层状云降水中大气垂直速度和雨滴谱反演, 选取2016年6月4日的层状云降水个例, 分析毫米波雷达、微雨雷达、地面雨滴谱仪功率谱数据的一致性并对比反演的雨滴谱, 从回波强度、大气垂直速度等因素比较雨滴谱的差异。得到以下主要结论:
(1) 运用小粒子示踪法反演云内大气垂直速度, 1 km以上到零度层之间存在弱的下沉速度, 速度大小在0. 5~1. 5 m·s-1之间; 近地面约1 km以下垂直速度接近零, 有时存在弱上升速度。1 km以下近地面由于受到大气浮游物和雷达直流干扰回波的影响以及过饱和现象, 功率谱在零速度附近出现回波, 谱拓宽而导致云信号左端点异常偏左, 使较低高度层数据反演的大气垂直速度出现偏差。大气垂直速度的引入对雨滴谱反演影响十分明显, 导致整个功率谱平移, 从而影响粒子的集中半径大小和整体量级。
(2) 经过回波强度时间序列的比较, 毫米波雷达CR、微雨雷达MRR和地面雨滴谱仪测量回波强度存在系统差异, 由于衰减严重、天线罩积水等原因使得CR回波强度数据相较于其他仪器误差较大, MRR回波强度和地面雨滴谱测量回波强度对应较好。
(3) CR反演与MRR对比时, 首先比较两者功率谱, CR相对于MRR获取的功率谱更宽, 两者在谱峰主要集中区域的形状、左右位置基本对应, 但不同时刻、高度均有出现左右位置的略微偏差。
(4) 为了比较回波强度、大气垂直速度引入因素对CR和MRR反演雨滴谱的影响, 进行T1、T2、T3试验与MRR雨滴谱结果对比可知: ①CR反演雨滴谱结果对于大气垂直速度的引入十分敏感, 由于大气垂直气流在整个高度上的转变, 雨滴谱也随着高度发生演变, 随着高度降低整体数浓度量级逐渐减小、但谱变宽、半径增大。②回波强度大小改变雨滴谱反演整体量级。③当CR和MRR功率谱在各个高度对应良好, 在同样不考虑大气垂直速度、回波强度相同的条件下, 反演雨滴谱一致, 验证了反演方法的正确性。
(5) CR反演1. 5 km低空雨滴谱与地面雨滴谱拟合参数对比, 形状参数μ集中在2~5之间, 相比于地面雨滴谱集中而稳定, 不引入大气垂直速度时Nw与地面雨滴谱相比低了一个数量级, Dm与地面雨滴谱大小相当; 引入大气垂直速度后, Nw与地面雨滴谱数量级相当, Dm值集中在1. 6~2 mm, 相比于地面值较小。
运用毫米波雷达功率谱特性可以有效获取层状云内的空气垂直运动速度, 用功率谱能够直接反演层状云降水雨滴谱在各个高度上的分布情况, 将反演的大气垂直速度引入功率谱, 可以获取雨滴在静止空气下的运动状态, 获取更加准确的雨滴谱分布。获取大气垂直速度、反演雨滴谱的手段本身十分稀少, 毫米波雷达的功率谱是有效的工具。但本文反演的大气垂直速度采用回波强度和雷达径向观测速度大致验证, 目前缺乏准确验证的手段。此外, 由于毫米波雷达功率谱本身特性, 近地面1 km以下获取的大气垂直速度偏大, 因此在后续雨滴谱反演中不考虑近地面1 km以内的反演。如何减少这部分的影响是今后工作的方向。
Gossard E E. 1994. Measurement of cloud droplet size spectra by Doppler Radar[J]. Journal of Atmospheric & Oceanic Technology, 11(3): 712–726.
|
|
Hildebrand P H, Sekhon R S. 1974. Objective determination of the noise level in Doppler spectra[J]. Journal of Applied Meteorology, 13(7): 808–811.
DOI:10.1175/1520-0450(1974)013<0808:ODOTNL>2.0.CO;2 |
|
Kollias P, Albrecht B A. 2000. The turbulence structure in a continental stratocumulus cloud from millimeter-wavelength Radar observations[J]. Journal of the Atmospheric Sciences, 57(57): 2417–2434.
|
|
Kollias P, Albrecht B A, Marks F. 2002. Why Mie?[J]. Bulletin of the American Meterological Society, 83(10): 1471–1483.
DOI:10.1175/BAMS-83-10-1471 |
|
Kollias P, Albrecht B A, Lhermitte R, et al. 2001. Radar observations of updrafts, downdrafts, and turbulence in fair-weather cumuli[J]. Journal of the Atmospheric Sciences, 58(13): 1750–1766.
DOI:10.1175/1520-0469(2001)058<1750:ROOUDA>2.0.CO;2 |
|
Lhermitte R M. 1966. Probing air motion by doppler analysis of Radar clear air returns[J]. Journal of the Atmospheric Sciences, 23(5): 575–591.
DOI:10.1175/1520-0469(1966)023<0575:PAMBDA>2.0.CO;2 |
|
Petitdidier M, Sy A, Garrouste A, et al. 1997. Statistical characteristics of the noise power spectral density in UHF and VHF wind profilers[J]. Radio Science, 32(3): 1229–1247.
DOI:10.1029/97RS00250 |
|
Rogers R R. 1964. An extension of the Z-R relation for Doppler radars[C]. The 11th Weather Radar Conference AMS, Boston, MA., Goulder, Co., Sept., 14-18.
|
|
Shupe M D, Kollias P, Poellot M, et al. 2008. On deriving vertical air motions from cloud Radar Doppler spectra[J]. Journal of Atmospheric & Oceanic Technology, 25(4): 547.
|
|
Testud J, Oury S, Black R A, et al. 2001. The concept of 'normalized' distribution to describe raindrop spectra:A tool for cloud physics and cloud remote sensing[J]. Journal of Applied Meteorology, 40(40): 1118–1140.
|
|
Ulbrich C W. 1983. Natural Variations in the analytical form of the raindrop size distribution[J]. J Climate and Applies Meteorology, 22(10): 1764–1775.
DOI:10.1175/1520-0450(1983)022<1764:NVITAF>2.0.CO;2 |
|
Yahao W U, Liu L. 2017. Statistical characteristics of raindrop size distribution in the Tibetan Plateau and Southern China[J]. Advances in Atmospheric Sciences, 34(6): 727–736.
DOI:10.1007/s00376-016-5235-7 |
|
Zheng J F, Liu L P, Zhu K Y, et al. 2017. A method for retrieving vertical air velocities in convective clouds over the Tibetan Plateau from TIPEX-Ⅲ Cloud Radar DopplerSpectra[J]. Remote Sensing, 9(9): 964.
DOI:10.3390/rs9090964 |
|
樊雅文. 2012.云雷达资料订正及应用研究[D].南京: 南京信息工程大学.
|
|
刘黎平, 谢蕾, 崔哲虎. 2014. 毫米波云雷达功率谱密度数据的检验和在弱降水滴谱反演中的应用研究[J]. 大气科学, 38(2): 223–236.
DOI:10.3969/j.issn.1674-7097.2014.02.011 |
|
刘黎平, 周淼. 2016. 垂直指向的Ka波段云雷达观测的0℃层亮带自动识别及亮带的特征分析[J]. 高原气象, 35(3): 734–744.
DOI:10.7522/j.issn.1000-0534.2014.00160 |
|
彭亮, 陈洪滨, 李柏. 2012. 3 mm多普勒云雷达测量反演云内空气垂直速度的研究[J]. 大气科学, 36(1): 1–10.
|
|
阮悦, 阮征, 魏鸣, 等. 2018. 基于C-FMCW雷达的高原夏季对流云垂直结构分析研究[J]. 高原气象, 37(1): 93–105.
DOI:10.7522/j.issn.1000-0534.2017.00025 |
|
孙豪, 刘黎平. 2017. 不同波段垂直探测雷达对降水云雨滴谱反演效果对比分析[J]. 成都信息工程大学学报, 32(1): 35–40.
|
|
王洪, 雷恒池, 杨洁帆. 2017. 微降水雷达测量精度分析[J]. 气候与环境研究, 22(4): 392–404.
|
|
温龙, 刘溯, 赵坤, 等. 2015. 两次降水过程的微降雨雷达探测精度分析[J]. 气象, 41(5): 577–587.
|
|
谢蕾, 刘黎平, 姚雯. 2014. 毫米波雷达与雨滴谱仪观测弱降水的对比分析[J]. 成都信息工程学院学报, 29(1): 39–46.
DOI:10.3969/j.issn.1671-1742.2014.01.007 |
|
吴亚昊, 刘黎平, 周筠珺, 等. 2016. 雨滴谱的变化对降水估测的影响研究[J]. 高原气象, 35(1): 220–230.
DOI:10.7522/j.issn.1000-0534.2014.00093 |
|
姚志刚, 杨超, 赵增亮, 等. 2018. 毫米波雷达反演层状云液态水路径研究[J]. 高原气象, 37(1): 223–233.
DOI:10.7522/j.issn.1000-0534.2016.00127 |
|
郑佳锋, 刘黎平, 刘艳霞, 等. 2016a. 云雷达回波强度谱密度定标及云内大气垂直运动速度反演试验[J]. 高原气象, 35(6): 1650–1661.
DOI:10.7522/j.issn.1000-0534.2015.00064 |
|
郑佳锋, 刘黎平, 曾正茂, 等. 2016b. Ka波段毫米波云雷达数据质量控制方法[J]. 红外与毫米波学报, 35(6): 748–757.
|
|
郑娇恒, 陈宝君. 2007. 雨滴谱分布函数的选择:M-P和Gamma分布的对比研究[J]. 气象科学, 27(1): 17–25.
DOI:10.3969/j.issn.1009-0827.2007.01.003 |
2. Plateau Atmosphere and Environment Key Laboratory of Sichuan Province, Chengdu University of Information Technology, Chengdu 610025, Sichuan, China
 2019, Vol. 38
2019, Vol. 38
