2. 城市水循环与海绵城市技术北京市重点实验室, 北京 100875
降水作为水循环中的重要一环, 对能量和物质的交换起着十分关键的作用, 具有十分重要的气候学和水文学意义。降水在时空分布上差别较大, 降水量的多少可以对区域性气候形成影响, 开展区域性降水分析, 对区域水资源的合理利用, 灾害的预防具有十分重要的现实意义。地面站点是降水数据最直接的来源, 可以提供较完整的观测结果, 但站点数据代表性有限, 无法真实反映较大区域内降水的分布特征、变化规律, 尤其在青藏高原西部地区, 海拔较高、交通不便, 气候条件复杂多变, 站点布设稀少, 且站点主要集中在低海拔地区, 空间分布不均匀。所以仅通过地面气象站点获得的降水数据的空间分辨率较差, 在整个流域上降水资料代表性不足, 且容易受到区域气候影响, 数据的精确性也不足。降水卫星具有实时观测, 不受地理条件限制等优点, 可以获取地面站点稀少地区的降水资料, 从而弥补地面气象站点对降水数据时空观测不足的缺点。近年来降水卫星数据在暴雨分析、干旱演变、水文模拟等领域得到了广泛应用(张立生等, 2007; 杜灵通等, 2012; 曾昭昭等, 2017; 刘建军等, 2017), 但是由于降水卫星在数据影像获取、传输、反演计算的过程中均存在一定的误差, 因此卫星降水数据存在一定的不确定性(Hong et al, 2006), 在使用降水卫星数据对区域水资源评价前, 需要对数据的精度进行评估, 以便验证降水卫星资料在无资料和地势复杂地区的适用性。
国内外学者对多种降水卫星产品进行了数据精度评估相关工作, 例如廖荣伟等(2015)在整个中国范围内, 将6种降水卫星数据与地面站点的数据进行对比分析, 得出在中国春、夏、秋季的卫星数据精度大于冬季降水数据精度, 整体上CMORPH (CPC MORPHing technique)数据对降水的刻画能力比较好的结论。张蒙等(2016)在青藏高原地区对五种降水卫星数据的反演能力进行了评估, 发现五种降水卫星数据在夏季的反演能力高于冬季反演能力, 白天的精度高于夜晚的精度, 并且降水卫星数据对大雨和暴雨的反演能力偏弱。吕洋等(2013), 齐文文等(2013), 江善虎等(2014)及李蒙等(2017)评价了TRMM卫星数据在不同流域的反演精度, 时空分布以及对水文模型驱动的效果, 认为TRMM降水卫星数据在日尺度上对降水的反演能力较弱, 月尺度上对降水的反演能力较强, 用TRMM数据模拟的月尺度径流过程与实际径流吻合较好。许时光等(2014, 2015)对CMORPH卫星数据在区域上的误差特征进行了分析, 并对CMORPH数据进行了修正, 经过修订后的CMORPH数据年均方根误差明显减少, 相关系数在不同程度上有所提高, 青藏高原地区的降水模拟精度得到了有效的提高。计晓龙等(2017)利用CMORPH数据对青藏高原夏季降水日变化进行了研究, 认为青藏高原地区夏季降水量和降水频率的日变化呈明显的双峰结构, 而降水强度的双峰结构不明显。Smith et al(2006)利用GPCP卫星降水数据, 就卫星降水评价中如何减少系统误差进行了探讨。Alijanian et al(2017)选用PERSIANN、TRMM、PERSIANN-CDR、MSWEP、CMORPH五种降水卫星数据分别在日、月、季的时间尺度和气候区空间尺度上对降水卫星的精度进行了评价。
雅鲁藏布江流域位于中国西南部的高寒地区, 地形复杂、气候多变, 气象站点布设稀少, 空间分布极度不均。目前, 在雅鲁藏布江流域降水卫星数据的精度评价工作开展的相对较少(吕洋等, 2013; 黄浠等, 2016), 研究也多利用定量指标进行, 不能很好的反映卫星数据对降水事件尤其是降水量的反演能力。因此, 本文研究针对雅鲁藏布江流域的降水卫星数据精度评价开展相关工作。本研究首先选取多种定量指标和分类指标构建降水卫星数据精度评价体系, 评价了雅鲁藏布江流域1998—2015年PERSIANN-CDR(简称PERSIANN)、TRMM 3B42 V7(简称TRMM)卫星降水数据精度, 并分析两种降水卫星数据在雅鲁藏布江流域的时空分布规律以及差别的原因; 然后, 基于评价结果, 第一次在雅鲁藏布江流域采用降水量分类指标, 作为PERSIANN和TRMM降水卫星数据的评价体系的补充指标, 有效地区分出降水卫星数据对地面降水特征的捕捉能力的差别。本研究可以为其他无资料、缺资料高寒地区降水卫星数据精度验证提供范例, 并为进一步利用降水卫星数据进行水文计算、气候数值模拟提供参考依据。
2 研究区概况与资料选取 2.1 研究区概况雅鲁藏布江流域位于青藏高原东南部地区(图 1), 在26°N—39.8°N, 73.5°E—104.7°E之间。流域的平均海拔为4000 m, 是世界上海拔最高的高原河流, 其支流众多, 水资源十分充沛, 是我国西藏地区淡水资源的主要来源之一, 同时也是下游其他国家用水的主要水源之一(刘天仇, 1999)。雅鲁藏布江流域属于多气候交织带, 上游地区(杰马央宗冰川末端-里孜)是典型的高寒温带半干旱气候, 中游地区(里孜-派镇)是高原温带半干旱气候, 下游地区(派镇-巴昔)是热带亚热带季风气候(杨志刚等, 2014)。流域的年平均降水量为428.7 mm, 受到气候和地形的综合影响, 雅鲁藏布江流域内降水分布极不均匀, 流域的东南部地区年降水量充沛, 西北地区降水稀少, 空间变异性较大。
|
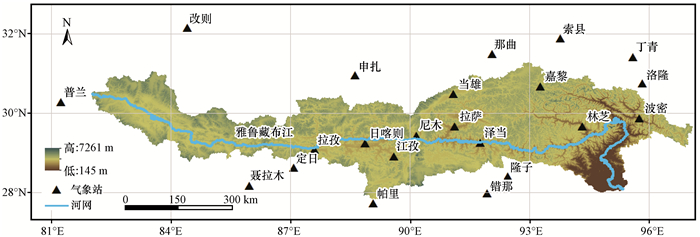
图 1 雅鲁藏布江流域位置及气象站点分布 Fig. 1 The distribution of meteorological stations in the Yarlung Zangbo River basin |
使用的站点降水数据时间范围为1998—2015年, 采用日数据进行分析。数据来源于中国国家气象数据中心, 通过了均一性检验以及质量控制(江志红等, 2008), 说明气象站点的数据质量较好, 可以用于雅鲁藏布江流域降水卫星数据精度评价。雅江流域内仅只有11个气象站点, 且主要集中在流域的中部地区, 在西部地区布设点稀少, 数据的空间连续性相对比较差, 为了全面的反映出流域的降水情况, 选用流域内外22个气象站点作为降水卫星数据精度验证的观测站点(图 1), 其值为实测值。
采用TRMM 3B42 V7(Kummerow et al, 1998; 唐国强等, 2015)和PERSIANN-CDR(Sorooshian et al, 2000; Hong et al, 2004)两种降水卫星数据, 其数据来源及分辨率等详细信息如表 1所示。
| 表 1 气象卫星的时空分辨率和可用数据时间段 Table 1 Characteristics of the two satellite products |
为了全面反映降水卫星数据产品在雅鲁藏布江流域的精度特征, 本研究采用定量指标和分类指标对卫星数据精度进行评价, 其中, 定量指标可以反映卫星降水数据与地面站点的数据在数量上的一致, 而分类指标可以反映降水卫星数据对降水事件发生可能性的捕捉能力(廖荣伟等, 2015)。为了进一步阐释降水卫星数据对降水量的捕捉能力, 在定量和分类指标的基础上, 采用降水量体积分类指标(Sorooshian et al, 2000), 作为评价体系的补充指标, 对降水卫星反演降水事件中降水量的精度进行评估。由于降水卫星数据与地面站点位置处的数据不一定匹配, 采用双线性插值的方法得到地面站点位置处的卫星数据。为了显示各站点的定量指标以及分类指标在流域的空间分布, 采用反距离加权平均的方法, 求得各指标在流域上的空间分布(Hu et al, 2014)。
3.1 降水评估定量指标定量指标可以从整体上把握降水卫星数据的精度, 用以判断降水卫星数据的可靠性。选择偏差Bias和相关系数Corr两种定量指标(Hu et al, 2014; 孙乐强等, 2014)对雅鲁藏布江地区的卫星数据与站点数据之间的相关性和误差分析, 评价卫星数据与实测数据在数量上的精度, 具体计算方法如下:
(1) 偏差(Bias)
偏差Bias在本研究中表示降水卫星数据与地面站点的数据之间的偏离大小。
| $ Bias=\frac{\sum\limits_{i=1}^{n}\left(S I M_{i}-O B S_{i}\right)}{\sum\limits_{i=1}^{n} O B S_{i}}, $ | (1) |
式中: n为降水日数; OBS为地面站点的观测降水量(单位: mm); SIM为与地面站点位置相同的卫星反演的降水量(单位: mm)。Bias为正, 表示降水卫星数据比站点观测数据大, 即卫星数据高估了降水量。Bias为负, 表示降水卫星数据比站点数据小, 即卫星数据低估了降水量。Bias愈接近于0, 则降水卫星数据与地面站点的数据之间的差别愈小, 降水卫星数据的精度愈高。
(2) 相关系数(Corr)
相关系数Corr反映了降水卫星数据与地面站点的数据之间的线性相关程度。
| $ Corr=\frac{\sum\limits_{i=1}^{n}\left(S M_{i}-\overline{S I M}\right)\left(O B S_{i}-\overline{O B S}\right)}{\sqrt{\sum\limits_{i=1}^{n}\left(S M_{i}-\overline{S M}\right)^{2} \cdot \sum\limits_{i=1}^{n}\left(O B S_{i}-\overline{O B S}\right)^{2}}}, $ | (2) |
式中: OBS为地面站点观测到的降水量的平均值(单位: mm); SIM为卫星反演的降水量的平均值(单位: mm)。相关系数的范围为-1~1, 相关系数大于0, 表示卫星数据与地面站点的数据之间是正相关, 相关系数小于0, 表示卫星数据与地面站点的数据之间是负相关, 其绝对值愈接近于1, 说明降水卫星数据和地面站点的数据之间的相关性愈好。
3.2 降水评估分类指标由于降水数据的收集和观测具有非连续性, 一次降水事件存在发生或不发生的情况, 因此, 在利用定量指标对降水数量进行评价的基础上, 还需利用降水卫星捕捉到的降水事件和地面站点观测降水事件是否一致的分类指标, 对卫星反演降水事件的能力进行评价。分类指标可以评价卫星对降水事件和无降水事件捕捉的能力, 可以由降水事件的列联表定义(表 2)(Aghakouchak et al, 2013)。
| 表 2 地面降水事件和卫星捕捉降水事件发生情况表 Table 2 The contingency table for satellite products |
(1) 探照率(POD)
POD(Probability of Detection)是指降水卫星能正确的探测到的降水事件的次数在所有降水事件次数中的比例。
| $ P O D=\frac{\text { hit }\_ \text { num }}{\text { hit }_{\text { - }} \text { num }+\text { miss }\_ \text { num }}, $ | (3) |
式中: hit_num为地面站点探测到降水事件的情况下, 降水卫星也探测到该次降水事件的次数; miss_num为地面站点探测到降水事件, 降水卫星未探测到此次降水事件所漏报的次数。POD的数值范围为0~1, 其值愈接近于1, 表示卫星对降水事件探测能力愈高。
(2) 错报率(FAR)
FAR(False Alarm Ration)是指卫星误将无降水事件识别为降水事件的次数在卫星观测到降水事件总数中的比例, 表示卫星对降水事件报错的概率。
| $ F A R=\frac{\text { false }\_ \text { num }}{\text { false }\_ \text { num }+\text { hit }\_ \text { num }}, $ | (4) |
式中: false_num为在地面站点未探测到降水事件发生的情况下, 降水卫星误探测到此次降水事件的次数。FAR的数值范围为0~1, 其数值愈接近于0, 则卫星错报的降水事件愈少, 说明降水卫星对降水事件错报的几率愈小。
3.3 降水量体积分类指标为进一步说明降水量对不同卫星产品的影响, 定义降水量分类指标(Aghakouchak et al, 2013), 作为定量和分类指标评价体系的补充指标, 并首次在雅鲁藏布江流域进行应用。分别定义降水量探照率VHI、降水量错报率VFAR、降水量漏报率VMI三个指标。
(1) 降水量探照率(Volumetric Hit Index, VHI)
| $ \mathit{VHI}{\rm{ = }}\frac{{\sum\limits_{i = 1}^n {\left[ {{\rm{SI}}{{\rm{M}}_i}|\left({{\rm{SI}}{{\rm{M}}_i} > {\rm{thr\& OB}}{{\rm{S}}_i} > {\rm{thr}}} \right)} \right]} }}{{\sum\limits_{i = 1}^n {\left[ {{\rm{SI}}{{\rm{M}}_i}|\left({{\rm{SI}}{{\rm{M}}_i} > {\rm{thr\& OB}}{{\rm{S}}_i} > {\rm{thr}}} \right)} \right]} + \sum\limits_{i = 1}^n {\left[ {{\rm{OB}}{{\rm{S}}_i}|\left({{\rm{SI}}{{\rm{M}}_i} \le {\rm{thr\& OB}}{{\rm{S}}_i} > {\rm{thr}}} \right)} \right]} }}, $ | (5) |
式中: n为降水日数; thr为降水量阈值, 不同的thr下分类指标大小可以反映降水卫星对不同降水类型的降水反演精度。本研究探讨降水卫星对降水发生与否的捕捉性能, 所以阈值设置为0 mm·d-1(有无降水事件发生的临界值), 其他各变量的含义同公式(1)。VHI是指标POD的拓展, 表示在阈值thr以上的降水量能够被正确侦测到的比例, 它的数值范围为0~1, 其值愈接近于1, 表示卫星能够正确侦测到的降水量愈多。
(2) 降水量错报率(Volumetric False Alarm Ratio, VFAR)
| $ \mathit{VFAR}{\rm{ = }}\frac{{\sum\limits_{i = 1}^n {\left[ {{\rm{SI}}{{\rm{M}}_i}|\left({{\rm{SI}}{{\rm{M}}_i} > {\rm{thr\& OB}}{{\rm{S}}_i} \le {\rm{thr}}} \right)} \right]} }}{{\sum\limits_{i = 1}^n {\left[ {{\rm{SI}}{{\rm{M}}_i}|\left({{\rm{SI}}{{\rm{M}}_i} > {\rm{thr\& OB}}{{\rm{S}}_i} > {\rm{thr}}} \right)} \right]} + \sum\limits_{i = 1}^n {\left[ {{\rm{OB}}{{\rm{S}}_i}|\left({{\rm{SI}}{{\rm{M}}_i} > {\rm{thr\& OB}}{{\rm{S}}_i} \le {\rm{thr}}} \right)} \right]} }}, $ | (6) |
VFAR是指标FAR的拓展, 表示在阈值thr以上的降水量被卫星误判的比例, 它的数值范围为0~1, 其值愈接近于0, 表示降水量被卫星误判的可能愈小。
(3) 降水量漏报率(Volumetric Miss Index, VMI)
| $\mathit{VMI}{\rm{ = }}\frac{{\sum\limits_{i = 1}^n {\left[ {{\rm{OB}}{{\rm{S}}_i}|\left({{\rm{SI}}{{\rm{M}}_i} > {\rm{thr\& OB}}{{\rm{S}}_i} > {\rm{thr}}} \right)} \right]} }}{{\sum\limits_{i = 1}^n {\left[ {{\rm{SI}}{{\rm{M}}_i}|\left({{\rm{SI}}{{\rm{M}}_i} > {\rm{thr\& OB}}{{\rm{S}}_i} > {\rm{thr}}} \right)} \right]} + \sum\limits_{i = 1}^n {\left[ {{\rm{OB}}{{\rm{S}}_i}|\left({{\rm{SI}}{{\rm{M}}_i} \le {\rm{thr\& OB}}{{\rm{S}}_i} > {\rm{thr}}} \right)} \right]} }}, $ | (7) |
VMI表示在阈值thr以上的降水量被卫星漏报的比例, 它的数值范围为0~1, 其值愈接近于0, 表示降水量被卫星漏报的可能愈小。
4 结果与分析 4.1 不同降水区间内卫星数据与站点数据偏差分析微量降水和重度降水是中高纬度地区降水的重要组成部分, 它们的次数和数量在流域降水事件中占了相当大的比例, 评价卫星对这两类极端降水类型的捕捉能力, 对分析雅鲁藏布江流域降水规律和时空分布具有十分重要的意义。本文计算1998—2015年不同降水量范围内的降水卫星数据和地面站点的数据在整个流域平均偏差Bias(图 2)。
|
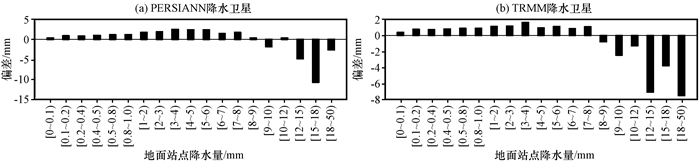
图 2 不同降水量范围内的降水卫星数据和地面站点的数据之间的平均偏差分布 Fig. 2 Distribution of mean bias between satellite data and stations data for different precipitation ranges |
从图 2中可以看出, PERSIANN卫星数据在0~0.5 mm日降水量范围内的偏差占了正偏差的15%, TRMM卫星数据在0~0.5 mm日降水量范围的偏差占了正偏差(偏差值为正的部分, 即平均偏差分布图中横坐标以上的部分)的22%。PERSIANN卫星数据在9~50 mm日降水量范围内的偏差占了总偏差(所有的偏差值之和, 即平均偏差分布图中坐标轴以上和以下部分之和)大小的54%, TRMM卫星数据在9~50 mm日降水量范围内的偏差占了总偏差大小的44.7%, 说明微量和重度降水偏差是造成降水卫星数据偏差的主要原因。两种降水卫星数据与地面站点的数据的偏差分布整体呈现类似规律, 但在不同的降水范围内偏差不同。在降水量比较小的范围内, 两种降水卫星数据偏差均为正值, 即它们在不同程度上高估小降水量。在降水量相对较大的范围内, 两种降水卫星数据的偏差均为负值, 即它们低估大降水量, 整体上, 降水量范围越大, 卫星降水数据与地面站点的数据之间的偏差越大。TRMM降水卫星数据在大降水量上的偏差要大于PERSIANN数据在大降水量上的偏差。总体而言, 两种降水卫星数据均在不同程度上对降水的估计有偏差, 降水卫星数据总是高估了小降水量, 低估了大降水量, 但是PERSIANN降水卫星要比TRMM降水卫星对降水数据偏离程度小。
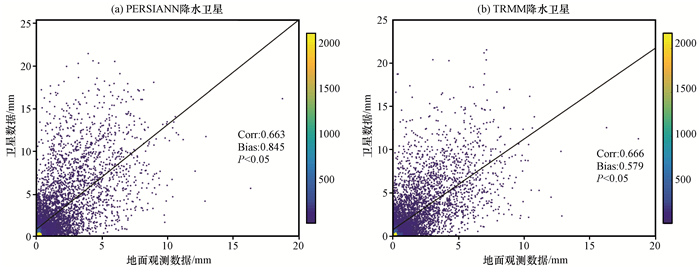
4.2 卫星降水数据与站点降水数据定量分析 4.2.1 卫星降水数据精度评估为评估降水卫星数据在雅鲁藏布江流域的适用性, 检验卫星降水数据的精度, 计算了卫星降水数据与地面站点的数据之间的相关系数Corr、相对误差Bias、平均误差ME, 均方根误差RMSE(图 3)。图 3中直线表示卫星数据和散点数据拟合的直线, 不同的颜色表示散点出现的数量多少, 即降水卫星反演的降水量的密集程度, 从图 3中可以看出, PERSIANN和TRMM降水卫星产品对雅鲁藏布江流域反演的日降水量数值均集中在0~0.43 mm, 均以小降水事件为主, 分别占到全部降水事件的32%和34%。从两个卫星的定量指标上看, PERSIANN降水卫星数据的相关系数平均值为0.663, Bias的平均值为0.845。TRMM降水卫星数据的相关系数平均值为0.666, Bias的平均值为0.579。TRMM降水卫星数据的相关系数只比PESIANN降水卫星数据的相关系数高出了0.45%。两个卫星的相关系数差别不大, 精度相近, PERSIANN和TRMM卫星数据在整体上都能够很好地反演出地面的整体降水情况。
|
图 3 1998—2015年PERSIANN卫星和TRMM卫星降水数据与地面站点数据密度散点分布 P<0.05表示通过95%信度水平检验 Fig. 3 Precipitation scatter density diagram between satellite data and stations data in the Yarlung Zangbo River basin during 1998—2015 |
气象观测站点受到海拔、地形、空间分布的综合影响, 每个站点的精度都会有不同的差异。为更好地评估单个站点的精度, 计算了雅鲁藏布江流域内22个站点的降水卫星数据与地面观测数据之间的相关系数和偏差(表 3)。从表 3中可以看出, 各地面站点观测数据与降水卫星数据之间的相关系数集中在0.21~0.4, 在各个站点中, 相关系数的最大值出现在PERSIANN卫星数据反演的日喀则站, 只有0.428, 并通过了95%的信度水平检验(p<0.05)。降水卫星数据在日尺度上各站点之间的相关系数比流域整体的相关系数明显降低, 其精度效果不太理想, 一方面是因为计算雅鲁藏布江流域整体的相关系数时, 掩盖住了个别站点卫星降水数据与站点数据之间的差异性, 无法明确反映出各个站点之间相关系数的不同。另一方面, 下垫面干扰了卫星对降水的反演能力, 使得各站点之间的相关系数比较小。如积雪和高山陆地覆盖的冰面会对卫星反演降水产生影响(Levizzani et al, 2011), 并且在高海拔的山区, 流域上空常年存在云层, 云顶上空产生的红外辐射影响也会对降水卫星的精度产生一定的影响(Dinku et al, 2007)。
| 表 3 雅鲁藏布江流域1998—2015年PERSIANN、TRMM数据与地面站点的数据的相关系数和偏差 Table 3 Coefficient of correlation and deviation of the two satellite products in the Yarlung Zangbo River basin |
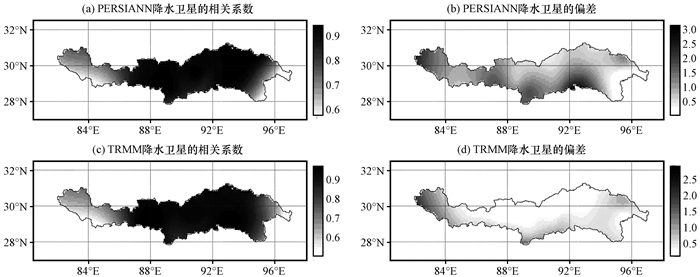
两种降水卫星数据的相关系数在整体上的空间分布相似(图 4), 均在流域的中游位置处相关系数比较大, 上游和下游位置的相关系数比较小。相关系数在流域上游位置比较小的原因, 可能是雅鲁藏布江流域西部地区是喀刺昆仑山脉, 深居高原西北地区, 温暖湿润的气团难以到达, 降水量极少, 卫星数据与地面站点的数据的相关性比较差。相关系数在流域的下游东南地区位置比较小的原因, 一方面是该地区气象站点比较稀疏, 尤其是流域的出口位置, 属于气象站点的空白区, 通过插值得到流域的空间分布图时, 受到无站点分布的影响, 该处的相关系数就会整体偏小。另一方面可能是因为卫星对微量降水和重度降水类型的反演能力比较差, 所以在下游地区相关系数也相对较差(两种降水卫星数据总是高估小降水量, 低估大降水量)。对于单个卫星而言, PERSIANN降水卫星数据与地面站点数据相关系数的范围为0.208~0.482, TRMM降水卫星数据与地面站点数据相关系数的范围为0.166~0.44。在相关系数数值上, PERSIANN卫星数据与地面站点之间的相关系数要略大于TRMM数据与地面站点之间的相关系数。
|
图 4 雅鲁藏布江流域1998—2015年卫星数据与地面站点数据的相关系数(左)和偏差(右)空间分布 Fig. 4 Distribution of correlation coefficient (left) and bias (right) between satellite data and stations data in the Yarlung Zangbo River basin during 1998—2015 |
降水卫星数据与地面站点数据的偏差Bias在整体上的空间分布规律(图 4)可以看出, Bias的空间分布图呈现与Corr的空间布局相似的规律, 均为在流域的上游和中游地区, 偏差相对比较大, 在下游地区偏差相对比较小。对于单个站点而言, PERSIANN卫星数据与地面站点的数据的偏差范围为-0.216~1.601, TRMM卫星数据与地面站点的数据的偏差的范围为-0.375~1.194, PERSIANN和TRMM降水卫星在流域的各站点上均有不同程度的高估降水量情况, 但相比于TRMM卫星数据, PERSIANN数据的高估的量相对较小。在雅鲁藏布江流域的西南部和中南部地区偏差比较大, 而在东南部地区的偏差相对比较小。从整个青藏高原水汽输送和降水的关系上分析, 这可能是由于喜马拉雅山脉的阻挡, 自孟加拉湾来的暖湿气流无法越过重重山脉, 在雅鲁藏布江和喜马拉山脉之间形成一个少雨地带(齐文文等, 2013; 林厚博等, 2016; 谢欣汝等, 2018), 夹带中降水量相对偏少, 所以在雅鲁藏布江流域中南和西南地区的偏差相对较大。
综上所述, PERSIANN卫星数据和TRMM卫星数据的相关系数和偏差数值相近, 空间分布相似, PERSIANN和TRMM降水卫星数据均能够反映出地面降水的情况。仅从定量指标上看, 两个卫星对地面降水反演结果的差别较小, 精度相似。
4.3 卫星降水数据与站点降水数据分类指标比较分析定量指标无法反映出降水卫星对一次特定降水事件发生与否的捕捉能力(如地面站点观测到一次降水事件, 降水卫星是否能够捕捉到这次事件, 以及捕捉的降水量是多少)。因此, 在定量指标评价的基础上, 进一步选取分类指标和降水量分类指标对卫星数据的捕捉精度进行分析。在雅鲁藏布江流域应用降水量分类指标, 是对高寒地区无资料、缺资料地区卫星降水精度评估的有益尝试, 可以在常用分类指标的基础上提供额外的降水量信息。对未来雅鲁藏布江流域气候数值模拟分析等提供借鉴。
4.3.1 卫星降水数据整体精度检验从1998—2015年雅鲁藏布江流域站点的分类指标(图 5)中可以看出, 指标数值(或者1-指标数值)越大表明卫星对降水事件或降水量的反演精度越高。
|
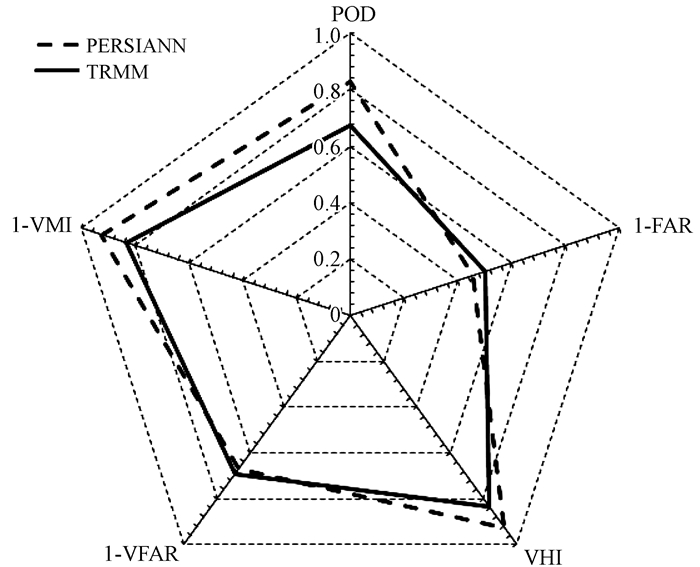
图 5 PERSIANN和TRMM降水卫星分类指标 Fig. 5 Indices in detecting precipitation between PERSIANN and TRMM |
POD表示降水卫星能正确探测到的降水事件的次数在所有降水事件次数中的比例, PERSIANN卫星的POD值为0.830, TRMM卫星的POD值为0.674。PERSIANN卫星比TRMM卫星的POD高了23.1%, 说明PERSIANN降水卫星能够捕捉到雅鲁藏布江流域发生的绝大部分降水事件, 而TRMM降水卫星遗漏了相当一部分降水事件。
VHI数值大小反映流域的降水事件中有多少降水量可以被卫星正确探测到的比例, PERSIANN降水卫星的VHI为0.927, TRMM卫星的VHI为0.833, 说明PERSIANN降水卫星捕捉降水量的能力同样比TRMM卫星捕捉降水量的能力强。
FAR反映了卫星将无降水事件识别为降水事件的次数在卫星观测到降水事件总数中的比例。PERSIANN和TRMM卫星的FAR值分别为0.54和0.50。VFAR数值大小反映流域的降水事件中有多少降水量可以被卫星错误判断的比例, PERSIANN降水卫星的VFAR值为0.33, 而TRMM降水卫星的VFAR为0.31, 两个卫星对降水量的“误判”情况类似。PERSIANN降水卫星在减少误报降水事件的能力上略差于TRMM, 但是差别不大。这可能与TRMM卫星搭载了TMI(微波成像仪)、测雨雷达PR等传感器有关(Kummerow et al, 1998)。VMI数值大小反映流域的降水事件中有多少降水量可以被卫星漏掉的比例, PERSIANN和TRMM卫星的VMI值分别为0.073和0.167。PERSIANN卫星能够捕捉更多的降水量, 被其“漏掉”的降水量更少。
在流域整体上, 雷达图包围的面积越大表示降水卫星对降水的反演能力越强, PERSIANN降水卫星在雷达图中包围的面积要高于TRMM所包围的面积, 表明PERSIANN降水卫星对降水事件和降水量的反演精度要高于TRMM降水卫星。
4.3.2 卫星降水数据站点精度检验从POD、VHI、FAR、VFAR、VMI五种分类指标在流域上的空间分布(图 6)中可以看出, PERSIANN降水卫星的POD值范围是0.664~0.902, 在空间分布上存在从东南向西北逐渐增加的趋势, 越接近流域出口位置, 卫星的POD值越小, 表明在流域的下游地区, PERSIANN卫星对降水事件的探测能力低于其他地区。TRMM降水卫星的POD值范围是0.488~0.743, 在空间分布上相对比较均匀, 在流域的中下游位置处形成一个POD较大的高值区。但是PRESIANN降水卫星的取值范围整体上要高于TRMM, 所以在空间分布上, PERSIANN对降水的探测能力要高于TRMM卫星。两个降水卫星的VHI空间分布与POD分布相似, 但是PERSIANN降水卫星的VHI值要略大于TRMM降水卫星, 即PERSIANN在整个空间流域上对降水量的捕捉能力高于TRMM卫星。两个降水卫星的VFAR空间分布相似, 均在流域的西北部地区偏大。两个降水卫星的VMI空间分布与POD存在此消彼长的趋势, 呈现出“跷跷板”分布状态, 因为卫星对降水事件捕捉的越多, 漏报的可能性越小, 但是在22个站点中PERSIANN卫星的VMI的值整体偏小。

|
图 6 降水卫星分类指标数值在雅鲁藏布江流域空间分布 Fig. 6 Distribution of indices in detecting precipitation in the Yarlung Zangbo River basin |
综上, 在空间分布上, PERSIANN卫星在各站点上的POD和VHI指标都要大于TRMM在各站点上的POD和VHI指标, 表明PERSIANN降水卫星对降水事件和降水量的捕捉和侦探能力比TRMM降水卫星对降水事件和降水量的捕捉和探测能力强。
5 结论以雅鲁藏布江流域作为研究区, 基于国家气象中心的地面站点观测数据, 选取多种定量指标和分类指标构建降水卫星数据精度评价指标体系, 在日尺度上对PERSIANN-CDR和TRMM 3B42 V7卫星降水数据的反演能力进行了评估, 并分析其在雅鲁藏布江流域的适用性。此外, 首次在雅鲁藏布江流域采用降水量分类指标, 作为PERSIANN和TRMM降水卫星数据评价指标体系的补充指标, 相比于仅考虑传统定量指标, 使用分类指标和降水量分类指标, 能够更加有效地区分降水卫星对降水的反演精度差别。得到以下主要结论:
(1) PERSIANN卫星数据和TRMM卫星数据精度存在降水类型不稳定性, 并随着降水量范围的增大而增大。日降水量范围在0~0.5 mm的降水类型中, 两个卫星数据存在明显的高估, PERSIANN卫星数据的偏差在正偏差中占了15%, TRMM卫星数据在正偏差中占了22%。日降水量在9~50 mm的降水范围内, PERSIANN卫星数据的偏差占了总偏差大小的54%, TRMM卫星数据的偏差占了总偏差大小的44.7%。两种降水卫星均在不同程度上对降水的估计有偏差, 总是高估了小降水量, 低估了大降水量, 并且PERSIANN降水卫星数据要比TRMM降水卫星对降水数据偏离程度小。
(2) PERSIANN降水卫星数据的相关系数平均值为0.663, Bias的平均值为0.845。TRMM降水卫星数据的相关系数平均值为0.666, Bias的平均值为0.579。仅从定量指标上看, 两个卫星数据的相关系数差别较小, 精度接近。
(3) 基于分类指标和降水量分类指标的评价指标体系, 可以更加有效的区分PERSIANN卫星和TRMM卫星对降水的反演能力。整体上, PERSIANN卫星的POD值为0.830, VHI为0.927, FAR值为0.54, VFAR值为0.33, VMI值为0.073。TRMM卫星的POD值为0.674, VHI为0.833, FAR值为0.50, VFAR值为0.31, VMI值为0.167。在空间分布上, PERSIANN卫星在各站点的各分类指标优于TRMM卫星的指标。考虑降水量分类指标的评价指标体系比单纯使用传统定量指标评价降水卫星的精度能更加有效地反映出降水卫星对地面降水特征的捕捉能力大小, PERSIANN卫星对降水事件和降水量的反演精度要高于TRMM卫星。
Aghakouchak A, Mehran A. 2013. Extended contingency table:Performance metrics for satellite observations and climate model simulations[J]. Water Resources Research, 49(10): 7144–7149.
DOI:10.1002/wrcr.20498,2013 |
|
Alijanian M, Rakhshandehroo G R, Mishra A K, et al. 2017. Evaluation of satellite rainfall climatology using CMORPH, PERSIANN-CDR, PERSIANN, TRMM, MSWEP over Iran[J]. International Journal of Climatology, 37(14): 4896–4914.
DOI:10.1002/joc.5131 |
|
Dinku T, Ceccato P, Lemma M, et al. 2007. Validation of satellite rainfall products over East Africa's complex topography[J]. International Journal of Remote Sensing, 28(7): 1503–1526.
DOI:10.1080/01431160600954688 |
|
Hong Y. 2004. Precipitation estimation from remotely sensed information using Artificial Neural Network-Cloud Classification System[J]. Journal of Applied Meteorology, 36(9): 1176–1190.
DOI:10.1175/1520-0450(1997)036 |
|
Hong Y, Hsu K L, Moradkhani H, et al. 2006. Uncertainty quantification of satellite precipitation estimation and Monte Carlo assessment of the error propagation into hydrologic response[J]. Water Resources Research, 42(8): 2643–2645.
DOI:10.1029/2005WR004398,2006 |
|
Hu Q, Yang D, Li Z, et al. 2014. Multi-scale evaluation of six high-resolution satellite monthly rainfall estimates over a humid region in China with dense rain gauges[J]. International Journal of Remote Sensing, 35(4): 1272–1294.
DOI:10.1175/JAM2173.1 |
|
Kummerow C, Barnes W, Kozu T, et al. 1998. The Tropical Rainfall Measuring Mission (TRMM) sensor package[J]. Journal of atmospheric and oceanic technology, 15(3): 809–817.
DOI:10.1175/1520-0426(1998)015 |
|
Levizzani V, Laviola S, Cattani E. 2011. Detection and measurement of snowfall from space[J]. Remote Sensing, 3(1): 145–166.
DOI:10.3390/rs3010145 |
|
Smith T M, Arkin P A, Bates J J, et al. 2006. Estimating bias of satellite-based precipitation estimates[J]. Journal of Hydrometeorology, 7(5): 841–856.
DOI:10.1175/JHM524.1 |
|
Sorooshian S, Hsu K L, Gao X, et al. 2000. Evaluation of PERSIANN system satellite-based estimates of tropical rainfall[J]. Bulletin of the American Meteorological Society, 81(9): 2035–2046.
DOI:10.1175/1520-0477(2000)081 |
|
曾昭昭, 王晓峰, 任亮. 2017. 基于GWR模型的陕西秦巴山区TRMM降水数据降尺度研究[J]. 干旱区地理, 40(1): 26–36.
DOI:10.13826/j.cnki.cn65-1103/x.2017.01.004 |
|
杜灵通, 田庆久, 黄彦, 等. 2012. 基于TRMM数据的山东省干旱监测及其可靠性检验[J]. 农业工程学报, 28(2): 121–126.
DOI:10.3969/j.issn.1002-6819.2012.02.022 |
|
黄浠, 王中根, 桑燕芳, 等. 2016. 雅鲁藏布江流域不同源降水数据质量对比研究[J]. 地理科学进展, 35(3): 339–348.
DOI:10.18306/dlkxjz.2016.03.008 |
|
计晓龙, 吴昊旻, 黄安宁, 等. 2017. 青藏高原夏季降水日变化特征分析[J]. 高原气象, 36(5): 1188–1200.
DOI:10.7522/j.issn.1000-0534.2016.00119 |
|
江善虎, 任立良, 雍斌, 等. 2014. TRMM卫星降水数据在洣水流域径流模拟中的应用[J]. 水科学进展, 25(5): 641–649.
DOI:10.14042/j.cnki.32.1309.2014.05.006 |
|
江志红, 黄群, 李庆祥. 2008. 近50年中国降水序列均一性检验与订正研究[J]. 气候与环境研究, 13(1): 67–74.
|
|
李蒙, 秦天玲, 刘少华, 等. 2017. 怒江上游TRMM 3B42V7降水产品资料时空验证及降水特征分析[J]. 高原气象, 36(4): 950–959.
DOI:10.7522/j.issn.1000-0534.2016.00071 |
|
廖荣伟, 张冬斌, 沈艳. 2015. 6种卫星降水产品在中国区域的精度特征评估[J]. 气象, 41(8): 970–979.
DOI:10.13826/j.cnki.cn65-1103/x.2017.01.004 |
|
林厚博, 游庆龙, 焦洋, 等. 2016. 青藏高原及附近水汽输送对其夏季降水影响的分析[J]. 高原气象, 35(2): 309–317.
DOI:10.7522/j.issn.1000-0534.2014.00146 |
|
刘建军, 陈葆德. 2017. 基于CloudSat卫星资料的青藏高原云系发生频率及其结构[J]. 高原气象, 36(3): 632–642.
DOI:10.7522/j.issn.1000-0534.2017.00028 |
|
刘天仇. 1999. 雅鲁藏布江水文特征[J]. 地理学报, 54(S1): 157–164.
|
|
吕洋, 杨胜天, 蔡明勇, 等. 2013. TRMM卫星降水数据在雅鲁藏布江流域的适用性分析[J]. 自然资源学报, 28(8): 1414–1425.
|
|
齐文文, 张百平, 庞宇, 等. 2013. 基于TRMM数据的青藏高原降水的空间和季节分布特征[J]. 地理科学, 33(8): 999–1005.
DOI:10.13249/j.cnki.sgs.2013.08.017 |
|
孙乐强, 郝振纯, 王加虎, 等. 2014. TMPA卫星降水数据的评估与校正[J]. 水利学报, 45(10): 1135–1146.
DOI:10.13243/j.cnki.slxb.2014.10.001 |
|
唐国强, 万玮, 曾子悦, 等. 2015. 全球降水测量(GPM)计划及其最新进展综述[J]. 遥感技术与应用, 30(4): 607–615.
DOI:10.11873/j.issn.1004-0323.2015.4.0607 |
|
谢欣汝, 游庆龙, 保云涛, 等. 2018. 基于多源数据的青藏高原夏季降水与水汽输送的联系[J]. 高原气象, 37(1): 78–92.
DOI:10.7522/j.issn.1000-0534.2017.00030 |
|
许时光, 牛铮, 沈艳, 等. 2014. CMORPH卫星降水数据在中国区域的误差特征研究[J]. 遥感技术与应用, 29(2): 189–194.
DOI:10.11873/j.issn.1004-0323.2014.2.0189 |
|
许时光, 牛铮, 沈艳, 等. 2015. CMORPH对青藏高原地区夏季降水的模拟精度研究与修正[J]. 遥感信息, 30(1): 71–76.
DOI:10.3969/j.issn.1000-3177.2015.01.012 |
|
杨志刚, 卓玛, 路红亚, 等. 2014. 1961-2010年西藏雅鲁藏布江流域降水量变化特征及其对径流的影响分析[J]. 冰川冻土, 36(1): 166–172.
DOI:10.7522/j.issn.1000-0240.2014.0021 |
|
张立生, 孙建华, 赵思雄, 等. 2007. 长江中游暖切变型暴雨的分析研究[J]. 气候与环境研究, 12(2): 165–180.
DOI:10.3969/j.issn.1006-9585.2007.02.006 |
|
张蒙, 黄安宁, 计晓龙, 等. 2016. 卫星反演降水资料在青藏高原地区的适用性分析[J]. 高原气象, 35(1): 34–42.
DOI:10.7522/j.issn.1000-0534.2014,00152 |
2. Beijing Key Laboratory of Urban Hydrological Cycle and Sponge City Technology, Beijing 100875, China
 2019, Vol. 38
2019, Vol. 38
