2. 内蒙古自治区镫口扬水灌区管理局, 内蒙古 巴彦淖尔 014030
降水是水文循环重要的组成部分, 降水的变化对地球系统的水循环、能量循环、生态环境以及人类活动都有重要影响对地球气候系统有重要的反馈作用(宇如聪等, 2014)。由于云层的温度、气流分布等状况的差异, 降水具有不同的相态, 在中国降水的主要相态包括雨、雪、雨夹雪、冰粒、冰雹、冻雨等。降水相态一直是困扰着预报技术人员的一个难题, 相态的不同直接影响着预报的准确性, 即使很少的降水因相态的误报或漏报也会给人们的生活带来很大的影响(漆梁波等, 2012; Bocchieri et al, 2009; 胡爱军等, 2010)。在寒旱区草原流域降水的形态直接关系到降水的直接利用率, 如果降水以雪的形态产生, 在地表的累积不仅增加了地表反射率, 改变了地表的能量过程, 而且延迟了产汇流时间, 改变水循环过程。若以雨的形态产生会直接被土壤吸收或产生地表径流(Martyn et al, 2006; Czys et al, 1996)。降雪量的多少关系着寒旱区草原来年的牧草返青, 对草原春季旱情的防御有重要意义, 当然降雪也会产生雪灾, 对农牧业产生不可挽回的经济损失。所以对降雪的识别、预报有着十分重要的现实意义(席小康等, 2016; 董振华等, 2016)。
近年来国内外学者对降水相态识别的研究主要以气象学研究为主, 研究者是以大气层的温度、厚度为准的垂直廓线, 对降水的相态进行识别判断(漆梁波等, 2012; 刘少华等, 2018)。温度的改变会直接影响到降水的相态, 极小的温度变化都可能使降水的相态发生改变, 如漆梁波等(2012)对中国东部地区冬季降水相态研究中指出, 通过温度平均廓线, 可较好地区分出雨和雪。隋玉秀等(2015)在对大连地区冬季降水相态的预报方法研究中发现, 从各个距地面等间隔气层的平均气温对相态的识别情况来看, 距地面220~60 hPa的高度层最为重要, 是影响降水相态变化的关键层。降水相态的相态转换存在一个温度的临界值, 在该值附近些微的变化就可能引起相态的转变。张俊兰等(2017)在对新疆出现的一次大范围雨转雪天气和强降雪过程进行天气诊断, 分析降水相态变化过程时发现, 中低层温度是预报降雪相态转换的关键气象因子, T500 < -25 ℃和T700 < -12 ℃是雨夹雪转雪的临界温度, T850 < -2 ℃和T925 < 2 ℃时雨转雨夹雪, T850 < -4.5 ℃(T*表示距地面*米高空气温)用来判别雨夹雪转雪。由于气象资料的稀缺性, 目前关于雨雪的转换过程一般使用天气动力学的方法, 降水相态的识别多集中于统计学上的方法, 包括单温度阈值法和双温度阈值法(胡顺起等, 2017; 张志杰等, 2017; Yang et al, 1997; Chen et al, 2007; 韩春坛等, 2010)。如刘少华等(2018)在怒江流域利用双温度阈值法进行了降雪的识别, 结果表明该方法可较好的估计怒江上游流域各气象站点降雪量。所研究的气象站点所估计降雪量与总降雪量相关性很高, 误差较小。张琳娜等(2013)在不同海拔与气流强弱条件下用单温度法对北京的降水相态进行了识别判断。单温度阈值法是寻求一个温度临界值, 当温度大于临界温度则视降水全部为降雨, 小于临界温度视降水全部为降雪, 忽略了各降水相态间存在着一个相互交织的缓冲温度区间。这种方法有一定的误差, 无论是降雨还是降雪的发生都不可能是在一个特定临界温度, 在外部环境的影响下降水的相态会有很大差异, 而不同地区临界温度也会有差异(韩春坛等, 2010), 所以单温度阈值法在实际运用中会产生较大的误差。双温度阈值法考虑了降水相态识别的缓冲温度区间, 提高了降雪识别的准确性, 较单温度阈值法精度高, 目前在多个地区得到了运用。后来研究者发现在双温度阈值法中加入指数方程进行概率模拟, 可提高该方法的精度(刘少华等, 2018)。
锡林河流域位于内蒙古自治区锡林郭勒草原, 是该地区最主要的地表径流, 属大陆性温带半干旱大陆性气候是典型的寒旱区草原, 降水稀少, 其中降雪量占全年降水量比重较大, 降雪的多少直接影响着未来研究区生态、农牧业等方面的发展, 但由于现今降雪观测技术的局限性, 降雪量数据的获取及降雪演变趋势的研究一直是困扰着研究者的一个难题。为此本文旨在寻求一种可准确获得降雪量的方法进而对区域降雪量的趋势变化进行分析研究, 以期为寒旱区草原流域降水相态的识别、预报以及地区生态保护、农牧业发展等方面的科学研究提供一定参考。
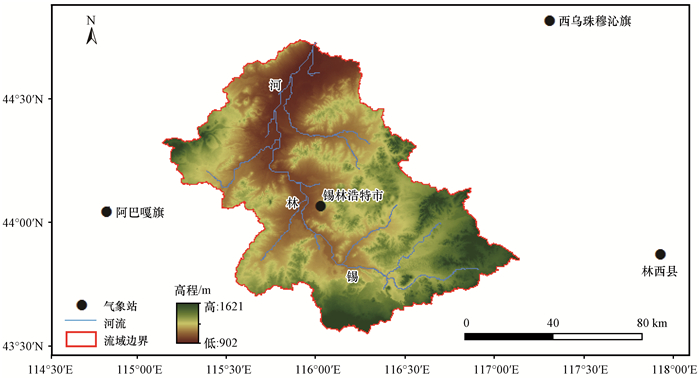
2 资料来源及方法介绍 2.1 数据资料在1979年之前的国家气象站所提供的降水资料标记了降水相态, 可利用1979年之前的日降水与日平均气温资料采用双温度阈值法对锡林河流域的降雪进行识别, 但由于研究区锡林河流域气象站点(图 1)较少气象资料稀缺, 单站的气象资料时间序列短数据量不足, 缺少代表性, 故本文选取锡林河流域内的气象站锡林浩特站及距离流域较近的阿巴嘎旗、林西县、西乌珠穆沁旗4个国家气象站的1969—2016年的气象资料, 利用1969—1979年降水与平均气温逐日资料确定温度阈值与指数方程, 取1979—2016年的逐日降水与气温数据对其降雪量进行估计。
|
图 1 锡林河流域站点分布 Fig. 1 The meteorological stations distribution of the Xilin River Basin |
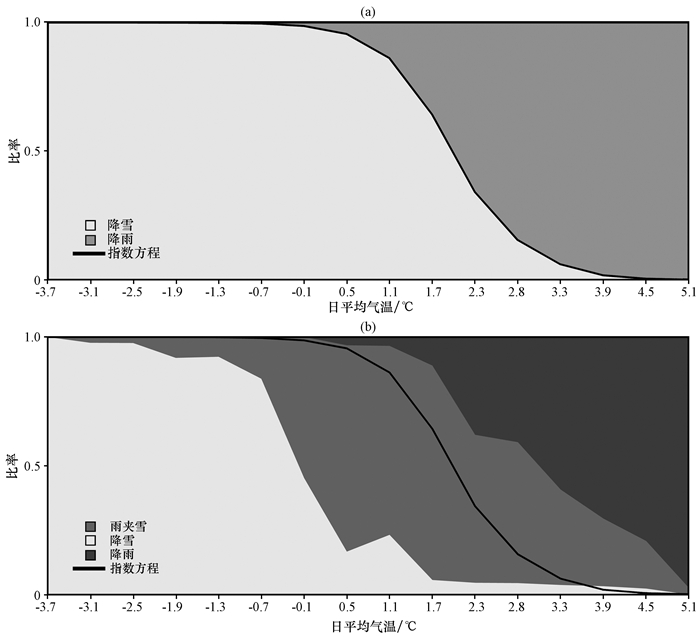
在研究区各个站点, 利用双温度阈值法, 对降雪量进行识别, 选取4个站点(图 1)1969—1979年降水与平均气温逐日资料, 从逐日降水相态与平均气温数据中找出降雪的温度两个阈值, 统计不同温度下降雪量占总降水量的比率, 绘制降雪比率与温度之间的关系[图 2(a)不包括雨夹雪的情况]。当日平均气温大于等于最大温度阈值时降水全部为降雨, 降雪比率为0, 小于等于最小温度阈值时降水全部为降雪, 降雪比率为1, 当日平均气温在临界温度之间是降雪比率服从S型指数函数(许美玲等, 2015; Liu et al, 2016; Ding et al, 2014)。利用甄选出的临界温度与指数方程, 结合各年的降水与平均气温数据对降雪进行识别并估计出降雪量。指数方程具体如下:
|
图 2 研究区降水相态与平均气温的关系 Fig. 2 Relationship between precipitation phases and average temperature in the study area |
| ${P_s} = \frac{1}{{1 + \exp (a + bT)}}\,\,\,\, , $ | (1) |
式中: Ps为降雪比例; T为日平均温度; a、b为方程经验参数, 由研究区域气温与降雪比例通过最小二乘法估算得到(本文估算得a=-4.11, b=2.07)。
对雨夹雪中降雪比例的估计需假设在相同温度下雨夹雪可分为降雪与降雨, 其降雪比例也满足上述指数方程。以此为根据统计不同温度下降雪量, 降雨量和雨夹雪占该温度降水总量的比例。绘制平均温度与降水各相态比例的关系图[图 2(b)]。将研究区各气象站点的雨夹雪中的估计所得的降雪量与真实观测降雪量相加得到总降雪量, 并以此为据对指数方程识别的降雪量进行验证(Liu et al, 2016)。
2.2.2 Mann-Kendall突变检验将识别的各个站点1979—2016年每年的逐日降雪量累积相加得到各年年降雪量, 采用Mann-Kendall检验法对1969—2016年的年降雪量进行突变检验, 找到降雪量突变时间点, 将流域各站点的共同突变时间点确定为典型突变点。计算公如下:
对于一个含有n个样本时间序列X, 首先构造一秩序列:
| ${S_k} = \sum\limits_{i = 1}^k {{r_i}}, \;\;\;(k = 2, 3, \cdots, n)$ | (2) |
| ${r_i} = \left\{ {\begin{array}{*{20}{l}} { + 1}&{{\rm{ if}}\;{x_j} > {x_i}}\\ 0&{{\rm{ if}}\;{x_j} \le {x_i}} \end{array}, \;\;\;\;(j = 1, 2, \cdots, i)} \right.$ | (3) |
式中:秩序列Sk表示第i时刻大于第j时刻数值的累积个数。假设时间序列相互独立, 定义统计量:
| $U{F_k} = \frac{{\left[ {{S_k} - E\left({{S_k}} \right)} \right]}}{{\sqrt {{\mathop{\rm Var}\nolimits} \left({{d_k}} \right)} }}, \;\;\;(k = 1, 2, \cdots, n)$ | (4) |
式中: UF1=0, E(Sk)和Var(dk)是Sk的均值和方差, 当产生的随机序列近似服从正太分布时, E(Sk)、Var(dk)计算公式如下:
| ${E\left({{S_k}} \right) = k(k - 1)/4, }$ | (5) |
| ${{\mathop{\rm Var}\nolimits} \left({{d_k}} \right) = k(k - 1)(2k + 5)/72, }$ | (6) |
按照时间序列X逆序X′={Xn, Xn-1, …X1}, 重复上述过程, 得到UFk, 计算UBk, 使得UBk=-UFk。
分别绘制UFk、UBk曲线图, 若UFk或UBk的值大于0, 则表明序列呈上升趋势, 反之, 序列呈下降趋势。当它们超过临界线时, 表明上升或下降趋势显著, 此时, 超出的范围定义为出现突变的时间区域。若它们在置信区间内相交, 则该点被定义为时间序列的突变点(Dai et al, 2008; 金成浩等, 2013)。
2.2.3 气候变化对降雪量变化的贡献分析在全球气候变化的背景下, 近年来极端天气、气候事件的发生频率和发展强度都在急剧增加(黄小燕等, 2015), 降雪作为降水的特殊形式, 在气候变化的影响下变化格外活跃。为直观反映气候变化对降雪量的影响, 取流域中心最具代表性的锡林浩特站为例, 选取降水与温度两个气象要素进行情景模式的设立, 研究降水与温度改变对降雪量变化的贡献, 根据Mann-Kendall检验出的降雪量突变点, 在突变点之后设置气候变化情景模式, 人为模拟造成气象因子的变化, 所以将研究序列1969—2016年划分为气候变化前与气候变化后两个阶段。锡林河流域冬季降雪期为10月至次年4月, 以气候变化前多年降雪期的各月平均降雪量作为基准值(S0), 以气候变化后降雪期各月平均降雪量作为气候变化后降雪量(Sa)。根据锡林河流域1996年以后气温与降水量都呈上升趋势的已有研究成果(冯新灵等, 2009; 宋小园等, 2016), 设立温度与降水变化情景下模拟方案, 量化反映二者变化对降雪量变化的贡献。
气温变化模拟方案:用无趋势逐日平均气温系列对降雪量进行识别估计, 首先计算气候变化后各年平均气温的增长速率, 然后将其每年逐日平均气温减去该年平均气温增量, 获得相应时间序列的去趋势化逐日气温系列。根据去趋势化逐日平均气温与对应的降水量, 再利用双温度法与指数方程对气候变化后降雪期的降雪进行识别, 并估计其逐日降雪量, 得到降雪期气温变化下的各月平均降雪量(ST)。
降水变化模拟方案:通过图 2可知, 降雪比例随温度变化而变化, 温度不变降雪比例不变, 即特定温度下降雪率(降雪量/降水量)是一定的。所以降水变化方案是将气候变化后降雪期各月平均降雪率乘以气候变化前降雪期各月平均降水量, 进而得到降水变化下的降雪期各月平均降雪(SP)(刘少华等, 2018)。
根据温度与降水的变化模拟方案下所得到的降雪量, 分别计算气温变化、降水变化和二者共同变化影响对降雪量改变的贡献率CT、CP和CT&P。计算公式如下:
| ${{C_T} = \frac{{{S_a} - {S_T}}}{{{S_0}}}, }$ | (7) |
| ${{C_p} = \frac{{{S_a} - {S_P}}}{{{S_0}}}, }$ | (8) |
| ${{C_{{\rm{T\& P}}}} = \frac{{{S_T} + {S_P} - {S_0} - {S_a}}}{{{S_0}}}, }$ | (9) |
以上所计算的贡献率其理论取值范围为[-1, +∞), 负值表示该要素的增加/升高对降雪量的增加具有负贡献, 一般情况下三个贡献率之和不为1。
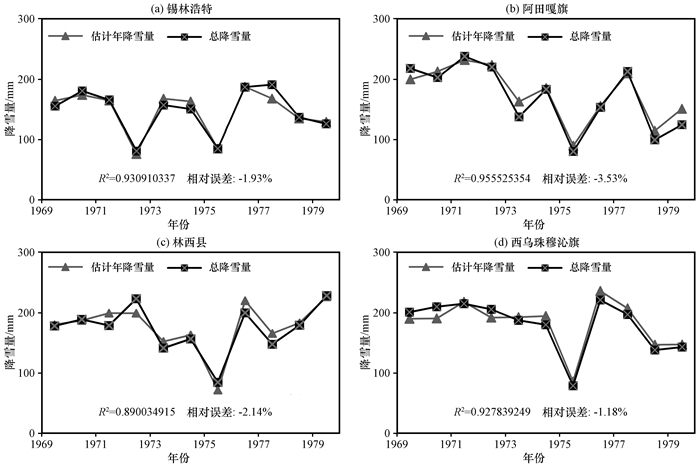
3 结果与分析 3.1 降雪识别与验证利用研究区4个国家气象站1969—1979年的气温与降水及其相态数据, 统计得出气温与降雪比例的关系, 确定出了临界温度, 分别是-3.7 ℃和5.1 ℃。在临界温度区间内(-3.7~5.1 ℃), 拟合得到指数方程。根据临界温度与指数方程对研究区内4个站点1969—1979年的降雪进行识别, 得到1969—1979年的估计降雪量, 将估计降雪量与总降雪量(识别雨夹雪中降雪量和真实降雪量相加所得)进行比较, 以验证降雪识别方法的可靠性。如图 3所示, 研究区各站点1969—1979年年估计降雪量与总降雪量都具有较好的相关性, 除林西站其他3个站点的相关系数都达到了0.9以上, 变化趋势表现出较高的一致性, 其中阿巴嘎旗站的相关系数最高, 超过了0.95。从图 3中还可以看出, 在1974—1976年各站点的估计降雪量与总降雪量几乎一致偏差很小, 从识别降雪的方法考虑, 这可能是由于此阶段研究区降水相态中雨夹雪出现的次数较少, 所以模拟结果优于其他年份。各站点相对误差都表现为负值, 均低估了实际降雪量, 但误差都在4%以内, 偏差量值较小, 对整体趋势变化影响不大, 在允许误差范围内。
|
图 3 1969—1979年研究区各站点估计年降雪量与总降雪量 Fig. 3 Estimated annual snowfall and total snowfall at each site in the study area from 1969 to 1979 |
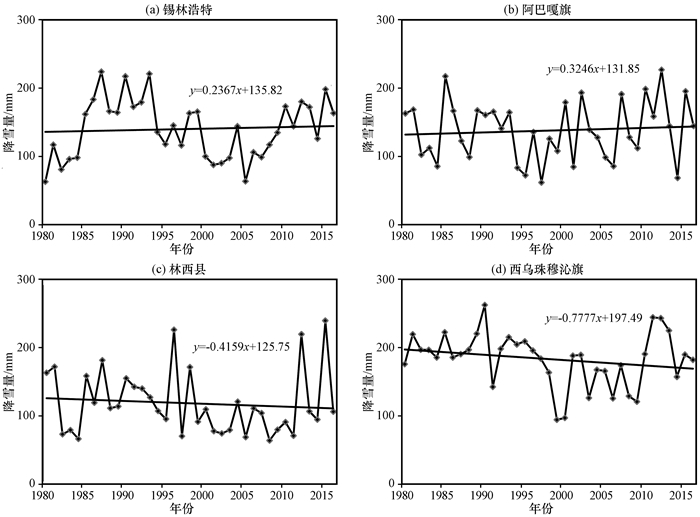
根据临界温度与指数方程识别降雪, 得到1980—2016年锡林河流域各站点的估计降雪量。作研究区各站点估计年降雪量线性变化趋势(图 4)可知, 锡林浩特与阿巴嘎旗两个站点降雪量呈增加趋势, 而林西县站与西乌珠穆沁旗站降雪量则呈下降趋势, 也可从图 4中看出西乌珠穆沁旗站降雪量明显大于其他站点。
|
图 4 1980—2016年研究区各站点估计降雪量 Fig. 4 Estimated snowfall at each site in the study area from 1980 to 2016 |
为更加直观反应研究区各站点降雪量的变化趋势, 寻找流域的突变典型突变点, 利用Mann-Kendall突变检验法检验各站点1969—2016年期间的突变情况如图 5所示, 根据Mann-Kendall突变检验结果可知锡林浩特站正序列曲线UF与反序列曲线UB有1980, 1985, 1995, 2011和2014年5个有效的交点, 故得出锡林浩特站降雪量可能在这5年发生突变。林西县Mann-Kendall突变检验的正序列曲线UF与反序列曲线UB有2个有效交点, 分别是1976年与1981年, 因此突变点应为1976年和1981年, 西乌珠穆沁旗有2个突变点分别为1980年和1995年, 阿巴嘎旗只存在1972年1个突变点。观察所研究的4个站点的突变情况, 不难看出锡林河流域降雪量除阿巴嘎旗其余3个站点均在1980年左右产生突变, 结合目前普遍认可的1980年作为研究区降水突变点的研究成果(冯新灵等, 2009; 尹云鹤等, 2009; 李喜仓等, 2013; 宋小园等2016), 将1980年视为流域的典型突变点。
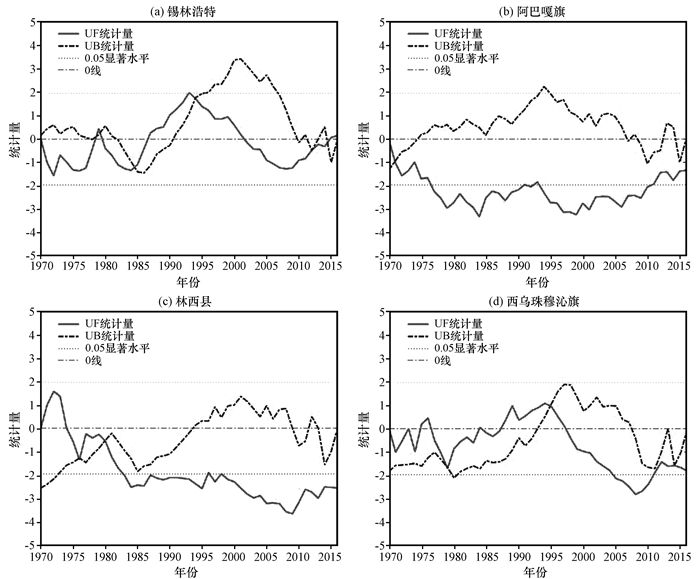
|
图 5 1969—2016年研究区各站点估计降雪量的Mann-Kendall突变检验 Fig. 5 Mann-Kendall mutation test for estimated snowfall at each site in the study area from 1969 to 2016 |
根据Mann-Kendall突变检验结果, 选取锡林浩特站以典型突变点1980年为界, 将1969—2016年划分为气候变化前(1969—1979年)与气候变化后(1980—2016年)两个阶段。对比气候变化前后各月平均降雪量S0、Sa可发现(图 6), 除10月外, 其他几个月气候变化前的降雪量都小于气候变化后的降雪量, 降雪量有增长趋势。通过计算气候变化前降雪期(10月至次年4月)各月降雪量为基准值(S0)、气候变化后降雪量(Sa)、模拟气温变化下的降雪期各月平均降雪量(ST)和模拟降水变化下的降雪期各月平均降雪量(SP), 可得到气温变化、降水变化和二者共同变化影响对降雪量改变的贡献率CT、CP、CT&P(图 7)。从图 7降雪率曲线可知, 锡林浩特站的降雪率曲线呈凹字形, 在1月和12月降雪率为100%降水全部为降雪, 2月的降水中有94.87%是降雪, 3月与11月降雪率也超过了50%。相对于其他月份4月与10月降雪率较小, 分别为27.54%和29.59%。在改变气温条件下, 气温的上升在1月与12月对降雪量没有影响, 这可能是因为其基础温度很低, 温度的增加不足以使气温变化到临界温度, 不会对降水的相态及降雪量产生影响。其他月份气温变化对降雪量的增加均表现出负贡献, 对降雪量有减少的作用, 且在10月份贡献率最大为-29.13%, 减少作用最突出。降水改变条件下, 降水的增加在降雪期各月对降雪量的增加都呈现出正贡献, 对降雪量有明显增加作用, 且在4月贡献率为49.99%, 作用最为明显。气温、降水共同作用影响下, 两者的改变对降雪量的增加都表现为正贡献, 对降雪量呈现增加作用, 其中除4月和10月外在各月贡献率高于降水改变条件下的贡献率。从识别降雪的方法考虑, 其原因可能是1, 2, 3, 11和12月基础气温较低, 温度升高值不足以达到降雪与降水分界阈值, 所以气候变化条件下温度仍处在降雪温度临界值之内, 在低温作用下降水概率的增加对于降雪量增加具有显著促进作用(刘少华等, 2018)。
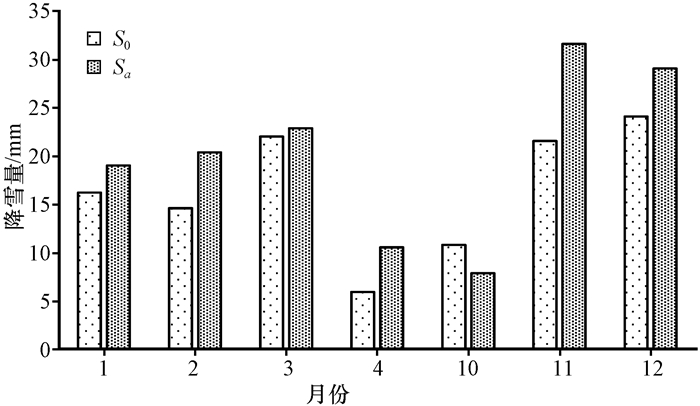
|
图 6 锡林浩特站气候变化前(1969—1979年)和气候变化后(1980—2016年)降雪期各月平均降雪量 Fig. 6 Average snowfall per month before (from 1969 to 1979) and after (from 1980 to 2016) the climate change in Xilinhot Station |
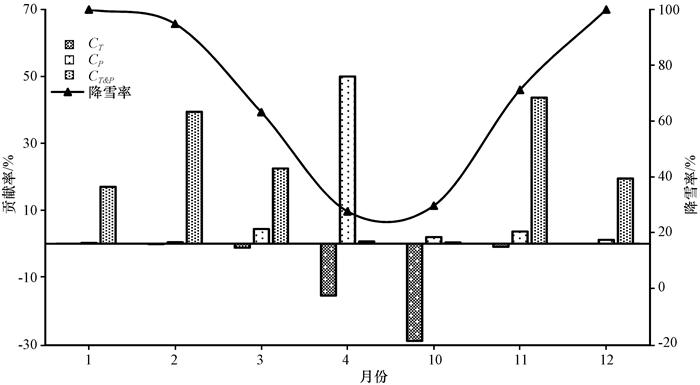
|
图 7 锡林浩特站气候变化后(1980—2016年)降雪期各月的降雪率及各因素对降雪量变化的贡献率 Fig. 7 After the climate change in Xilinhot Station (from 1980 to 2016), the snowfall rate during the snow period and the contribution rate of various factors to the change of snowfall |
(1) 经统计研究区各站点的气温与降水及其相态数据, 得出气温与降雪比例的关系, 确定出了降雪临界温度为-3.7 ℃与5.1 ℃, 拟合得到降雪识别方程。利用双温度法与识别方程识别降雪, 所得的1969—1979年估计降雪量与总降雪量具有很好相关性, 在研究区各站点的误差均在4%以内, 能够较为准确的估计年降雪量。
(2) 1980—2016年锡林河流域各站点的估计降雪量的变化趋势并不一致, 锡林浩特与阿巴嘎旗两个站点降雪量呈增加趋势, 而林西县站与西乌珠穆沁旗站降雪量则呈下降趋势, 从站点分布空间来看, 锡林浩特与阿巴嘎旗站分布于流域西侧, 林西县与西乌珠穆沁旗站分布于东侧, 整个流域降雪量呈现出东增西减的趋势。
(3) 经过Mann-Kendall突变检验, 发现在1980年左右除阿巴嘎旗外流域内各站点降雪量均产生突变, 故确定1980年为流域的典型突变点。
(4) 取锡林浩特站设立气温与降水变化情景下模拟方案, 发现气温的上升对除1月与12月外的降雪期各月的降雪量变化是负贡献, 对降雪量有减少的作用, 降水增加则对降雪期各月的降雪有增加作用, 气温与降水共同作用对降雪量的增加呈现正贡献, 会促进降雪量的增加。
在锡林河流域降雪量可用双温度法与识别方程估计得到, 准确性较好, 所以该方法也可用于同类型流域识别降雪。锡林河流域冬季寒冷气温较低, 在降雪期的12月和1月气温的小幅度变化不会影响降雪量, 若进行大胆推测, 在全球变暖的气象环境下, 在降雪期各月如遇较低的气温与降水同时出现, 降雪发生的概率和降雪量都会增加。本研究仅限于利用温度对降雪识别, 而降雪的形成过程极其复杂, 所以单一的根据气温识别降雪有一定局限性, 后续研究可综合考虑气温、降水、大气压强等因素对降雪进行识别。另外由于研究区国家气象站点较少, 站点分布又较为分散, 导致站点数据代表性有限, 所以若需精准流域的降雪量数据需加密站点作深入研究。
Bocchieri J R. 2009. The objective use of upper air soundings to specify precipitation type[J]. Monthly Weather Review, 108(5): 596–603.
|
|
Chen R, Lu S, Kang E, et al. 2007. A distributed water-heat coupled model for mountainous watershed of an inland river basin of Northwest China (Ⅰ) model structure and equations[J]. Environmental Geology, 53(6): 1299–1309.
|
|
Czys R R, Scott R W, Tang K C, et al. 1996. A physically based, nondimensional parameter for discriminating between locations of freezing rain and ice pellets[J]. Weather & Forecasting, 11(4): 591–598.
|
|
Dai A. 2008. Temperature and pressure dependence of the rain-snow phase transition over land and ocean[J]. Geophysical Research Letters, 35(12): 62–77.
|
|
Ding B, Yang K, Qin J, et al. 2014. The dependence of precipitation types on surface elevation and meteorological conditions and its parameterization[J]. Journal of Hydrology, 513(11): 154–163.
|
|
Liu S, Yan D, Qin T, et al. 2016. Precipitation phase separation schemes in the Naqu River basin, eastern Tibetan plateau[J]. Theoretical & Applied Climatology, 131(1/2): 1–13.
|
|
Martyn P C, Andrew G S, Andrew P B, et al. 2006. Assimilation of snow covered area information into hydrologic and land-surface models[J]. Advances in Water Resources, 29(8): 1209–1221.
DOI:10.1016/j.advwatres.2005.10.001 |
|
Yang Z L, Dickinson R E, Robock A, et al. 1997. Validation of the snow submodel of the biosphere-atmosphere transfer scheme with Russian snow cover and meteorological observational data[J]. Journal of Climate, 10(2): 353–373.
DOI:10.1175/1520-0442(1997)010<0353:VOTSSO>2.0.CO;2 |
|
宇如聪, 李建, 陈昊明, 等. 2014. 中国大陆降水日变化研究进展[J]. 气象学报, 72(5): 948–968.
|
|
董振华, 张继权, 佟志军, 等. 2016. 锡林郭勒盟草原雪灾社会影响评价[J]. 自然灾害学报, 25(2): 59–68.
|
|
冯新灵, 罗隆诚, 冯自立. 2009. 中国近50年降水变化趋势及突变的Hurst指数试验[J]. 干旱区地理, 32(6): 859–866.
|
|
韩春坛, 陈仁升, 刘俊峰, 等. 2010. 固液态降水分离方法探讨[J]. 冰川冻土, 32(2): 249–256.
|
|
胡爱军, 李宁, 祝燕德, 等. 2010. 论气象灾害综合风险防范模式——2008年中国南方低温雨雪冰冻灾害的反思[J]. 地理科学进展, 29(2): 159–165.
|
|
胡顺起, 曹张驰, 陈滔. 2017. 山东省南部一次极端特大暴雪过程诊断分析[J]. 高原气象, 36(4): 984–992.
DOI:10.7522/j.issn.1000-0534.2016.00134 |
|
黄小燕, 李耀辉, 冯建英, 等. 2015. 中国西北地区降水量及极端干旱气候变化特征[J]. 生态学报, 35(5): 1359–1370.
|
|
金成浩, 韩京龙. 2013. 基于Mann-Kendall检验的嘎呀河流域降水变化趋势及突变分析[J]. 吉林水利(12): 62–66.
|
|
刘少华, 严登华, 王浩, 等. 2018. 怒江上游流域降雪识别及其演变趋势和原因分析[J]. 水利学报, 49(2): 254–262.
|
|
李喜仓, 王冀, 杨晶. 2013. 内蒙古东部牧区极端降雪变化特征及其成因[J]. 地理科学, 33(7): 884–889.
|
|
漆梁波, 张瑛. 2012. 中国东部地区冬季降水相态的识别判据研究[J]. 气象, 38(1): 96–102.
|
|
宋小园, 朱仲元, 张圣微, 等. 2016. 锡林河流域气候变化特征诊断分析[J]. 干旱区资源与环境, 30(4): 151–158.
|
|
隋玉秀, 杨景泰, 王健, 等. 2015. 大连地区冬季降水相态的预报方法初探[J]. 气象, 41(4): 464–473.
|
|
许美玲, 梁红丽, 金少华, 等. 2015. 昆明冬季降水相态识别判据研究[J]. 气象, 41(4): 474–479.
|
|
席小康, 朱仲元, 宋小园, 等. 2016. 锡林河流域融雪径流时间变化特征与成因分析[J]. 水土保持研究, 23(6): 150–153.
|
|
尹云鹤, 吴绍洪, 陈刚. 2009. 1961-2006年我国气候变化趋势与突变的区域差异[J]. 自然资源学报, 24(12): 2147–2157.
|
|
张俊兰, 彭军. 2017. 北疆春季降水相态转换判识和成因分析[J]. 高原气象, 36(4): 939–949.
DOI:10.7522/j.issn.1000-0534.2016.00094 |
|
张琳娜, 郭锐, 曾剑, 等. 2013. 北京地区冬季降水相态的识别判据研究[J]. 高原气象, 32(6).
DOI:10.7522/j.issn.1000-0534.2012.00147 |
|
张志杰, 王志楠. 2017. 呼和浩特市降水相态识别判据研究[J]. 内蒙古林业科技, 43(1): 42–47.
DOI:10.3969/j.issn.1007-4066.2017.01.012 |
2. Dengkou Water Pumping Irrigation District Administration of Inner Mongolia, Bayannur 014030, Inner Mongolia, China
 2019, Vol. 38
2019, Vol. 38
