20世纪以来, 随着全球变暖趋势的进一步加剧(张莉等, 2013), 极端天气和气候事件频出, 而极端气候事件尤其是极端降水事件对气候变暖的响应尤为敏感(You et al, 2011; 胡芩等, 2015; 高涛等, 2014; 高歌等, 2008; 周莉等, 2019; 黄安宁等, 2004; 刘维成等, 2017)。因此, 极端降水事件的变化得到了广泛而持续的关注(黄安宁等, 2004; 翟盘茂等, 2007; Zhou et al, 2006; 王小玲等, 2008; 周莉等, 2018; Jiang et al, 2012)。湖南降水充沛, 洪涝灾害频繁, 全年大部分降水量集中在雨季, 极端降水事件的区域性特征显著(周莉等, 2019; 李博等, 2010; 熊伟等, 2006; 李红梅等, 2008; 曾小凡等, 2009; 苏布达等, 2006; 廖玉芳等, 2012; 陆魁东等, 2007; 王爱珍等, 2008; 张瑞等, 2011; 张剑明等, 2008; 桓玉等, 2018)。因此湖南地区极端降水事件对气候变化的响应相较于其他地区敏感度更强, 对湖南极端降水进行精细化预估尤为重要。

以上研究利用大气环流模式(GCM)模拟未来气候变化特征, 该模拟方法已被证实是研究未来气候变化较为有效的手段之一, 但预估结果往往并不一致(曾小凡等, 2011; 周秀华等, 2014; 赵天保等, 2014; 张武龙等, 2015; 张增信等, 2007; 张蓓等, 2017; 伍清等, 2017), 因此对当前气候的模拟能力进行多方位评估是十分重要的。初祁等(2015)评估了CMIP5模式对长江中下游流域降水的模拟能力, 发现在空间尺度上模式集合的空间分布趋势与观测值大致相同, 但对其空间分布特征的模拟尚不可达到精准。

降尺度技术可将大尺度气候信息转化为区域尺度的气候信息, 从而减小区域降水的模拟误差, 提高模式模拟能力(赵芳芳等, 2007; 刘向培等, 2012; 崔妍等, 2010; 刘吉峰等, 2008)。本文采用CDF-t统计降尺度方法, 最早是由Michelangeli et al(2009)提出来的, 发现该方法对风速的模拟较为准确。周莉等(2017)使用CDF-t统计降尺度方法对湖南日降水量进行模拟, 发现基于CDF-t的统计降尺度方法的CMIP5模式模拟湖南降水的时空分布与实况更为接近。极端降水的模拟对提高应对气候变化的决策服务质量有着更为重要的现实意义, 湖南地区由于复杂的地形和气候条件, 极端降水的模拟一直是一个难题。因此, 利用CDF-t降尺度方法和实况资料对CMIP5提供的24个气候模式输出的历史逐日降水数据进行降尺度处理, 评估该降尺度方法对湖南极端降水时空分布的模拟能力。

所用实况资料为1961—2005年湖南省内国家基准气象站的逐日降水量数据(由湖南省气象信息中心提供)。模式资料为CMIP5提供的24个海气耦合模式(表 1)同时段的历史逐日降水数据。由于模式与实况, 以及各模式之间的分辨率并不一致, 因此利用双线性方法将实况数据和模式数据统一进行插值处理到相同格点上, 分辨率为0.5°×0.5°。本文将1961—2005年分为两段:建模时段(1961—1980年)和验证时段(1981—2005年), 前者用于将观测和模式数据建立降尺度模型, 后者用于检验评估。

表 1(Table 1)

表 1 24个CMIP5全球模式的基本信息 Table 1 Basic information on the 24 climate models of CMIP5 模式名称 分辨率 ACCESS1-0 192×145 ACCESS1-3 192×145 BCC-CMS1-1 128×64 BCC-CSM1-1m 320×160 BNU-ESM 128×64 CanCM4 128×64 CanESM2 128×64 CCSM4 288×192 CMCC-CM 480×240 CMCC-CMS 192×96 CNRM-CM5 256×128 FGOALS-s2 128×108 GFDL-ESM2G 144×90 GFDL-ESM2M 144×90 HadGEM2-CC 192×145 HadGEM2-ES 192×145 IPSL-CM5A-LR 96×96 IPSL-CM5A-MR 144×143 MIROC5 256×128 MIROC-ESM 128×64 MIROC-ESM-CHEM 128×64 MPI-EMS-LR 192×96 MPI-EMS-MR 192×96 MRI-CGCM3 320×160 NorESM1-ME 144×96

表 1 24个CMIP5全球模式的基本信息 Table 1 Basic information on the 24 climate models of CMIP5

引入3个极端降水指数(Frich et al, 2002; 周莉等, 2018)来考核原模式和CDF-t降尺度方法对极端降水的模拟能力(表 2)。对CMIP5和观测格点分别计算1961—2005年每年的极端降水指数。

表 2(Table 2)

表 2 极端指数基本信息 Table 2 Basic information of indices 序号 指数名称 缩写 定义 1 大雨日数/d R10 日降水量大于10 mm的天数 2 极端降水阈值/mm R90P 位于90%分位数的降水量 3 连续5天最大降水量/mm R5d 最大的连续5日总降水量

表 2 极端指数基本信息 Table 2 Basic information of indices

CDF-t降尺度方法是将两个变量累计概率分布函数建立联系, 即较大尺度的原变量和较小尺度也是目标尺度的观测变量(穆振侠等, 2015; 刘绿柳等, 2012; Piani et al, 2010; 周莉等, 2017), 通过转移函数T使得原变量和观测变量的CDF接近。图 1为CDF-t统计降尺度方法核心示意图[该图基于湖南省标准地图服务网站下载的审图号为GS(2016)1605的标准地图制作, 底图无修改], 此转移函数的意义其实就是对于某一个变量X, 建立历史时期观测(F₁)与模式(F₂)CDF的函数关系(箭头3)(周莉等, 2017)。此转移函数在验证时期保持不变(即箭头3平移至F₃), 通过验证时期模式CDF(F₃)后, 整个过程按照箭头顺序进行, 最终得到降尺度之后的CDF(实心圆点)。CDF-t统计降尺度通过建立大尺度变量的CDF与区域尺度相同变量的CDF之间的函数关系, 很大程度上节约了运算资源。

图 1(Fig. 1)

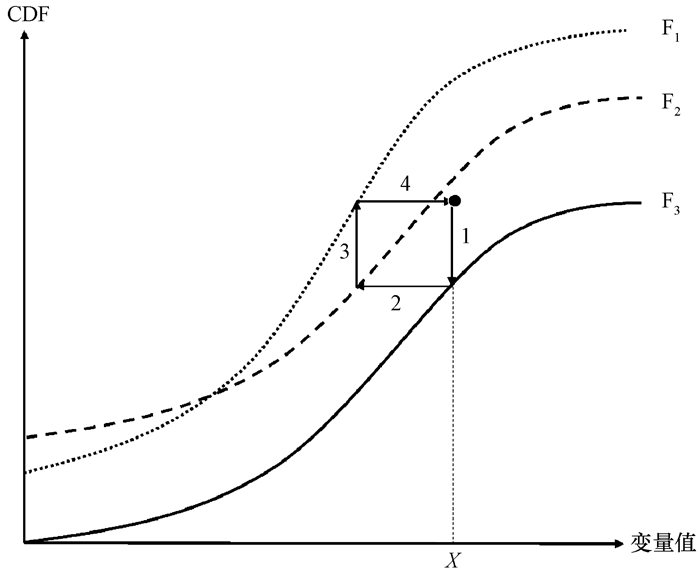
图 1 CDF-t统计降尺度的核心思想示意图 Fig. 1 Schematic diagram of core thought in the statistical downscaling method of transform cumulative distribution function

使用年际变率指标(IVS)来定量评估降尺度前后模式对某一变量年际变率的模拟能力, 即:

式中: STD_m为模式的标准差; STD_o为观测变量的标准差。当模式模拟IVS与观测变量IVS越接近, 模拟结果越准确(周莉等, 2018)。

图 2为CDF-t降尺度前后24个气候模式模拟湖南极端降水指数的泰勒图(Taylor, 2011)。从图 2中可以看出, 对于R10、R90P和R5d三个极端降水指数, 从相关系数、均方根误差和标准差三项指标来看, CMIP5气候模式不能准确的模拟出湖南极端降水的空间结构特征, 在降尺度前各模式在泰勒图上分布较为分散, 针对以上三项的各模式评估结果差异较大。降尺度后CMIP5气候模式对于湖南极端降水的空间结构特征的模拟能力有显著提高, 对于R10和R5d来说, 降尺度改进效果是非常显著的, 经过降尺度处理之后, 各模式在泰勒图上分布较为集中, 除个别模式以外, 大部分模式在降尺度之后都能够模拟出R10和R5d实况的空间分布特征(相关系数> 0.5)。此外, 70%模式模拟的空间分布接近观测结果(两者标准差比约等于1), 尤其是R10, 几乎所有模式都在代表“1”的曲线附近分布, 表明能够很好地模拟出R10和R5d的空间差异。除了个别模式对于R5d的模拟与观测的均方根误差大于1.0以外, 所有模式对于R10的模拟以及大部分模式对于R5d的模拟与观测的均方根误差均在1.0以内, 表明降尺度后R10和R5d在变化幅度上与观测非常接近。但是对于R90P, CDF-t统计降尺度方法对于其空间结构特征模拟的改进效果则不是特别理想。值得一提的是, 日本大气海洋研究所的模式MIROC5在降尺度处理之后能够表现出较好的模拟效果。

图 2(Fig. 2)

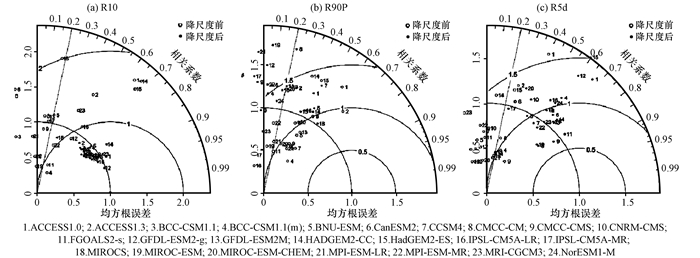
图 2 24个气候模式模拟湖南极端降水指数的泰勒图 Fig. 2 Taylor diagram of the extreme precipitation indices in Hunan for 24 climate models

图 3用盒须图展示24个气候模式模拟极端降水指数与观测的绝对误差, 进一步检验CDF-t对模式模式极端降水空间结构能力的改进效果。图 3中最上端的和最下端的短横线“-”表示极端降水指数与观测之间绝对误差序列95%和5%的分位数值, 长方框中的粗黑线(该线不一定位于长方框正中间)表示极端降水指数与观测之间绝对误差序列中位数值, 长方框上下边缘细黑线表示极端降水指数与观测之间绝对误差序列75%和25%的分位数值。

图 3(Fig. 3)

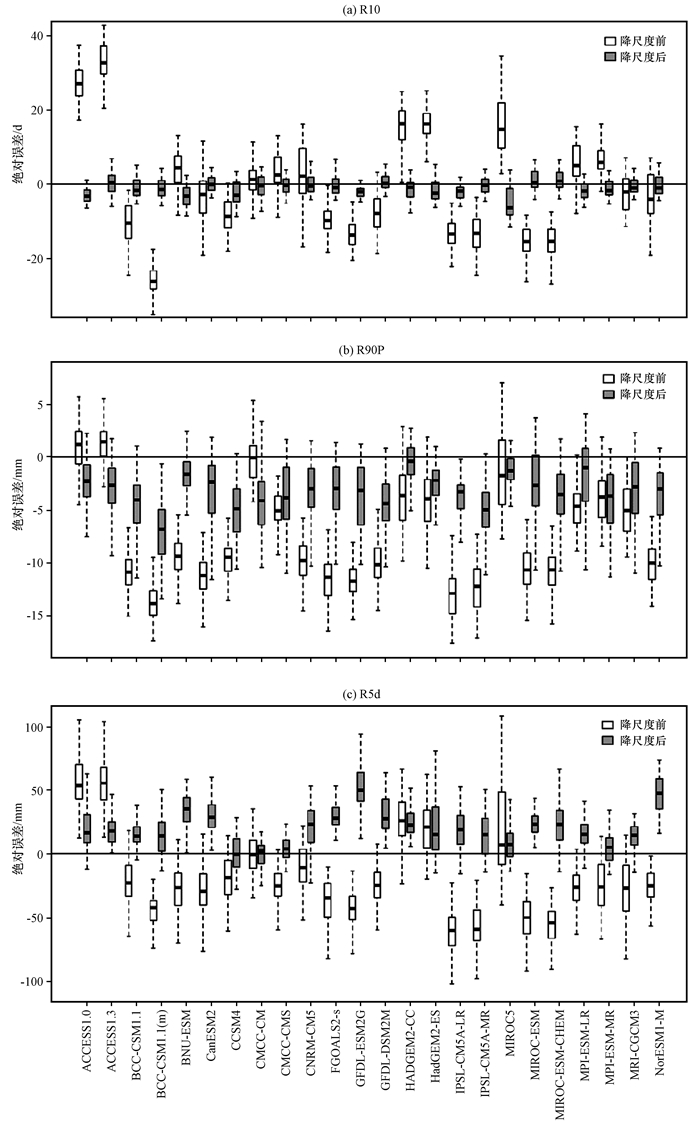
图 3 湖南地区各模式极端降水指数与观测之间绝对误差的盒须图 Fig. 3 The change in extreme precipitation indices for 24 models relative the observation over Hunan province

从图 3中可以看出, 总体来说, 降尺度以后模式模拟的R10、R90P和R5d三个极端降水指数与观测值的绝对误差与降尺度之前相比是偏小的。降尺度前, 模式模拟的R10与观测值的绝对误差偏大, 降尺度之后模式的绝对误差显著降低, 各模式的模拟结果与实况的绝对误差非常小。R90P降尺度前模式的模拟效果较差, 绝大部分模式偏差幅度超过8 mm。降尺度之后模式的绝对误差显著降低, 但是依然有较为显著的负偏差趋势, 所有模式绝对误差的中位数范围为0~8 mm, 不足之处在于模式空间差异的离散度增大。降尺度前, R5d显示模式模拟效果同样较差, 且与R90P一致表现为显著的负偏差, 大部分模式偏差幅度超过25 mm。降尺度之后模式的绝对误差显著降低, 且表现为较显著的正偏差趋势, 即降水偏多, 大部分模式偏差幅度在25 mm以内, 降尺度前后, 模式空间差异的离散度变化不大。

图 4给出了在降尺度前后24个模式集合的湖南地区极端降水各指数的空间分布与观测结果的对比。从图 4中可以看出, 对于R10, 24个模式集合的模拟效果与观测结果趋势上是一致的。在湘中、湘东和湘南等山区地区, 由于海拔较高, 受地形抬升等因素影响平均降水量和大雨日数偏多, 存在明显的大值区, 湘北平原区、湘西以及湘中衡邵盆地地势平坦, 受地形影响较小平均降水量和大于日数相对偏少。降尺度之前模式集合对R10的空间模拟效果较差, 虽然模拟结果大体呈现出了东部和中北部的大值区域, 但是空间差异较小, 未能再现R10变化的细节特征。与观测相比, 湖南地区空间平均绝对误差达到3.99天。降尺度后, R10的空间差异被较准确地模拟出来。与观测相比, 湖南地区空间平均绝对误差达到2.18天, 较降尺度前, 绝对误差降低了45.46%。从R90P实况分布看, 中北部为显著的大值区, 中心强度超过30 mm, 其次是东南部, 中心强度也在28 mm以上, 湘中衡邵盆地则表现为显著的低值区, 中心强度在25 mm以下。降尺度之前, 各模式集合结果显示出东高西低的分布特征, 但是空间差异较小, 不能反映R90P变化的细节特征。使用CDF-t统计降尺度后, 尽管空间差异得到体现, 但模拟效果不佳, 高、低值中心位置模拟与实况偏差较大, 尤其是对湘西中部R90P的模拟实况和降尺度以后的结果呈现相反的分布状态。这和泰勒图(图 2)的检验结果是一致的, CDF-t统计降尺度之后无论是相关系数还是均方根误差均和标准差等指标看都没有显著提高。从R5d实况和降尺度之后模式集合分布看, 两者的空间分布都是非常相似的, 大值区域分布在湘西南、湘西北、湘东和湘东等南地区, 湘中衡邵盆地则表现为显著的低值区。但降尺度之后各模式集合结果较实况略有偏高, 这和盒须图(图 3)的检验结果也是一致的。降尺度前, 各模式集合由于气候模式分辨率太低无法反映出R5d的分布特征, 但通过CDF-t统计方法降尺度之后的结果比较理想。对于R90P, CDF-t统计降尺度方法对于其空间结构特征模拟的改进效果则不是特别理想, 模式之间的差异较大, 大部分模式在降尺度之后未能模拟出R90P实况的空间模态和变化幅度。但是其中日本大气海洋研究所的模式MIROC5在降尺度处理之后能够表现出较好的模拟效果, 图 5为降尺度之后MIROC5模拟湖南1981—2005年R90P的空间分布。从图 5中可以看出, MIROC5模式经过降尺度处理之后, 成功模拟出实况中湘东北、湘中、湘西南以及湘东南的大值区, 相较于模式集合表现更为突出。但是极端气候变化模拟存在诸多不确定性, 多模式集合被认为能够有效减少上述不确定性, 其预估结果可靠性往往高于单个模式(周莉等, 2018; Palmer et al, 2005; Xu et al, 2010; 潘留杰等, 2017)。因此在即使降尺度后, 模式结果依然存在较大差异的情况下, 本文依然选用多模式集合的方法评估CDF-t统计降尺度对极端降水空间分布的模拟能力, 而非最优模式集合或模式加权平均。

图 4(Fig. 4)

图 4 验证时段湖南极端降水指数的空间分布 Fig. 4 The spatial pattern of extreme precipitation indices over Hunan province during validation periods

图 5(Fig. 5)

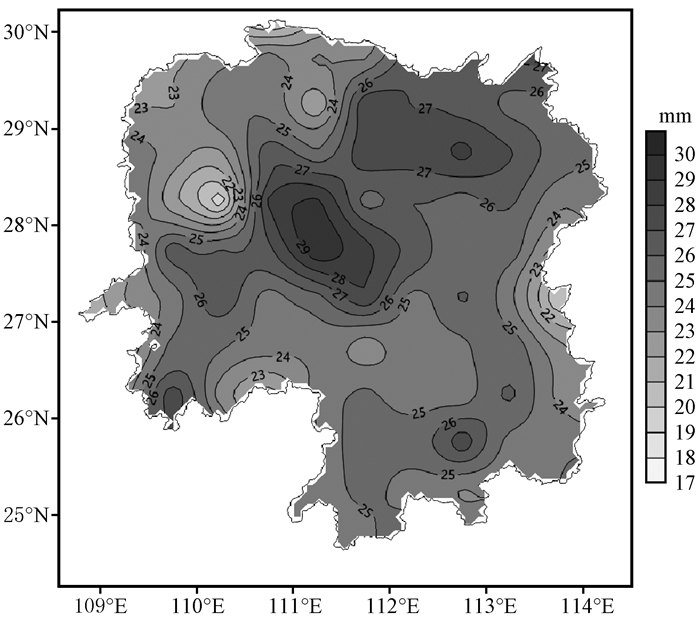
图 5 降尺度之后MIROC5模拟湖南验证时段R90P的空间分布(单位: mm) Fig. 5 The spatial pattern of R90P of MIROC5 with downscaling over Hunan province during validation period. Unit: mm

综上不难发现, 较低分辨率的CMIP5气候模式无法细致反映极端降水空间结构变化特征, 各模式之间也存在较大差异。CDF-t统计降尺度方法对于模式模拟湖南地区R10和R5d的空间结构能力都有很大改善, 且模式之间表现出较高的一致性, 尤其是R10。但该降尺度方法对于模式模拟R90P的空间结构能力没有得到有效提高。

由于极端降水在时间尺度上的变化对于灾害预警有着非常重要的现实意义, 因此检验CDF-t对气候模式模拟极端降水年际变率能力的改善程度是非常必要的。图 6为降尺度前后24个模式和模式集合平均(MME)IVS值的曲线图。从图 6中可以看出, 对于R10来说, 降尺度之后, 模式模拟时间变率的能力提高较小。只有近一半的模式在降尺度后有所改善, 从模式集合平均(MME)也不难发现, 降尺度前后MME的IVS值几乎是一致的。对于R90P和R5d来说, 降尺度之后, 模式模拟时间变率的能力显著提高。R90P降尺度前模式IVS值的范围为0.4~5.6, 经过降尺度处理之后IVS值显著减小, 范围降低至0.0~0.8之间。几乎所有模式的IVS值都有所降低, 其中法国的2个模式改善效果较为显著, 分别由降尺度前的5.6降低至0.1和0.4。从模式集合平均(MME)也不难发现, IVS值由降尺度前的2.2降低至0.3。R5d降尺度前模式IVS值的范围为0.3~5.5, 经过降尺度处理之后IVS值显著减小, 范围降低至0.2~1.0之间。绝大部分模式的IVS值都有所降低, 其中德国的模式MPI-EMS-MR改善效果较为显著, 由降尺度前的5.5降低至0.6。模式集合平均(MME)的IVS值由降尺度前的1.5降低至0.6。

图 6(Fig. 6)

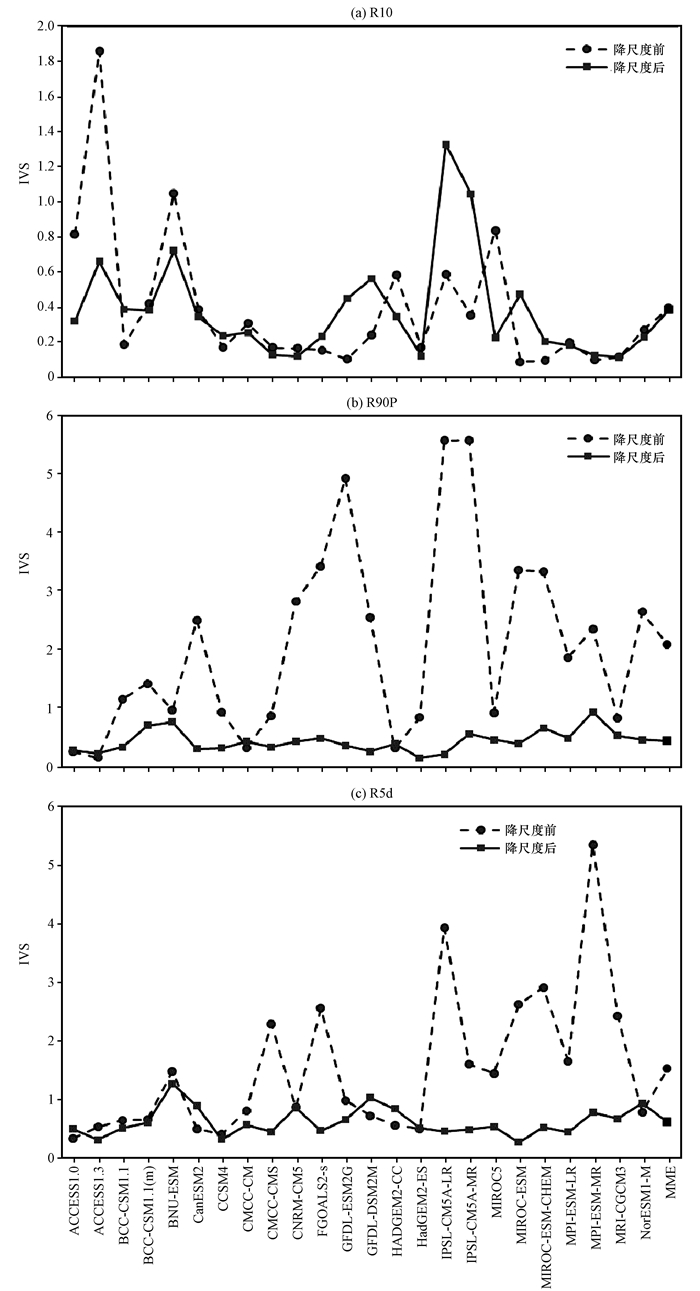
图 6 降尺度前后, 各模式以及多模式集合模拟湖南极端降水指数的IVS值 Fig. 6 The IVS simulated by the models before downscaling and after downscaling over Hunan province

从降尺度前后湖南多模式集合IVS的空间分布(图 7)可以看出, 对于R10的降尺度前多模式集合IVS的空间分布非常相似, 都存在一个明显的大值区, 位于湘西中部, 中心值都在1.3以上, 湘南地区IVS值较小, 在0.3以下。对比降尺度前多模式集合IVS的空间分布不难发现, 降尺度之后模式模拟时间变率的能力没有得到改善。对于R90P和R5d来说, 降尺度之后, 模式模拟时间变率的能力却是显著提高的。R90P降尺度前多模式集合IVS的空间分布自北向南呈高-低-高形势分布, 最大值区域位于湘北, 中心值达到6以上, 低值区域(小于1)位于湘中偏南。R5d降尺度前多模式集合IVS的空间场呈现北高南低的分布态势, 北部中心值达到1以上, 南部也超过0.2。而R90P和R5d降尺度之后多模式集合IVS整体大幅降低, 大部分地区都在0.2以下, 部分地区在0.2~0.4之间。可见对于R90P和R5d, CDF-t统计降尺度方法对于模式模拟其时间变率的能力有很大的改善, 这和降尺度前后多模式集合模拟湖南极端降水指数的区域平均IVS值(图 6)是一致的。

图 7(Fig. 7)

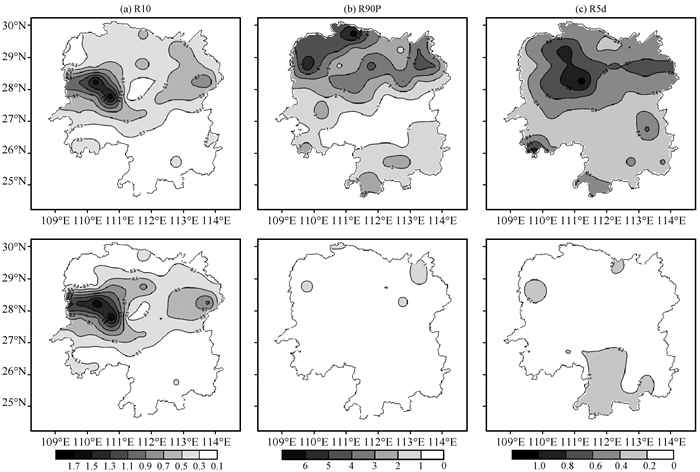
图 7 降尺度前(上)后(下)湖南多模式集合IVS的空间分布 Fig. 7 The spatial pattern of IVS for multi-models ensemble mean before downscaling (up) and after downscaling (down) over Hunan province

综上所述, 降尺度前的CMIP5模式, 无论是单个模式还是模式集合都无法细致反映湖南极端降水年际变率特征。CDF-t统计降尺度对于模式模拟整个湖南地区R90P和R5d的时间变率能力都有很大改善, 且模式之间表现出较高的一致性。降尺度之后模式模拟R10时间变率的能力没有得到提高。

利用CDF-t统计降尺度方法和24个CMIP5耦合模式的历史数据, 结合3个极端降水指数, 从空间结构和年际变率两方面评估降尺度前后CMIP5模式对湖南极端降水的模拟能力。得到以下主要结论:

(1) 有着较低分辨率的CMIP5气候模式无法细致而准确地反映区域极端降水变化特征, 各模式之间也存在较大差异, 大部分模式皆不能再现湖南极端降水的时空变化, 模式集合对其模拟效果相对较差。

(2) 综合评估CDF-t统计降尺度方法对3项极端降水空间结构的模拟能力, 发现降尺度方法对于模式模拟湖南地区R10和R5d的空间结构能力都有很大改善, 且模式之间表现出较高的一致性, 尤其是R10改善效果最显著, 与观测相比, 湖南地区空间平均绝对误差达到2.18天, 较降尺度前, 绝对误差降低了45.46%。

(3) 综合评估CDF-t统计降尺度方法对3项极端降水年际变率的模拟能力, 发现降尺度对于模式模拟整个湖南地区R90P和R5d的时间变率能力都有很大改善, 且模式之间表现出较高的一致性, 降尺度后IVS值分别由降尺度前的2.2和1.5降低至0.3和0.6。