2. 中山大学, 广东 广州 510275
山谷风是由于山坡上和坡前山谷中同一高度上的自由大气之间存在温差而形成的局地环流(寿绍文等, 2003)。由于山顶与谷底附近空气之间的热力差异, 在白天风从谷底吹向山顶, 产生谷风; 到夜晚, 风从山顶吹向谷底, 产生山风。山风和谷风总称为山谷风。山谷风可以认为是位于边界层内的一种周期为24 h的地方性风, 主要受复杂下垫面和地形的热力作用影响。由于下垫面受热不均, 近地面物质和能量通过湍流形式与大气进行交换, 导致区域性的气流辐合与辐散, 从而产生局地山谷风环流(Stull, 1988)。
近几十年, 对山谷风的研究广泛开展并取得一定成果(Stull, 1988; 邱崇践等, 1991; 李晓霞等, 2017; 欧阳琳等, 2017)。山谷风的早期研究主要是以观测为主要手段。Davidson et al (1963)从观测得到山谷风的演变特征。汤懋苍(1963)则利用祁连山区的观测资料对山谷风的日变化特征进行了描述。季国良等(1984)利用陕南某山区夏季的风场观测资料, 分析了山谷风的水平及垂直结构, 并讨论了其对污染物扩散的影响。林之光等(1985)则通过观测探讨了天山天池山谷风对局地温度与湿度日变化的影响。曹杨等(2017)则利用观测的多普勒声雷达风场资料和探空资料证实了邢台市皇寺近地面山谷风的存在。随着数值模式的出现与发展, 也有不少学者对山谷风进行了数值试验。蒲朝霞等(1991)利用一个二维小尺度数值模式对兰州地区的山谷风环流进行数值模拟, 得到与观测较为接近的结果。邱崇践等(1991)则利用该模式研究了山谷风环流控制下的大气污染输送和扩散过程。席世平等(2007)利用中尺度数值模式MM5对河南省西部山区的山谷风进行了数值模拟, 证实了地形热力作用对山谷风形成的重要作用。许鲁君等(2014)利用耦合了湖泊模型的WRF_CLM模式模拟了大理苍山—洱海地区的局地环流, 再现了该地区山谷风与湖陆风相互作用的局地环流特征。这些研究大都采用传统中尺度数值模式, 并通过参数化方案刻画复杂地形对山谷风形成的动力热力影响, 对山谷风的特征进行一般描述。
近些年, 随着超级计算机的发展以及计算流体力学(CFD)在气象研究中的应用, 不少学者采用CFD模式, 如大涡模拟(LES)进行高精度数值试验。大涡模拟能显式表征复杂陡峭的地形, 对网格尺度的湍流及动力热力作用进行直接刻画, 因而能从更加精细的角度对山谷风的形成进行研究。Catalano et al (2010)利用WRF模式和一个次网格尺度湍流方案对理想山谷中的环流进行了大涡模拟, 探讨了山谷中湍流、边界层结构以及山谷风环流的不同特征。Serafin et al (2010)则采用一个大涡模式(ARPS)对一个二维理想的山谷进行了高分辨率的数值模拟, 研究了白天山谷中热量传输以及湍流对山谷风环流的影响。
重庆位于中国西南部、长江上游地区, 为青藏高原与长江中下游平原的过渡地带, 是典型的山地型城市(程炳岩等, 2012)。辖区内山河众多, 地势沿山脉、河流起伏, 构成以山地、丘陵为主的地表形态。这种复杂地形势必会产生局地热力差异, 而这种差异是否能在重庆本地形成山谷风, 若能, 其对重庆天气气候的影响又有什么样的影响。目前, 对这些问题的研究还比较少。本文利用大涡模拟手段, 针对重庆实际的复杂地形, 结合较为理想的初始条件, 对局地山谷风环流进行高精度数值模拟, 分析局地山谷风环流的基本特征, 并初步探讨因复杂地形而产生的局地热力差异对山谷风形成的影响。这在一定程度上有助于提高对复杂地形下城市局地环流场的科学认知, 同时为面向城市规划等的气象服务工作提供一定的理论支撑。
2 模式和资料 2.1 模式介绍所用到的CFD模式是日本东北大学基于大涡模拟开发的一个局地气象模式(Sha, 2002)。表 1给出了该模式的具体参数。该模式基于三维笛卡尔坐标, 能显式分辨陡峭的地形以及城市中的建筑物, 采用Blocking-off手段来处理复杂的下垫面几何形状。模式采用完全可压的Navier-Stokes方程组, 采用有限元方法离散, 同时利用压力速度耦合SIMPLER方法(Patankar, 1980)进行求解。模式在每个积分步长中反复迭代至收敛, 以保证各要素的物理一致性。方程平流方案采用的是三阶QUICK方案(Leonard, 1979), 时间积分采用完全隐式方案。次网格湍流的处理则是采用Lilly-Smagorinsky大涡模拟模型(Lily, 1962; Smagorinsky, 1963)。该局地模式为干模式, 不包含湿过程和辐射过程。详细模式介绍请参考Sha (2008)的文献。
| 表 1 CFD模式参数 Table 1 Description of the CFD model |
Chen et al(2015a, 2015b)和Jiang et al(2017)利用该模式对复杂下垫面上的具有明显密度差异的天气过程(大气重力流)进行了一系列的数值试验, 指出该模式能够很好的展现复杂下垫面对局地精细化环流场的热力动力影响。因此, 本文采用该模式对复杂地形下具有温度(密度)差异的局地山谷风环流进行数值模拟。
2.2 资料CFD模式所需的地形资料采用的是航天飞机雷达地形测绘任务(SRTM)分辨率为90 m的数值高程数据4.1版本(Jarvis et al, 2008)。该资料水平分辨率为90 m, 使用前采用双线性插值方法插值到30 m分辨率, 备CFD模式使用。
本文采用较为理想的初始条件探讨因复杂地形而导致的热力差异对山谷风环流形成的影响。模式的设置以及初、边界场需满足基本的物理规律。这里以基于地面站点观测资料的理想初始场来驱动CFD模式, 选取的两个站点分别为沙坪坝站(57516)和中梁站(A8003)。其中沙坪坝站为国家气象站, 而中梁站为区域气象站, 两站的具体信息见表 2。两站观测资料的时间分辨率为逐小时, 所用到的气象要素包括气压、风场和温度。
| 表 2 气象站点的详细信息 Table 2 Details of surface meteorological stations |
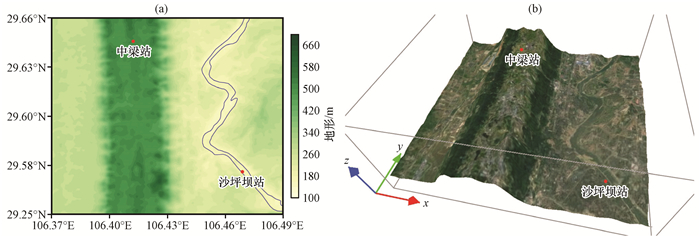
选取的研究区域主要位于重庆沙坪坝区, 包括中部偏东的沙坪坝老城区、中部偏西南北走向的中梁山、嘉陵江东岸的江北部分区域以及区域西部的西永片区。区域具体的经纬度范围为29.553°N—29.656°N, 106.366°E—106.487°E, 大小约为11 km×11 km。区域地形平面图见图 1(a), 卫星遥感影像及其三维视图见图 1(b)。研究区域地形基本呈现南北向带状分布, 即南北向的地形高度差异很小。地形在东西方向上表现为“低—高—低”的形态, 西边海拔在300 m左右; 中部靠西东西向约3 km的范围内为中梁山脉, 海拔在600 m左右; 东部则为嘉陵江河谷平坝区, 海拔在240 m左右。这种南北向分布均匀的地形, 若只考虑不同海拔处下垫面的热力差异而忽略其他影响因素, 则可得到南北向均匀的环流场, 比较适宜简单的理想试验研究。
|
图 1 研究区域平面视图(a, 彩色区, 单位: m)和卫星遥感影像的三维视图(b) (a)中蓝色线条代表嘉陵江所在位置 Fig. 1 Plain view (a, color area, unit: m) and three-dimensional view of satellite remote sensingimage (b) of CFD model domain. Blue lines in Fig. 1(a) represent Jialing River |
本文使用的大涡模式利用有限元方法离散方程、采用完全隐式时间积分方案, 同时利用壁面函数处理壁面条件, 因此采用规则的结构网格进行模式网格划分。坐标为局地直角坐标系, x、y、z分别为纬向、经向和垂直方向。水平分辨率为30 m, 垂直方向分辨率在600 m以下为30 m, 600 m以上格距以1.09倍的速率递增。总的格点数为390×390×50。模式层顶高度约为4 km, 考虑到山谷风环流基本位于边界层内, 伸展高度不高, 这里的设置完全满足试验要求。
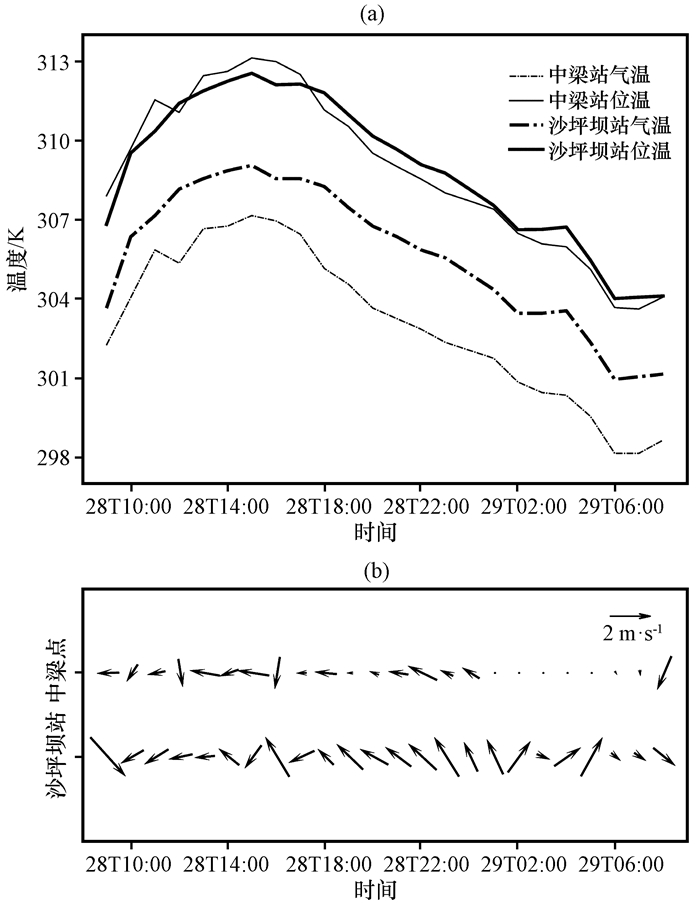
3.2 沙坪坝山谷风的观测事实为了考察研究区域内是否存在局地山谷风环流, 普查区域内沙坪坝站和中梁站从2017年1月1日至12月31日的所有逐时观测资料, 同时剔除含有明显天气过程(如降水)的时间段, 最终选取2017年8月28日09 : 00(北京时, 下同)至29日08 : 00作为研究个例, 进行详细分析。图 2(a)虚线给出了两个气象站气温的逐时演变。两站气温表现为明显的日变化, 即28日日出后(09 : 00)随着地面加热气温逐渐升高, 到午后(16 : 00)达到最高, 之后逐渐降低, 直至29日凌晨(06 : 00)。中梁站位于中梁山上, 海拔为511.5 m, 而沙坪坝站位于嘉陵江畔, 海拔只有259.1 m(图 1, 表 2)。两者海拔落差达到252.4 m, 因此中梁站的气温明显低于沙坪坝的气温。两者差值在1~3 ℃之间, 由此可以推算出气温垂直递减率在0.4~1.2 ℃·(100 m)-1内变化, 其与对流层内气温的平均垂直递减率0.6 ℃·(100 m)-1相接近。
|
图 2 2017年8月28日09 : 00至29日08 : 00气象站观测的温度(a)和风场(b, 单位: m·s-1)的逐时演变 Fig. 2 Time evolution of temperature (a) and wind field (b, unit: m·s-1) from 09 : 00 on 28 to 08 : 00 on 29 August 2017 |
由于山谷风是山坡和坡前山谷中同一高度上的自由大气之间存在温差而形成的局地环流, 因此需要将不同海拔高度处的两站气温换算成位温来考察两站的温差。位温的换算公式为
| $ \theta=T\left(\frac{P_{s}}{P}\right)^{0.286}, $ | (1) |
式中: Ps为海平面气压; P为本站气压(单位: hPa); T为本站气温(单位: K)。根据沙坪坝站观测到的气压、气温, 可换算出沙坪坝站的位温。中梁站为区域站, 不含气压观测, 不能直接计算其位温。这里利用压高公式, 并根据沙坪坝站与中梁站的海拔落差以及沙坪坝站的气压和气温数据计算沙坪坝站的高空气压, 并用其近似代表中梁站在同高度处的气压, 最后再计算中梁站的位温。其计算结果如图 2(a)实线所示。两地在海平面处的温度(即位温)存在明显差异, 且两者的差异随时间发生变化。特别地, 在28日日出后(09 : 00)至傍晚(18 : 00), 中梁站的位温比沙坪坝站高, 即中梁站所在位置的空气比相同高度处的沙坪坝站的空气暖, 这种气温差异能在水平方向上产生气压梯度力, 导致风从中梁山下的沙坪坝站吹向山上的中梁站, 即形成谷风。这种温度差异在28日傍晚(18 : 00)至29日日出前(08 : 00)反转, 因此在这个时间段内有可能形成山风。
为了证实这种猜想, 考察沙坪坝站和中梁站观测到的水平风场的逐时演变, 结果如图 2(b)。在28日10 : 00至29日02 : 00, 沙坪坝站的近地面风场均存在明显的东风分量, 即有风从中梁山的山谷吹向山坡。随后, 沙坪坝站的风场顺转, 变为西风, 即远离中梁山。这种风场的分布与两站的温度差异虽然不能一一匹配, 但情况大致相符, 即白天吹谷风晚上吹山风。至于风与温度不匹配, 很有可能和其他原因如较大尺度的背景环流场有关。
3.3 山谷风理想试验设置气象站逐时资料的分析表明某些特定天气条件下研究区域内能出现山谷风环流。基于此, 本文设计山谷风理想试验, 探讨下垫面热力状况对局地山谷风形成的作用。其基本思路是:考虑一种理想的初始情况, 即静风状态, 然后用观测的气温和实际的地形来驱动模式, 从而得到仅仅由不同的热力状况强迫出来的山谷风环流, 由此分析下垫面对山谷风环流的热力影响。
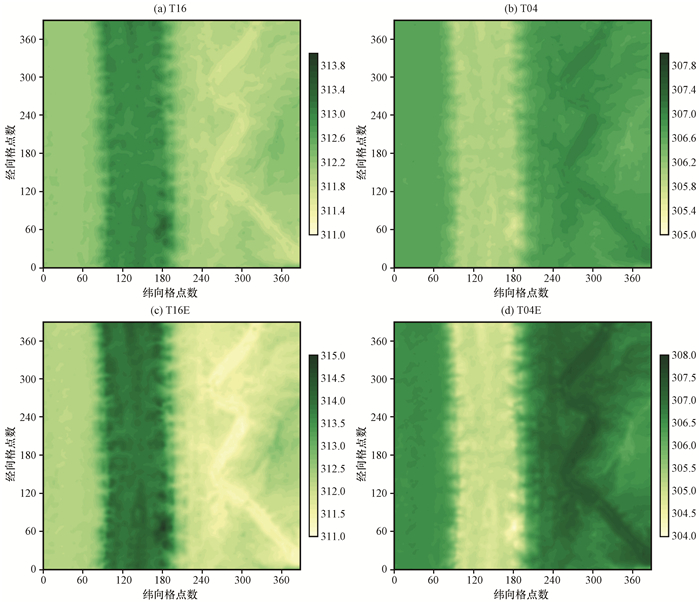
这里选取地面观测时间段内出现显著山风和谷风环流的时间点, 即28日16 : 00和29日04 : 00, 作为主要研究时间, 设计两组试验T16和T04, 分别代表白天的谷风和夜晚的山风。这两组试验中所观测到的沙坪坝和中梁山的位温分别为312.09 K、312.98 K和306.72 K、305.98 K(表 3)。在数值试验中, 由于需要考虑不同地形高度处地面和空气不同的热力状况, 因此必须给定温度场的三维分布。而目前所拥有的资料仅仅为两个站点的近地面气温, 因此需要通过一定的手段将其插值到三维场中。考虑一种较为简单且理想的情况, 假设区域内近地面气温随地形高度线性变化。根据两个观测站点观测到的气温和他们所在的海拔即可换算出整个区域近地面气温的分布。T16和T04试验中计算所得到的近地面气温的空间分布见图 3(a)~(b)。理所当然地, 其分布形与地形[图 1(a)]的分布基本一致。
| 表 3 不同山谷风理想试验中两个观测站处的位温设置 Table 3 Configurations of potential temperatures in different CFD-model simulations |
|
图 3 不同CFD模式试验位温的空间分布(单位: K) Fig. 3 Spatial distribution of potential temperatures in different CFD-model simulations. Unit: K |
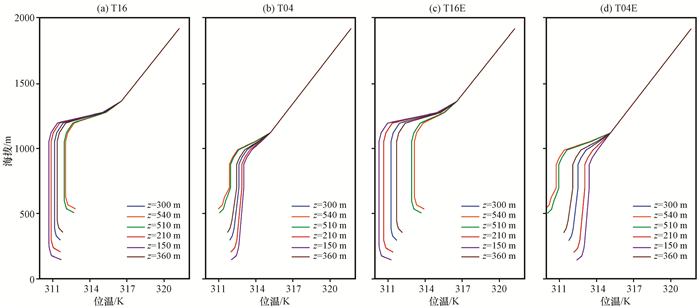
由于研究区域内缺少气温的廓线观测, 因此只能人为给定位温的垂直分布, 但需与实际情况相接近。这里从谷风和山风两种不同的情况进行讨论。谷风试验(T16)的发生时间在16 : 00, 此时下垫面受太阳辐射升温, 边界层处于不稳定状态, 且能伸展到较高层次。据此设置不同海拔处的位温廓线, 如图 4(a)(仅给出部分廓线), 并做了几个设定:边界层整体为弱不稳定状态, 且近地面附近有明显加热; 边界层高度统一设置为1.2 km。这种设置接近白天边界层的加热状况。由于不同海拔高度处地表温度(近地面气温)与较高层次气温存在差异, 所以在经过一定时间的积分后, 大涡模式能产生仅仅由热力驱动的风场。而山风试验(T04)则发生在04 : 00, 此时下垫面辐射冷却, 其上部边界层处于完全稳定状态, 边界层厚度也较薄。该试验设定的边界层整体为稳定状态, 近地面附近有明显冷却; 边界层高度设置为900 m[图 4(b)]。这种设置也接近于晚上边界层的冷却状况。
|
图 4 不同CFD模式试验位温的垂直廓线 Fig. 4 Potential temperature profiles of different CFD-model simulations |
上述模式初始场基于沙坪坝站和中梁站的实际观测。为了研究下垫面热力差异对山谷风环流形成的影响, 在理想试验中, 可以根据某些特定条件进行敏感性试验。比如, 在白天受某些天气系统或其他现象的影响, 山坡的气温升温比山谷快很多, 即山坡山谷温相差较大, 此时山谷风环流会出现怎样的变化?为了解决诸如此类的问题, 可以在模式中人为地扩大山坡和山谷(即沙坪坝站和中梁站)的温差, 设置敏感性试验。晚上的山风类似。作为其中的一种情况, 将两站的温差扩大近一倍, 即设置试验T16E和T04E, 研究具有明显温差情况下山谷风环流强度的变化特征。试验位温的具体设置见表 3, 试验近地面温度的空间分布和位温廓线分别见图 3(c)~(d)和图 4(c)~(d)。
四组试验均模拟1 h, 积分步长为1 s。对模式输出相关扰动通量(图略)的分析结果表明, 区域内三维流场在积分30 min之后均能达到准稳定的状态(不同试验达到准稳态的时间不同), 故下文环流场的分析均基于模式在t = 30 min时的瞬时输出。
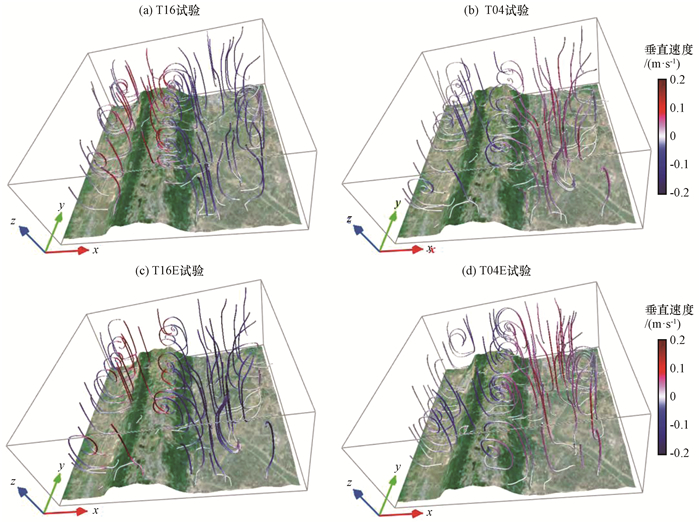
4 沙坪坝山谷风理想试验结果 4.1 控制试验(T16和T04)的模拟结果首先分析控制试验(T16和T04)的模拟结果。T16试验采用基于地面观测站28日16 : 00数据的理想三维温度场驱动CFD模式。模式输出的三维环流场[图 5(a)]表明, 研究区域内的整体流场在南北方向上分布比较一致, 但在东西方向差异较大。这主要与地形以及和地形相关的初始温度场的分布有关。区域内的垂直流线从西到东分别表现为较为规则逆时针和顺时针环流。对应地, 在区域西部和东部海拔较低的区域为明显的下沉运动; 而在地势较高的中梁山脊附近则为强盛的上升运动。因而在白天受区域内不均匀加热的影响, 在近地面会形成由地势较低的西部和东部吹向地势较高的中部的谷风。与T16试验相同, T04试验的垂直环流也具有经向上的分布均匀、纬向上存在较大差异的特征[图 5(b)]。T04试验的垂直环流的方向与T16试验相反, 即在西部和东部海拔较低的区域为明显的上升运动; 而在地势较高的中梁山脊附近则为强盛的下沉运动。这表明, 在午夜受区域内不均匀冷却的影响, 在近地面会形成由中部地势较高的中梁山吹向地势较低的西部和东部的山风。
|
图 5 不同CFD模式理想试验结果的三维视图 线条为流线, 其颜色代表垂直速度(单位: m·s-1) Fig. 5 Three-dimensional view of different CFD-model simulations. The lines are streamlines, and the colors indicate vertical velocity (unit: m·s-1) |
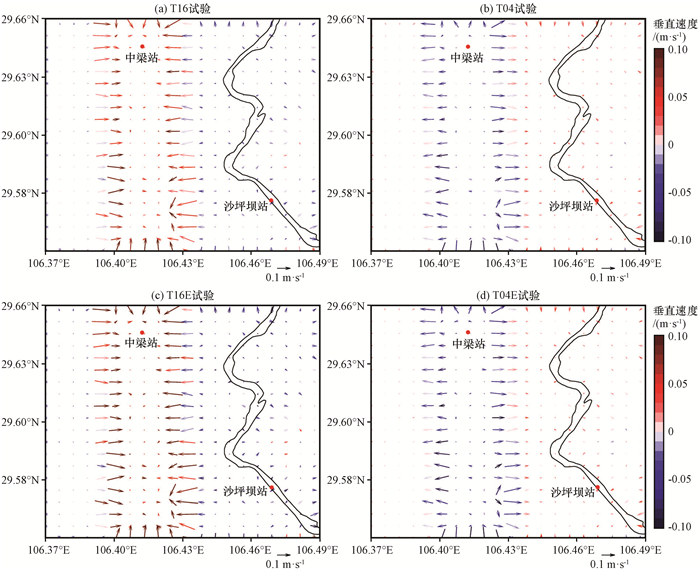
为了进一步研究控制试验中山谷风的近地面特征, 对离地30 m高度处(30 m AGL)的风场进行分析。图 6(a)显示了T16试验中一个非常明显的特征, 在区域内坡度最大的中梁山山脊两侧(即经度在106.39°E和106.43°E附近)存在量级较大的水平风和上升运动。风速数值在0.15 m·s-1左右, 风向都主要由东西两侧指向山脊。这表明在山脊两侧的斜坡上存在明显的谷风。但在中梁山山坡上, 虽然也存在量级相当的垂直运动, 但却没有出现风速较大的水平风, 即在山坡较为平坦的地方并没有明显的谷风出现。而这种谷风的在山坡和山脊处的差异在之前的较大尺度的数值研究中并没有被揭示。在海拔较低的东部和西部, 主要由下沉运动控制, 水平风较小且风向比较散乱。这与区域内局地的地形起伏有关。另外, 在研究区域四周出现了风场与周围不一致的情况, 这主要是由模式的边界效应导致。模式在中梁站和沙坪坝站两个观测点附近模拟的风向和风速分别为东南风0.02 m·s-1和东北风0.05 m·s-1, 与观测值有一定差异。这是由于模式的初始场设置为理想条件, 仅仅只考虑了地形热力和动力对山谷风环流的影响, 但是实际的近地面风场不仅仅受局地环流的影响, 还受到较大尺度的天气过程的控制, 因此两者存在差异。
|
图 6 不同CFD模式理想试验离地30 m高度处的风场(矢量, 单位: m·s-1) 矢量颜色表示垂直速度(单位: m·s-1) Fig. 6 Near-surface winds (vector) in different CFD-model simulations. Unit: m·s-1. The colors indicate the vertical velocity (unit: m·s-1) |
图 6(b)显示的是T04试验的近地面风场。近地面风速仍然是在坡度较大的中梁山山脊两侧最大(0.1 m·s-1), 且伴随着强烈的下沉运动(量级为-0.01 m·s-1)。这表明04 : 00, 山脊的两侧的斜坡上存在明显的由中梁山坡吹向中梁山谷的山风。在中梁山山坡上较为平坦的区域却难以看到风速较大的水平风。这表明, 在山脊处并没有明显的山风出现, 整个山顶区域基本为静风状态。在海拔较低的东部和西部, 则主要由上升运动控制, 但同T16试验一样, 受局地地形起伏的影响, 水平风场风速较小且方向比较散乱。模式在中梁站和沙坪坝站两个观测点附近模拟的风向和风速分别为西北风0.02 m·s-1和西南风0.05 m·s-1, 与观测也相差较大。
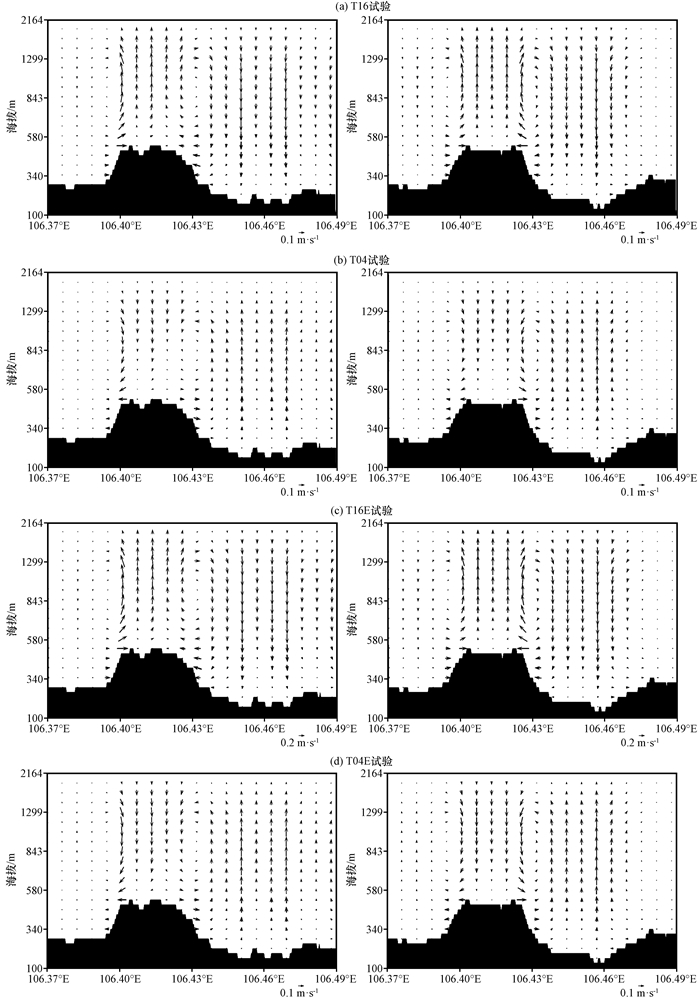
本节分析控制试验的垂直环流, 探讨理想山谷风在边界层内的特征。图 7(a)显示了T16谷风试验中沿不同纬度的垂直环流。在不同纬度上, 谷风垂直环流场的分布基本一致。在中梁山山脊两侧存在明显吹向山顶的斜坡风, 但在山坡较为平坦和海拔较低的区域, 近地面风场则较弱(与上文一致)。另外, 在中梁山山脊两侧的高空处存在明显的逆时针和顺时针的垂直环流, 且垂直环流的伸展高度能达到1.2 km左右, 该高度与设置的边界层高度较为一致。但在中梁山山坡上的垂直运动却能突破边界层, 达到2 km以上的高度, 这与该处因地表加热而产生的强烈对流有关。T04试验的垂直环流[图 7(b)]在中梁山两侧也存在明显的斜坡风, 但方向与T16相反, 即产生明显的山风。同时, T04整个垂直环流的伸展高度只有不到1 km, 这可能与边界层较为稳定的状态有关。
|
图 7 沿29.59°N(左)和29.62°N(右)垂直风场的经度—高度剖面(矢量, 单位: m·s-1) 灰色阴影为地形 Fig. 7 The wind field (vector) of the x- zcross sections along 29.59°N (left) and 29.62° (right) in different CFD-model simulations. Unit: m·s-1. The grey shades indicate topography |
本文设置的两个敏感性试验(T16E和T04E)主要扩大了山坡与山谷的温差, 用以考察下垫面受热差异程度对山谷风环流强度的影响。T16E试验结果的三维视图[图 5(c)]以及30 m AGL风场[图 6(c)]与T16试验基本一致, 但环流的强度有所增强。T16E近地面谷风风速可以达到0.3 m·s-1, 对应的垂直风速能达到0.1 m·s-1。在地势较低的中梁山东侧, 下沉运动也比T16强。从剖面图[图 7(c)]中的垂直环流也可以看到, 斜坡上的全风速可达0.4 m·s-1, 明显比T16大, 且山坡上的上升运动也很强, 且能伸展到比T16试验更高的层次(~1.5 km)。由此可以推断, 在白天受某些因素的影响, 山坡升温比山谷快, 两者温度差异扩大, 山坡(山谷)存在更强的上升(下沉)运动, 且对应的斜坡上的谷风也更强。T04E山风敏感性试验的表现与T16E不尽相同。CFD模式模拟的三维流场[图 5(d)]、近地面风场[图 6(d)]以及垂直剖面图[图 7(d)]与T04试验基本一致, 且强度也大致相同。就理论上讲, 若扩大晚上山坡与山谷的温度差异, 形成的山风环流应该更为强盛。但是, 模式模拟的结果显示两者并没有明显差异。这表明, 在晚上即使增加山顶和山脚温度差异, 也不能使山风环流的强度明显增加。
5 结论和讨论重庆高低起伏的地形在同一高度处会产生明显的热力差异, 这种差异则会进一步导致山谷风环流的形成, 从而对局地的天气气候产生影响。本文选取重庆沙坪坝区中梁山—嘉陵江一带作为研究区域, 利用大涡模拟手段, 结合基于气象站观测事实并理想化的初始条件, 对局地山谷风环流进行高精度数值模拟, 探讨热力差异对局地山谷风环流形成的影响。结果表明:
(1) 仅仅由复杂地形导致的局地热力差异能够在局地形成山谷风环流。在白天(T16)受太阳辐射作用, 山坡升温幅度比山谷明显, 在同一海拔处形成温度差异, 形成明显的谷风环流。谷风环流最明显的位置是在山脊两侧坡度较大的地方, 在山坡和山谷地势较为平坦的区域表现并不显著。在凌晨(T04), 山谷的保温作用明显, 而山坡辐射冷却较强, 产生由山坡吹向山谷的山风环流。山风环流的特征与谷风基本一致, 但垂直环流方向相反。本文考察的仅仅是由热力差异驱动的山谷风环流, 虽然理想山谷风的一般特征与观测较为接近, 但强度却存在差异。模式模拟的斜坡风的仅有0.1 m·s-1。
(2) 扩大山顶与山脚热力差异的幅度能调节局地山谷风环流的强度。当不同海拔处受热差异扩大时, 白天的谷风环流有明显增强, 理想的斜坡风能增大到0.4 m·s-1, 对应的上升运动以及边界层高度均有所增加; 而晚上的山风环流增强并不明显, 对应的斜坡风、上升运动以及边界层高度均与控制试验接近。
本文设计了一系列较为理想的数值试验, 关注的重点是因地形高低起伏导致的热力差异对局地山谷风形成的影响, 并没有考虑中尺度天气及其他过程对局地风场的调节作用。因此后续的研究需要采用更多精准的资料, 同时结合中尺度数值模式, 利用降尺度数值模拟方法对局地山谷风环流进行实际天气过程的数值模拟。
Catalano F, Moeng C H. 2010. Large-eddy simulation of the daytime boundary layer in an idealized valley using the weather research and forecasting numerical model[J]. Boundary-Layer Meteorology, 137: 49–75.
DOI:10.1007/s10546-010-9518-8 |
|
Chen G, Zhu X, Sha W, et al. 2015a. Toward improved forecasts of sea-breeze horizontal convective rolls at super high resolutions[J]. Part Ⅰ:Configuration and verification of a down-scaling simulation system (DS3)[J]. Monthly Weather Review, 143: 1849–1872.
DOI:10.1175/MWR-D-14-00212.1 |
|
Chen G, Zhu X, Sha W, et al. 2015b. Toward improved forecasts of sea-breeze horizontal convective rolls at super high resolutions[J]. Part Ⅱ:The impacts of land use and buildings[J]. Monthly Weather Review, 143: 1873–1894.
DOI:10.1175/MWR-D-14-00230.1 |
|
Davidson B, Rao P K. 1963. Experimental studies of the valley-plain wind[J]. Air and Water Pollution, 7(9/10): 907–923.
|
|
Jarvis A, Reuter H I, Nelson A, et al, 2008. Hole-filled SRTM for the globe Version 4[DB/OL]. Available from the CGIAR-CSI SRTM 90 m Database. http://srtm.csi.cgiar.org.
|
|
Jiang P, Wen Z, Sha W, et al. 2017. Interaction between turbulent flow and sea breeze front over urban-like coast in large-eddy simulation[J]. Journal of Geophysical Research-Atmospheres, 122.
DOI:10.1002/2016JD026247 |
|
Leonard B P. 1979. A stable and accurate convection modeling procedure based on quadratic upstream interpolation[J]. Computer Methods in Applied Mechanics and Engineering, 19(1): 59–98.
DOI:10.1016/0045-7825(79)90034-3 |
|
Lilly D K. 1962. On the numerical simulation of buoyant convection[J]. Tellus, 14(2): 148–172.
DOI:10.1111/j.2153-3490.1962.tb00128.x |
|
Patankar S V. 1980. Numerical heat transfer and fluid flow[M]. Taylor & Francis Press, 214.
|
|
Serafin S, Zardi D. 2010. Daytime heat transfer processes related to slope flows and turbulent convection in an idealized mountain valley[J]. Journal of the Atmospheric Sciences, 67(11): 3739–3756.
DOI:10.1175/2010JAS3428.1 |
|
Sha W. 2002. Design of the dynamics core for a new-generation numerical model of the local meteorology (in Japanese)[J]. Kaiyo Monthly, 2: 107–112.
|
|
Sha W. 2008. Local meteorological model based on LES over the Cartesian coordinate and complex surface (in Japanese)[M]. Meteorological Society of Japan Press, 21-26.
|
|
Smagorinsky J. 1963. General circulation experiments with the primitive equations[J]. Monthly Weather Review, 91(3): 99–164.
DOI:10.1175/1520-0493(1963)091<0099:GCEWTP>2.3.CO;2 |
|
Stull R B. 1988. An introduction to boundary layer meteorology[M]. Dordrecht: Kluwer Academic Publishers, 666.
|
|
曹杨, 陈洪滨, 王普才. 2017. 声雷达资料可靠性及近地面边界层风场特征分析[J]. 高原气象, 36(5): 1315–1324.
DOI:10.7522/j.issn.1000-0534.2016.00100 |
|
程炳岩, 李永华, 唐红玉, 等. 2012. 重庆市气候业务技术手册[M]. 北京: 气象出版社, 275.
|
|
季国良, 张礼才, 邢连壁, 等. 1984. 山谷风与山区污染物的扩散[J]. 环境研究, 2: 10–15.
|
|
李晓霞, 黄涛, 王兴, 等. 2017. 兰州新区近地层风场时空特征分析[J]. 高原气象, 36(4): 1001–1009.
DOI:10.7522/j.issn.1000-0534.2016.00092 |
|
林之光, 李映江. 1985. 天山天池山谷风的气候研究[J]. 地理研究, 4(1): 63–70.
DOI:10.11821/yj1985010007 |
|
欧阳琳, 阳坤, 秦军, 等. 2017. 喜马拉雅山区降水研究进展与展望[J]. 高原气象, 36(5): 1165–1175.
DOI:10.7522/j.issn.1000-0534.2016.00111 |
|
蒲朝霞, 邱崇践. 1991. 兰州地区山谷风环流的二维数值模拟[J]. 兰州大学学报(自然科学版), 27(2): 169–175.
DOI:10.3321/j.issn:0455-2059.1991.02.032 |
|
邱崇践, 蒲朝霞. 1991. 山谷风环流控制下的大气污染物输送和扩散过程:二维数值模拟研究[J]. 高原气象, 10(4): 362–370.
|
|
寿绍文, 励申申, 姚秀萍. 2003. 中尺度气象学[M]. 北京: 气象出版社, 329.
|
|
汤懋苍. 1963. 祁连山区天气的日变化[J]. 地理学报, 30(3): 197–206.
DOI:10.11821/xb196303003 |
|
席世平, 寿绍文, 郑世林, 等. 2007. 复杂地形下山谷风的数值模拟[J]. 气象与环境科学, 30(3): 41–44.
DOI:10.3969/j.issn.1673-7148.2007.03.009 |
|
许鲁君, 刘辉志, 曹杰. 2014. 大理苍山-洱海局地环流的数值模拟[J]. 大气科学, 38(6): 1198–1210.
DOI:10.3878/j.issn.1006-9895.1401.13293 |
2. Sun Yat-sen University, Guangzhou 510275, Guangdong, China
 2019, Vol. 38
2019, Vol. 38
