2. 中国科学院青藏高原地球科学卓越创新中心, 北京 100101;
3. 中国科学院大学, 北京 100049;
4. 中山大学大气科学学院, 广东 广州 510275;
5. 中国科学院青藏高原研究所, 北京 100101;
6. 成都市气象局, 四川 成都 610071
青藏高原面积占中国陆地面积四分之一, 平均海拔在4000 m以上, 其复杂地形和高海拔产生的热力作用使得春夏季的青藏高原成为北半球大陆同纬度的一个强大的地面热源, 强力的动热力作用对青藏高原及其邻近地区独特的天气现象和气候背景有着巨大的影响, 对亚洲季风的形成和全球大气环流的布局也有着重要的贡献。研究表明, 青藏高原地面加热场强度的变化通过影响环流场, 进而影响西北降水, 从而导致我国西北地区干旱的发生(李栋梁等, 1990; 周俊前等, 2016); 高原地表热异常通过强迫500 hPa东亚大气环流来影响四川盆地降水(陈忠明等, 2003; 梁玲等, 2013); Yanai et al(1992)最早提出青藏高原近地层大气加热使得对流层成为一暖中心, 这个暖中心的温度平流可以影响南海夏季风爆发; 张艳等(2002)指出高原不同地区的感热加热分布造成高原和南方的温度梯度存在着不同的反转时间, 从而导致亚洲各区域夏季风的建立时间存在差异; 青藏高原热力作用不仅对亚洲季风和降水变率有着重要影响, 而且还通过激发类似于亚洲—太平洋涛动的大尺度遥相关, 影响着北美和欧洲以及南印度洋的大气环流和气候(周秀骥等, 2009)。总之, 准确的估算青藏高原地面热源强度的组分构成和配置关系对于更深入地了解和分析其地气相互作用过程具有重要的意义。
地面热源由两部分组成, 即感热通量和潜热通量。感热通量受风速和地气温差变化的影响, 潜热通量受降水或土壤湿度变化的影响。不同方法计算的湍流通量特征具有明显差异(严晓强等, 2018), 目前关于地面感热通量、潜热通量的观测计算方法主要包括直接法(主要是涡动相关法)和间接法(主要有空气动力学法、波文比法、空气动力学组合法以及总体输送法等)。当前应用最多的是基于半经验的莫宁-奥布霍夫(Monin-Obukhov)相似性函数的空气动力学法(Aerodynamic Method, AM), 它利用两层以上的风温湿梯度观测数据计算湍流通量, 结果有较好的稳定性, 但由于该方法函数的参数化方案较多且不统一, 所以使湍流通量的计算结果不确定性较大(Dyer et al, 1974; Yaglom, 1977; 刘树华等, 1995); 涡动相关法(Eddy Covariance, EC)是通过超声风、温仪和气体分析仪观测的高频三维风速以及空气温度和水汽脉动资料, 通过协相关分析直接计算湍流通量, 是目前认为精度较高最接近湍流实际情况的直接测量方法, 其观测计算得到的感热通量、潜热通量的值相较于通过其他方法计算得到的感热、潜热通量更加准确且具有代表性。但因仪器价格昂贵、操作复杂、维护成本等限制因素, 目前该仪器只在有限的野外站点进行了部署, 无法在整个高原区域面上进行大规模的观测(杨娟等, 2006; 陈家宜等, 2006); 总体输送法(Bulk Transfer Method, TM)一般采用一个经验常数即总体输送系数描述一个地区的湍流通量与常规气象观测的风、温、湿的关系。该方法原理简单, 计算方便, 适用于业务气象站和普通野外台站只有常规观测项目的情况, 可以广泛应用于高原上。但早期研究总体输送系数的参数化方案较多, 仅用一个参数值代表整个高原, 使湍流通量结果差异较大(Cressman, 1960; 叶笃正等, 1979; 陈万隆等, 1984; Chen et al, 1985; Li et al, 2001; 李国平等, 2003)。目前的研究因缺少计算潜热通量所需要的水汽梯度信息, 一般都假定水汽廓线与温度廓线函数具有相同的积分形式, 默认CH=Cλ(李国平等, 2000), 所以关于水汽输送系数Cλ参数值的确定和变化特征还缺少具体的研究。由于高原陆面特征的复杂性和不均匀性, 现有的关于总体输送系数的研究仍然较为薄弱, 主要体现于在计算CH与Cλ时没有考虑不同下垫面特征影响下总体输送系数存在显著的空间异质性, 基于典型下垫面涡动观测所获取的“单点”总体输送系数向相同下垫面特征进行“多点”推广的研究仍是空白。在利用业务气象站数据计算湍流通量方面, 由于气象局业务台站只有一层的风、温、湿观测, 因此目前想要利用中国气象局业务台站数据直接计算潜热通量仍然是个难点。
针对上述目前面临的问题, 本研究基于中国科学院那曲高寒气候环境观测研究站那曲/BJ观测点的野外观测数据和中国气象局那曲地面气象观测站(简称那曲站)的常规气象观测数据开展总体输送系数的计算与其季节变化特征, 长时间地表湍流通量序列的年际变化趋势分析。首先, 利用野外自动观测站和行星边界层塔梯度数据定义并计算地表大气的水汽相关参数, 其次通过总体输送公式反算出基于站点的总体输送系数CH、Cλ的取值, 再次将它们应用到那曲站1980-2016年常规气象观测数据上, 计算得到一个高寒草地下垫面长时间连续的地表热通量序列, 并分析1980-2016年的地表热源变化特征。本文将涡动相关法和总体输送法相结合, 可以得到精度更高的总体输送系数, 实现由“单点”野外台站向相同下垫面特征进行“多点”业务气象台站的湍流通量计算的推广研究, 使我们可以对高原复杂而不同的地表下垫面通量做长期的、定点观测的研究, 计算得到不同下垫面上准确的热源信息。
2 数据来源和方法介绍 2.1 观测数据中国科学院那曲高寒气候环境观测研究站那曲/BJ观测点(91.90°E, 31.37°N, 海拔4509 m)位于西藏自治区那曲县西南19 km处罗玛镇娘曲村附近, 是那曲站的中心观测点。BJ观测点的观测场周围地势较为平坦开阔, 且为牧区, 下垫面植被主要是高寒草地。每年6-9月高原季风盛行时, 受较高的气温和充沛的降水影响, 植被生长茂盛, 11月至翌年5月, 气温较低, 植被枯萎, 植被高度明显低于高原季风盛行期。中国气象局那曲地面气象观测站(简称那曲站)距BJ观测点19.29 km, 其同样位于牧区, 下垫面植被类型也为高寒草地。
BJ观测点架设着自动气象塔站(AWS Tower)、行星边界层塔站(PBL Tower, 自2012年8月3日18:30建成并开始观测)、天空辐射仪、土壤温湿观测系统、涡动相关仪(3.02 m)、风廓线观测等, 其观测项目主要包括风向风速、气温、空气相对湿度、气压、降水、辐射四分量和地表通量等。本文所使用的数据为AWS、PBL获得的气象观测梯度数据和涡动相关系统(EC)的湍流观测资料, 时间步长统一调整为30 min。AWS和PBL部分项目的观测高度见表 1, 涡动系统以及辐射四分量的观测仪器和架设高度(埋深)见表 2。业务气象站(CMA)的数据主要采用了中国气象局数据网中地面气候资料日值数据, 主要包括本站气压、气温、降水量、蒸发量、相对湿度、风向风速、日照时数和0 cm地温要素。本文选用的观测资料包括气压、气温、相对湿度、风速和0 cm地温。
| 表 1 自动气象塔站、行星边界层塔站各项目的观测高度 Table 1 The height of observational instrument of AWS Tower and PBL Tower |
| 表 2 BJ观测点观测仪器说明 Table 2 Specification of observational instrument at BJ site |
涡动相关仪利用三维风速和高频水汽、气温数据的协方差来计算感热通量、潜热通量。本文中的涡动数据(EC)处理软件采用的是美国LI-COR公司推出的EddyPro软件, 它在处理涡动数据过程中, 对数据进行了严格的质量控制, 包括: (1)将因雨雪尘埃等环境因子对传感器光程干扰或是电缆电源不稳定而带来的野点去除, 以免对协方差的计算产生影响; (2)通过二次旋转法消除地面倾斜造成的误差或者湍流通量不同分量之间的交叉干扰(Kaimal et al, 1994); (3)采用Moore方法对频率损失进行修正(Morre, 1986); (4)在计算感热和潜热时采用Schotanus方法对超声虚温进行修正(Schotanus et al, 1983); (5)采用WPL方法对空气密度脉动进行修正(Webb et al, 1980)。EddyPro软件根据稳定性检验和发展湍流条件检验对通量数据进行质量评估, 将数据质量分为0, 1, 2三等:其中0级数据质量最好; 1级数据质量较好; 2级数据质量较差。为了使计算的总体输送系数的数值更加精确, 本文只采用0级通量数据进行计算。BJ观测点涡动数据感热和潜热通量的质量状况见表 3。
| 表 3 感热通量和潜热通量数据质量情况 Table 3 Quality of the sensible and latent heat flux data |
自动气象站(AWS)和行星边界层塔(PBL)的观测数据由于观测设备、观测方法、测站位置、极端天气等因素的影响, 可能导致一部分观测数据存在误差, 为了避免在后续计算中将这些误差放大, 需要对这些观测数据进行质量控制, 本文中利用了逻辑极值检验、僵值检验、时间一致性检查以及相似一致性检查四种数据质量控制方法(王超等, 2010)。对在质量控制中被剔除的常规观测数据需要选择适当的方法对空值进行插补, 本文采用了线性插补法。公式如下:
| ${D_k} = {D_{k - 1}} + \frac{{{D_{k - 1}} - {D_i}}}{{k - i - 1}}, $ | (1) |
式中: Dk、Dk-1、Di分别为缺测值, 缺测前一时刻值, 缺测值后首个非缺测值; k、i代表不同时刻。插补后数据具有了一定的完整性, 后续计算结果更加可靠, 但这种方法一般适用于数据缺测较少的情况。
2.2.3 总体输送法与总体输送系数根据总体输送理论(Stull, 1988), 近地层感热通量、潜热通量可分别表示为:
| $H = \rho {C_p}{C_H}U\left({{T_g} - T} \right), $ | (2) |
| $LE = \rho \lambda {C_\lambda }U\left({{q_g} - q} \right), $ | (3) |
式中: CH、Cλ为感热、潜热通量的总体输送系数; Cp为空气定压比热, 值为1005 J·K-1·kg-1; λ为水的汽化潜热, 值为2.5×106J·kg-1; ρ为空气密度(单位: kg·m-3); U为10 m高度处的风速(单位: m·s-1); qg、q分别为地表比湿和1.5 m高度处空气的比湿(单位: kg·kg-1); Tg、T分别为地表温度和1.5 m高度处的气温(单位: K), 本文中地表温度Tg由斯蒂芬-玻尔兹曼定律计算(盛裴轩, 2003), 公式为:
| $E_{l, 0}^ \uparrow = {\varepsilon _g}\sigma T_g^4 + \left({1 - {\varepsilon _g}} \right)E_{l, 0}^ \downarrow\;, $ | (4) |
式中: El, 0↑为地面长波辐射(单位: W·m-2); El, 0↓为大气逆辐射(单位: W·m-2); εg为地面比辐射率, 本文中取值为0.96; σ为斯蒂芬-玻尔兹曼常数, 值为5.67×10-8 W·m-2·K-4。
热量输送系数CH和水汽输送系数Cλ是表示湍流输送强度的重要参数, 也是影响地面通量计算的主要因素。本文的计算方法是倒算法, 即利用BJ观测点2011-2016年涡动观测数据(EC)得到的地表湍流通量结合自动观测站(AWS)风速、温度、湿度等气象要素的梯度观测资料, 利用总体输送公式反算得到总体输送系数, 公式如下:
| ${C_H} = \frac{H}{{\rho {C_p}U\left({{T_g} - T} \right)}}, $ | (5) |
| ${C_\lambda } = \frac{{LE}}{{\rho \lambda U\left({{q_g} - q} \right)}}. $ | (6) |
根据Monin-Obukhov相似性理论, 地表潜热通量可以表达为:
| $LE = L{E_0}F = - \rho \lambda {k^2}{z^2}\frac{{\partial U\partial q}}{{\partial z\partial z}}F, $ | (7) |
式中: LE0为未经层结订正的潜热通量; k、z、U、q和F分别为Karman常数、高度、水平风速、比湿和稳定度层结影响函数。
在常通量层假定下,
当有三个高度层(z0、z1、z2)上的风速、水汽相对湿度的观测时, 向上差分和向下差分都是为了得到高度为z1处的潜热通量, 那么可得到:
| $z_1^2\frac{{{U_2} - {U_1}}}{{{z_2} - {z_1}}}\frac{{{q_2} - {q_1}}}{{{z_2} - {z_1}}} = z_1^2\frac{{{U_1} - {U_0}{q_1} - {q_0}}}{{{z_1} - {z_0}{z_1} - {z_0}}}, $ | (8) |
由式(8)进一步得到:
| ${q_0} = {q_1} - \frac{{\left( {{U_2} - {U_1}} \right)\left( {{q_2} - {q_1}} \right){{\left( {{z_1} - {z_0}} \right)}^2}}}{{{U_1} - {U_0}\;\;\;\;\;{{\left( {{z_2} - {z_1}} \right)}^2}}}, $ | (9) |
假设z0=0, z2=2z1(本文中所用到数据的高度层为1.5 m和3 m), 当z0=0时, U0为地表风速可取为0, q0为地表比湿qg, 进而地表比湿可由下式估算:
| ${q_g} = {q_2} - \frac{{{U_2}}}{{{U_1}}}\left({{q_2} - {q_1}} \right), $ | (10) |
在土壤湿度较大或植被较茂密的情况下, 可假设地表比湿正比于饱和比湿, 即:
| ${q_g} = \gamma \cdot \frac{{\varepsilon \cdot {e_s}\left({{T_g}} \right)}}{P}, $ | (11) |
式中: ε=0.622; P为气压; es(Tg)为土壤表面温度为Tg的饱和水汽压。则可得到:
| $\gamma = \frac{{{q_g} \cdot P}}{{\varepsilon \cdot {e_s}\left({{T_g}} \right)}}, \ $ | (12) |
式中: γ为本文新定义的一个比例系数, 即地表大气相对湿度因子, 作用类似于相对湿度。
3 结果分析 3.1 总体输送系数 3.1.1 热量输送系数CH根据倒算法将2012年BJ观测点的EC感热数据和AWS观测数据进行线性回归分析得到BJ观测点热量输送系数CH的月平均值(表 4)。从表 4中可以看出, 热量输送系数CH有明显的季节变化, 具体表现为在进入夏季温度逐渐升高时它的数值开始增加, 在8月达到最大值, 随着温度逐渐降低, CH也逐渐降低, 最小值位于冬半年。
| 表 4 BJ观测点热量输送系数CH、地表大气相对湿度因子γ、水汽输送系数Cλ的多年月平均值 Table 4 The monthly average of CH, γ and Cλ at BJ site |
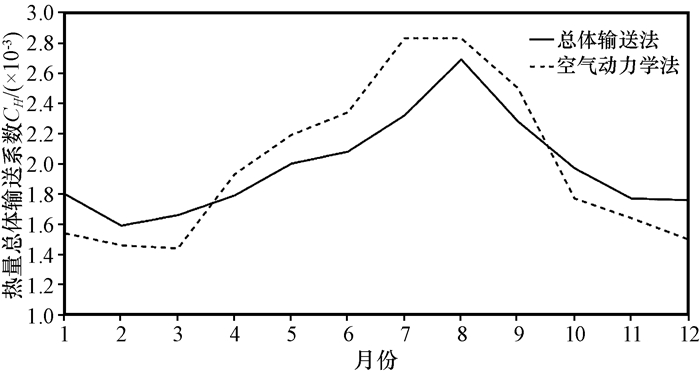
孙根厚(2016)利用依托莫宁-奥布霍夫(Monin-Obukhov)相似理论的空气动力学法并基于BJ观测点涡动数据, 计算地表粗糙程度后, 进一步计算得到2011-2012年BJ观测点的热量整体输送系数CH, 得到的数值具有代表性, 体现了BJ观测点所处的高寒草地下垫面热量的整体输送特征。将其与本文总体输送公式倒算法的计算结果进行对比(图 1)可以看出, 两种方法计算得到的感热总体输
|
图 1 两种方法计算的BJ观测点总体输送系数的对比 Fig. 1 Comparison of bulk transfer coefficients by using aerodynamic method and bulk transfer method at BJ site |
送系数都表现出显著的季节变化, 且两者具有较高的一致性, 经计算其相关系数R为0.94。在4-9月, 空气动力学法计算得到的CH在数值上略大于本文利用总体输送法计算的CH, 而在干季尤其是10月至次年3月, 空气动力学法计算得到的CH在数值上略小于本文计算的CH, 这种差异是由于计算方法不同导致的。
3.1.2 地表大气相对湿度因子γ使用业务气象站数据计算潜热通量, 获得水汽梯度是非常关键的环节。为了克服单层温湿观测在估算地表水汽时的困难, 本文定义了地表大气相对湿度因子γ, 来表征靠近地表大气的相对湿度。表 4中γ为利用2014-2016年BJ观测点PBL两层(1.5 m、3 m)的风速、水汽观测数据计算得到的1-12月多年月平均地表大气相对湿度因子的参数值, 从表 4中可以看出, 地表大气相对湿度因子的季节变化规律符合地表土壤的水分变化, 即干季时偏低, 雨季时偏高, 其最大值出现在8、9月, 约为62%, 这是由于这一时期雨水充沛, 在地表不断累积, 所以地表附近空气水汽含量随之增大; 最小值出现在2月, 约为33%, 冬季土壤冻结, 地表附近空气水汽含量较小。
3.1.3 水汽输送系数Cλ根据总体输送公式倒算法和线性回归分析得到2014-2016年BJ观测点的水汽输送系数Cλ月平均值(表 4)可以看出, 水汽输送系数Cλ在量级上与热量输送系数CH一致, 但整体略小于热量输送系数。在季节变化趋势上, 呈“双峰型”, 峰值分别出现在4月和8月。4月春季气温回暖, 冻土消融, 土壤含水量增加, Cλ的值也显著增大; 8月达全年最大值, 也是对高原雨季的直接反映。
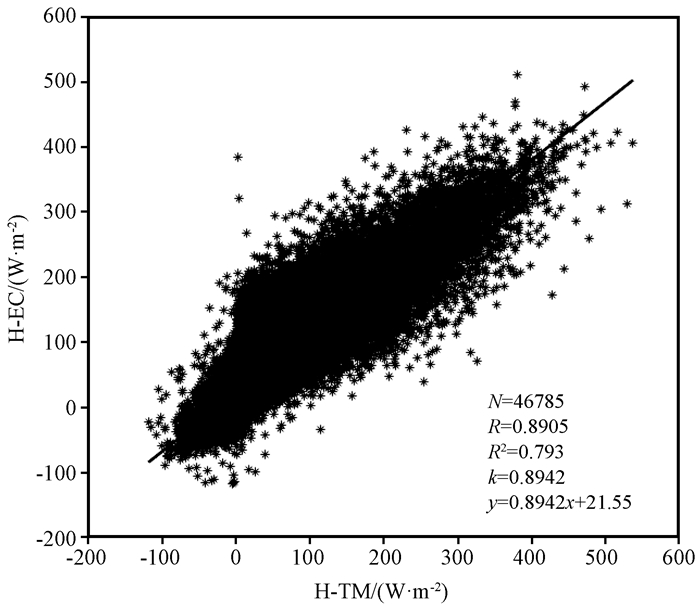
3.2 两种方法计算通量的对比分析 3.2.1 感热通量将2011-2016年涡动感热数据H_EC与总体输送法计算得到的感热数据H_TM基于每30 min的结果做一致性分析(图 2, 黑色实线是回归直线, R为相关系数, R2为决定系数, N为样本数据容量, k为拟合直线的斜率)可以看出, 将2012年计算得到的热量输送系数应用于2011-2016年, 计算的感热通量和涡动观测的感热通量具有较好的相关性, 相关系数R达到了0.8905。回归直线的拟合程度较高, 斜率k为0.8942, 与1偏差较小。
|
图 2 涡动相关法和总体输送法两种方法计算地表感热通量的相关性分析 Fig. 2 The comparison of surface sensible heat flux by using eddy covariance and bulk transfer method |
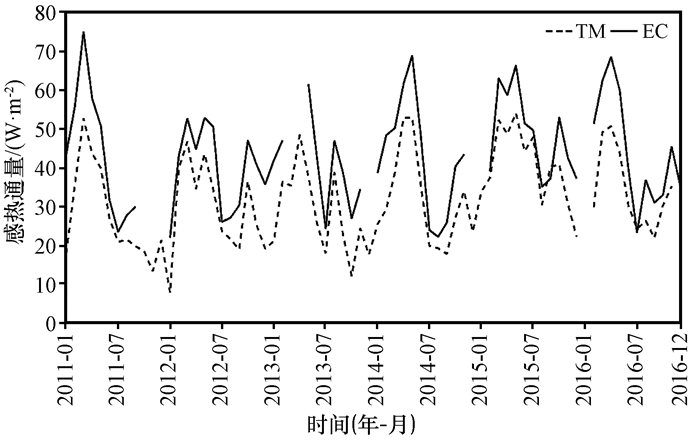
将总体输送法计算得到的感热通量与涡动观测感热通量数据进行季节变化对比(图 3), 从图 3中可以看到, 2011-2016年间, 涡动观测的感热通量月均变化范围为20~75 W·m-2, 总体输送法计算的感热通量月均变化范围10~50 W·m-2。整个时间序列, 两者的月均变化趋势较为一致, 涡动观测的感热通量月均变化最大值和最小值均大于总体输送法计算的感热通量月均变化的最大值和最小值, 二者间的差值是由于两种计算方法不同导致。
|
图 3 2011-2016年涡动相关法和总体输送法两种方法计算的感热通量的季节变化 Fig. 3 Seasonal variations of sensible heat flux by using two methods of eddy covariance and bulk transfer method from 2011 to 2016 |
所以为了在应用到业务气象站数据计算感热通量时能更加贴近涡动观测的湍流实际值, 本文对两种方法计算的感热通量做逐月的相关性分析(表 5), 表中给出了它们的线性关系和相关系数, 两种感热通量数据在各个月上具有较好的相关性, 均在0.77以上。
| 表 5 2011-2016年H_EC与H_TM的拟合关系 Table 5 The fitting function between H_EC and H_TM from 2011 to 2016 |
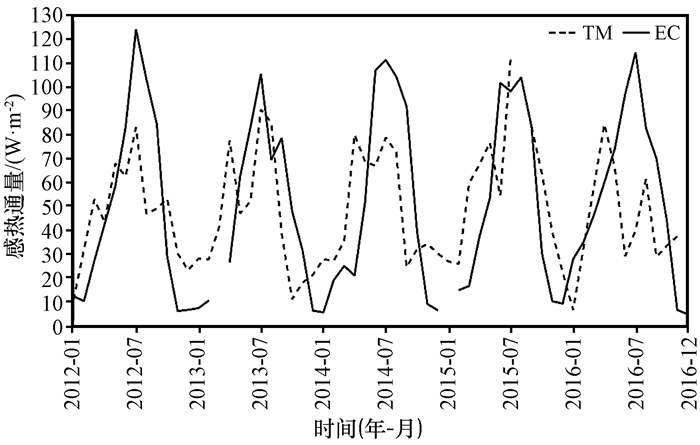
将计算得到的水汽输送系数Cλ代入总体输送公式计算潜热通量, 并将得到的结果与涡动观测潜热通量数据进行季节变化对比(图 4)可以看出, 2012-2016年, 涡动观测的潜热通量月均变化范围为0~130 W·m-2, 总体输送法计算的潜热通量月均变化范围为10~110 W·m-2。整个时间序列, 涡动观测得到的潜热通量月均值大致呈单峰值曲线, 最大值在7月, 最小值在1月; 而总体输送法计算得到的潜热通量月均值为波动型曲线, 即在4-7月, 潜热通量月均值呈波动状态, 但7月仍达到最高。
|
图 4 2012-2016年涡动相关法和总体输送法两种方法计算的潜热通量的季节变化 2012-2013年为验证方法 Fig. 4 Seasonal variations of latent heat flux by using two methods of eddy covariance and bulk transfer method. Seasonal variations of latent heat flux from 2012 to 2013 is to verify the difference between two methods |
将2012-2013年的LE_EC与LE_TM基于每30 min的结果做逐月相关性分析, 表 6为1-12月的线性关系和相关系数。表中相关系数R在4、5、10、11月时数值较低, 通过严晓强(2018)对土壤冻融过程影响地表通量变化的研究, 我们发现季节性冻土BJ站土壤完全融化阶段开始时间在4月下旬, 结束时间在10月底; 冻结过程出现在11月。那么这几个月相关系数R值较小的原因可能是由于这些月份正处于土壤冻融期节点, 在这期间地表土壤的湿度和含水量存在着显著的变化, 土壤中的水存在着相变, 使得用自动气象站观测数据估算的潜热通量LE_TM的结果不是十分理想, 与涡动观测得到的潜热通量LE_EC存在着较大的偏差。
| 表 6 2012-2013年LE_EC与LE_TM的拟合关系 Table 6 The fitting function between LE_EC and LE_TM from 2012 to 2013 |
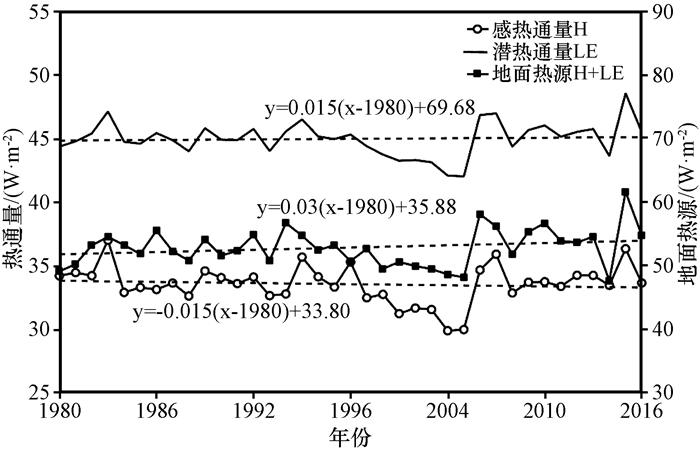
将计算得到的地表大气相对湿度因子γ、热量输送系数CH和水汽输送系数Cλ应用于与BJ观测点具有相同下垫面特征的那曲业务气象站, 以此来分析那曲地区高寒草地下垫面1980-2016年感热通量、潜热通量和地面热源的年际变化特征(图 5)。从图 5中可以看出, 1980-2016年那曲高寒草地感热通量总体呈现减弱趋势, 这与大部分研究结果显示近30年青藏高原地表感热通量呈减弱趋势较为一致(Duan et al, 2008; Yang et al, 2011; 竺夏英等, 2012); 潜热通量总体呈现上升趋势; 地面热源年际变化趋势不明显。分阶段来看, 感热通量的变化在2004年前后发生转折, 1980-1994年变化趋势不明显, 1995-2004年减弱趋势显著, 2004年后为增加趋势, 这与解晋(2018)分析高原85个站点的年平均感热通量变化特征时指出1981-2003年感热通量呈下降趋势, 在2004-2008年高原整体年平均感热通量呈逐渐增加趋势, 2008年后增加趋势减缓, 而后趋于稳定的结果相符, 以及于威(2018)得到的高原地表感热在1961-1979年呈上升趋势, 在1979-2003年呈减弱趋势, 而在2003-2014年又为上升趋势的结论较为一致。而图 5中潜热通量在1980-1993年呈微弱的波动上升趋势, 到了1994-2005年有明显下降趋势; 感热通量、潜热通量的变化也导致地面热源在1980-1994年变化趋势不明显, 而在1995-2005年有一个明显的下降趋势。
|
图 5 1980-2016年那曲站感热通量、潜热通量和地面热源的年际变化特征 Fig. 5 Variation characteristics of annual average sensible heat flux, latent heat flux and surface heat source at Naqu station from 1980 to 2016 |
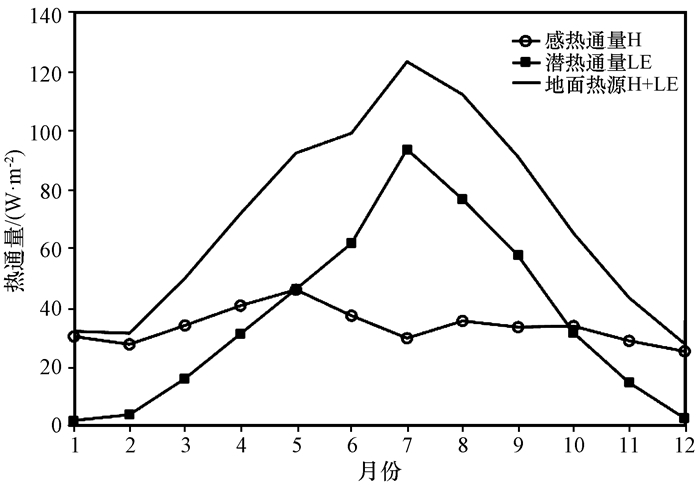
图 6为那曲站感热、潜热通量和地面热源的多年(1980-2016年)月均变化曲线。春季高原积雪逐渐消融, 地表反射率减小, 使得到达地表的太阳辐射不断增强, 地气温差增大, 感热通量逐渐增大, 并在5月达到最大值为46.11 W·m-2; 积雪融化、土壤解冻后土壤湿度增加, 土壤水分蒸发加大, 潜热通量在春季开始显著增大。到了夏季, 高原上降雨增多, 地气温差减小, 土壤湿度增大, 感热通量逐渐减小, 而潜热通量在7月时达到全年最大值为93.69 W·m-2, 这是对高原雨季的直接反映。进入秋冬季以后, 温度开始逐渐降低, 土壤慢慢冻结土壤湿度逐渐减小, 感热通量和潜热通量也随之减小, 感热通量在12月达到最小值为25.23 W·m-2, 潜热通量在1月达到最小值为1.81 W·m-2。
|
图 6 1980-2016年那曲站感热、潜热通量和地面热源多年平均的季节变化 Fig. 6 Seasonal variations of sensible heat flux, latent heat flux and surface heat source at Naqu station from 1980 to 2016 |
在年内季节变化上, 那曲站潜热通量的季节变化相较于感热通量变化更明显, 地面热源有显著的季节变化且更依赖于潜热通量的季节变化。
4 结论与讨论以估算总体输送系数和研究地面热源变化规律为核心问题, 利用野外站涡动相关系统EC和自动气象站AWS观测数据, 计算并分析了热量输送系数CH和水汽输送系数Cλ的值以及其季节变化特征, 再将其应用到业务气象站数据, 研究了那曲高寒草地下垫面地表湍流通量1980-2016年的长期变化趋势, 得到如下主要结论:
(1) 那曲/BJ观测点地表大气相对湿度因子γ的数值在33%~62%, 9月最大, 2月最小; 感热和潜热总体输送系数都存在着明显的季节变化, 热量输送系数CH月平均值范围在1.6×10-3~2.7×10-3, 水汽输送系数Cλ略小, 月平均值范围在1.0×10-3~2.0×10-3。
(2) 总体输送法计算的感热通量与涡动观测得到的感热通量在各个月上具有较好的相关性, 均在0.77以上; 而两种方法计算得到的潜热通量在夏季和冬季的相关性较好, 在春季4、5月和秋季10、11月较差, 只有0.4左右。
(3) 1980-2016年那曲业务气象站代表的高寒草地下垫面的湍流通量在年际变化上, 感热通量总体呈现减弱趋势, 而潜热通量呈现增强趋势, 导致地面热源变化趋势不明显; 分阶段来看, 感热通量的变化在2004年前后发生转折, 转折点前后的趋势为先减弱后增加, 潜热通量在1994-2005年下降趋势明显, 这也导致地面热源在1995-2005年有一个明显的减少。
(4) 在年内季节变化上, 地面热源有显著的季节变化, 潜热通量的季节变化相较于感热通量变化更明显。感热通量在5月达到全年最大值, 在12月达到最小值; 潜热通量在7月为全年最大值, 在1月为最小值。
本文的研究为建立高原不同地表下垫面长时间通量序列提供一套较为合理的参数和方法, 有助于我们更加深入地了解高原地气相互作用过程。但是在研究过程中, 目前只计算了一个野外观测点(那曲/BJ观测点)的地表大气相对湿度因子γ及热量和水汽输送系数CH与Cλ, 并将计算结果应用到了那曲高寒草地下垫面, 后续工作会将研究结果扩展到其他站点, 以适应青藏高原多种下垫面的应用。
Chen L, Reiter E R, Feng Z. 1985. The atmospheric heat source over the Tibetan Plateau:May-August 1979[J]. Monthly Weather Review, 113: 1771–1790.
DOI:10.1175/1520-0493(1985)113<1771:TAHSOT>2.0.CO;2 |
|
Cressman G P. 1960. Improved terrain effects in barotropic forecasts[J]. Monthly Weather Review, 88: 327–342.
DOI:10.1175/1520-0493(1960)088<0327:ITEIBF>2.0.CO;2 |
|
Duan A, Wu G. 2008. Weakening trend in the atmospheric heat source over the Tibetan Plateau during recent decades.Part Ⅰ:Observations[J]. Journal of Climate, 21(13): 3149–3164.
DOI:10.1175/2007JCLI1912.1 |
|
Dyer A J. 1974. A review of flux-profile relationships[J]. Boundary-Layer Meteorology, 7(3): 363–372.
DOI:10.1007/BF00240838 |
|
Kaimal J C, Finnigan J J. 1994. Atmospheric boundary layer flows:their structure and measurement[M]. Oxford: Oxford university press.
|
|
Li G, Duan T, Gong Y, et al. 2001. Estimates of the bulk transfer coefficients and surface fluxes over the Tibetan Plateau using AWS data[J]. Journal of the Meteorological Society of Japan, 79(2): 625–635.
DOI:10.2151/jmsj.79.625 |
|
Moore C J. 1986. Frequency response corrections for eddy correlation system[J]. Boundary-Layer Meteorology, 37: 17–35.
DOI:10.1007/BF00122754 |
|
Schotanus P, Nieuwstadt F T M, Debruin H A R. 1983. Temperature measurement with a sonic anemometer and its application to heat and moisture fluctuations[J]. Boundary-Layer Meteorology, 26: 81–93.
DOI:10.1007/BF00164332 |
|
Stull R B, 1988.An introduction to boundary layer meteorology[M].Springer Science & Business Media.
|
|
Webb E K, Pearman G I, Leuning R. 1980. Correction of the flux measurements for density effects due to heat and water vapour transfer[J]. Quarterly Journal of Royal Meteorological Society, 106: 85–100.
DOI:10.1002/(ISSN)1477-870X |
|
Yaglom A M. 1977. Comments on wind and temperature flux-profile relationships[J]. Boundary-Layer Meteorology, 11(1): 89–102.
DOI:10.1007/BF00221826 |
|
Yanai M. 1992. Seasonal Heating of the Tibetan Plateau and Its Effects on the Evolution of the Asian Summer Monsoon[J]. Journal of the Meteorological Society of Japan, 79(1): 419–434.
|
|
Yang K, Guo X F, Wu B Y. 2011. Recent trends in surface sensible heat flux on the Tibetan Plateau[J]. Science in China Series (Earth Sciences), 54(1): 19–28.
DOI:10.1007/s11430-010-4036-6 |
|
陈家宜, 范邵华, 赵传峰, 等. 2006. 涡旋相关法测定湍流通量偏低的研究[J]. 大气科学, 30(3): 423–432.
|
|
陈万隆, 翁笃鸣, 1984.关于青藏高原感热和潜热旬总量计算方法的初步研究[C]//青藏高原气象科学实验论文集(二).北京: 科学出版社: 35-45.
|
|
陈忠明, 闵文彬, 刘富明. 2003. 青藏高原地表热源异常与四川盆地夏季降水的关联[J]. 气象, 29(5): 9–12.
|
|
李栋梁, 陈丽萍. 1990. 青藏高原地面加热场强度与东亚环流及西北初夏旱的关系[J]. 应用气象学报, 1(4): 383–391.
|
|
李国平, 段廷扬, 巩远发. 2000. 青藏高原西部地区的总体输送系数和地面通量[J]. 科学通报, 45(8): 865–869.
|
|
李国平, 段廷扬, 吴贵芬. 2003. 青藏高原西部的地面热源强度及地面热量平衡[J]. 地理科学, 23(1): 13–18.
|
|
刘树华, 黄子琛, 刘立超, 等. 1995. 空气动力学方法在湍流通量计算中的误差分析[J]. 气象, 21(3): 3–6.
|
|
梁玲, 李跃清, 胡豪然, 等. 2013. 青藏高原夏季感热异常与川渝地区降水关系的数值模拟[J]. 高原气象, 32(6): 1538–1545.
DOI:10.7522/j.issn.1000-0534.2013.00028 |
|
孙根厚, 2016.藏北地区高寒草地地表通量的尺度扩展分析[D].兰州: 中国科学院寒区旱区环境与工程研究所, 46-48.
|
|
盛裴轩. 2003. 大气物理学[M]. 北京: 北京大学出版社.
|
|
王超, 韦志刚, 李振朝. 2010. 敦煌戈壁气象塔站资料的质量控制[J]. 干旱气象, 28(2): 121–127.
|
|
解晋, 余晔, 刘川, 等. 2018. 青藏高原地表感热通量变化特征及其对气候变化的响应[J]. 高原气象, 37(1): 28–42.
DOI:10.7522/j.issn.1000-0534.2017.00019 |
|
叶笃正, 高由禧. 1979. 青藏高原气象学[M]. 北京: 科学出版社.
|
|
杨娟, 周广胜, 王云龙, 等. 2006. 基于变分方法的内蒙古典型草原水热通量估算[J]. 应用生态学报, 17(11): 2046–2051.
|
|
于威, 刘屹岷, 杨修群, 等. 2018. 青藏高原不同海拔地表感热的年际和年代际变化特征及其成因分析[J]. 高原气象, 37(5): 1161–1176.
DOI:10.7522/j.issn.1000-0534.2018.00027 |
|
严晓强, 胡泽勇, 孙根厚, 等. 2018. 那曲高寒草地上四种地表通量计算方法的对比[J]. 高原气象, 37(2): 358–370.
DOI:10.7522/j.issn.1000-0534.2017.00067 |
|
严晓强, 2018.藏北高寒草地下垫面地-气能量交换特征及气候因子分析[D].兰州: 中国科学院西北生态环境资源研究院, 15-17.
|
|
周俊前, 刘新, 李伟平, 等. 2016. 青藏高原春季地表感热异常对西北地区东部降水变化的影响[J]. 高原气象, 35(4): 845–853.
DOI:10.7522/j.issn.1000-0534.2015.00053 |
|
周秀骥, 赵平, 陈军明, 等. 2009. 青藏高原热力作用对北半球气候影响的研究[J]. 中国科学(地球科学), 39(11): 1473–1486.
|
|
竺夏英, 刘屹岷, 吴国雄. 2012. 夏季青藏高原多种地表感热通量资料的评估[J]. 中国科学(地球科学), 42(7): 1104–1112.
|
|
张艳, 钱永甫. 2002. 青藏高原地面热源对亚洲季风爆发的热力影响[J]. 南京气象学院学报, 25(3): 298–306.
|
2. Center for Excellence in Tibetan Plateau Earth Science, Chinese Academy of Science, Beijing 100101, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China;
4. School of Atmospheric Sciences, Sun Yat-Sen University, Guangzhou 510275, Guangdong, China;
5. Institute of Tibetan Plateau, Chinese Academy of Sciences, Beijing 100101, China;
6. Chengdu Meteorological Administration, Chengdu 610071, Sichuan, China
 2019, Vol. 38
2019, Vol. 38
