1 引言
2 数据来源和方法介绍
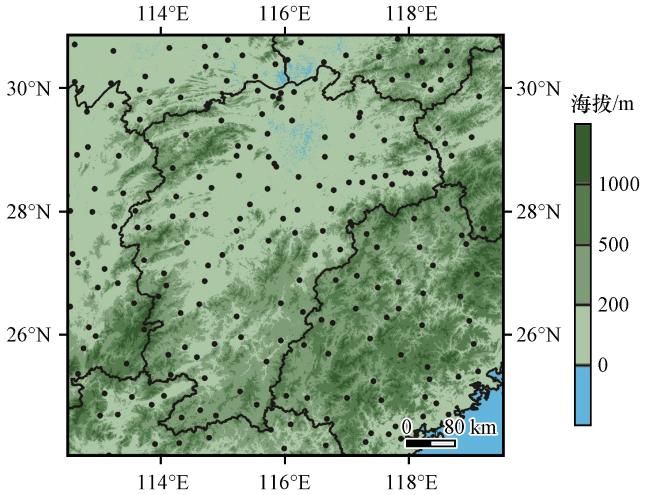
2.1 数据来源和研究区域
2.2 研究方法
2.2.1 模型数据预处理
表1 各预报时效训练集、 验证集和测试集的样本数量Table 1 Number of samples in the training, validation, and test datasets for each forecast time |
| 预报 时效 /h | 训练集样本/个 2020/01/01 - 2021/6/31 | 验证集样本/个 2021/07/01 - 2021/12/31 | 测试集样本/个 2022/01/01 - 2022/03/31 |
|---|---|---|---|
| 3 | 13637 | 2084 | 2087 |
| 4 | 13627 | 2084 | 2085 |
| 5 | 13615 | 2084 | 2086 |
| 6 | 13605 | 2084 | 2083 |
| 7 | 13609 | 2084 | 2083 |
| 8 | 13606 | 2084 | 2082 |
| 9 | 13602 | 2084 | 2082 |
| 10 | 13597 | 2084 | 2082 |
| 11 | 13586 | 2084 | 2082 |
| 12 | 13582 | 2084 | 2082 |
| 13 | 13581 | 2084 | 2082 |
| 14 | 13570 | 2083 | 2082 |
| 15 | 13567 | 2083 | 2082 |
| 16 | 13564 | 2082 | 2082 |
| 17 | 13561 | 2082 | 2082 |
| 18 | 13556 | 2081 | 2080 |
| 19 | 13555 | 2081 | 2081 |
| 20 | 13550 | 2080 | 2080 |
| 21 | 13545 | 2080 | 2080 |
| 22 | 13540 | 2080 | 2080 |
| 23 | 13531 | 2080 | 2081 |
| 24 | 13523 | 2080 | 2081 |
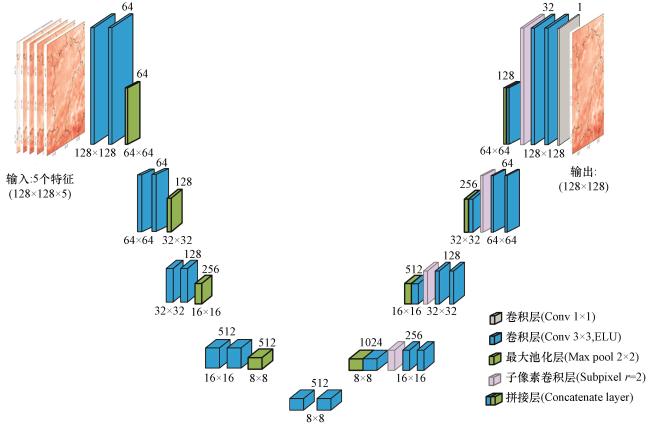
2.2.2 模型架构
2.2.3 模型参数
2.2.4 检验方法
3 结果检验分析
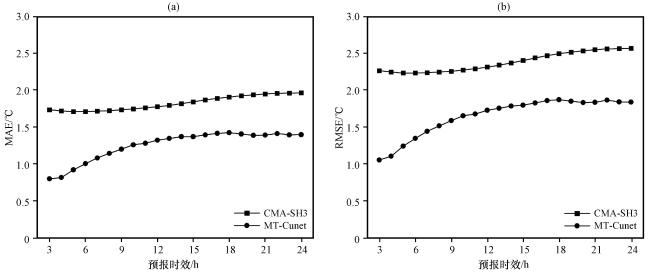
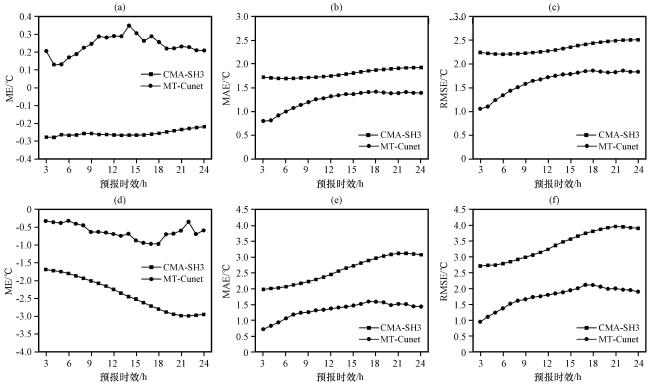
3.1 全年预报结果检验
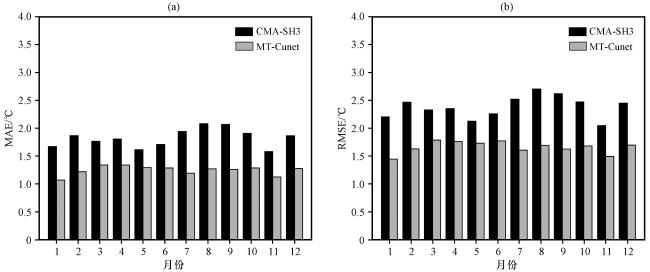
3.2 预报误差月变化特征
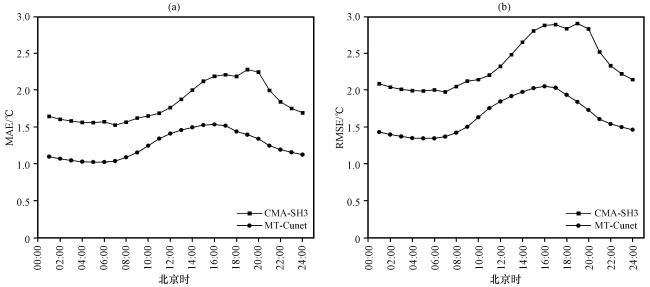
3.3 预报误差日变化特征
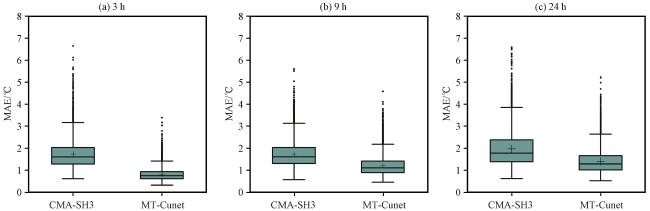
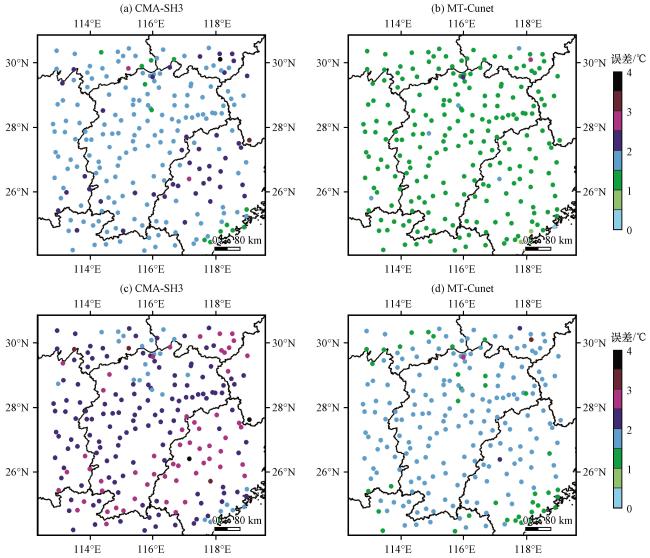
3.4 预报误差空间分布特征
表2 不同海拔分类区间的MAE和RMSETable 2 The MEA and RMSE for different altitude classification intervals |
| 模式 | 评估 指标 | <200 m (Ⅰ) | 200~500 m (Ⅱ) | 500~1000 m (Ⅲ) | >1000 m (Ⅳ) |
|---|---|---|---|---|---|
| CMA- SH3 | MAE/℃ | 1.7 | 2.0 | 1.8 | 3.0 |
| RMSE/℃ | 2.3 | 2.6 | 2.3 | 3.5 | |
| MT- Cunet | MAE/℃ | 1.2 | 1.3 | 1.3 | 2.5 |
| RMSE/℃ | 1.6 | 1.7 | 1.7 | 3.1 |
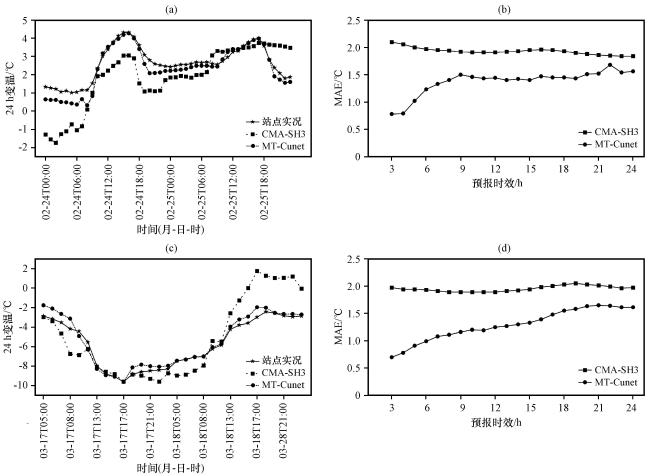
3.5 转折性天气过程检验
图9 2022年2月24 -25日增暖过程(上)和3月17 -18日寒潮过程(下)CMA-SH3和MT-Cunet的24 h变温(a, c), 以及T2m预报的MAE(b, d)对比Fig.9 Comparison of 24 h temperature changes (a, c) of CMA-SH3 and MT-Cunet, and the MAE (b, d) of T2m forecasts during the warming process from 24 to 25 February (up) and cold wave process from 17 to 18 March (down) 2022 |