Plateau Meteorology

Plateau Meteorology >

2024 , Vol. 43 >Issue 2: 520 - 528

DOI: https://doi.org/10.7522/j.issn.1000-0534.2023.00068

An Advection Scheme using Paired Explicit Runge-Kutta Time Integration for Atmospheric Modeling

  • Zhaoyang SUN , 1 ,
  • Chungang CHEN , 1 ,
  • Xingliang LI 2 ,
  • Xueshun SHEN 2
Expand
  • 1. Department of Mechanics，Xi’an Jiaotong University，Xi’an 710049，Shaanxi，China
  • 2. Center for Earth System Modelling and Predication，China Meteorological Administration，Beijing 100081，China

Received date: 2023-02-14

  Revised date: 2023-08-23

  Online published: 2024-03-26

Copyright

© Editorial Department of Plateau Meteorology （CC BY-NC-ND）
Fold

Abstract

In this paper， a new numerical scheme was proposed to solve the advection equation in a multi-moment nonhydrostatic dynamical core.To guarantee the shape-preserving property， the limiting operations are devised for a hybrid discretization framework adopted by the multi-moment dynamical core， consisting of the multi-moment finite-volume and the conservative finite-difference schemes for the horizontal and vertical discretizations respectively.In the horizontal direction， a nonoscillaory scheme is accomplished by adjusting the slope of the multi-moment reconstruction polynomial at the cell center with the application of a WENO （weighted essentially non-oscillatory） algorithm.The resulting multi-moment scheme can achieve the fourth-order accuracy in the convergence test.In the vertical direction， a TVD （total variation diminishing） slope limiter is applied in the finite-difference discretization to remove the non-physical oscillations around the discontinuities.To accomplish the time marching in the proposed advection model， a second-order paired explicit Runge-Kutta scheme is adopted， which is expected to be an efficient and practical method for the advection solvers in the atmospheric models with very high spatial resolutions.The explicit time marching， without the dimension splitting， is useful to avoid the divergence errors in the advection transport calculations.Two Runge-Kutta schemes， requiring different times of conducting the spatial discretization within a time step， are combined， and used for the time marching in the different directions.The finite-difference discretization is called for six times within a time step in order to increase the maximum available CFL （Courant-Friedrichs-Lewy） number in the vertical direction， while the horizontal multi-moment spatial discretization is conducted for two times as the regular second-order schemes.As a result， the difference between the maximum time steps determined by the horizontal and vertical discretizations， due to the very large aspect ratio of the computational cells in atmospheric modeling， can be diminished.The non-negativity property of the proposed advection scheme is assured by devising a new flux-correction algorithm.It improves the existing positivity-preserving algorithm through further considering the mass flowing into the computational cell in an iterative procedure during the flux-correction operations.The proposed flux-correction algorithm can approach the necessary and sufficient condition for assuring the non-negative solutions and is more accurate for the advection calculations with CFL numbers larger than one.The widely used two-dimensional benchmark tests were checked in this study and the numerical results verified the performance the proposed advection scheme， which has the practical potential to build an accurate and efficient advection equation solver for the scalable high-resolution nonhydrostatic atmospheric models.

Key words： advection equation; paired explicit Runge-Kutta scheme; slope limiter; non-negative scheme; multi-moment method

Cite this article

Zhaoyang SUN , Chungang CHEN , Xingliang LI , Xueshun SHEN . An Advection Scheme using Paired Explicit Runge-Kutta Time Integration for Atmospheric Modeling[J]. Plateau Meteorology, 2024 , 43(2) : 520 -528 . DOI: 10.7522/j.issn.1000-0534.2023.00068

1 引言

应对大气科学研究和数值预报应用对精细化仿真的迫切需求， 高分辨率非静力模式的研发已成为大气模式发展领域的研究热点。高分辨率大气模式需要海量计算资源， 其实际应用水平高度依赖于超级计算机的发展和高效利用。因此， 提高数值算法的并行计算可扩展性是当前高分辨率模式发展的核心问题之一。在时间积分方面， 水平显式-垂直隐式（horizontally explicit and vertically implicit， HEVI）方法是构建高可扩展数值模式的一条有效途径。Weller et al （2013）和Gardner et al （2018）开展了HEVI方法在大气模型方程及高精度动力框架中的应用研究， 比较分析了不同的HEVI实施方案。Gardner et al （2018）还针对超高分辨率数值模拟设计了显式计算垂直平流过程的时间积分策略。在模式中显式计算垂直平流过程， 可为发展高保真平流计算方案提供便利。对于高可扩展欧拉类模式， 我们可以使用与动力过程相同的算法框架计算平流输送问题， 能在垂直方向直接应用基于欧拉框架发展的各类保形和正定限制策略。显式平流计算可避免采用方向分裂算法时导致的散度计算误差和引入的复杂修正算法（Blossey and Durran， 2008）， 以及非线性限制器在隐式时间积分中可能遇到的适用性和收敛性难题（Arbogas et al， 2020）。
Vermeire （2019）提出了用于求解方向依赖刚性问题的二阶成对显式龙格-库塔（paired explicit Runge-Kutta， P-ERK）时间积分方法。该方法通过组合两种精度相同、 但内循环中空间离散调用次数不同的显式龙格-库塔积分格式， 来缓解某方向的刚性项对数值模型积分步长的限制。成对龙格-库塔时间积分方法可用于HEVI时间积分的显式部分， 对具有不同刚性特征的项采用不同的时间推进策略， 从而进一步提高模式计算效率。在显式大气平流计算方案中应用成对龙格-库塔时间积分方法， 可在垂直方向增加龙格-库塔内循环中空间离散调用次数， 增大垂直方向的许用CFL数， 缓解垂直小网格距对平流计算时间步长的限制； 同时， 在水平方向减少复杂度更高的水平空间离散实施次数， 保证平流方程求解器的整体计算效率。
我们采用多矩-有限差分混合算法发展了基于立方球网格的非静力全球大气动力框架（Chen et al， 2023）。该框架在水平方向使用基于局地重构的四阶多矩有限体积算法完成空间离散， 保证模式计算精度和大规模并行计算可扩展性； 在垂直方向使用二至三阶的守恒有限差分算法， 便于完成动力框架与物理过程软件包的耦合。在本研究中， 我们将通过在多矩有限体积和有限差分算法中添加相应的保形、 正定限制器， 进一步发展具有高保真特性的大气平流方程算法。平流求解器使用显式成对龙格-库塔方法完成时间推进， 通过合理设计水平、 垂直方向的内循环空间离散调用次数， 对计算效率进行优化。
本文将在第二节中介绍所提出的平流方程时空离散格式； 在第三节中通过常用标准算例检验所提出算法的仿真性能； 最后， 在第四节中简要小结本研究并展望未来工作。

2 高保真平流方程算法

在二维笛卡尔（ x - z）网格上， 求解平流方程
∂ q ∂ t + ∂ e ∂ x + ∂ f ∂ z = 0
式中： q为输送量； e = u q和 f = w q是 x和 z方向的通量函数， u , w为二维速度矢量。
平流算法采用多矩非静力大气动力框架（Chen et al， 2023）的空间离散策略， 在水平方向使用多矩有限体积方法， 在垂直方向使用守恒的有限差分方法完成空间离散。
在二维笛卡尔网格计算单元 C i j中的局地自由度定义如图1所示。在每个计算单元中定义三个局地自由度， 均为输送量 q x , z , t的点值， 即： q i m , j t = q ( x i m , z j , t ) m = 1 ~ 3。局地自由度在水平（ x）方向等距分布， 分别位于单元左、 右边界（ x = x i ± 1 2）和单元中点（ x = x i）处； 在垂直（ z）方向， 自由度均定义在相应线段的中点位置（ z = z j）。
图1 局地自由度（未知数）定义

Fig.1 Definition of local degrees of freedom （unknowns）

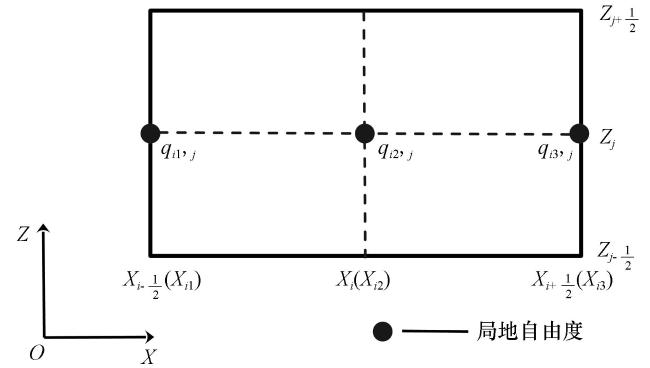
2.1　空间离散格式

求解平流方程（1）的关键问题是近似计算通量函数 e和 f的空间偏导数。
在 x方向， 采用多矩有限体积方法， 不同位置的通量函数导数 ∂ e ∂ x用以下公式计算
∂ e ∂ x i 1 = 1 2 ∂ E i - 1 x ∂ x i 1 + ∂ E i x ∂ x i 1 + u 2 ∂ Q i - 1 x ∂ x i 1 - ∂ Q i x ∂ x i 1 ∂ e ∂ x i 3 = 1 2 ∂ E i x ∂ x i 3 + ∂ E i + 1 x ∂ x i 3 + u 2 ∂ Q i x ∂ x i 3 - ∂ Q i + 1 x ∂ x i 3 ∂ e ∂ x i 2 = 3 2 e i 3 - e i 1 ∆ x - 1 4 ∂ e ∂ x i 1 + ∂ e ∂ x i 3
式中： E x x和 Q x x分别为通量函数 e和输送量 q在水平方向的空间重构函数。简单起见， 我们在这里忽略了 z方向的下标 j。
在单元水平边界处， 我们通过求解导数黎曼问题确定通量导数； 在单元中心， 通量导数的计算公式用单元积分平均值作为约束条件导出。考虑单元积分平均值 q ¯ i = 1 6 q i 1 + 4 q i 2 + q i 3， 多矩算法能在数值离散过程中保证严格质量守恒（Ii et al， 2009）。
在 z方向， 使用守恒的有限差分方法， 通量函数导数 ∂ f ∂ z近似为（类似的， 忽略水平方向下标）
∂ f ∂ z j = 1 ∆ z h j + 1 2 - h j - 1 2
式中： 辅助函数 h与通量函数 f满足 f z = ∫ z - ∆ z 2 z + ∆ z 2 h ξ d ξ。在单元垂直边界处， 辅助函数的值通过求解黎曼问题得到
h j + 1 2 = 1 2 H j z j + 1 2 + H j + 1 z j + 1 2 + w 2 Q j z z j + 1 2 - Q j + 1 z z j + 1 2
式中： H和 Q z为辅助函数 h和输送量 q在垂直方向的空间重构函数。
关于空间离散过程的详细描述可以参考Chen et al （2023）。篇幅原因， 这里不再赘述。

2.2　保形限制器

为构造保形的平流算法， 我们分别在水平和垂直方向空间重构中加入斜率限制器， 以消除输送量数值解在间断或大梯度分布区域附近产生的非物理振荡。
在水平方向， 我们利用三个局地自由度点值 q i 1， q i 2， q i 3和中点斜率 d i x作为空间重构约束条件， 得到三次拉格朗日插值函数
Q i x x = c i 0 + c i 1 ( x - x i ) + c i 2 ( x - x i ) 2 + c i 3 ( x - x i ) 3
根据前期研究， 通过改变中点斜率 d i x的计算模板可以调节算法的数值特性， 发展无振荡的多矩格式（Xiao and Yabe， 2001）。Sun et al （2015）和Tang et al （2018）中采用基于WENO思想的中点斜率计算公式， 提出了具有四阶精度的高保真算法。本研究采用此格式完成水平空间离散， 具体重构过程可参见Tang et al （2018）。
在垂直方向， 我们使用TVD限制器（Collela and Woodward， 1984）计算线性插值函数的斜率， 即：
Q j z z = q j + d j z ( z - z j )
式中
d j Z = 1 Δ z m i n m o d [ β ( q j - q j - 1 ) , β ( q j + 1 - q j ) , 0.5 ( q j + 1 - q j - 1 ) ]
minmod算子为
m i n m o d a , b , c = s g n a m i n a , b , c , a b c > 0 0 , 其他
本研究中取 β = 1.1。
通量函数 e和辅助函数 h的空间重构函数可使用相同的方法进行构造。

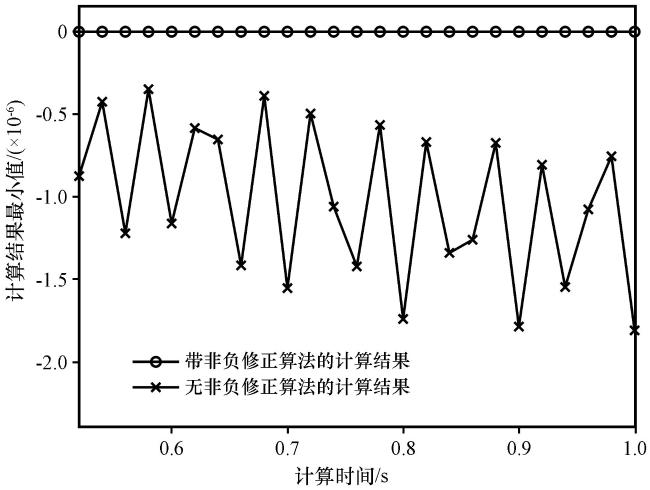
2.3　正定通量修正

考虑离散单元 C i j内的输送量积分平均值 q ¯ i j， 其在 Δ t时长内的变化可写为
q ¯ i j n + 1= q ¯ i j n + Δ t M i j i n - M i j o u t
式中： q ¯ i j n， q ¯ i j n + 1为 t n和 t n + 1时刻的积分平均值； M i n和 M o u t是 Δ t时长内流入、 流出单元的平均质量流量， 可由单元边界通量确定。这里， q ¯ i j n， M i n和 M o u t均为非负值。
Smolarkiewicz （1989）通过修正单元边界通量， 限制流出单元的质量流量 M i j o u t， 保证 M i j o u t ≤ q ¯ i j n ∆ t， 建立了保持正定的平流格式。考虑算法实施的简便性， 在修正单元边界通量时， 该算法没有考虑流入单元的质量流量 M i j i n， 因此该算法实际建立了保证平流格式正定的充分而非必要条件。
Li et al （2020）将修改后的通量修正算法应用到多矩有限体积方法， 构建了能够保持正定的多矩平流计算方案。然而， 数值试验表明： 当CFL数大于1时， 该通量修正算法无法直接应用于本研究所发展的平流计算方案。为此， 本研究中设计了通量迭代修正方法， 以解决正定修正算法在大CFL数计算中的适用性问题。新的迭代修正算法实施过程如下所述。
首先， 令 M i j i n   ( 0 )=0， 修正单元边界通量， 使得 M i j o u t   ( 1 ) ≤ q ¯ i j n ∆ t， 并计算 M i j i n   ( 1 )。可知此时有
q ¯ i j ( 1 ) = q ¯ i j n + Δ t M i j i n ( 1 ) - M i j o u t ( 1 ) ≥ Δ t M i j i n ( 1 ) ≥ 0
当CFL数大于1时， 进入以下迭代修正过程（预先设定迭代次数为 p m a x）。
（1） 再次修正单元边界通量， 使得 M i j o u t   ( 2 ) ≤ q ¯ i j n ∆ t+ M i j i n   ( 1 )。
（2） 计算 M i j i n   ( 2 )。由于在任意单元边界上第二步修正所得流出通量不小于第一次修正所得值， 可知 M i j i n   ( 2 ) ≥ M i j i n   ( 1 )， 所以
q ¯ i j ( 2 ) = q ¯ i j n + Δ t M i j i n ( 2 ) - M i j o u t ( 2 ) ≥ Δ t M i j i n ( 2 ) - M i j i n ( 1 ) ≥ 0
（3）检查迭代次数。未达到迭代次数上限则令 M i j i n   ( 1 ) = M i j i n   ( 2 )， 并再次执行步骤（1）和（2）； 达到迭代次数上限后取
q ¯ i j n + 1 = q ¯ i j ( 2 )
通过引入迭代过程， 本文提出的通量修正算法可以逼近保证数值解非负的充分必要条件。

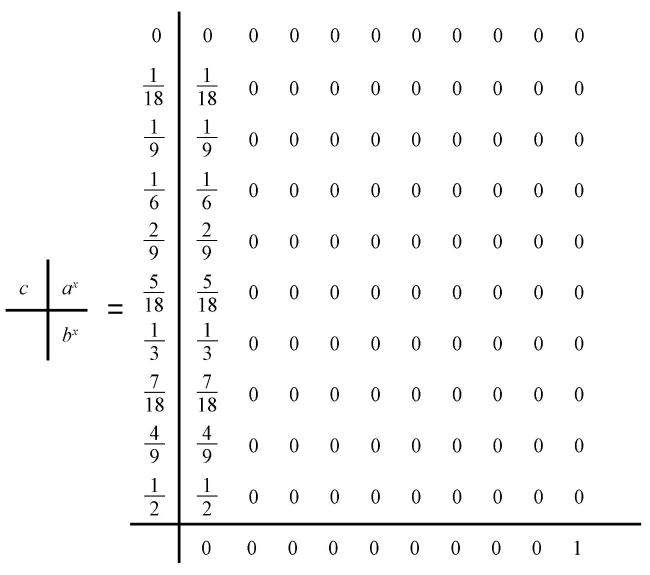
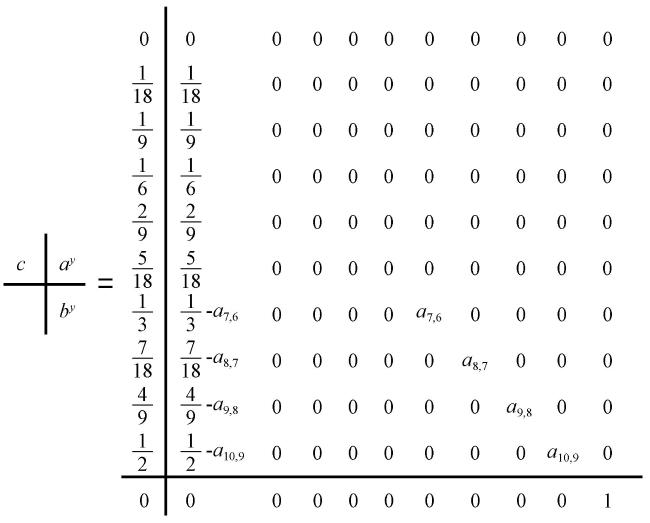
2.4　时间推进方法

完成空间离散后， 采用内循环步数为10的成对显式龙格-库塔时间积分方法（Vermeire， 2019）求解以下常微分方程
d q d t = L x q + L z q
式中： L x和 L z分别代表 x和 z方向的空间离散； L z为刚性项。
已知 t n时刻的数值解 q n， 下一时刻的数值解由下式计算
q n + 1 = q n + Δ t ∑ p = 0 9 ( b p x k p x + b p z k p z )
式中： k p x = L x q p； k p z = L z q p； q p = q n + Δ t ∑ s = 0 p - 1 ( a p s x k s x + a p s z k s z )； 系数 a x， a z， b x和 b z如图2、 3中所示； 参数 a 7,6， a 8,7， a 9,8和 a 10,9见Vermeire （2019）。
图2 x方向龙格-库塔时间积分布彻表

Fig.2 Butcher tableau of Runge-Kutta time integration in x-direction

图3 z方向龙格-库塔时间积分布彻表

Fig.3 Butcher tableau of Runge-Kutta time integration in y-direction

使用成对龙格-库塔时间积分， 每时间步内在 x方向调用2次多矩有限体积空间离散， 在 z方向调用6次有限差分离散。通过在 z方向实施更多次的空间离散计算， 可提高 z方向的可用CFL数， 使得由不同方向稳定性条件决定的时间步长尽可能接近。
我们在龙格-库塔时间积分过程的第0及9子步实施上述正定修正。在第0步， 通过修正 t n时刻的数值解 q n， 使得由 q n + Δ t k 0 x + k 0 z计算得到的数值解中间值的积分平均值为非负。在第9步， 通过修正 q 9保证 t n + 1时刻的数值解 q n + 1的积分平均值为非负。

3 数值试验与结果

本节中将采用二维标准算例对提出的平流算法进行验证， 通过定量化考察以下基于单元积分平均值的归一化误差（Williamson et al， 1992）
l 1 = ∫ Ω q ¯ - q ¯ e d Ω ∫ Ω q ¯ e d Ω , l 2 = ∫ Ω q ¯ - q ¯ e 2 d Ω ∫ Ω q ¯ e 2 d Ω 和
l ∞ = m a x q ¯ - q ¯ e m a x q ¯ e，
来分析和比较数值试验结果， 式中 q ¯和 q ¯ e分别为数值解和解析解， Ω为计算域。

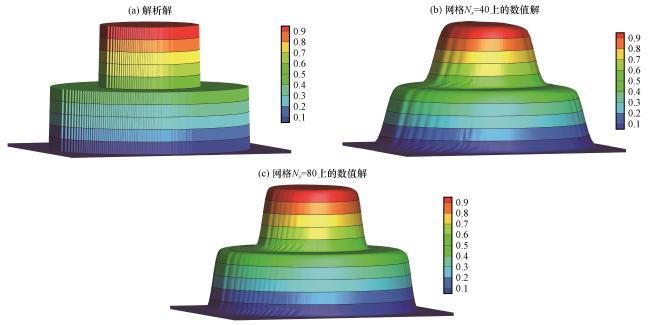
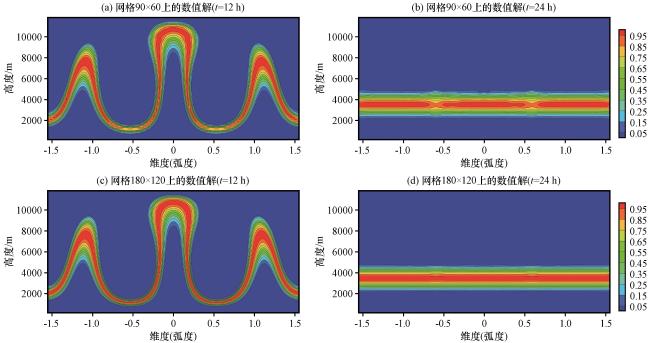
3.1　平面二维试验

在给定的区域内求解二维常风速平流方程。计算域为 - 1,1 × - 1,1， 采用周期边界条件。速度场为 u = 2 , w = 2， 计算持续一个周期， 即截止时刻为 t = 1。试验中， x和 z方向的计算单元数量满足 N z = 12.5 N x， 通过在垂直方向采用更多的计算网格提高垂直方向CFL数， 以模拟大气模式的网格特点。

3.1.1　收敛性试验

计算光滑的正弦波平流， 输送量的初始条件为
q x , z , 0 = 1 + s i n   π x + z
我们在一系列不断加密的网格（ N x=20， 40， 80）上计算了正弦波平流， 数值结果的归一化误差及收敛性情况见表1。
表1 平流算法的收敛性测试

Table 1 Convergence test of advection schemes

N x N t l 1     e r r o r（ × 10 - 4） order l 2     e r r o r（ × 10 - 4） order l ∞     e r r o r（ × 10 - 4） order
noLIM 20 200 32.16 - 29.16 - 25.25 -
40 800 2.009 4.001 1.822 4.000 1.578 4.000
80 3200 0.1256 4.000 0.1139 4.000 0.0986 4.000
hWENO 20 200 32.16 - 29.16 - 25.27 -
40 800 2.009 4.001 1.822 4.000 1.578 4.001
80 3200 0.1256 4.000 0.1139 4.000 0.0986 4.000
vTVD 20 200 34.02 - 31.06 - 26.92 -
40 800 2.555 3.735 2.309 3.750 1.995 3.754
80 3200 0.2717 3.233 0.2396 3.269 0.2020 3.304
FCT 20 200 33.97 - 31.04 - 26.88 -
40 800 2.554 3.733 2.308 3.749 1.995 3.752
80 3200 0.2714 3.234 0.2394 3.269 0.2020 3.304
本文中共对四种不同配置的平流算法进行了检验， 分别为： 不使用任何限制器的平流算法（noLIM scheme）、 包含水平WENO限制器的平流算法（hWENO scheme）、 包含垂直TVD限制器的平流算法（vTVD scheme）和包含正定修正的平流算法（FCT scheme）。在实际大气运动中， 水平方向的空间离散是计算误差的主要来源。本试验中除减小垂直网格距凸显水平空间离散误差外， 还加快了时间积分步长的加密速度， 以去除二阶时间积分格式离散误差对算法收敛速度的限制。从数值结果可以发现： 第一， 无限制平流算法的计算误差主要由水平多矩空间离散决定， 具有四阶收敛速度； 第二， 添加水平WENO限制器后， 计算误差和收敛速度未受影响， 说明WENO算法可以很好地识别正弦波这样的光滑流场， 模板加权系数在收敛性试验中可取到精度最优值； 第三， 添加垂直TVD限制器和正定修正后， 算法的收敛性受到一定影响； 第四， 对于同时包含光滑区域和大梯度分布的实际流动， 使用光滑度判据， 有选择地使用限制器是有必要的。

3.1.2　阶梯分布平流测试

计算以下阶梯形分布物理量的平流输送， 检验算法在间断分布附近的保形能力，
q x , z , 0 = 1 , x 2 + z 2 ≤ 0.4 0.5 , x 2 + z 2 ≤ 0.8 0 , 其他
试验中一个周期内的总积分步数取 N t = 10 N x。我们在两种不同分辨率网格上（ N x = 40,80）检验了阶梯分布平流输送的计算结果， 如图4所示。可以看出， 平流算法中采用的保形斜率限制器很好地控制了间断附近的非物理振荡。图5中给出了 N x = 80网格上包含及不包含正定修正时， 数值结果最小值的时间变化。无正定修正时， 数值结果中有小的负值存在（ 10 - 6量级）； 使用正定修正后， 数值结果能够保证非负（机器精度量级）。 此外， 本试验中， 垂直方向CFL数已经超过1， 正定修正需使用本文提出的迭代修正过程， 设置的最大迭代次数为3。
图4 阶梯分布物理量的平流输送计算结果

Fig.4 Numerical results of advection test of a step-shaped distribution

图5 阶梯分布物理量的平流输送计算结果中最小值的时间演变（ N x = 80）

Fig.5 Time history of minimum value in advection test of a step-shaped distribution （ N x = 80）

3.2　球面二维（ θ - z）平流试验

基于经纬网格的球面三维通量型平流方程可写为
∂ J ρ q ∂ t + ∂ u J ρ q ∂ λ + ∂ v J ρ q ∂ θ + ∂ w J ρ q ∂ z = 0，
式中： ρ为空气密度； q为输送量含量； J = a 2 c o s θ为坐标变换的雅科比； λ , θ为经纬度； z为海拔； a为地球半径； u , v为水平速度矢量（角速度）； w为垂直速度。
Kent et al （2014）中提出了一个可简化为球面二维（ θ - z）试验的类哈德莱经向环流算例。算例中密度不随时间发生变化， 其空间分布由处于静力平衡的等温大气给出。算例中所有变量均与 λ无关， 控制方程中第二项为零， 试验可简化为二维问题（用非经纬网格模式测试此算例时， 二维与三维试验的等价性依赖于具体的离散格式）。随时间变化的速度场 v , w具有以下形式
v θ , z , t = - w 0 π ρ 0 K z t o p ρ c o s   θ s i n   K θ c o s   π z z t o p c o s   π t τ w θ , z , t = w 0 ρ 0 K ρ [ - 2 s i n   K θ s i n   θ + K c o s   θ c o s   K θ ] s i n   π z z t o p c o s   π t τ
输送量的初始分布只与海拔相关， 具有余弦钟形分布
q z = 1 2 1 + c o s   2 π z - z 0 z 2 - z 1 z 1 < z < z 2 0 其他
试验中各种参数的选取与Kent et al （2014）保持一致。
由于本算例的初始条件包含光滑极值， 为保证计算精度， 需对限制器的使用进行优化（Durran， 2010）。简单起见， 本算例中限制器只在输送量值接近零（小于0.02）的计算单元内使用。对于更加复杂的实际流动， 可以引入光滑指示器（smoothness indicator）来识别需要进行限制的计算单元， 如： 我们前期研究中采用的基于WENO思想的光滑指示器（Huang et al， 2021）。
图6所示为两种分辨率网格 ( N θ × N z=90×60和180×120）上的数值仿真结果。在仿真计算的前半段， 输送量自初始分布开始变形， 在 t = 12   h T 2时， 变形达到最大程度； 随后输送量分布逆向恢复， 最终在 t = 24   h时返回其初始分布。同Kent et al （2014） 给出的参考解相比， 本文提出的平流算法准确复现了输送量分布的时间演变过程。比较疏密网格上的计算结果， 随网格分辨率提高， 最终计算结果更加接近初始分布， 数值仿真精度得到改善。
图6 类哈德莱经向环流算例计算结果

Fig.6 Numerical results of Hadley-like meridional circulation

在 0.5 ° × 100   m（ N θ × N z=180×120）网格上， 数值仿真结果的归一化误差为 l 1 = 1.17 × 10 - 2， l 2 = 1.39 × 10 - 2， l ∞ = 3.24 × 10 - 2， 与Kent et al （2014）和Tang et al （2022）中CAM-FV和MCV3-BGS-PRM平流模式具有相当的计算精度。

4 结论与展望

本文发展了一套新的大气平流方程高精度计算方案。该方案基于多矩非静力大气动力框架（Chen et al， 2023）采用的混合空间离散格式发展了保形、 正定限制策略， 并使用成对龙格-库塔方法设计了高效的显式时间推进方案。与采用方向分裂策略的MCV3-BGS-PRM平流算法（Tang et al， 2022）相比， 新算法与模式动力过程计算更为协调， 能避免平流输送过程仿真的散度误差。与现有保形平流算法在光滑区域大多仅有二阶精度（Lauritzen et al， 2014）相比， 本文发展的平流计算格式在水平方向可达四阶收敛， 能有效提高大气输送过程的计算精度。本文完成了垂直二维标准算例测试， 验证了基于所提出算法发展高分辨、 可扩展非静力大气数值模式高保真平流输送计算方案的可行性。
进一步研究工作主要包括： 采用提出算法完成基于立方球网格的三维大气平流方程求解器； 采用成对显式龙格-库塔方法发展新的隐式-显式（implicit-explicit， IMEX）龙格-库塔时间积分方案， 并应用于非静力大气动力框架HEVI时间推进； 结合新发展的大气平流算法和动力框架HEVI时间积分方案， 建立高分辨率条件下大气动力过程与平流输送过程的耦合计算方案。

References

Publishing order | Descend order by publishing year | Descend order by cited within
Arbogas T， Huang C S， Zhao X K， et al， 2020.A third order， implicit， finite volume， adaptive Runge-Kutta WENO scheme for advection-diffusion equations［J］.Computer Methods in Applied Mechanics and Engineering， 368： 113155.DOI： 10.1016/j.cma.2020.113155 .

Blossey P N， Durran D R， 2008.Selective monotonicity preservation in scalar advection［J］.Journal of Computational Physics， 227（10）： 5160-5183.DOI： 10.1016/j.jcp.2008.01.043 .

Chen C G， Li X L， Xiao F， et al， 2023.A nonhydrostatic atmospheric dynamical core on cubed sphere using multi-moment finite-volume method［J］.Journal of Computational Physics， 473： 111717.DOI： 10.1016/j.jcp.2022.111717 .

Collela P， Woodward P R， 1984.The piecewise parabolic method （PPM） for gas-dynamical simulations［J］.Journal of Computational Physics， 54（1）： 174-201.DOI： 10.1016/0021-9991（84）90143-8 .

Durran D R， 2010.Numerical methods for fluid dynamics： with application in geophysics［M］.New York： Springer.DOI： 10.1007/978-1-4419-6412-0 .

Gardner D J， Guerra J E， Hamon F P， et al， 2018.Implicit-explicit （IMEX） Runge-Kutta methods for non-hydrostatic atmospheric models［J］.Geoscientific Model Development， 11（4）： 1497-1515.DOI： 10.5194/gmd-11-1497-2018 .

Huang P， Chen C G， Li X L， et al， 2021.A nonnegative and shape-preserving global transport model on cubed sphere using high-order conservative collocation scheme［J］.International Journal for Numerical Methods in Fluids， 93（6）： 1969-1992.DOI： 10. 1002/fld.4962 .

Ii S， Xiao F， 2009.High Order Multi-moment Constrained Finite Volume Method.Part I： Basic Formulation［J］.Journal of Computational Physics， 228（10）： 3669-3707.DOI： 10.1016/j.jcp. 2009.02.009 .

Kent J， Ullrich P A， Jablonowski C， 2014.Jablonowski， Dynamical core model intercomparison project： tracer transport test cases［J］.Quarterly Journal of the Royal Meteorological Society， 140（681）： 1279-1293.DOI： 10.1002/qj.2208 .

Lauritzen P H， Ullrich P A， Jablonowski C， et al， 2014.A standard test case suite for two-dimensional linear transport on the sphere： results from a collection of state-of-the-art schemes［J］.Geoscientific Model Development， 7： 105-145.DOI： 10.5194/gmd-7-105-2014 .

Li X L， Shen X S， Chen C G， et al， 2020.A note on non‐negativity correction for a multimoment finite‐volume transport model with WENO limiter［J］.Quarterly Journal of the Royal Meteorological Society， 146（726）： 546-556.DOI： 10.1002/qj.3675 .

Smolarkiewicz P K， 1989.Comment on “A positive definite advection scheme obtained by nonlinear renormalization of the advective fluxes”［J］.Monthly Weather Review， 117（11）： 2626-2632.DOI： 10.1175/1520-0493（1989）117<2626： COPDAS>2.0.CO； 2 .

Sun Z Y， Teng H H， Xiao F， 2015.A slope constrained 4th order multimoment finite volume method with WENO limiter［J］.Communications in Computational Physics， 18（4）： 901-930.DOI： 10. 4208/cicp.081214.250515s .

Tang J， Chen C G， Li X L， et al， 2018.A non-oscillatory multimoment finite-volume global transport model on a cubed-sphere grid using the WENO slope limiter［J］.Quarterly Journal of the Royal Meteorological Society， 144（714）： 1611-1627.DOI： 10.1002/qj.3331 .

Tang J， Chen C G， Shen X S， et al， 2022.A three-dimensional positivity-preserving and conservative multimoment finite-volume transport model on a cubed-sphere grid［J］.Quarterly Journal of the Royal Meteorological Society， 148（749）： 3622-3638.DOI： 10.1002/qj.4377 .

Vermeire B C， 2019.Paired explicit Runge-Kutta schemes for stiff systems of equations［J］.Journal of Computational Physics， 393： 465-483.DOI： 10.1016/j.jcp.2019.05.014 .

Weller H， Lock S J， Wood N， 2013.Runge-Kutta IMEX schemes for the Horizontally Explicit/Vertically Implicit （HEVI） solution of wave equations［J］.Journal of Computational Physics， 252： 365-381.DOI： 10.1016/j.jcp.2013.06.025 .

Williamson D， Drake J， Hack J J， et al， 1992.A standard test set for numerical approximations to the shallow water equations on the sphere［J］.Journal of Computational Physics， 102（1）： 211-224.DOI： 10.1016/S0021-9991（05）80016-6 .

Xiao F， Yabe T， 2001.Completely conservative and oscillation-less semi-Lagrangian schemes for advection transportation［J］.Journal of Computational Physics， 170（2）： 498-522.DOI： 10.1006/jcph.2001.6746 .

Options
Outlines

/

〈 〉

The system is designed and developed by Beijing magtec Technology Development Co., Ltd. with technical support: support@magtech.com.cn