Plateau Meteorology

Plateau Meteorology >

2025 , Vol. 44 >Issue 2: 445 - 461

DOI: https://doi.org/10.7522/j.issn.1000-0534.2024.00074

Application of Hilbert Huang Transform Method Based on CEEMD in Forest Boundary Layer Turbulence

  • Yanqi WANG ,
  • Yu ZHANG ,
  • Youqi SU ,
  • Qian ZHANG ,
  • min YE
Expand
  • College of Atmospheric Sciences，Chengdu University of Information Technology /Chengdu Plain Urban Meteorology and Environment Sichuan Provincial Field Scientific Observation and Research Station，Chengdu 610225，Sichuan，China

Received date: 2024-03-19

  Revised date: 2024-07-01

  Online published: 2024-08-30

Copyright

© Editorial Department of Plateau Meteorology （CC BY-NC-ND）
Fold

Abstract

To address the modal aliasing phenomenon in traditional Empirical Mode Decomposition （EMD） algorithms， the Complementary Ensemble Empirical Mode Decomposition （CEEMD） and Mirror Extension algorithm were introduced to improve the shortcomings in EMD algorithm decomposition.This article selects case data from turbulence observations in the artificial forest area of Mount Si'e.Firstly， the differences between the two methods are compared and analyzed to clarify the advantages of the CEEMD algorithm； Then， case data of stable and unstable layers at different heights were selected， and the Hilbert Huang transformation method was applied to analyze the turbulent characteristics of the wind speed U and temperature T series under this case， exploring the application of the Hilbert Huang transformation method.The results indicate that the algorithm decomposition of CEEMD is more detailed， the mode aliasing defect of the modal function is better suppressed， the modal energy distribution is more focused， the Hilbert marginal spectrum has more energy spikes， and the energy distribution is clearer.Different modal functions have their own characteristic frequencies， and the decomposed modal functions contain motion of different scales， including turbulent motion in the inertial sub region with a slope of -2/3， and low-frequency large-scale modes corresponding to the energy containing region.The marginal spectral energy peaks obtained from CEEMD decomposition well reflect the energy containing characteristics of each modal function.Individual case analysis shows that the CEEMD algorithm can act as a typical binary filter.After CEEMD decomposition， there are gust fluctuations of about 3~6 minutes in the various modal functions of the U-wind in the turbulence signal of this case.The turbulence characteristics vary at different heights and stable layers.The Hilbert marginal spectral amplitude is higher in the unstable layer at noon compared to the stable layer at night， and the three-dimensional wind speed is better mixed at various heights.Moreover， due to the effect of the canopy， there is a crushing effect on large-scale turbulent vortices at lower altitudes， and the marginal spectrum exhibits low frequency small and high frequency large characteristics compared to other altitudes.In this case， the temperature T is different from the three-dimensional wind speed performance： turbulent vortices at different altitudes are better mixed under stable layer structures， while under unstable layer structures， the marginal spectrum amplitude at lower altitudes is higher due to differences in thermal absorption at different altitudes， and decreases with increasing altitude.Overall， this comparative analysis highlights the superior capabilities of the CEEMD algorithm in handling complex turbulence data， ensuring a more precise and insightful examination of atmospheric phenomena.

Key words： Hilbert Huang; CEEMD; turbulence; forest underlying surface; mirror extension

Cite this article

Yanqi WANG , Yu ZHANG , Youqi SU , Qian ZHANG , min YE . Application of Hilbert Huang Transform Method Based on CEEMD in Forest Boundary Layer Turbulence[J]. Plateau Meteorology, 2025 , 44(2) : 445 -461 . DOI: 10.7522/j.issn.1000-0534.2024.00074

1 引言

大气边界层主要指的是离地高度为1~2 km的大气层， 在大气边界层中湍流运动是主要运动形式。湍流运动具有多尺度、 不规则、 混合性等多种特征。同时， 边界层湍流在大气边界层中的动量、 热量等物质和能量交换中扮演着重要角色（Haugen et al， 1971； Cava and Katul， 2008； Steiner et al， 2018； Mauder et al， 2020）， 对人类生产生活有着巨大的影响（杨斌等， 2022； 张强等， 2022； 范德民等， 2024）。
由于湍流的多尺度特征， 传统的统计学方法-傅里叶能谱分析在湍流研究中有着重要地位。如著名的 Kaimal et al（1972）实验就是基于傅里叶谱分析了湍流的结构特点证实了在惯性副区满足Kolmogorov（1968）理论并给出了相应的拟合公式。国内学者也基于传统的傅里叶谱分析方法对不同下垫面的大气湍流运动的普遍规律和特殊性进行了研究（刘和平等， 1997； Zhang et al， 2010； 金莉莉等， 2019）， 如刘和平等（1997）利用谱分析在森林下垫面研究了冠层上下的湍流的结构特征差异。此后， 小波变换这类时频分析方法得到发展， 对边界层湍流的研究得以在时频域共同展开， 许多学者利用小波变换对湍流的进行了更深入的研究（Lu and Fitzjarrald， 1994； Thomas and Foken， 2005； 全利红等， 2007； 白士伟等， 2018）。如利用小波变换计算相干结构通量贡献并分析通量的传输效率（Barthlott et al， 2007； Zhang et al， 2011）。
但是， 以上传统的时频分析方法都存在一定的缺陷， 基于傅里叶变换的频谱分析其对应的频率段是基于整个时间段， 对于线性不稳定， 非均匀变化的信号而言无法确定其对应的发生时刻， 会引入虚假的频率成分； 小波分析虽然能在时域和频域上共同展开， 但是对于非线性信号的分解仍然存在局限性， 且不同的小波基函数的选取可能会产生较大的结论差异， 对实验研究产生一定的不确定性。大气边界层湍流是一种非平稳、 非线性信号， 上述分析方法多存在一定的局限性（卢志明等， 2006； 张汉九等， 2022）。
希尔伯特-黄变换算法（Hilbert-Huang Transform， HHT）是一种自适应、 非先验的、 信号分解完全基于数据驱动的一种方法。该方法的第一个环节是经验模态分解（Empirical Mode Decomposition， EMD）， 时间序列经过EMD分解后可以得到本征模态函数（Intrinsic Mode Function， IMF）， 然后对EMD后的各IMF做希尔伯特变换， 可以得到三维希尔伯特谱， 该方法对处理分析非稳态， 非线性的数据有巨大优势， 近年来被国内外学者广泛应用于各个领域。如利用HHT分析降水、 风场、 气旋、 台风等常见气象要素特征（Vincent et al， 2010； 任冉， 2014）。在海洋领域， 也有学者利用HHT对海洋的现象进行研究（Wang et al， 2013； Martins et al， 2017； 姜浩等， 2018）。
在传统HHT方法中， 其核心环节EMD有一定的缺陷， 其一就是模态混叠， 其二就是端点效应。为了解决第一个缺陷Yeh et al（2011）提出了一种EMD的改进方法称为互补集合经验模态分解（Complementary Ensemble Empirical Mode Decomposition， CEEMD）其主要原理是在信号中加入随机的互为相反数的高斯白噪声经多次平均后来限制EMD方法中存在的模态的混叠现象。针对第二个缺陷， 镜像延拓法可以用来解决序列分解中存的端点效应， 本文基于两种方法对传统HHT方法进行改进。
鉴于HHT方法在大气边界层湍流中的应用报道较少且多基于传统的EMD方法（Zhu et al， 2016； Gao et al， 2017； Wei et al， 2018）， CEEMD方法在非平稳时间序列研究中具有优势， 本文基于四川省乐山市四峨山森林下垫面不同高度的湍流观测数据， 选取个例数据， 首先对比EMD和CEEMD方法在HHT中的区别， 明确CEEMD方法的优势； 然后再选取不同高度、 不同稳定度条件下的个例数据， 应用基于CEEMD的希尔伯特黄变换算法分析该个例下的湍流特征， 探讨和分析HHT方法在边界层湍流中的应用。

2 资料选取与方法介绍

2.1　资料选取及处理

观测地点位于四川省乐山市四峨山人工森林地区（103.47°E， 29.66°N）， 森林平均冠层高约为15 m， 观测场内架设了一60 m高度的观测塔（图1）， 在0.13、 0.67、 1.06、 1.33、 1.67、 2.0、 2.53、 3.87倍冠层高度的位置架设了风（WindSonic， Gill， UK）、 温、 湿（HMP155A， Vaisala， Helsinki， Finland）梯度观测， 在1.33、 2.53、 3.86倍冠层高度的位置架设了3套涡动相关系统（IRGASON， Campbell Scientific， USA）， 分别观测位于森林下垫面粗糙副层内（20 m高度）、 粗糙副层与常通量层交界（38 m高度）、 常通量层（56 m高度）三个高度的湍流数据， 仪器采样频率为10 Hz（常娜等， 2022）。
图1 四峨山森林气象观测塔

Fig.1 Forest meteorological observation tower of Mount Sie

本文首先选取了2021年5月7日12:00（北京时， 下同） -12:30位于20 m高度的观测数据， 分别采取基于EMD的 HHT方法和CEEMD的HHT的方法对比分析方法的谱图表现差异， 明确CEEMD方法的优势； 然后基于CEEMD方法的HHT， 选取2021年5月16日00:00 -00:30午夜时段和12:00 - 12:30正午时段三个高度的（20 m、 38 m、 56 m）的湍流观测数据， 分别对该个例下的标量温度 T和三维矢量风速中的水平风速的 u湍流结构特征进行分析， 两个时段的数据分别代表了三个高度从午夜的稳定层结发展到正午时不稳定层结时的特征（选取的数据湍流发展相对平稳， 数据无缺失， 满足谱分析完整性和连贯性的特点）。湍流观测数据在原始观测数据的基础上， 经过了野点去除、 坐标旋转等必要的预处理流程（王少影等， 2009； 王咏薇等， 2013）。

2.2　方法介绍

（1） 希尔伯特变换
针对非平稳、 非线性的湍流信号， 频率时刻会发生突变， 此时根据傅氏变换定义的全局频率有一定的虚假分量， 失去了本身的物理意义， 所以需要用瞬时频率这一物理量来描述不稳定信号。关于瞬时频率的定义有多种， 目前对于瞬时频率的定义主要是基于Gabor（1946）提出的基于解析信号的瞬时频率的定义。Gabor对于原信号 c ( t )的解析信号 z t定义为：
z t = c t + j 1 π P V ∫ - ∞ + ∞ c τ t - τ d τ
式中： PV代表柯西主值， 该解析信号的虚部的定义用到了原信号的希尔伯特变换（Hilbert Transform）， 与信号的希尔伯特变换表达式一致。希尔伯特变换是一个幅值不变的全通滤波器， 定义了实部与虚部的关系， 原信号的希尔伯特变换 H [ c ( t ) ]定义为：
y ^ t = H c t = 1 π P V ∫ - ∞ + ∞ c τ t - τ d τ
可以看到式（2）与式（1）的虚部定义一致。式（1）和式（2）以无穷为时间积分， 但在该方法的实际应用中绝大多数都以有限时间的时间序列为研究对象， 本文以30 min序列为例， 讨论该方法在湍流中的实际应用效果并加以探讨研究。由此利用希尔伯特变换在解析信号的基础上可以求得信号的瞬时频率。但是边界层湍流这类时序信号多为复合信号， 对其作希尔伯特变换可能会产生负频率， 不具有物理意义。作希尔伯特变换的信号必须是单分量信号， 也即某一时刻只能有一个确定的频率值与之对应。所以在作希尔伯特变换之前必须要将原始湍流信号分解， 故而黄鄂在提出了分解方法-EMD。
（2） EMD算法
Huang et al（1998）提出的EMD算法将原始湍流信号分解为多个单分量信号的线性组合IMF， 这些IMF对于希尔伯特变换来说是有物理意义的。
Huang认为任何一个时序信号都可以分解为多个IMF， 并认为若一个函数满足如下定义则可以被称作IMF：
（1） 在整个数据段内， 极值点的个数和过零点的个数必须相等或者相差最多不超过一个。
（2） 在任意时刻， 由极大值形成的上包络线和极小值形成的下包络线平均值为零。包络线在时间轴保持局部对称。
经过迭代分解后原始信号 u t可以写为多个IMF与残差 r n t之和也即
u t = ∑ i = 1 n - 1 i m f i t + r n t
对每个 x i ( t ) = i m f i ( t )就可以做希尔伯特变换 H ( x i ( t ) )得到解析信号的虚部由 x ^ i ( t )此得到解析信号
z i t = i m f i t + j H i m f i t = x i t + j x ^ i t = A i t e j θ i t
A i ( t )和 θ i ( t )分别代表瞬时振幅和瞬时相位， 其表达式为：
A i t = x i 2 t + x ^ i 2 t
θ i t = a r c t a n x ^ i t x i t
由此可以求得瞬时频率：
ω i t = d θ i t d t
由上述三个参量可以得到时间-频率-振幅的三维希尔伯特谱即 H ( ω , t )， 将三维希尔伯特图沿时间维积分可以得到希尔伯特边际谱其定义为：
h ω = ∫ 0 T H ω , t d t
这里需要明确的是， 希尔伯特边际谱与传统的傅里叶频谱虽然也是频率-振幅分布但是代表的物理意义截然不同。傅里叶频谱的基函数为正余弦简谐波为基， 且基函数遍布整个时域空间。而边际谱的频率和幅值实际上是在整个时间域上某一特定频率发生的幅值的积分， 某一频率在边际谱幅值较高则说明该频率发生概率较大， 是一种加权的联合幅值-频率-时间分布图（Huang et al， 1998）。
结合Huang et al（1998）提出的EMD分解和Hilbert变换， 可以对湍流时间序列的信息进行更好的分析。
（3） CEEMD方法与镜像延拓法
EMD方法中存在的第一个缺陷就是模态混叠（Modal Aliasing）， 所谓模态混叠现象分为两种情况， 一种情况就是不同特征尺度的信号在同一个IMF中出现， 另一种情况就是同一个特征尺度的信号分散到了不同的IMF信号中（Wu and Huang， 2004）。
针对EMD方法的缺陷， 出现了很多类EMD算法， 包括通过加入白噪声进行集合平均的集合经验模态分解（Ensemble Empirical Mode Decomposition， EEMD）， 但是EEMD算法中存在有白噪声的残余， 对分解结果有一定的影响。互补集合经验模态分解CEEMD方法在EEMD的基础上通过添加互补的白噪声， 减少了白噪声对结果的影响， 从而形成更精准的包络线， CEEMD算法是类EMD算法中较新的一种算法（Yeh et al， 2011； Colominas et al， 2014）。
EMD方法中还存在有另一个缺陷， 即端点效应， 在信号端点附近会由于包络线插值的发散而带来分解误差， 并会逐步向信号内传播， 污染整个时间序列， 对低频模态而言这种现象更为显著。镜像延拓法的原理简单来说就是利用镜面对称的特点在信号端点的极值点处安放一面镜子， 利用镜面对称的特点， 将镜内信号的极值点通过镜像对称， 向镜面外延伸极值点， 从而避免端点效应。具体过程请参考文献（肖瑞等， 2018； 马中存和肖全山， 2019）。

3 结果分析

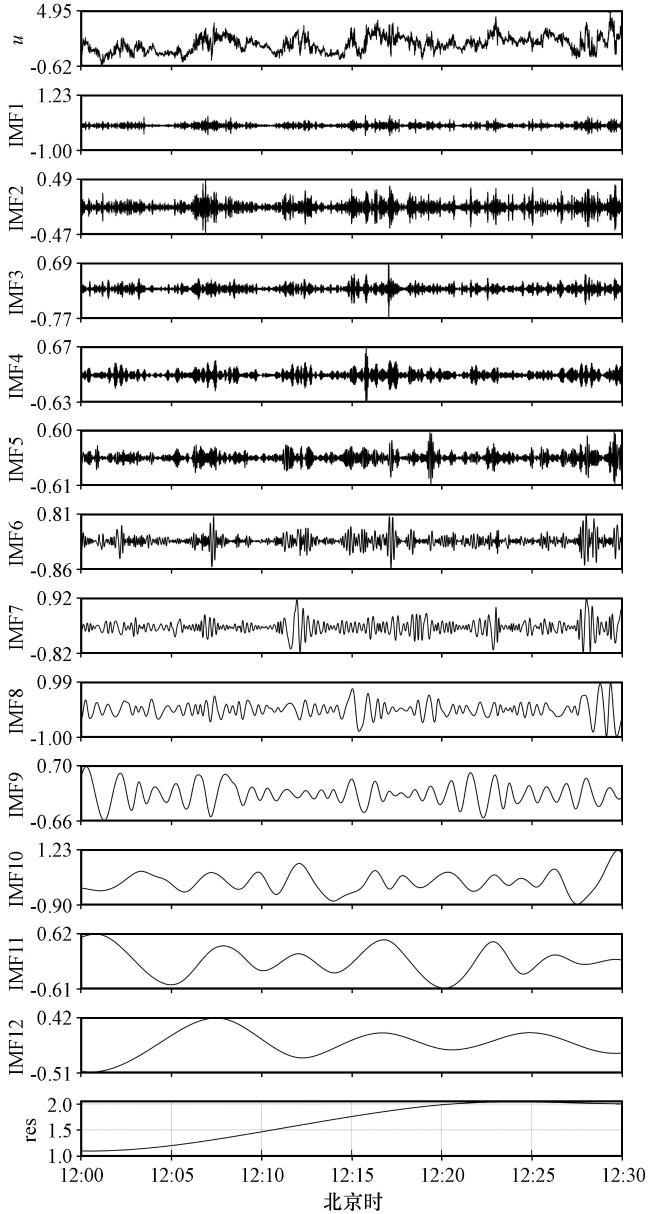
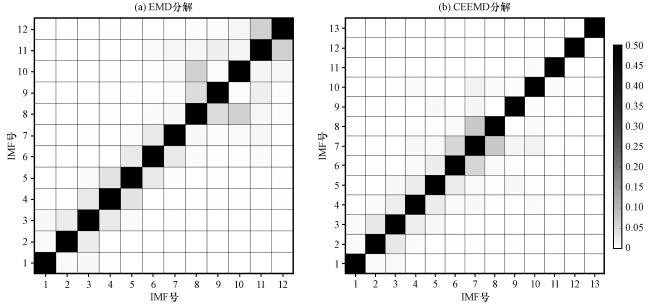
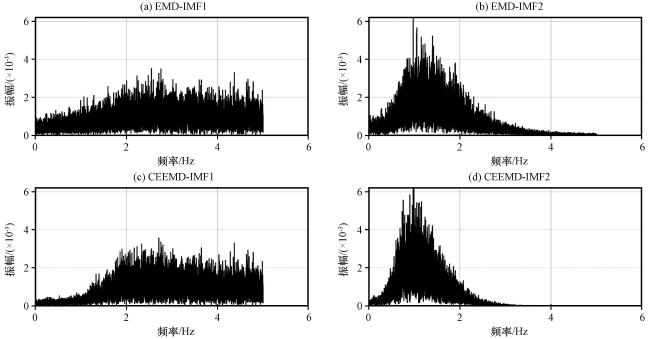
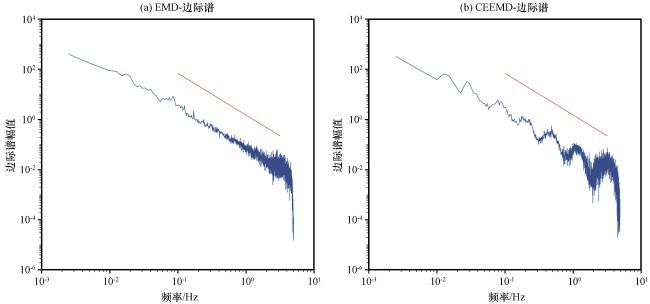
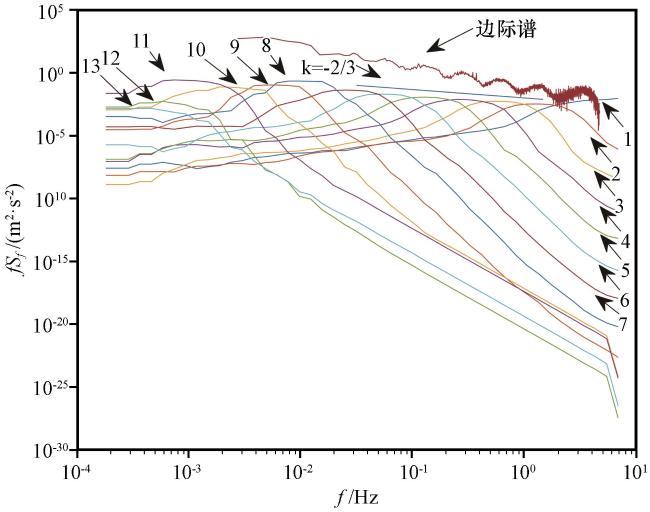
3.1　基于CEEMD算法与EMD算法的HHT对比分析

本节利用2021年5月7日12:00 -12:30， 位于观测场地20 m高度处的半小时湍流观测数据， 以水平 u风为例， 对比基于EMD方法和CEEMD方法的HHT的谱图差异， 以明确CEEMD方法的优势。
图2给出了水平 u风序列经EMD分解后的各模态函数， 共分解得到了12个本征模态函数和1个残差项res， 分解得到的IMF1所代表的频率最高， 振荡最剧烈， 代表着湍流中最高频的小尺度成分， 随着分离模态阶数的增加， 频率减小， 波动周期变长， 残差项代表了整个序列的发展趋势， 后文中的三维希尔伯特图和边际谱均不考虑此趋势项， 以达到去趋势的目的。
图2 2021年5月7日12:00 -12:30水平 u风的EMD分解

Fig.2 EMD decomposition of horizontal u-wind from 12:00 to 12:30 on May 7， 2021

为对比分析， 图3给出了该时次湍流信号经镜像延拓后CEEMD分解的各模态函数， 与EMD分解相比CEEMD分解有所不同， 共分解出了13个IMF和一个残差项。表1给出各模态函数能量占比， CEEMD分解的波动能量主要集中在IMF1-IMF10中， IMF11-IMF13的波动能量相对很小， CEEMD分解的波动能量在IMF1-IMF9比EMD分解的能量占比更大， 这说明CEEMD分解的各个尺度的IMF能量分布更向前几个IMF集中， 这是因为CEEMD分解的白噪声的加入使得信号极值点分布更加均匀， 从而在筛选不同尺度的IMF过程中可以更好的使不同尺度的信号集中分布到对应尺度的模态中， 减少了不同尺度信号的模态混叠， 使得各尺度的模态能量更加向前集中（Wu and Huang， 2004， 2009）。
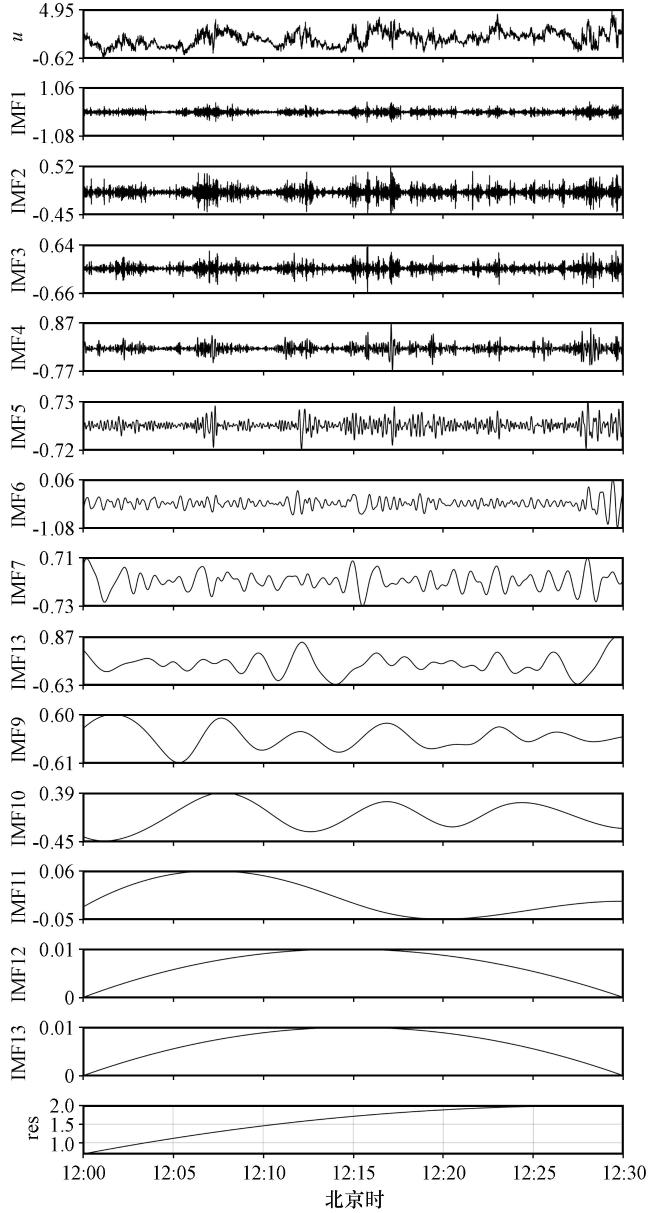
图3 2021年5月7日12:00 -12:30水平 u风的CEEMD分解

Fig.3 EMD decomposition of horizontal u-wind from 12:00 to 12:30 on May 7， 2021

表1 EMD分解与CEEMD分解各模态能量占比

Table 1 Energy proportion of each mode in emd decomposition and CEEMD decomposition

IMF阶数 EMD分解能量占比/% CEEEMD分解能量占比/%
1 0.87 1.11
2 0.90 1.17
3 1.16 2.08
4 1.46 4.26
5 2.13 5.93
6 5.28 12.08
7 8.12 16.16
8 13.89 20.51
9 12.27 20.75
10 26.89 15.29
11 17.82 0.59
12 9.21 0.03
13 - 0.03
为了量化EEMD对EMD方法的模态混叠缺陷的改进， Huang et al（2008）定义了一个全局正交性指数 I O T和两个IMF之间的局部正交性指数 I O j k， 该指数越小则说明正交性越好， 也即模态混叠程度更小（Huang et al， 2008； Chen et al， 2012）， 其表达式分别为：
I O T = ∑ t   ∑ j = 1 j ≠ k n + 1   ∑ k = 1 n + 1   i m f j t i m f k t ∑ t   u 2 t
I O j k = ∑ t i m f j t i m f k t ∑ t i m f j 2 t + i m f k 2 t
除正交性指标外， EMD分解还有一个完备性的概念， 完备性指的是信号分解后再次重构回原信号的能力， 可以采用重构后的信号与原信号的均方根误差来衡量（司友强等， 2019）。表2给出了两种方法的全局正交指数和均方根误差。对比来看， CEEMD的全局正交性指数优于EMD， 这说明该方法对模态混叠现象有所抑制， 并且两种方法的均方根误差均非常小， 可以认为两种方法的完备性都有很好的效果， 但相对来讲CEEMD方法的完备性指标更好。图4给出了局部正交性指数图， 从图中可以看到， EMD分解在非对角线处存在有更多的非0元素， 在IMF9和IMF8， IMF10和IMF8， IMF12与IMF11都存在一定程度的模态混叠， 而CEEMD分解压制了这种模态混叠现象， 局部正交性相对更好。
表2 EMD与CEEMD分解指标比较

Table 2 Comparison of EMD and CEEMD decomposition indicators

分解方法 正交指数 均方根误差
EMD 0.0749 3.191×10-16
CEEMD 0.0512 3.178×10-16
图4 EMD分解和CEEMD分解局部正交性检验

Fig.4 EMD decomposition and CEEMD decomposition local orthogonality test

利用傅里叶变换， 可以从频率角度研究模态混叠现象。图5分别给出了EMD和CEEMD的分解后的IMF1和IMF2的频谱图。如图5所示， 两种方法分解的IMF1频谱差距不大而 CEEMD分解的IMF2的频带分布较EMD分解的IMF2频带分布更集中， 同样说明CEEMD分解的IMF1和IMF2之间的频率分离更好， 模态混叠现象有所改善， 这种改善在其他阶模态中仍有体现， 以相对高频的IMF1和IMF2最为明显。
图5 EMD分解和CEEMD分解后频谱图

Fig.5 Spectrum after EMD decomposition and CEEMD decomposition

将以上各IMF做希尔伯特变换并积分时间维度可以得到频率-振幅分布的边际谱。图6展示了EMD和CEEMD两种方法分解后的边际谱特征， 可以看到CEEMD和EMD方法的边际谱相似， 振幅能量主要集中在低频的大尺度湍涡中， 由于能量级串效应， 能量不断向高频小尺度湍涡传递， 最后通过分子黏性作用， 将能量耗散。但是， 区别于EMD的边际谱， 两种方法的边际谱在惯性副区均表现出了湍流傅里叶谱中存在的-5/3斜率的惯性副区特征， 而且CEEMD的边际谱存在更多的谱峰， 能够更好地捕捉到湍涡能量传递过程中的含能湍涡及对应的湍涡尺度。
图6 EMD和CEEMD分解后的边际谱（直线斜率为-5/3）

Fig.6 Marginal spectr after EMD and CEEMD decomposition （with a slope of -5/3）

为了探究CEEMD分解后边际谱和各模态函数的傅里叶频谱的关系， 图7给出了各模态函数的傅里叶频谱图和对应的边际谱图， 从图7中可以看到， CEEMD分解得到的各模态函数都有自己的峰值频率， 第一个模态IMF1频率最高， 它代表着湍流中最小尺度的运动， 也有可能是环境中存在的高频噪音； 模态IMF2-IMF7对应着-2/3斜率， 与惯性副区的-2/3律相同， 它们代表着湍流中惯性副区的成分； 模态IMF8-IMF13对应着低频尺度湍涡， 他们含能较多， 频率也较低， 对应着含能区的湍涡， 这一结论与一些研究结果类似（Huang et al， 2007； Wang et al， 2013）。
图7 CEEMD后分解各模态函数的傅里叶频谱图和边际谱直线斜率为-2/3

Fig.7 Fourier spectrum and marginal spectrum of each modal function after CEEMD decomposition.Straight line slope -2/3

从图6（b）和图7中可以看到CEEMD的边际谱中都出现了起伏的峰值， 而EMD分解不存在峰值。图7中的边际谱峰值与一些模态函数的傅里叶谱峰值频率大致呈出对应相等的关系。从这个角度来看， 这些峰值出现的原因可能如前文所述， 是因为CEEMD算法对模态混叠的压制导致模态能量更集中， 边际谱从模态函数中 可以更清晰地提取各模态的频率-能量关系， 从而出现了更多的峰值。

3.2　基于CEEMD的HHT方法的边界层湍流个例分析

上文的对比分析展示了CEEMD方法对于EMD方法的希尔伯特-黄变换在边界层湍流分析中的区别与优势。本节选取2021年5月16日00:00 - 00:30和12:00 -12:30， 分别位于观测场地20 m、 38 m和56 m高度处的半小时湍流观测数据， 分别代表了三个高度从夜晚稳定层（00:00 -00:30， 稳定度从低处到高处分别为： 0.7， 0.45， 0.92）发展为正午时不稳定层结（12:00-12:30， 稳定度从低处到高处分别为： -0.34， -0.8， -0.9）的过程， 分别以矢量-水平风速 u和标量-温度 T为例， 应用基于CEEMD的HHT方法对该个例下的湍流特征进行分析， 探讨HHT方法在边界层湍流的应用。
图8和图9分别给出了夜晚稳定条件时水平风速 u和温度 T的CEEMD分解。不同高度的风速 u（图8）的IMF特征表现出了一定的差异： 在00:00 - 00:15， 三个高度的原始 u风序列在该时段振幅都较大， 但在该时段20 m和38 m高度处相对高频的IMF1-IMF5振幅波动明显大于56 m处， 可以认为这两个高度的 u风湍涡主要由高频成分组成， 说明此时较低的高度（20 m和38 m） u风湍涡以小尺度湍涡为主。同样， 温度的IMF（图9）与风速 u的IMF表现出了类似的特征： 在00:00 -00:15， 20 m处的IMF1-IMF5 的模态振幅波动比38 m和56 m处振幅波动稍显剧烈， 说明此时热力湍涡在较低高度相比较高高度主要由小尺度涡组成。 可以看到， CEEMD算法可以自适应的从原始信号中提取不同时间尺度的信息， 且很好的保留了不同尺度上时域的信息。这是由于基函数（IMF）的分离是从原信号的本身特征出发， 从而能够分析出湍流内部的一些特征， 这在边界层湍流这类非定常时间序列的分析中有着很好的适用性。
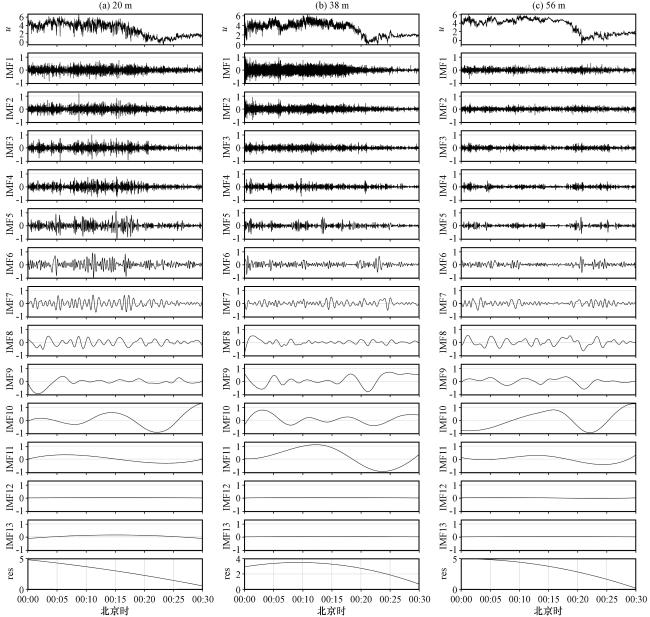
图8 2021年5月16日00:00 -00:30夜晚稳定条件下， 20 m（a）、 38 m（b）、 56 m（c） u风的CEEMD分解

各IMF纵坐标范围与IMF1保持一致

Fig.8 CEEMD decomposition of 20-metre （a）， 38-metre （b）， 56-metre （c） u-wind under stable conditions at night from 00:00 to 00:30 on May 16， 2021.The vertical coordinate range of each IMF is consistent with IMF1

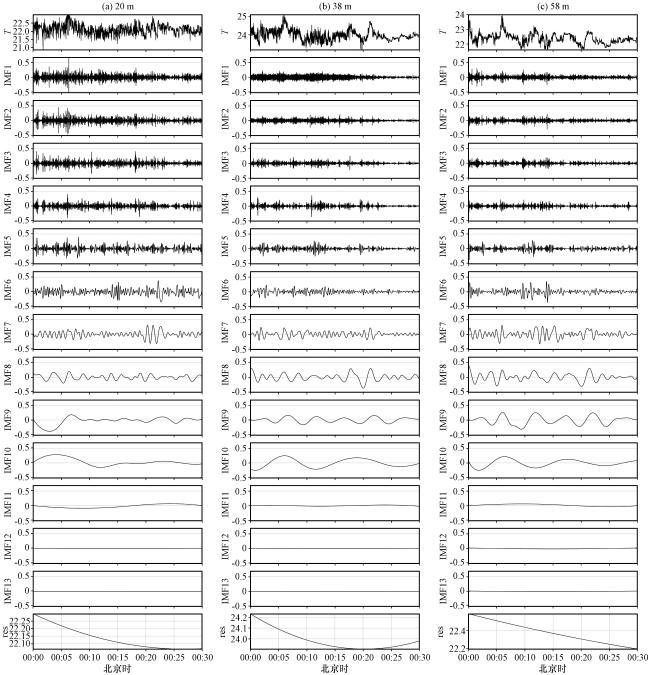
图9 2021年5月16日00:00 -00:30夜晚稳定条件下， 20 m（a）、 38 m（b）、 56 m（c）温度 T的CEEMD分解

各IMF纵坐标范围与IMF1保持一致

Fig.9 CEEMD decomposition of 20-metre （a）， 38-metre （b）， 56-metre （c） temperature under stable conditions at night from 00:00 to 00:30 on May 16， 2021.The vertical coordinate range of each IMF is consistent with IMF1

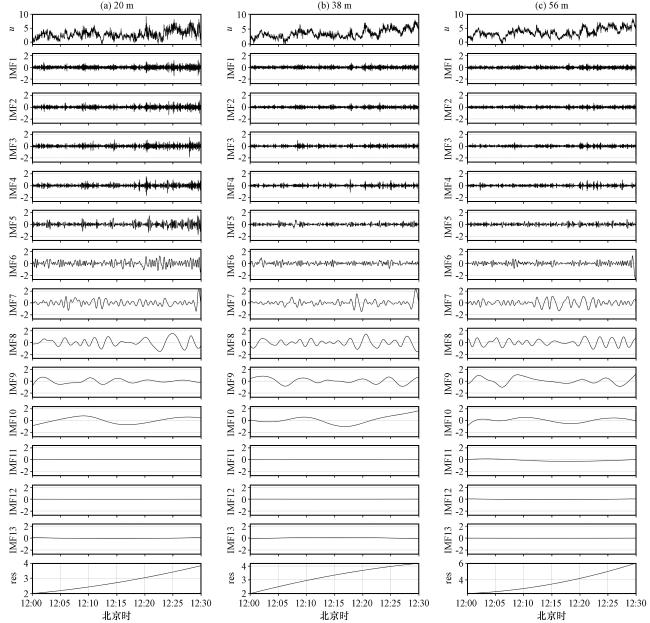
图10和图11分别给出了不稳定条件时水平风速 u和温度 T的CEEMD分解， 不稳定条件下风速 u（图10）， 与稳定层结下相比可能由于对流作用的发展， 各高度IMF没有表现出太大的差异， 各时段IMF振幅分布比稳定层结下更为均匀。但仍能看到在12:20 -12:30， 20 m高度处 u风的相对高频的IMF1-IMF5模态振幅比38 m和56 m的稍大， 说明此时20 m高度处 u风高频小尺度湍涡仍比其他两个高度占优。然而， 在不稳定条件下， 由于正午热力作用的发展， 温度 T的IMF与水平速度 u的表现有差异（图11）： 在较低高度（20 m）处的高频IMF1-IMF5振幅波动整体要比较高高度（38 m和56 m）的振幅波动要大， 说明不稳定条件下由于各层的热力吸收差异， 较低高度的小尺度热力湍涡发展更为充分。
图10 2021年5月16日12:00 -12:30正午不稳定条件下， 20 m（a）、 38 m（b）、 56 m（c） u风的CEEMD分解

各IMF纵坐标范围与IMF1保持一致

Fig.10 CEEMD decomposition of U-winds at 20-metre （a）， 38-metre （b）， and 56-metre （c） under unstable conditions at noon from 12:00 to 12:30 on May 16， 2021.The vertical coordinate range of each IMF is consistent with IMF1

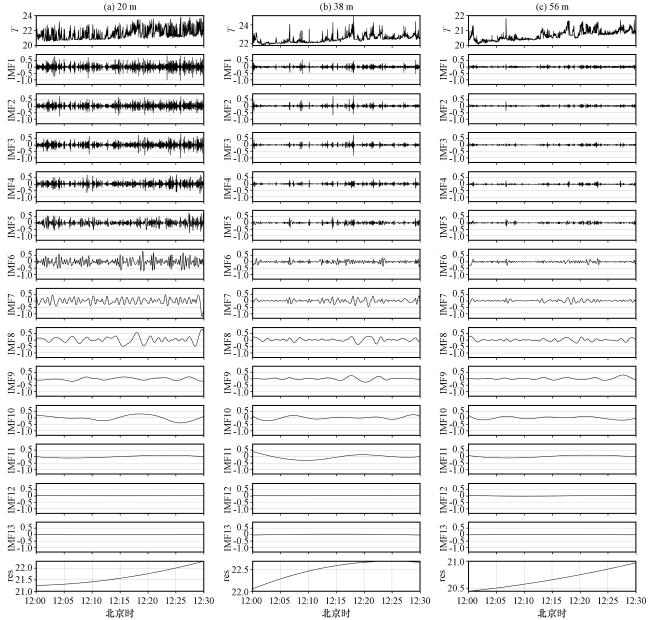
图11 2021年5月16日12:00 -12:30正午不稳定条件下， 20 m（a）、 38 m（b）、 56 m（c）温度 T的CEEMD分解

各IMF纵坐标范围与IMF1保持一致

Fig.11 CEEMD decomposition of temperature T at 20-metre （a）， 38-metre （b）， and 56-metre （c） under unstable conditions at noon from 12:00 to 12:30 on May 16， 2021.The vertical coordinate range of each IMF is consistent with IMF1

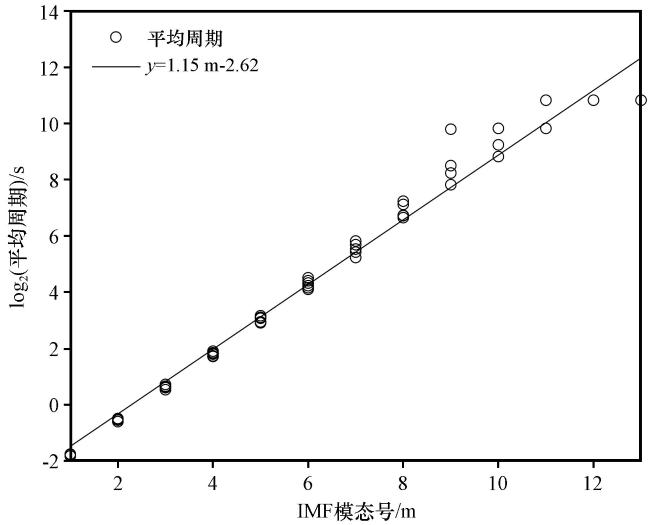
为了更明确各模态函数的特征， 表3分别以水平风速 u计算了在不同稳定度条件下的各模态函数的平均周期（温度 T类似）， 表中各模态平均周期均呈增大趋势， 其中不同稳定层结下的IMF9都有着3~6 min的波动周期， 这与频谱分析中周期为3~6 min的阵风相对应， 代表着湍流中存在的阵风（程雪玲等， 2007）， 该结果与魏伟和张宏升（2013）的边界层湍流研究结果相似。进一步对平均周期分析， 图13给出了在各模态平均周期与分解模态阶数m在取底为2的对数， 的坐标系下的关系， 从图13中可以看到， 各模态平均周期拟合为一条斜率为1直线， 这表明CEEMD方法在湍流分解中类似于一个二分滤波器， 能够将频率相差约2倍的IMF分离出来， 这在很多研究中都有发现（Wu and Huang， 2009； Wang et al， 2013）。
表3 不同稳定条件下三个高度各IMF平均周期

Table 3 Mean period of each IMF at three altitudes under different stable conditions

IMF编号 稳定层结下平均周期/s 不稳定层结下平均周期/s
20 m 38 m 56 m 20 m 38 m 56 m
1 0.295 0.284 0.293 0.297 0.296 0.297
2 0.701 0.661 0.686 0.713 0.704 0.701
3 1.58 1.45 1.524 1.651 1.544 1.567
4 3.482 3.333 3.285 3.742 3.607 3.543
5 8.612 7.692 7.513 8.955 8.411 8.451
6 18.750 17.822 17.143 22.785 21.176 20
7 46.154 42.857 37.5 51.429 51.429 56.25
8 105.882 100 105.882 150 138.462 138.462
9 225 300 225 360 300 360
10 600 450 900 900 900 900
11 1800 1800 1800 1800 900 900
12 1800 1800 1800 1800 1800 1800
13 1800 1800 1800 1800 1800 1800
图12 平均周期随模态数m的变化

Fig.12 Variation of mean period with mode number m

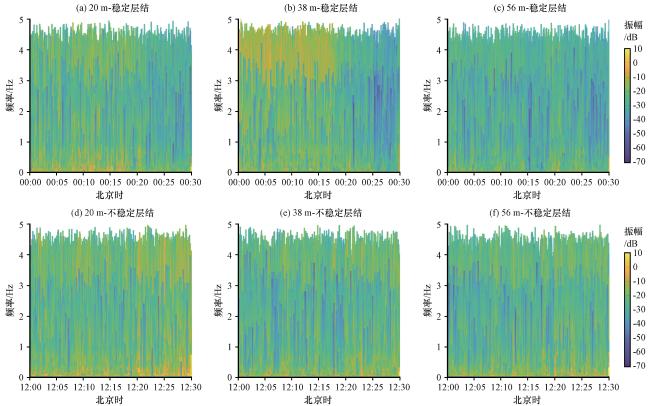
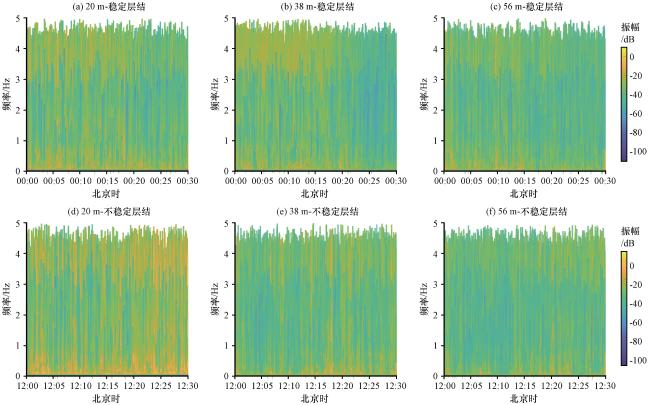
图13 夜晚和正午时刻， 稳定条件下20 m （a）、 38 m （b）、 56 m （c）和不稳定条件下20 m （d）、 38 m （e）、 56 m （f） u风三维希尔伯特谱

Fig.13 At night and noon， under stable conditions， the three-dimensional Hilbert spectra of u-winds at 20-metre （a）， 38-metre （b）， 56-metre （c）， and 20-metre （d）， 38-metre （e）， 56-metre （f） under unstable condition

对风速 u和温度 T的各模态函数做希尔伯特变换， 得到各高度的三维希尔伯特谱分别如图13和14所示， 为方便起见， 振幅单位以分贝（dB）表示。对于风速 u（图13）稳定条件下［图13（a）~（c）］， 从时间轴看在20 m［图13（a）］和38 m［图13（b）］在00:00 -00:15希尔伯特谱幅值比56 m大， 且主要集中在3.5~4.5Hz的高频段。不稳定条件下［图13（d）~（f）］， 不同高度的希尔伯特谱幅值分布相对来说比稳定条件下分布更为均匀， 差距不大。对于温度 T（图14）， 不稳定条件下［图14（d）~（f）］的三维希尔伯特谱振幅在20 m［图14（d）］处整体要比38 m［图14（e）］和56 m［图14（f））要高。如上述分析， 由于三维希尔伯特谱的信息是由原始湍流信号分解所得的IMF做变换得到， 从而保留了原始信号的某些特征， 希尔伯特谱的能量分布与上文分析的各尺度的IMF振幅分布表现一致： IMF振幅较大从而对应频率下的希尔伯特谱幅值也较高， 利用三维希尔伯特谱能够很好的分析湍流信号的时间-频率-能量的变化关系。
图14 夜晚和正午时刻， 稳定条件下20 m （a）、 38 m （b）、 56 m （c）和不稳定条件下20 m （d）、 38 m （e）、 5 6 m （f）温度 T三维希尔伯特谱

Fig.14 At night and noon， three-dimensional Hilbert spectra of temperature T at 20-metre （a）， 38-metre （b）， 56-metre （c） under stable conditions and 20-metre （d）， 38-metre （e）， 56-metre （f） under unstable conditions

为进一步分析各高度的湍流频率成分， 将三维希尔伯特谱沿着时间轴积分可以得到希尔伯特边际谱。
图15给出了不同稳定度条件下上述三个高度的三维风速 u , v , w和温度 T的希尔伯特边际谱。整体来看， 各边际谱表现形式类似， 都表现出了能量从低频到高频逐渐减小， 说明能量主要集中在大尺度湍涡上。不同稳定度条件下对比， 不稳定条件下的边际谱幅值要略高于稳定条件下的边际谱幅值， 说明不稳定条件下湍涡能量较大， 各尺度湍涡都发展得更为充分。另外， 对于三维风速 u , v , w， 相比于稳定层结， 不稳定层结下不同高度的边际谱幅值差距较小， 这可能是因为在不稳定条件下对流作用较强， 不同高度上各尺度湍涡发展交换更为充分， 特别是对于38 m和56 m处的边际谱各频段几乎重合。然而， 对于标量温度 T表现有所不同： 在稳定层结下， 各层热力交换较弱， 不同高度边际谱幅值差距反而较小， 而不稳定层结下由于太阳辐射的热力作用， 靠近下垫面的较低高度的热力吸收更强， 各高度边际谱幅值差距增大， 20 m高度处边际谱幅值明显大于其他两个高度， 并随着高度的升高而逐渐降低， 进一步说明此时热力湍涡在较低高度的发展更为充分。在不稳定条件下， 在20 m处的三维风速 u , v , w， 边际谱幅值都表现为低频段较其他高度小， 而高频段较其他高度较大的特征， 特别是对于垂直风速 w来讲， 这种低频较小的特征更为明显。这可能是因为此时对流作用较强， 同时因为观测高度较低， 离植被冠层更近， 冠层对大尺度的湍涡破碎作用更强， 导致该高度处低频大尺度湍涡较少， 以小尺度湍涡为主， 这种冠层破碎作用在一些研究中都有所发现（刘和平等， 1997； 刘树华等， 1998， 2005； 李敏和蒋维楣， 2013； 陈杰， 2014）。
图15 不同稳定度条件下各高度 u , v , w , T的边际谱

Fig.15 Marginal spectra of u， v， w， T at different heights under different stability conditions

4 结论

利用四川省乐山市四峨山人工森林地区不同高度的湍流观测数据， 介绍了希尔伯特黄变换算法， 并在传统的EMD算法的基础上引入CEEMD算法和镜像延拓算法对传统的希尔伯特黄变换算法进行了改进， 首先对比分析了传统的希尔伯特黄变换算法和改进算法的差别， 随后选取了不同稳定度条件下的个例数据应用改进算法对湍流进行分析得出了以下结论：
（1） 传统的EMD分解方法存在模态混叠现象和端点效应两种缺陷， 本文利用EMD的改进算法CEEMD解决模态混叠现象， 利用镜像延拓法解决端点效应， 并进行验证， 实验表明， CEEMD算法对于边界层湍流分解能够很好的压制模态混叠现象， 分解结果更加精细。相应的各IMF表现为模态混叠现象减小， 三维希尔伯特谱频率轴能量分布更加清晰， 边际谱存在更多的尖峰， 更好的表现了捕捉到了湍涡的能量分布特征， 便于确定各模态函数的含能情况及其湍涡尺度。
（2） 湍流信号经CEEMD分解后的模态函数中存在着4~6 min的波动周期， 这对应着3~6 min的阵风这与魏伟和张宏升（2013）对边界层湍流的研究结果是一致的。从各模态的波动周期的变化来看， 还可以发现CEEMD是一个很好的二分滤波器， 总是将周期差距大约2倍的模态函数分离出来。
（3） 本文选取了2021年5月16日一天内从夜晚稳定条件到正午时不稳定度条件下的个例数据， 结合CEEMD算法对边界层湍流进行分析， 对于风速 u和温度 T进行了个例分析， 探讨了该方法的应用。文中的个例分析中发现， u和 T的表现先在不同高度和不同层结下有所不同。对于三维风速 u , v , w不同稳定度条件下希尔伯特边际谱 表现差异较大， 不稳定条件比稳定条件下希尔伯特边际谱幅值大， 各尺度湍涡含能更高， 且不同高度不同尺度的湍涡混合较好， 另外文中的个例分析中还发现了较低高度处植被冠层对湍涡存在一定的破碎作用， 这种破碎作用在很多冠层的研究中都有发现。而对于温度 T， 稳定条件下可能近似于等温层结， 不同高度边际谱幅值差距较小， 而不稳定条件下较低高度边际谱幅值更高， 热力交换更强， 随着高度的升高边际谱幅值逐渐降低。表现了热力作用对于不同高度的不同影响。
本研究表明， HHT方法作为一个非平稳、 自适应的算法能够很好的处理大气湍流数据并能应用该方法对湍流中各尺度的湍涡进行分析， 避免了传统傅里叶变换对湍流分析的缺陷， 本文又通过结合CEEMD算法和镜像延拓法改进了传统HHT算法的缺陷， 并应用其进行分解， 发现其分解效果更好。但是也存在有一些不足。如EMD或者CEEMD算法中较为重要的一步是包络线的拟合算法， 本文基于的原始的三次样条插值算法， 该算法对于湍流这种变化剧烈的信号拟合较差， 容易产生较大误差， 若要得到更精确的模态函数需要引入更好的插值算法。

References

Publishing order | Descend order by publishing year | Descend order by cited within
Barthlott C， Drobinski P， Fesquet C， et al， 2007.Long-term study of coherent structures in the atmospheric surface layer［J］.Boundary-Layer Meteorology， 125（1）： 1-24.DOI： 10.1007/s10546-007-9190-9 .

Cava D， Katul G G， 2008.Spectral short-circuiting and wake production within the canopy trunk space of an alpine hardwood forest［J］.Boundary-Layer Meteorology， 126（3）： 415-431.DOI： 10.1007/s10546-007-9246-x .

Chen J， Heincke B， Jegen M， et al， 2012.Using empirical mode decomposition to process marine magnetotelluric data［J］.Geophysical Journal International， 190（1）： 293-309.DOI： 10.1111/j. 1365-246X.2012.05470.x .

Colominas M A， Schlotthauer G， Torres M E， 2014.Improved complete ensemble EMD： A suitable tool for biomedical signal processing［J］.Biomedical Signal Processing and Control， 14： 19-29.DOI： 10.1016/j.bspc.2014.06.009 .

Gabor D， 1946.Theory of communication： Part 1： The analysis of information［J］.Institution of Electrical Engineers-Part Ⅲ： Radio and Communication Engineering， 93（26）： 429-457.

Gao Z， Liu H， Katul G G， et al， 2017.Non-closure of the surface energy balance explained by phase difference between vertical velocity and scalars of large atmospheric eddies［J］.Environmental Research Letters， 12（3）： 34025.DOI： 10.1088/1748-9326/aa625b .

Haugen D A， Kaimal J C， Bradley E F， 1971.An experimental study of Reynolds stress and heat flux in the atmospheric surface layer［J］.Quarterly Journal of the Royal Meteorological Society， 97（412）： 168-180.

Huang N E， Shen Z， Long S R， et al， 1998.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis［J］.Proceedings of the Royal Society of London.Series A： Mathematical， Physical and Engineering Sciences， 454（1971）： 903-995.DOI： 10.1098/rspa.1998. 0193 .

Huang T L， Wei X R， Lou M L， 2008.The orthogonal Hilbert-Huang Transform and its application in earthquake motion recordings analysis［C］.Proceedings of the 14th World Conference on Earthquake Engineering， 12-17.

Huang Y， Schmitt F G， Lu Z， et al， 2007.Empirical mode decomposition analysis of experimental homogeneous turbulence time series［C］.Colloque GRETSI， 11-14.

Kaimal J C， Wyngaard J C， Izumi Y， et al， 1972.Spectral characteristics of surface-layer turbulence［J］.Quarterly Journal of the Royal Meteorological Society， 98（417）： 563-589.DOI： https： //doi.org/10.1002/qj.49709841707 .

Kolmogorov A N， 1968.The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers［J］.Proceedings of the Royal Society of London， 434（1980）： 9-13.

Lu C， Fitzjarrald D R， 1994.Seasonal and diurnal variations of coherent structures over a deciduous forest［J］.Boundary-Layer Meteorology， 69（1）： 43-69.DOI： 10.1007/BF00713294 .

Martins L G N， Miller S D， Acevedo O C， 2017.Using empirical mode decomposition to filter out non-turbulent contributions to air-sea fluxes［J］.Boundary-Layer Meteorology， 163（1）： 123-141.DOI： 10.1007/s10546-016-0215-0 .

Mauder M， Foken T， Cuxart J， 2020.Surface-energy-balance closure over land： a review［J］.Boundary-Layer Meteorology， 177（2/3）： 395-426.DOI： 10.1007/s10546-020-00529-6 .

Steiner J F， Litt M， Stigter E E， et al， 2018.The importance of turbulent fluxes in the surface energy balance of a debris-covered glacier in the Himalayas［J］.Frontiers in Earth Science （Lausanne）， 6： 00144.DOI： 10.3389/feart.2018.00144 .

Thomas C， Foken T， 2005.Detection of long-term coherent exchange over spruce forest using wavelet analysis［J］.Theoretical and Applied Climatology， 80（2/4）： 91-104.DOI： 10.1007/s00704-004-0093-0 .

Vincent C， Giebel G， Pinson P， et al， 2010.Resolving nonstationary spectral information in wind speed time series using the Hilbert-Huang transform［J］.Journal of Applied Meteorology and Climatology， 49（2）： 253-267.DOI： 10.1175/2009JAMC2058.1 .

Wang J， Song J， Huang Y， et al， 2013.Application of the Hilbert-Huang transform to the estimation of air-sea turbulent fluxes［J］.Boundary-Layer Meteorology， 147（3）： 553-568.DOI： 10. 1007/s10546-012-9784-8 .

Wei W， Zhang H， Wu B， et al， 2018.Intermittent turbulence contributes to vertical dispersion of PM in the North China Plain： cases from Tianjin［J］.Atmospheric Chemistry and Physics， 18（17）： 12953-12967.DOI： 10.5194/acp-18-12953-2018 .

Wu Z， Huang N E， 2004.A study of the characteristics of white noise using the empirical mode decomposition method［J］.Proceedings： Mathematical， Physical and Engineering Sciences， 460（2046）： 1597-1611.

Wu Z， Huang N E， 2009.Ensemble empirical mode decomposition： a noise-assisted data analysis method［J］.Advances in Adaptive Data Analysis， 1（1）： 1-41.

Yeh J， Shieh J， Huang N E， 2011.Complementary ensemble empirical mode decomposition： a novel noise enhanced data analysis method［J］.Advances in Adaptive Data Analysis， 2（2）： 135-156.DOI： 10.1142/S1793536910000422 .

Zhang Y， Liu H， Foken T， et al， 2010.Turbulence spectra and cospectra under the influence of large eddies in the Energy Balance Experiment （EBEX）［J］.Boundary-Layer Meteorology， 136（2）： 235-251.DOI： 10.1007/s10546-010-9504-1

Zhang Y， Liu H， Foken T， et al， 2011.Coherent structures and flux contribution over an inhomogeneously irrigated cotton field［J］.Theoretical and Applied Climatology， 103（1/2）： 119-131.DOI： 10.1007/s00704-010-0287-6 .

Zhu L， Qiu X， Luo J， et al， 2016.Scale properties of turbulent transport and coherent structure in stably stratified flows［J］.Applied Mathematics and Mechanics， 37（4）： 443-458.DOI： 10.1007/s10483-016-2043-9 .

白士伟， 孙刚， 李学彬， 等， 2018.小波分析在近地面湍流相干结构研究中的应用［J］.光学学报， 38（5）： 8-16.DOI： 10.3788/AOS201838.0501002.Bai S W ，

Sun G， Li X B， et al， 2018.Application of wavelet analysis in the study of coherent structure of near-surface turbulence［J］.Journal of Optics， 38（5）： 8-16.DOI： 10.3788/AOS201838.0501002 .

常娜， 李茂善， 王灵芝， 等， 2022.峨眉山地区近地层微气象特征研究［J］.高原气象， 41（1）： 226-240.DOI： 10.7522/j.issn.1000-0534.2021.00111.Chang N ，

Li M S， Wang L Z， et al， 2022.Near-surface micrometeorological characterization of the Emeishan area［J］.Plateau Meteorology， 41（1）： 226-240.DOI： 10.7522/j.issn.1000-0534.2021.00111 .

陈杰， 2014.长白山森林下垫面湍流谱特征研究［J］.现代农业科技， 42（13）： 267-270.

Chen J， 2014.Characterization of turbulence spectra in the forested subsurface of Changbai Mountain［J］.Modern Agricultural Science and Technology， 42（13）： 267-270.

程雪玲， 曾庆存， 胡非， 等， 2007.大气边界层强风的阵性和相干结构［J］.气候与环境研究， 12（3）： 227-243.DOI： 10.3969/j.issn.1006-9585.2007.03.003.Cheng X L ，

Zeng Q C， Hu F， ， et al.2007.Gustiness and coherent structure of strong winds in the atmospheric boundary layer［J］.Climate and Environment Research， 12（3）： 227-243.DOI： 10.3969/j.issn.1006-9585.2007.03.003 .

范德民， 张宇， 苏有琦， 等， 2024.川南森林湍流通量质量评价及贡献区分析［J］.高原气象， 43（1）： 227-240.DOI： 10.7522/j.issn.1000-0534.2023.00027.Fan D M ，

Zhang Y， Su Y Q， et al， 2024.Evaluation of the quality of turbulent fluxes and analysis of contributing zones in the forests of south Sichuan［J］.Plateau Meteorology， 43（1）： 227-240.DOI： 10.7522/j.issn.1000-0534.2023.00027 .

姜浩， 赵中阔， 樊伟， 等， 2018.基于经验模态分解和小波分解估算海气通量涡相关计算中的截断时间尺度［J］.海洋与湖沼， 49（6）： 1138-1150.DOI： 10.11693/hyhz20180300060.Jiang H ，

Zhao Z K， Fan W， et al， 2018.Estimation of truncated time scales in vortex correlation calculations of sea gas fluxes based on empirical modal decomposition and wavelet decomposition［J］.Oceans and Lakes， 49（6）： 1138-1150.doi： 10.11693/hyhz20180300060 .

金莉莉， 李振杰， 何清， 等， 2019.塔克拉玛干沙漠北缘夏季典型晴天近地层湍流能谱特征［J］.中国沙漠， 39（6）： 1-12.DOI： 10.7522/j.issn.1000-694X.2018.00132.Jin L L ，

Li Z J， He Q， et al， 2019.Characteristics of near-surface turbulence energy spectrum at the northern edge of Taklamakan Desert on a typical clear day in summer［J］.Desert China， 39（6）： 1-12.DOI： 10.7522/j.issn.1000-694X.2018.00132 .

李敏， 蒋维楣， 2013.Hilbert方法在大气边界层湍流特征分析中的有效性［J］.气象科技， 41（1）： 153-159.DOI： 10.3969/j.issn.1671-6345.2013.01.028.Li M ，

Jiang W M， 2013.Effectiveness of the Hilbert method in the characterization of atmospheric boundary layer turbulence［J］.Meteorological Science and Technology， ， 41（1）： 153-159.DOI： 10.3969/j.issn.1671-6345.2013.01.028 .

刘和平， 刘树华， 朱廷曜， 等， 1997.森林冠层湍流结构的特征研究［J］.北京大学学报（自然科学版）， 33（2）： 246-253.DOI： 10.13209/j.0479-8023.1997.035.Liu H P ，

Liu S H， Zhu T Y， et al， 1997.Characterization of the turbulent structure of forest canopy［J］.Journal of Peking University （Natural Science Edition）， 33（2）： 246-253.DOI： 10.13209/j.0479-8023.1997.035 .

刘树华， 李洁， 刘和平， 等， 2005.在EBEX-2000实验资料中湍流谱和局地各向同性特征［J］.大气科学， 29（2）： 213-224.

Liu S H， Li J， Liu H P， et al， 2005.Turbulence spectra and local anisotropy characteristics in EBEX-2000 experimental data［J］.Atmospheric Science， 29（2）： 213-224.

刘树华， 刘和平， Mei X， 等， 1998.森林冠层上下湍流谱结构和耗散率［J］.中国科学（地球科学）， 28（5）： 469-480.

Liu S H， Liu H P， Mei X， al et， 1998.Spectral structure and dissipation rate of turbulence above and below the forest canopy［J］.Chinese Science （Earth Science）， 28（5）： 469-480.

卢志明， 黄永祥， 刘宇陆， 2006.大气湍流的Hilbert-Huang变换分析［J］.水动力学研究与进展（A辑）， 21（3）： 309-317.

Lu Z M， Huang Y X， Liu Y L， 2006.Hilbert-Huang transform analysis of atmospheric turbulence［J］.Hydrodynamics Research and Progress （Series A）， 21（3）： 309-317.

马中存， 肖全山， 2019.镜像延拓在EMD方法中的研究及应用［J］.科技视界， 8（24）： 31-32， 118.DOI： 10.19694/j.cnki.issn2095-2457.2019.24.016.Ma Z C ，

Xiao Q S， 2019.Research and application of mirror extension in EMD method［J］.Science and Technology Perspectives， 8（24）： 31-32， 118.DOI： 10.19694/j.cnki.issn2095-2457.2019.24.016

全利红， 胡非， 程雪玲， 2007.用小波系数谱方法分析湍流湿度脉动的相干结构［J］.大气科学， 31（1）： 57-63.

Quan L H， Hu F， Cheng X L， 2007.Coherent structure of turbulent humidity pulsations analyzed by wavelet coefficient spectral method［J］.Atmospheric Science， 31（1）： 57-63.

任冉， 2014.基于集合经验模态分解（EMD-EEMD）的中国夏季降水预报方法的研究［D］： 南京： 南京信息工程大学.Ren R.2014.Research on summer precipitation forecasting method in China based on ensemble empirical modal decomposition （EMD-EEMD）［D］： Nanjing： Nanjing University of Information Engineering.

司友强， 呙润华， 施鹏程， 2019.基于EMD， EEMD与CEEMD的信号时频分析技术对比研究［J］.CT理论与应用研究， 28（4）： 417-426.

Si Y Q， Guo R H， Shi P C， 2019.Comparative study of signal time-frequency analysis techniques based on EMD， EEMD and CEEMD［J］.CT Theory and Application Research， 28（4）： 417-426.

王少影， 张宇， 吕世华， 等， 2009.金塔绿洲湍流资料的质量控制研究［J］.高原气象， 28（6）： 1260-1273.

Wang S Y， Zhang Y， Lü S H， et al， 2009.Quality control study of turbulence data in the Jinta oasis［J］.Plateau Meteorology， 28（6）： 1260-1273.

王咏薇， 王雪倩， 胡楠， 等， 2013.城市地表湍流观测数据的后处理及质量控制［J］.气象科学， 33（2）： 153-159.DOI： 10.3969/2012jms.0116.Wang Y W ，

Wang X Q， Hu N， et al， 2013.Post-processing and quality control of urban surface turbulence observations［J］.Meteorological Science， 33（2）： 153-159.DOI： 10.3969/2012jms.0116 .

魏伟， 张宏升， 2013.希尔伯特-黄变换技术及在边界层湍流研究中的应用［J］.气象学报， 71（6）： 1183-1193.DOI： 10.11676/qxxb2013.096.Wei W ，

Zhang H S， 2013.Hilbert-Huang transform technique and its application in the study of boundary layer turbulence［J］.Journal of Meteorology， 71（6）： 1183-1193.DOI： 10.11676/qxxb2013.096 .

肖瑞， 杨贤昭， 刘惠康， 2018.基于改进HHT的海浪特征频率提取［J］.高技术通讯， 28（8）： 692-699.DOI： 10.3772/j.issn.1002-0470.2018.08.004.Xiao R ，

Yang X Z， Liu H K， 2018.Wave eigenfrequency extraction based on improved HHT［J］.High Technology Letters， 28（8）： 692-699.DOI： 10.3772/j.issn.1002-0470.2018.08.004 .

杨斌， 袁祺， 谭昌海， 等， 2022.青藏高原东部拉萨河下游地区大气湍流交换特征研究［J］.高原气象， 41（1）： 204-215.DOI： 10.7522/j.issn.1000-0534.2021.00086.Yang B ，

Yuan Q， Tan C H， et al， 2022.Characterization of atmospheric turbulent exchange over the lower Lhasa River in the eastern Qinghai-Tibetan Plateau［J］.Plateau Meteorology， 41（1）： 204-215.DOI： 10.7522/j.issn.1000-0534.2021.00086 .

张汉九， 孙刚， 张坤， 等， 2022.基于Hilbert-Huang变换对近海面光学湍流特性分析［J］.激光与光电子学进展， 59（12）： 30-37.DOI： 10.3788/LOP202259.1201001.Zhang H J ，

Sun G， Zhang K， et al， 2022.Characterization of optical turbulence at near sea surface based on Hilbert-Huang transform［J］.Advances in Lasers and Optoelectronics， 59（12）： 30-37.DOI： 10.3788/LOP202259.1201001 .

张强， 文军， 武月月， 等， 2022.雅鲁藏布大峡谷地区近地面-大气间水热交换特征分析［J］.高原气象， 41（1）： 153-166.DOI： 10.7522/j.issn.1000-0534.2021.00113.Zhang Q ，

Wen J， WuY Y， et al， 2022.Characterization of near-surface-atmosphere water-heat exchange in the Yarlung Tsangpo Grand Canyon region［J］.Plateau Meteorology， 41（1）： 153-166.DOI： 10.7522/j.issn.1000-0534.2021.00113 .

Options
Outlines

/

〈 〉

The system is designed and developed by Beijing magtec Technology Development Co., Ltd. with technical support: support@magtech.com.cn