1 引言
在数值预报模式不断更新和预报技术不断发展的背景下， 社会公众对天气预报的精准度和准确性要求不断提高。因此， 对数值预报模式的诊断和改进逐渐成为气象科研工作的重要方向之一（Delle et al， 2011； Cui et al， 2012； 闫之辉等， 2010； 代刊等， 2018； 曾晓青等， 2019； 张玉涛等， 2020； 陈笑晨等， 2022； 李涛等， 2022； 欧阳鸿翔等， 2022）。2 m气温作为天气预报中最基本的要素， 在时间和空间分辨率上进行精细化既满足了社会公众对生产、 生活舒适度、 健康的要求， 也给模式检验和订正的能力提出了新的挑战（Stahl et al， 2006）。然而模式输出结果受多种因素影响， 存在一定的偏差。例如， 有学者研究发现不完善的初始和边界条件导致模式对气象要素的预报产生偏差（丑纪范， 2007； 官元红等， 2014； 徐道生等， 2014； 孙敏等， 2018）； 其次， 较大的高度偏差会严重影响模式对2 m气温的预报性能， 而且随着实际地形高度增加， 模式高度偏差和2 m气温预报偏差均呈增大趋势（智协飞等， 2019； 吴诗梅等， 2024； Pelosi， 2023）。针对温度变量， 苏海晶等（2015）研究了近30年中国夏季观测温度和模式预报温度的变化趋势， 发现模式对全球变暖存在明显的模拟不足， 导致预报误差呈上升趋势。因此， 气温预报误差在模式优化中承担重要角色（Prigent et al， 2016； Yu et al， 2019； Yu et al， 2022）。
为有效提升模式预报气温的性能， 众多学者开展了大量的误差订正和插值技术研究， 衍生出的方法包括滑动法、 递减平均法、 卡尔曼滤波、 三维空间插值、 反距离权重等数理方法和支持向量机、 随机森林、 高斯回归等机器学习方法（贺倩等， 2022）。机器学习方法是利用大量数据， 通过特征选择并训练模型， 得到输入与输出数据的映射规律进行预报（Appelhans et al， 2015； Han et al， 2021； Senior et al， 2013； 熊敏诠等， 2017； 陈昱文等， 2020； 谭晓晴等， 2022）。数理方法相比机器学习方法所需数据量更小， 业务应用更加简单广泛。早期， George and Manolis（2002）认为模式预报误差可以看作系统误差和随机误差的组成， 针对系统误差的一维卡尔曼法订正可有效提高地表温度预报准确率。基于上述理论， 马旭林等（2008）集合卡尔曼变换（ETKF）理论， 研究发展出针对中国GRAPES全球预报系统的集合初始扰动方案， 证明该方案能较好地反映分析误差方差的主要模态结构和扰动振幅， 具备合理集合离散度， 在短期预报时效内有良好的预报效果和应用前景。模式对形势场预报存在“冷偏差”， 模式本身也不可避免会产生系统性误差， 李莉等（2011）采用卡尔曼滤波的自适应误差订正方法对T213全球集合预报的一阶偏差进行订正， 改进效果显著。事实上， 依赖卡尔曼法等数理方法对误差的平滑能力， 国内外的气象学者对气温误差不断进行订正研究， 为气温精细化预报的发展提供重要的技术支撑（Isaksen et al， 2012； 贾丽红等， 2018； 郝翠等， 2019； 薛谌彬等， 2019； 王丹等， 2019； 金巍等， 2020； 李天江等， 2023）。
由于气温预报产品的订正能力在不同季节表现出差异， 学者们针对不同季节的背景场要素特征也进行了诸多研究， 如金巍等（2020）研究了固定误差订正法和最优滑动周期订正法对ECMWF模式的订正效果， 发现冬季最高气温和夏季最低气温的预报订正效果优于其他季节， 若冬季降水出现时， 最高气温预报订正效果尤其显著。基于不同模式， 贾丽红等（2018）采用递减平均法、 集合平均和加权集合平均法设计两种订正方案并订正， 发现冬季订正效果大于其他季节。依赖700 hPa层的关键区低频波信息可以部分预测未来的降温过程， 陈伯民等（2023）结合数值模式， 改善了上海地区冬季延伸期强降温预测效果。对于数值模式而言， 陈新梅等（2010）指出地形偏差的影响不容忽视， 倪悦等（2024）研究表明CMA-TRAMS模式地形偏差与模式气温预报误差线性相关， 事实上该现象也适用于大部分模式。部分学者利用温度垂直递减率（一种线性订正）订正模式地形偏差引起的气温预报误差， 取得了正订正效果（王思维等， 2011； 王田野等， 2016； 夏凡等， 2018）。
常规的模式时间分辨率很难准确描述气温的周期性特征（Jhajharia and Singh， 2011）， 而国内研究主要集中在ECMWF等主流预报模式的误差订正方法， 重点探讨最高和最低气温的订正效果（吴启树等， 2016； 潘留杰等， 2017； 王丹等， 2019； 薛谌彬等， 2019； 冯良敏等， 2023）。相比之下， 对于国产和逐小时气温预报的订正研究相对较少。CMA-GD是华南区域中尺度数值模式（China Meteorological Administration Guangdong）的简称， 国内相关研究包括对CMA-GD模式逐时降水预报性能的分区评估（Feng et al， 2023）、 对模式预报风速性能的检验（Xu et al， 2023）、 以及利用最优TS评分订正法（OTS）对模式逐小时降水量进行订正的研究（刘段灵和陈超， 2022）等。本文结合对地形高度偏差导致的气温误差订正法（倪悦等， 2024）和数理订正方法的再订正， 包括一维卡尔曼滤波法（George and Manolis， 2002）和滑动双权重平均法（薛谌彬等， 2019）， 对CMA-GD模式逐小时气温预报产品进行订正和检验， 旨在完善本地适用的复合订正方法。本研究结果将系统评估复合方法的订正性能， 有助于减少模式气温预报偏差和提高预报准确率， 为精细化网格预报的发展提供参考。
2 资料来源和方法介绍
2.1 资料来源
站点实况资料： 选取江西智能网格预报区域（113.43°E -118.6°E， 24.34°N -30.2°N）168个气象站的海拔资料作为实际高度； 选取2021年3月1日至2022年3月1日的逐小时2 m气温观测资料用于建立地形订正的回归； 2022年3月1日至2023年3月1日的逐时观测资料被用于检验地形订正效果和数理方法的再订正。站点及预报区域海拔分布情况如图1所示。同时， 为评估方法在不同地形区的订正效果， 选取鄱阳湖平原中部（115.5°E -117°E， 28.5°N -29.5°N， 见图1蓝色方框）、 浙闽丘陵南部（116.5°E -118.6°E， 25°N -27°N， 见图1红色方框）两个地形区和黄山（图1蓝点）、 庐山（图1黑点）、 九仙山（图1绿点）三个高海拔山区作为研究对象。文中所涉及的地图均基于中华人民共和国自然资源部地图技术审查中心标准地图服务系统下载的审图号为GS（2017）3320号的中国地图制作， 底图无修改， 文中所用时间为北京时。
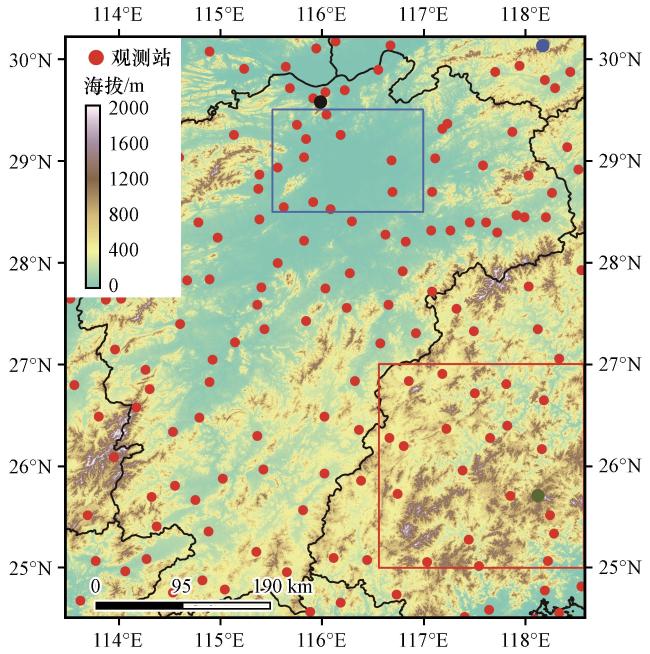
图1 江西智能网格预报区域观测站和海拔分布 蓝色方框标注鄱阳湖平原中部， 红色方框标注浙闽丘陵南部， 蓝色点标注黄山， 黑色点标注庐山， 绿色点标注九仙山Fig.1 The distribution of the observation station and the elevation in Jiangxi intelligent grid forecast domain.The blue box on the map indicate the the middle part of Poyang Lake Plain， the red box indicate the south Zhejiang-Fujian hilly region， the blue dot indicate Huangshan， the black dot indicate Lushan， the green dot indicate Jiuxianshan |
模式输出资料： 选取CMA-GD模式的高度资料， 提取预报区域168个气象站的高度数据用于计算模式高度偏差； 选取CMA-GD模式输出的2021年3月1日至2022年3月1日2 m气温逐时预报资料用于建立地形订正的回归； 选取2022年3月1日至2023年3月1日的逐时预报资料用于检验地形订正效果和数理方法的再订正。CMA-GD模式每日两次提供具有网格要素特征的产品（预报起始时间为08:00和20:00）， 空间分辨率为0.03°×0.03°。由于模式的滞后性， 12 h内的资料预报员无法参考， 且早上的产品足以覆盖所有预报时效， 综合实际预报业务需求， 本文选择08:00起报产品， 预报时效为13~36 h。
插值方法： 空间插值基于“地理学第一定律”的假设， 即空间位置上越靠近的点， 具有相似特征值的可能性越大（Benavides et al， 2007）。性能卓越且应用广泛的插值法包括反距离权重插值法、 样条函数插值法、 泰森多边形法和克里金插值法等（李海涛和邵泽东， 2019）。部分研究区域地形复杂， 温度对垂直高度变化敏感， 学者们采用温度垂直递减率插值法进行订正， 并有效减少地形差异导致的误差（赵滨和张博， 2018）。杨富燕等（2023）针对贵州地形复杂的特点， 对中国气象局陆面数据同化系统（CLDAS）温度产品使用考虑地形的双线性插值法， 发现超80%的站点插值高度与实际高度差异不超过±200 m。为了尽可能地减小地形对气温的影响， 本文同样采用双线性插值法， 将网格要素插值到站点。
2.2 方法介绍
2.2.1 地形高度偏差导致的气温误差订正方法
采用地形高度偏差和2 m气温预报误差建立的一元线性订正方法， 具体公式如下：
式中： 表示i站点模式高度偏差； 表示i站点2 m气温预报误差； a、 b均为系数； 表示i站点在t时刻的2 m气温预报值； 表示订正后的2 m气温预报值。
根据模式地形偏差和2021年3月1日至2022年3月1日的2 m气温预报误差平均值的分布特点， 建立三种订正回归关系： 不分级回归关系、 地形高度偏差分级回归关系（划分为小于-50 m、 -50~50 m之间和大于50 m）、 2 m气温预报误差分级回归关系（划分为小于-2 ℃、 -2~2 ℃之间和大于2 ℃）， 对比三种订正回归关系并择优使用。
2.2.2 数理订正方法
一维卡尔曼滤波法： 卡尔曼滤波法通过计算前一时效的预报误差， 修正预测方程， 预测订正时刻的误差， 对模式预报结果进行订正（马旭林等， 2015）。本文采用卡尔曼滤波法并简化成一维， 具体公式组成如下：
系统误差公式：
观测误差公式：
预测公式：
更新公式：
计算订正结果：
式中： 代表系统误差； 代表随机误差， 即模式误差与系统误差的差值； 代表预报模式误差； 代表协方差矩阵； 代表卡尔曼增益； 代表订正后预报值； 代表订正前预报值； 初始 、 =0， 、 =4。
George and Manolis （2002）认为适用于NWP模式的计算方法应分别采用协方差矩阵 和 的七天样本方差（n=7）， 其中 ， ， 但未说明第一个订正时次前七天协方差矩阵的计算方法， n=7也不一定是CMA-GD模式的最优解。本文结合业务实践， 设N=｛5， 7， 10， 15， 20， 25， 30， 40， 50｝， n∈N， 进行多次实验。第一个订正时次前n天固定 =0， =4。
滑动双权重平均法： 滑动双权重平均法是本文第二种订正方法， 具体公式如下：
=
式中： 代表第k个测站在n时次订正后的温度； 代表当前站点模式预报温度； 代表订正项； 代表周期n内的 的中位数。通过实验发现， 中位数可减弱异常值对整体趋势的影响， 平均值可反映一组数据的整体水平。本文未针对最高、 最低气温进行订正， 使用平均值法可能优于中位数法。因此分别对采用平均值和中位数的双权重滑动平均法进行同周期检验对比， 并设N=｛5， 10， 15， 20， 25， 30， 40， 50｝， n∈N。
是 的中位数或平均值。若 ， 取 ； 若 ， 取 。
2.2.3 再订正实验方案
本文中设计了如下实验方案： （1）使用一维卡尔曼滤波法， 订正周期为7 d， 作为对照实验； （2）使用一维卡尔曼滤波法， 订正周期分别为5、 10、 15、 20、 25、 30、 40、 50 d， 寻找最优订正周期； （3）使用滑动双权重平均法， 和 均采用中位数， 订正周期分别为5、 10、 15、 20、 25、 30、 40、 50 d， 寻找最优订正周期并作为对照实验； （4）使用滑动双权重平均法， 和 均采用平均值， 订正周期分别为5、 10、 15、 20、 25、 30、 40、 50 d， 寻找最优订正周期； （5）对比中位数法和平均值法的订正效果并择优使用。
2.2.4 误差分析方法
选取平均绝对误差（Mean Absolute Error）和预报准确率（Accuracy）来定量检验模式的气温预报性能和方法订正效果， 计算公式如下：
式中： 代表模式预报气温； 代表实况气温； 为预报误差绝对值≤2 ℃的站数； 为总站数。
3 地形偏差导致的气温误差订正结果分析
对模式地形高度偏差和2021年3月1日至2022年3月1日的2 m气温预报误差平均值进行线性回归（图2）， 分析后发现占比超过95%的气温预报误差平均值位于-2~2 ℃， 如果对误差分级， 则组间数据量差异过大， 因此本文中不适用气温误差分级回归。不分级回归结果表明［图2（a）］， 模式地形高度偏差与2 m气温预报误差平均值呈负相关关系， 检验p值为4.1335× ， 通过显著性检验； 高度偏差分级后建立了三个回归方程 、 、 ［图2（b）］， =0.0024小于0.05通过显著性检验， =0.4833、 =0.2075未通过显著性检验， 因此不适用高度偏差分级回归。综上所述， 本文使用不分级回归方法对模式地形偏差导致的气温误差进行订正（简称不分级回归法）。对2022年3月1日至2023年3月1日的2 m气温预报产品订正后发现（表1）， 白天时段的MAE降低0.14 ℃， ACC提高3.3%； 夜间时段的MAE降低0.05 ℃， ACC提高1.9%， 白天的订正幅度大于夜间。准确率逐时效分布表明（图3）， 不分级回归方法总体为正订正， 23 h、 24 h、 25 h为负订正， 35 h的订正效果最好， 订正后准确率提高4.7%， 24 h的订正效果最差， 订正后降低1.6%。在13~24 h预报时效内（对应夜间预报时段）ACC在70%~75%范围内先增加后减小， 准确率浮动范围不大， 在25~36 h预报时效内（对应白天预报时段）准确率先迅速降低后增加， 呈“V”型分布， 32 h达到最低（订正前为46.5%， 订正后为51.1%）。
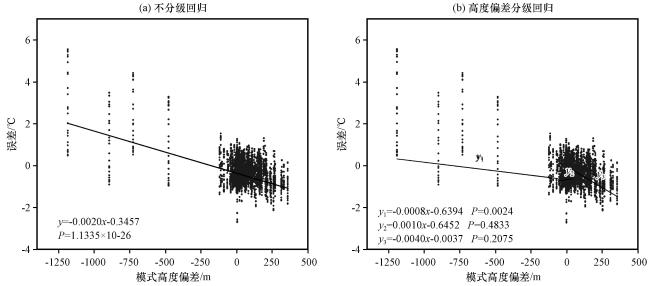
图2 2021年模式气温误差与地形高度偏差的分布及不分级回归分析（a）、 高度偏差分级回归分析（b）Fig.2 Distribution and ungraded regression analysis （a）， graded regression analysis of height error （b） of 2021 model temperature error and terrain height error |
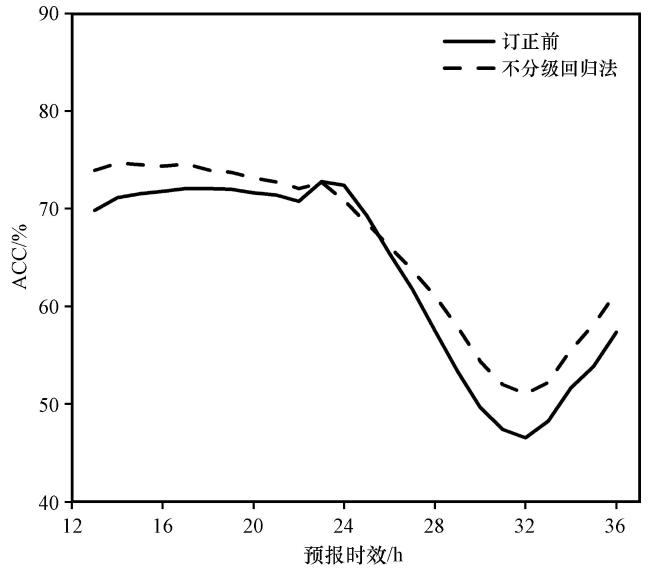
表1 2022年订正前和不分级回归法订正后平均MAE及ACCTable 1 Average MAE and ACC before and after the Correction of ungraded regression method in 2022 |
| 时段 | 订正前 | 不分级回归法 | ||
|---|---|---|---|---|
| MAE/℃ | ACC/% | MAE/℃ | ACC/% | |
| 白天 | 2.14 | 55.2 | 2.00 | 58.5 |
| 夜间 | 1.50 | 71.6 | 1.45 | 73.5 |
4 再订正结果分析
4.1 确定最优周期
将不分级回归方法和数理方法结合组成复合订正方法， 表2显示了使用不同周期一维卡尔曼滤波法订正后的年平均MAE和ACC。结果表明使用7 d周期的一维卡尔曼滤波法并不是最佳方案， 而使用15 d周期的一维卡尔曼滤波法能够使误差最小， 准确率最高。确定本文中卡尔曼法的订正周期为15 d。
表2 2022年不同周期的一维卡尔曼滤波法再订正后平均MAE及ACCTable 2 Average MAE and ACC after re-correction by one-dimensional Kalman filtering method with different periods in 2022 |
| 误差参数 | 不同周期的一维卡尔曼滤波法再订正后参数平均值 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 5 d | 7 d | 10 d | 15 d | 20 d | 25 d | 30 d | 40 d | 50 d | |
| MAE/℃ | 1.57 | 1.56 | 1.55 | 1.55 | 1.56 | 1.57 | 1.58 | 1.59 | 1.61 |
| ACC/% | 71.50 | 71.90 | 71.90 | 72.20 | 72.00 | 71.40 | 71.10 | 70.60 | 70.00 |
使用不同周期滑动双权重平均法进行订正， 分别对 和 采用中位数或平均值（表3）后发现， 两种方法各有优劣。平均值法相比中位数法在中短周期（5 d、 10 d、 15 d和20 d）下准确率更高， 误差更小， 而在长周期（25 d、 30 d、 40 d和50 d）下准确率更低， 误差更大。综合实验结果表明， 双权重滑动平均法采用周期n=20 d订正效果最。由于使用不同参数的双权重滑动平均法间订正效果较为接近， 本文仅采用周期为20 d的平均值法进行再订正。
表3 2022年不同周期的中位数法、 平均值法再订正后平均MAE及ACCTable 3 Average MAE and ACC after re-correction by median method， mean method with different periods in 2022 |
| 误差参数 | 不同周期的中位数法、 平均值法再订正后参数平均值 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 5 d | 10 d | 15 d | 20 d | 25 d | 30 d | 40 d | 50 d | ||
| 中位数法 | MAE/℃ | 1.55 | 1.53 | 1.51 | 1.50 | 1.50 | 1.50 | 1.52 | 1.55 |
| ACC/% | 72.10 | 72.70 | 73.20 | 73.60 | 73.60 | 73.40 | 72.80 | 72.00 | |
| 平均值法 | MAE/℃ | 1.54 | 1.53 | 1.51 | 1.49 | 1.50 | 1.51 | 1.52 | 1.55 |
| ACC/% | 72.50 | 72.90 | 73.40 | 73.70 | 73.60 | 73.30 | 72.70 | 71.90 | |
4.2 订正结果逐时效分布分析
在不回归分级法的订正基础上， 对2022年3月1日至2023年3月1日的气温产品采用15 d周期的卡尔曼法和20 d周期的平均值法进行复合订正， 结果如表4所示， 两种方法都表现出正向订正效果， 其中平均值法相较于卡尔曼法， 在白天时段将MAE降低了0.04 ℃， ACC提高了1.5%， 夜间时段将MAE降低0.06 ℃， ACC提高了1.7%。总体来看， 平均值法的订正幅度大于卡尔曼法。ACC逐时效分布表明（图4）， 35 h的订正效果最好（相比订正前， 卡尔曼法提升了25.7%， 平均值法提升了28.7%）。相比订正前的ACC， 平均值法在白天提升了22.5%， 夜间提升了11.0%， 白天的平均准确率提升幅度大于夜间。数理方法的再订正有效提高了准确率。
表4 卡尔曼法、 平均值法订正再后平均MAE及ACCTable 4 Average MAE and ACC after re-correction by Kalman method and mean method |
| 时段 | 卡尔曼法 | 平均值法 | ||
|---|---|---|---|---|
| MAE/℃ | ACC/% | MAE/℃ | ACC/% | |
| 白天 | 1.77 | 66.0 | 1.73 | 67.5 |
| 夜间 | 1.33 | 77.8 | 1.27 | 79.5 |
对CMA-GD模式的气温产品进行订正后， 得到不同季节的ACC逐时效分布（图5）。研究结果显示， 不分级回归法订正同数理方法再订正之间的预报准确率差值存在日变化和季节变化特征。在春季夜间， 不分级回归法的准确率相比平均值法和卡尔曼法的准确率差距不大， 春季白天， 经过数理方法再订正准确率变化不大， 卡尔曼法准确率最低， 从时效分布来看， 20 h的订正效果最差， 卡尔曼法准确率为58.6%， 平均值法为60.3%， 相比不分级回归法（63.0%）分别降低4.4%、 2.7%。这种负订正可能与数理方法输出结果的平均状态和CMA-GD模式热力框架、 初始场同化等对春季模拟的气温变化趋势不一致造成的， 具体原因尚待进一步研究。在夏、 秋、 冬季， 数理方法的再订正有效提高了准确率， 夏季平均值法准确率最高， 卡尔曼法次之， 36 h的订正效果最好， 卡尔曼法和平均值法分别提高12.4%、 17.7%； 秋季白天订正效果优于夜间， 卡尔曼法、 平均值法准确率差距不大， 34 h订正效果最好， 卡尔曼法、 平均值法分别提高30.4%、 31.4%； 冬季的26 h订正效果最优， 卡尔曼法和平均值法间差距不大。总体来看， 由于江西夏、 秋季冷空气过程少， 连晴天居多， 逐时气温变化趋势较规律， 导致误差容易被数理方法平滑， 因此夏、 秋季的再订正相比地形订正显著提高了准确率， 冬季次之， 而春季则表现最差。夏季夜间的订正效果优于白天， 而秋、 冬季白天的订正效果优于夜间。
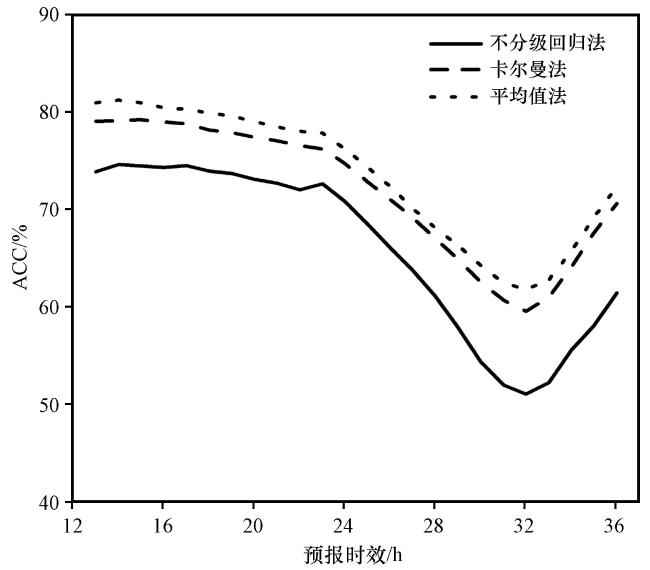
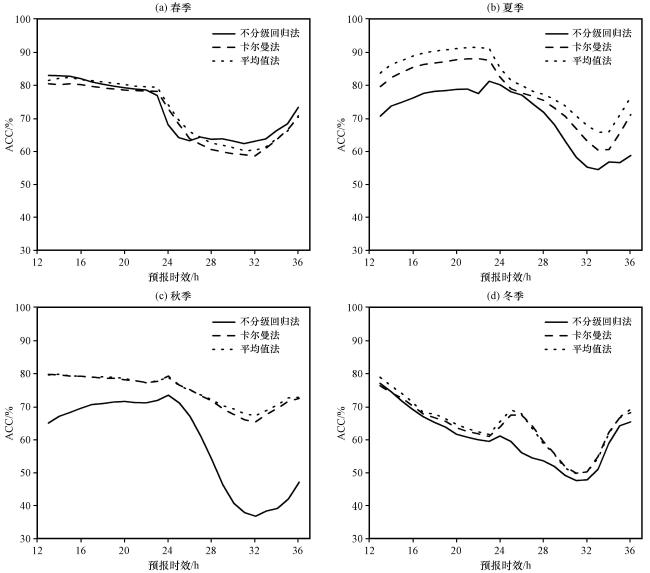
图5 卡尔曼法、 平均值法再订正后不同季节的ACC逐时效分布（以不分级回归法订正结果为参照）（a） 春季， （b） 夏季， （c） 秋季， （d）冬季Fig.5 Hourly ACC distribution after re-correction by Kalman method and mean method in different seasons （Reference to the result after correction by ungraded regression）.（a） Spring， （b） Summer， （c） Autumn， （d） Winter |
4.3 订正后空间分布特征
从气温产品订正前的站点年平均MAE及ACC空间分布（图6）可以看出， 大部分站点年平均MAE集中在1.4~2.2 ℃区间， 年平均ACC集中在55%~80%区间， 福建沿海地区误差最小， 准确率最高， 其次是环鄱阳湖区域。庐山（海拔1841.4 m）的MAE超过2.4 ℃， ACC低于50%， 黄山站（1841.4 m）海拔最高， MAE超过3.6 ℃， 九仙山站（海拔1654.6 m）也超过2.6 ℃， 两者ACC均低于40%。该现象与模式地形高度偏差和气温预报误差的负相关关系相吻合， 也就是模式对高海拔地区的模拟相比实际地形更容易偏低， 而气温误差偏高。同理海拔越低， 地形偏差越小则气温误差越小， 若模式地形相比实际地形偏高， 气温误差则倾向于负值。图7展示了不分级回归法和卡尔曼法、 平均值法相对于订正前的MAE、 ACC差值空间分布。结果表明， 不分级回归法订正后有8个站为负订正， 负订正率为4.7%， MAE差值大部分分布在0~0.2 ℃区间， 黄山（0.83 ℃）的正订正差值最大， 九仙山（0.61 ℃）次之。再订正后消除负订正站点， 卡尔曼法的差值大部分分布在0~0.6 ℃区间； 平均值法的差值大部分分布在0.2~0.6 ℃区间， 黄山（1.50 ℃）差值最大， 九仙山（1.16 ℃）次之。从ACC订正插值的分布可以看出， 卡尔曼法、 平均值法的再订正相比不分级回归法显著提升了准确率， 正订正差值大部分分布在0~6%， 黄山（18.6%）的正订正差值最大， 九仙山（11.6%）次之。再订正消除了负订正站点， 大部分差值超过了6%， 黄山为25.4%， 九仙山为31.6%。总体而言， 对包括长江中下游、 环鄱阳湖区域等预报区域北部的订正效果优于南部， 对于高山站， 地形起伏越大， 则订正前误差越大， 订正后订正效果越显著。
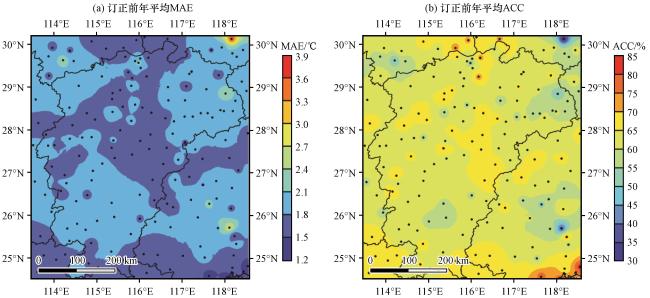
图6 订正前的年平均MAE（a）和ACC（b）空间分布Fig.6 Spatial distribution of annual average MAE （a） and ACC （b） before correction |
图7 不分级回归法订正后（左）和卡尔曼法（中）、 平均值法（右）再订正后年平均MAE（a~c）和ACC（d~f）相对于订正前的差值的空间分布Fig.7 Spatial distribution of the difference between after correction and before correction about the annual average MAE （a~c） and ACC （d~f） by the ungraded regression method （left）， re-correction by Kalman method （medium） and mean method （right） |
上述分布结果表明， 方法对预报准确率的订正效果与订正前模式的偏差大小可能存在部分相关， 为了进一步验证该相关性是否符合线性， 对所有国家站在订正前的逐时效MAE和ACC订正幅度占比（ACC订正幅度占比=ACC订正幅度/订正前ACC）进行拟合， 结果如图8所示。散点分布更接近二项式分布， 其中不分级回归法R²=0.4964， 卡尔曼法R²=0.6634， 平均值法R²=0.7858， 平均值法的相关性最好， 证明了模式订正前的MAE越大， 订正后的ACC相对提升也越大， 订正效果也更好。分析斜率发现， 平均值的斜率最大， 卡尔曼次之， 不分级回归订正后斜率最小， 这表明不分级回归法虽然在一定程度上可以消除模式地形偏差导致的预报准确率损失， 但总体订正效果有限。经数理订正方法的再订正后， 有效提升了准确率的订正幅度。
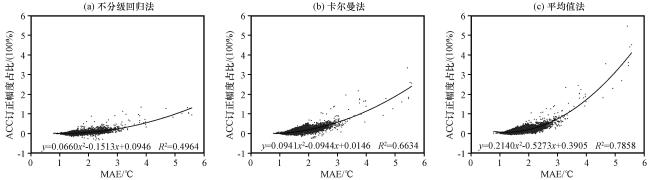
图8 所有国家站预报时效的订正前MAE和平均值法订正后ACC订正幅度占比（单位： 100×%）拟合图（a） 不分级回归法， （b） 卡尔曼法， （c） 平均值法Fig.8 Fitting diagram of MAE before correction and the proportion of ACC correction margin after the correction by mean methods for all forecast hours of national stations.（a） Ungraded regression method， （b） Kalman method， （c） Mean method |
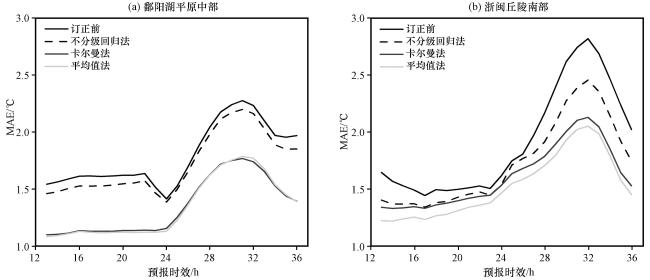
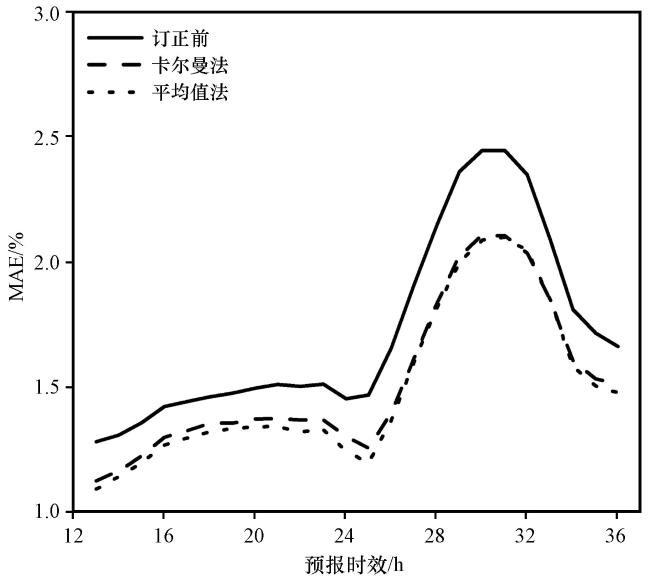
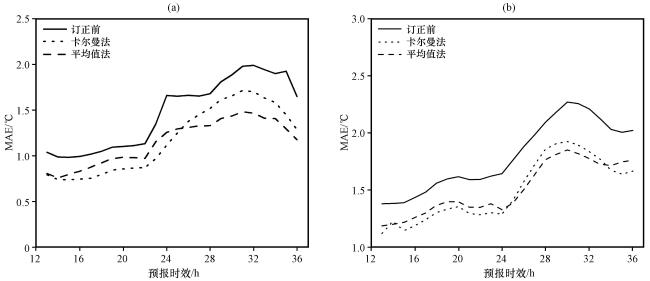
4.4 鄱阳湖平原中部和浙闽丘陵南部地区的误差订正效果检验
江西智能网格预报区域内地形分布复杂， 既包括以鄱阳湖冲湖积平原为主体的长江中下游平原部分地区， 又包括浙闽丘陵、 赣中丘陵、 武夷山脉等以丘陵、 山地为主的复杂地貌区。由于模式地形与实际存在差异， 高度偏差导致高分辨率温度产品在复杂地形下插值会产生误差（陈康凯等， 2020； 杨富燕等， 2023）， 模式与实际地形的高度差越大导致预报误差越大（智协飞等， 2019）。为研究在不同下垫面环境影响下数值模式气温预报偏差的订正效果， 以鄱阳湖平原中部和浙闽丘陵南部区域为例（见图1蓝色方框和红色方框）， 年平均MAE如图9所示。在全天时段中， 订正前两个地形区MAE普遍超过1.5 ℃， 夜间时段（13~24 h）误差变化平缓， 白天时段（25~36 h）误差迅速增加呈单峰型， 鄱阳湖平原地区误差峰值（2.27 ℃）小于浙闽丘陵地区（2.82 ℃）， 主要原因在于平原地形偏差小于丘陵地形偏差［图9（a）、 （b）虚线的分布表明进行不分级回归订正后， 图9（b）误差下降幅度显著大于图9（a）］， 鄱阳湖平原因地形偏差导致气温预报的系统性误差更小， 也导致鄱阳湖平原地形偏差的订正效果更差。
鄱阳湖是中国最大的淡水湖， 鄱阳湖平原区又是冷空气入侵江西预报区域的重要路径之一。当冷空气抵达时， 湖面风力等级远大于有地形阻挡的丘陵区。2022年11月至2023年1月共有4次寒潮入侵过程， 对该时段鄱阳湖平原中部区域的订正效果进行检验发现（图10， 只展示复合订正的结果， 地形订正略， 下同）， 订正后MAE平均降低0.23 ℃， 较订正前的平均MAE降低13.5%， 最大降幅出现在29 h， 较订正前降低17.0%。结果表明， 在多冷空气入侵、 风力较大等动力因素影响下， 复合方法对气温误差的订正依然取得了稳定的效果。
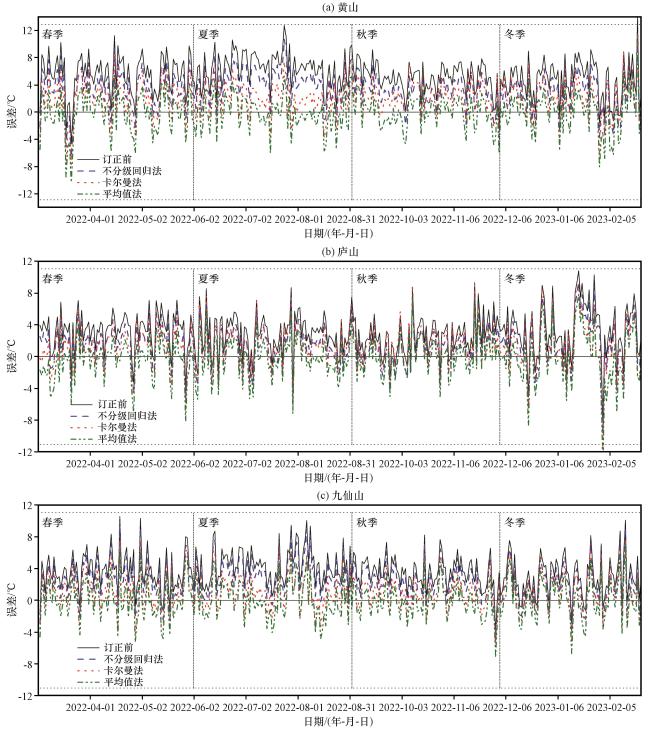
4.5 高海拔山区逐日订正效果检验
为了进一步检验客观方法对高海拔山区的订正效果， 本文选取黄山、 庐山和九仙山（见图1蓝点、 黑点、 绿点）的32 h全年逐日误差进行订正效果评估， 图11表明， 模式对高山站的气温预报显著偏高， 尤其在春、 冬两季更频繁受冷空气影响的情况下， 气温骤降几率大， 导致逐时气温预报难度加大。因此， 夏季和秋季的误差振荡幅度小于春季和冬季。同理， 在8 -10月， 降水显著减少， 连晴天气导致逐时气温变化规律， 误差振荡幅度最小。不分级回归法的订正削弱了模式地形偏差导致的气温预报误差， 经过卡尔曼法、 平均值法的再订正， 预报误差在0轴附近振荡， 大部分可控制在±4 ℃区间， 部分时段可控制在±2 ℃以内， 夏、 秋季相比春、 冬季订正后误差更小。研究结果证明该复合订正方法可有效减小高海拔山区的系统性正误差。需要强调的是， 本方法对改善模式预报误差的离散程度效果有限， 因此存在部分结果的“过订正”现象， 即误差正值订正后变为负值， 这也是一维数理订正方法的局限性， 今后可以针对二维方法做进一步研究。
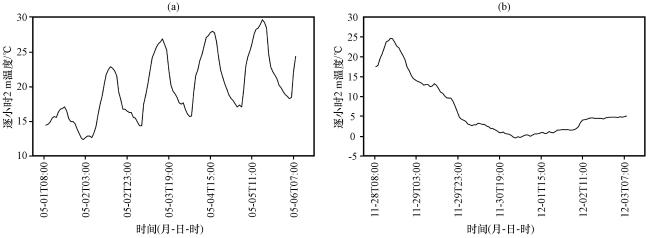
4.6 转折性天气订正效果检验
从上述检验可以看出， 由不分级回归法和卡尔曼法、 平均值法组成的复合订正方法不仅对整体区域取得了正订正结果， 对特殊地形区和高海拔山区也取得了稳定的正订正效果。为了进一步评估客观方法对转折天气过程的预报性能， 本文以2022年5月1 -6日的显著增温过程和2022年11月28日至12月3日的寒潮降温过程为例。2022年5月1 -6日处高压脊前偏北气流中， 研究区域阴转晴迎来持续增温， 以南昌逐时气温为例［图12（a）］， 其中5月1 -2日最高气温增温最大为5.8 ℃， 2 -3日次之为4.0 ℃。经方法订正后［图13（a）］， MAE的平均降幅为18.2%， 订正前最大值出现在32 h， 最大值为1.99 ℃， 平均值法订正效果最好， 订正后为1.47 ℃， MAE降幅为26.3%。2022年11月28日至12月3日受强寒潮影响， 研究区域迎来强降温、 降雨（雪）、 大风天气， 部分地区出现道路结冰。以南昌为例［图12（b）］， 11月28日15:00最高气温为24.6 ℃， 至11月30日03:00最低降至-0.4 ℃， 降温幅度为25.0 ℃， 11月30日至12月3日气温缓慢回升， 增幅为5.5 ℃。经方法订正后［图13（b）］， MAE的平均降幅为16.0%， 订正前最大值为2.27 ℃， 出现在30 h， 平均值法订正效果最好， 订正后为1.85 ℃， MAE降幅为18.4%。总体而言， 本文客观方法针对强降温和增温过程均有稳定的正订正能力。
图12 2022年5月1日08:00至6日08:00（a）和2022年11月28日08:00至12月3日08:00（b）的南昌逐时气温分布Fig.12 Hourly distribution of temperature for Nanchang from 08:00 on 1 to 08:00 on 6 May 2022（a） and from 08:00 28 November to 08:00 3 December 2022（b） |
5 结论
本研究利用江西智能网格预报区域的168个国家观测站的海拔数据、 CMA-GD模式的高度数据以及2021年3月1日至2023年3月1日的气温实况资料和CMA-GD模式的逐时气温预报产品。通过双线性插值法将格点产品插值到站点， 基于2021年的数据， 利用地形偏差和气温年均误差数据回归建立了不分级回归订正方法（不分级回归法）， 对2022年的数据进行地形订正， 同时采用一维卡尔曼滤波法（卡尔曼法）、 采用中位数和平均值参数的滑动双权重平均法（中位数法和平均值法）进行再订正。通过对订正前后的平均绝对误差（MAE）和预报准确率（ACC）进行检验， 得出以下结论：
（1） 模式地形高度偏差与预报的气温误差平均值呈线性负相关。在比较不同的地形订正方法时， 发现超过95%的数据分布在-2~2 ℃， 因此不适用温度误差分级回归法。对地形高度偏差分级回归法和不分级回归法进行显著性检验， 结果表明三个高度偏差分级方程中 通过显著性检验， 、 未通过显著性检验， 因此不适用高度偏差分级回归法； 不分级回归方程y通过显著性检验， 因此本文采用不分级回归的地形偏差订正法。2022年数据的地形订正结果显示： 白天预报时段（25~36 h预报时效内）的准确率呈现“V”型分布， 其中32 h准确率最低， 而夜间预报时段（13~24 h预报时效内）的准确率变化不大； 总体来看， 不分级回归法为正订正， 白天时段的订正效果优于夜间时段， 其中35 h的订正效果最佳， 24 h的订正效果最差。
（2） 将不分级回归法和数理方法组合为复合方法， 可以选择最优订正周期。其中卡尔曼法使用15 d周期订正后误差最小， 准确率最高， 对比7 d的原方法减小了年平均MAE， 提高了ACC。检验双权重滑动平均法， n=20 d订正效果最好， 对比中位数法和平均值法， 平均值法在中短周期（5 d、 10 d、 15 d和20 d）订正较好， 中位数法在长周期（25 d、 30 d、 40 d和50 d）订正较好。由于双权重滑动平均法采用不同参数后订正效果接近， 为了更好地展示订正效果， 本文使用n=20 d的平均值法进行分析。
（3） 使用20 d周期的平均值法进行订正比使用15 d的卡尔曼法效果更好。平均值法相较于卡尔曼法， 白天的平均绝对误差（MAE）降低了0.04 ℃， 准确率提高了1.5%， 夜间的MAE降低了0.06 ℃， 准确率提高了1.7%。对比平均MAE和ACC， 白天的订正表现优于夜间。在预报时效方面， 35 h的订正效果为最优， 23 h为最差。季节间的对比检验表明， 春季白天的订正效果最差， 夏季的订正效果最好， 平均值法的准确率最高， 卡尔曼法次之。而在秋、 冬季， 订正效果也为正订正， 但卡尔曼法和平均值法之间的差异不大， 白天的效果优于夜间。由于夏、 秋季气候特征导致逐时气温变化较规律， 数理方法对误差的平滑效果显著， 再订正效果优于冬季和春季。
（4） 大部分站点在订正前年平均MAE分布在1.4~2.2 ℃， 年平均ACC分布在55%~80%。总体趋势表明， 海拔越高， MAE值越大， ACC值越低。其中黄山为最高海拔站， MAE超过3.6 ℃， ACC均低于40%。经不分级回归法订正后， 有8个站点为负订正， 负订正率为4.7%。经卡尔曼法再订正后， 消除了MAE负订正点， 大部分正订正差值的分布由0~0.2 ℃提升到0~0.6 ℃， 平均值法则提升到0.2~0.6 ℃， 黄山正订正差值最大为1.50 ℃。ACC再订正后无负订正点， 再订正前正订正差值分布为0~6%， 再订正后大部提升6%以上， 九仙山站提升最大为31.6%。研究表明， 复合订正方法对预报区域北部的订正效果整体优于南部， 尤其对高山站的订正效果最为显著。对订正前的逐时效MAE和ACC订正幅度占比进行拟合检验后发现， 两者更接近二项式正相关分布， 其中平均值法相关性最好， 卡尔曼法次之， 不分级回归法相关性最差。斜率分布显示仅对地形偏差导致的气温误差进行订正， 准确率订正幅度有限， 而使用数理方法进行复合订正可以有效提高准确率的订正幅度。
（5） 选取鄱阳湖平原中部和浙闽丘陵南部区域为特殊地形区， 对地形区的MAE进行订正评估。订正前， MAE普遍超过1.5 ℃， 全天误差分布呈单峰型， 鄱阳湖平原中部的误差峰值小于浙闽丘陵南部。不分级回归法订正后， 结果显示方法对浙闽丘陵因地形导致的气温误差订正效果最好， 对误差峰值处的订正幅度也大于鄱阳湖平原。复合订正后， 鄱阳湖平原中部的MAE平均降幅为25.1%， 浙闽丘陵南部的MAE平均降幅为19.8%。对2022年11月至2023年1月的鄱阳湖平原中部MAE进行检验， 平均MAE降低13.5%， 29 h为17.0%， 为全时段最大降幅。在多冷空气入侵、 风力较大背景下的鄱阳湖平原中部， 复合方法依然取得了稳定的订正效果。
（6） 对黄山、 庐山和九仙山进行检验后发现， 方法对高海拔山区的正系统性误差订正效果显著。在订正前气温预报显著偏高， 夏、 秋季的误差振荡幅度小于春、 冬季， 8 -10月的气温误差振荡幅度最小。通过不分级回归法订正了部分气温误差， 经数理方法再订正后误差围绕0轴振荡， 且误差范围在±4 ℃之内。
（7） 客观方法对增温和降温过程均具有稳定的订正能力。以增温过程为例（2022年5月1 -6日）， 订正后MAE平均降低18.2%， 误差最大值出现在32 h， 该时效误差订正后降幅为26.3%； 以强降温过程为例（2022年11月28日至12月3日）， 订正后MAE平均降低16.0%， 误差最大值出现在30 h， 该时效误差订正后降幅为18.4%。
本文客观方法在数理订正方法的基础上， 引入模式地形数据， 将数理订正和地形订正相结合形成复合订正方法。然而， 文中仅考虑了模式地形数据、 实际海拔数据、 逐小时2 m气温实况数据和模式预报数据， 没有考虑风力、 湿度等其他气象要素的影响， 但经过评估， 该方法对不同地形区、 转折性天气具有稳定的订正能力， 尤其是对高海拔山区的订正效果较好， 考虑到以下几个因素： （1）将其他气象要素融入进数理订正方法， 可能要改变公式结构本身， 或可能将预测模型复杂化， 能提升多少预报性能是未知的， 学术界对该方面的研究较少， 难度较大。（2）融合过多的其他要素逐时效数据， 往往需要庞大的数据支持， 在增加模型数据资源消耗的同时， 使模型结构复杂化不易于业务应用。由于本文篇幅所限， 下一步将针对如何在模型运行成本和订正性能之间取得平衡的问题进行拓展研究， 以进一步提高方法的订正能力。此外文本订正方法对改善模式误差的离散度方面效果有限， 相关方面需开展进一步研究。