高原气象

高原气象 >

2025 , Vol. 44 >Issue 2: 475 - 491

DOI: https://doi.org/10.7522/j.issn.1000-0534.2023.00085

基于宽度学习系统的云南省多源降水数据融合模型研究

  • 周媛媛 , 1, 2 ,
  • 杨晓辉 , 2 ,
  • 肖天贵 1, 2
展开
  • 1. 成都信息工程大学云南自然灾害防御技术研发中心，云南 昆明 650034
  • 2. 成都信息工程大学大气科学学院，四川 成都 610225
杨晓辉（1988 -）， 男， 内蒙古满洲里人， 讲师， 主要从事降水数据融合和地震反演方法研究. E-mail：

周媛媛（1986 -）， 女， 重庆铜梁人， 讲师， 主要从事降水数据融合和反演方法研究. E-mail：

收稿日期: 2023-07-12

  修回日期: 2023-10-14

  网络出版日期: 2023-10-14

基金资助

云南省重点研发计划项目(202203AC100006)

成都信息工程大学科研基金资助项目(KYTZ202220)

收起

Multi-Source Rainfall Data Assimilation based on Broad Learning System over Yunnan Province

  • Yuanyuan ZHOU , 1, 2 ,
  • Xiaohui YANG , 2 ,
  • Tiangui XIAO 1, 2
Expand
  • 1. Yunnan R&D Institute of Natural Disaster on Chengdu University of Information Technology，Kunming 650034，Yunnan，China
  • 2. College of Atmospheric Sciences，Chengdu University of Information Technology，Chengdu 610225，Sichuan，China

Received date: 2023-07-12

  Revised date: 2023-10-14

  Online published: 2023-10-14

Copyright

© Editorial Department of Plateau Meteorology （CC BY-NC-ND）
Fold

摘要

准确的降水量是精准预报降水引发的相关灾害的前提条件和基础， 因此， 获取准确的降水量显得十分必要。为此， 本研究搭建了一个基于宽度学习系统（Broad learning system， BLS）的多源降水融合模型， 以获取更准确的降水数据。以云南省为研究区域， 选用2014年4月至2017年12月的3B42V7、 IMERG、 GSMaP、 CMORPH、 PERSIANN卫星数据以及雨量计数据作为源数据， 加入经纬度信息， 进行多源数据融合。留一年交叉验证法（Leave-one-year-out cross validation， LOYOCV）用于验证所提融合模型的性能， 并使用相关系数（Pearson’s correlation coefficient， CC）、 均方根误差（Root-mean square error， RMSE）、 平均绝对误差（Mean absolute error， MAE）、 纳什效率系数（Nash-Sutcliffe coefficient of efficiency， NSE）和克林-古普塔效率系数（Kling-Gupta efficiency， KGE）等统计指标量化在不同时空尺度上的融合降水量的准确性。同时， 分别对比了基于支持向量机（Support vector machine， SVM）和深度神经网络（Deep neural network， DNN）的融合模型， 评估了经纬度信息在所提融合模型中的效力。在LOYOCV中， BLS融合降水的日平均CC、 RMSE、 MAE、 NSE均优于5个卫星产品。在时间尺度上， 融合降水能够捕捉实际雨量计降水的时间趋势， 且能较准确地估计2017年云南省的暴雨量； BLS融合降水在雨季（5 -10月）和干季（11月到次年4月）均优于5个卫星产品中表现最好的CMORPH降水产品。在空间尺度上， 相比5个卫星产品， BLS融合降水能在大部分地区表现出最高的CC、 NSE以及最小的RMSE、 MAE。BLS融合模型对实际降水的模拟能力高于SVM融合模型， 且相对于DNN模型用时更短、 更高效。此外， 经纬度信息的加入能提升融合降水的准确性。总之， 考虑了经纬度信息的基于BLS的多源降水融合模型能够提升云南省降水量的准确性， 在多源降水数据融合领域有一定的应用价值。

关键词： 多源降水数据; 数据融合; 宽度学习系统; 经纬度信息

本文引用格式

周媛媛 , 杨晓辉 , 肖天贵 . 基于宽度学习系统的云南省多源降水数据融合模型研究[J]. 高原气象, 2025 , 44(2) : 475 -491 . DOI: 10.7522/j.issn.1000-0534.2023.00085

Abstract

The accurate estimation of rainfall is always a topic of concern， given its pivotal role in accurately predicting rainfall-related disasters.This study proposed a multi-source rainfall assimilation technology based on a broad learning system （BLS） to improve the accuracy of rainfall estimation.Yunnan Province， located in China's low-latitude plateau， was chosen as the geographical area of interest to establish a multi-source rainfall assimilation model within this region.In particular， the model utilizes five satellite-derived rainfall datasets （3B42V7， IMERG， GSMaP， CMORPH， PERSIANN） and the latitude and longitude information as the source data， and the ground-based rainfall gauge data serves as the reference data.The time span of all the datasets is from April 2014 to December 2017.A leave-one-year-out cross-validation （LOYOCV） method was applied to verify the performance of the established assimilation model， where statistical indicators including Pearson’s correlation coefficient （CC）， root-mean square error （RMSE）， mean absolute error （MAE）， Nash efficiency coefficient （NSE） and Kling-Gupta efficiency （KGE） were used to quantify the accuracy of assimilation rainfall at different spatiotemporal scales.Concurrently， assimilation models based on support vector machine （SVM） and deep neural network （DNN） were established to highlight the accuracy and efficiency of the BLS， respectively.Additionally， the effectiveness of the latitude and longitude information within the proposed assimilation model was examined.The results show that the daily average statistical index of assimilation rainfall based on BLS is better than that of the other five satellite-based products in LOYOCV.At the temporal scale， the proposed assimilation technique effectively reflects the temporal variations observed in gauge-recorded rainfall.Moreover， it can accurately estimate the rainfall amounts during rainstorms in Yunnan Province throughout 2017.It is worth noting that the rainfall data generated through the BLS method outperforms the CMORPH product （the most accurate one among the five satellite-derived rainfall products） in both rainy and dry seasons （May to October and November to April of next year， respectively）.At the spatial scale， BLS-based rainfall results in most areas of Yunnan Province showed higher CC and NSE as well as smaller RMSE and MAE than the satellite-based products.The evaluation of the assimilation models based on BLS， SVM， and DNN highlights that the BLS exhibits superior functional mapping capabilities compared to SVM and demands fewer computational resources than DNN.It is reasonable to conclude that the multi-source rainfall assimilation approach utilizing the BLS while incorporating latitude and longitude information can enhance the precision of rainfall estimates in Yunnan Province.The proposed method presents practical significance in multi-source rainfall data assimilation.

Key words： multi-source rainfall data; data assimilation; broad learning system; longitude and latitude

1 引言

降水在水文气象领域扮演着重要角色， 是地表水文过程和陆面过程的主要驱动源（李哲， 2015）。然而， 极端降水常常引发暴雨、 洪涝、 城市水浸等灾害， 给人民的生命财产安全造成了极大的威胁（贾何佳等， 2022； 黄慧君等， 2023； 肖贻青等， 2023）。因此， 十分有必要对降水量进行准确预报， 以预警预报相关灾害。然而， 准确的降水量是精确预警降雨相关灾害的前提条件和基础。通常地， 降水量可通过多种途径获得。地面雨量计是获取降水量的传统方法， 是人们获取准确的降水观测的有效方法。它以点带面， 一般以一个监测站记录的雨量代表了方圆数十到数百公里内的雨量真实值。然而， 我国幅员辽阔、 地形复杂， 难以实现雨量站大量且均匀的布置， 导致雨量站在我国东部的密度较高， 在西部密度相对稀疏。由于降水是随时空变化有着显著变异的气象要素， 在雨量站相对稀疏的地区（尤其是我国西部）， 以点代面的方式将会给相应地区的雨量估算带来巨大的误差（Kavetski et al， 2006； 尹雄锐等， 2006）。随着天气雷达和气象卫星相关技术的发展， 获取降水量的方式发生了革新。遥测降水技术可实现大范围的且时间连续的降水量的获取， 且其不受地形限制， 可弥补地面雨量计测雨的不足（胡庆芳， 2013； Sunilkumar et al， 2016； Ma et al， 2018）。基于此技术， 国内外发布了多种卫星降水产品： 如热带降水测量计划（Tropical rainfall measuring mission， TRMM）的后实时多卫星降水分析产品（3B42V7）和实时降水产品（3B42RT）（Huffman et al， 2010）、 全球降水测量计划多卫星降水联合反演产品（IMERG）（Huffman et al， 2012）、 美国气候预测中心使用形变技术获得的降水产品--CMORPH（Joyce et al， 2004）等。
然而， 基于遥感技术的降水产品的准确性时常受到多种因素的影响（如： 传感器性能、 反演算法、 云层性质等）， 导致获得的降水量误差较大（刘元波等， 2011）， 因此导致了卫星产品在不同时间尺度或空间尺度有着不同的表现。如： Shen et al（2010）评估了CMORPH、 在创建CMORPH中使用的基于微波估计的降水估计、 3B42V7、 3B42RT、 美国海军研究实验室融合的降水产品、 PERSIANN在中国大陆地区的表现， 发现这些产品的精度在湿润区和暖季相对较高， 同时发现CMOPRH能相对准确地捕捉我国降水的时空分布特征。Xu et al（2017）评估了IMERG和3B42V7产品在青藏高原的表现， 发现前者倾向于低估小雨量， 后者却高估了小雨量， 但在中国的中低纬度地区， IMERG和3B42V7却能获得相对较准确的降水量（Tang et al， 2016）。此外， Tang et al（2020）还评估了全球降水观测计划（GSMaP）（Ushio et al， 2009）的产品、 CMORPH和使用一种人工神经元网络技术获得降水产品（PERSIANN）（Ashouri et al， 2005）在整个中国区域的表现， 发现GSMaP的准确性在中国大部分地区均高于CMORPH， 但PERSIANN不及CMORPH准确性高； 相对于CMOPRH来说， PERSIANN-CDR能够估计出更高精度的冬季降水。可见， 一种降水卫星产品并不能保证一直优于另一种降水产品， 会根据评价时使用的时空尺度的变化而变化。因此， 为了获得时空分辨率高且准确性高的降水数据， 有必要开展多源降水数据的融合技术以获得兼具多种降水产品优势的降水数据。
为了得到更准确的且时空分辨更高的降水数据， 学者们开展了大量的研究工作。Xie and Xiong（2011）采用最优插值法将CMOPRH产品与基于地面雨量计的中国逐时格点降水数据进行融合实验， 得到了一套中国区域的空间分辨率为0.1o的降水产品。Foehn et al（2018）开发了一种基于伪交叉变差函数来计算克里金计算方法中的协同区域化的线性模型的方法， 估计原本均没有雨量站数据和雷达降水数据的地区的降水量， 并将该方法应用到了瑞士罗纳河的上游流域， 结果显示该方法即便在雷达数据较少的地区都比反距离权重法表现更优异。此外， 贝叶斯类算法在多源降水融合领域也得到了广泛的应用。如： Ma et al（2018）搭建了一个基于动态贝叶斯模型平均方法的多源降水融合网络用于融合来自青藏高原的多源降水数据（3B42RT、 3B42V7、 CMORPH、 PERSIANN）， 具体地， 首先使用最大期望法实现动态贝叶斯模型的权重最优化， 然后使用克里金插值法将权重插值到整个青藏高原， 最后将整个地区的雨量站的权重求和从而获得融合的降水数据。Wang et al（2019）提出了一种基于贝叶斯的格点积分法的多源数据融合模型， 主要用来修正青藏高原的多山地区的卫星降水数据， 经过该方法校正过的降水数据不仅能捕捉到降水随着地形变化的特征还能降低相应的不确定性。Zhou et al（2021）基于贝叶斯广义回归网络搭建了一个多源降水数据融合模型， 在该模型中， 将贝叶斯方法与广义回归网络相结合， 并使后验概率最大化求得模型中的参数， 从而得到降水估计及其不确定性， 使用该方法估计出了我国东南地区的2016年的精度更高的日尺度的降水数据。随着计算机技术的迅速发展， 机器学习方法在融合多源数据方面得到了广泛应用。如Xu et al（2019）利用人工神经网络融合了对应于柴达木盆地的遥感和地面观测降水数据， 在该网络中， 作者将地面观测降水数据作为目标值， 雨量站的高程、 经度、 纬度以及TRMM降水数据作为输入层， 隐藏层数设置为20， 使用Levenberg-Marquardt算法（Moré， 1978）来训练网络。Wu et al（2020）利用卷积神经网络提取源数据（卫星降水数据、 地面雨量计数据、 热红外图像数据）的空间特征， 然后使用长短时记忆网络提取空间特征组成向量的前后方向的时间依赖性， 最后通过两个连接的机器学习网络获得每一个时刻的融合降水估计值。
上述数据融合方法均在一定程度上提高了降水数据在有雨量站地区的精度， 但在雨量站稀疏的地区， 他们的表现却不尽相同。基于降水空间分布的插值类方法能获得空间连续且平滑效果好的降水产品， 并且该类方法的适用性广泛， 能在不同的空间尺度和地理环境中使用， 然而， 插值类方法极易引入估计误差， 尤其是在雨量站稀疏或分布不均匀的地区， 往往导致该地区准确度低的降水量估计。基于贝叶斯算法的多源降水融合技术能够为获得降水估计提供不确定性的度量， 且由于贝叶斯方法给出了参数的后验概率分布， 有助于更好地理解参数的取值范围以及不确定性的程度， 但是贝叶斯类方法需要预先确定先验分布， 不同的先验分布会导致不同的降水估计的结果。此外， 贝叶斯类方法往往涉及到复杂的数学计算， 尤其是面对高维度或复杂的模型时， 该类方法面临着高计算复杂度， 从而影响计算效率， 限制其在实际中的应用。基于机器学习的方法在降水数据融合的领域的成功应用， 为我们提供了新的思路。这类方法尤其是作为机器学习方法代表之一的深度学习有着强大的映射能力， 能够有效模拟输入输出之间的复杂关系。然而， 深度学习网络结构中的复杂的层级结构为计算带来了巨大的开销， 尤其是在构建多源数据融合模型时， 需要海量的数据作为模型的输入输出数据， 无疑计算成本巨大， 严重影响模型的计算效率。
宽度学习系统（Broad learning system， BLS； Chen and Liu， 2017）的基本结构是单层神经网络， 通过增加宽度属性而非深度属性来增强其对复杂关系的映射。因此， 宽度学习方法拥有与深度学习一样强大的映射能力， 却比深度学习具有更高的效率。鉴于宽度学习方法的优异性能， 其已被应用到了各个领域， 如面部特征识别（Zhang et al， 2018）、 机械事故诊断（Zhao et al， 2019）、 高光谱图像分类（Zhao et al， 2021）、 面波反演（Yang et al， 2022）等。目前， 宽度学习方法在多源降水数据融合领域仅有过一次探索（Zhou et al， 2022）， 且主要以我国东南地区的降水作为目标， 并未探索基于宽度学习的多源降水融合技术在我国西南地区（以云南省为例）的融合效率。
综上所述， 本研究以云南省为研究区域， 选用5种卫星降水产品（3B42V7、 IMERG、 GSMaP、 CMORPH、 PERSIANN-CDR）、 地面雨量计数据、 雨量计经纬度数据， 基于BLS方法的理论搭建一个新的多源降水融合模型， 以期获得针对该区域精确度高且时空分辨率高的降水数据。本研究将设计留一年交叉验证（Leave-one-year-out cross validation， LOYOCV）方法验证该模型， 并使用皮尔逊相关系数（Pearson’s correlation coefficient， CC）、 均方根误差（Root-mean square error， RMSE）、 平均绝对误差（Mean absolute error， MAE）、 纳什效率系数（Nash-Sutcliffe coefficient of efficiency， NSE）量化LOYOCV中得到的降水量的在不同的时间和空间尺度上准确性。同时， 本研究将搭建一个基于支持向量机（Support vector machine， SVM； Joachims， 1998）的多源降水融合模型， 并使用上述4个统计指标和克林-古普塔效率系数（Kling-Gupta efficiency， KGE）量化估计降水的准确性， 将此结果与所提融合模型进行对比， 以进一步评估所提融合方法的性能。此外， 本研究还将搭建两个基于深度神经网络（Deep neural network， DNN）的多源降水融合模型， 以对比DNN和BLS在多源降水融合模型中的效率。

2 研究区域、 数据来源与研究方法

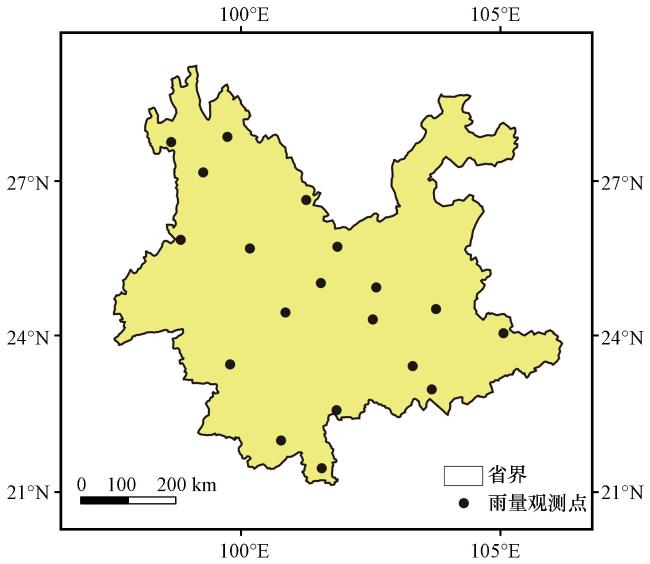
2.1　研究区域

云南省（97°31′E-106°11′E， 21°8′N-29°15′N）位于我国的西南边陲［图1， 该图及文中涉及的地图是基于中华人民共和国自然资源部地图技术审查中心标准地图服务系统下载的审图号为GS（2019）1821号的标准地图制作， 底图无修改］， 东临贵州省， 北靠四川省。云南省的地形复杂、 地理环境多变， 导致其辖区内的气候各异（晏红明等， 2023）。研究区域由于位于赤道附近， 日照充足， 且气候温和， 但其有着明显的季节变化特征， 且四季分明。该地区的降水特征显著， 受到地形因素影响显著， 其降雨主要集中在夏季， 一般将5 -10月定为雨季， 11月到次年4月为干季。近年来， 在气候变化加剧的背景下， 该地区降水空间分布变得更加不均匀， 导致干旱、 洪涝灾害等极端气象事件发生频率的增加。
图1 研究区域及雨量观测站的空间分布

Fig.1 The study area and the spatial distribution of gauges

2.2　数据来源

本研究使用5个卫星降水产品作为融合模型的数据源， 其详细信息如表1所示。其中， 3B42V7是通过地球静止红外数据和近地轨道微波测量反演， 并使用地面雨量计数据进行校正而得到的（Huffman et al， 2007）， 其时、 空分辨率分别为3 h和0.25°。IMERG数据是采用交叉校准、 合并、 结合雨量计数据与多卫星数据进行插值得到的（Huffman et al， 2015）。截至目前为止， IMERG有多个版本的数据可供选择， 本研究选用的是近实时Late Run的V6降水数据， 时空分辨率分别为0.5 h和0.1°。3B42V7和IMERG数据均可从戈达德地球科学数据和信息服务中心（GES DISC）获取。GSMaP数据是基于卡尔曼滤波器的移动矢量方法获取的降水数据， 具有较精细的空间分辨率（0.1°）， 多个时间分辨率可供选择， 本研究选用时间分辨率为24 h， 该数据可从日本宇航研究开发机构（JAXA）下载。CMORPH降水数据（简称CBLD）是基于形变技术反演得到的降水数据（Joyce et al， 2004）， 开始时间为1998年1月， 本研究选用的CMOPRH降水数据的时空分辨率分为24 h和0.25°。PERSIANN-CDR（简称PCDR）降水数据采用自适应人工神经元网络融合PERSIANN降水数据和全球降水气候计划的月尺度的降水产品而得到， 本研究选用的数据时空分辨率为24 h和0.25°， 该数据可从美国加利福利亚大学的水文气象与遥感中心（CHRS）获取。此外， 地面雨量计数据是由雨量计分别在08:00（北京时， 下同） -20:00和20:00至次日08:00两个时间段记录得到的降水数据， 由中国气象数据服务中心提供， 所用雨量计的经纬度信息亦可从该中心获取。
表1 多源降水数据源的详细信息

Table 1 Specific information of multi-source rainfall data

降水数据 时空分辨率 时间跨度 范围 数据来源
3B42V7 3 h/0.25° 1998年1月至今 50°S -50°N GES DISC
IMERG 0.5 h/0.1° 2000年6月至今 90°S -90°N GES DISC
GSMaP 24 h/0.1° 2014年4月至今 60°S -60°N JAXA
CBLD 24 h/0.25° 1998年1月至今 90°S -90°N Joyce et al， 2004
PCDR 24 h/0.25° 1983年1月至今 60°S -60°N CHRS
雨量计数据 12 h/不规则分布的点 1951年至今 中国 中国气象数据服务中心

2.3　研究方法

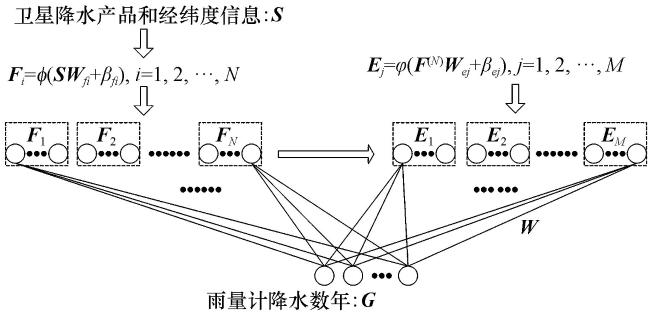
2.3.1　基于宽度学习的多源降水数据融合技术

本研究基于宽度学习系统搭建了一个新的多源降水融合网络， 如图2所示。假设卫星数据 S 和雨量计数据 G 的未知关系可用 Γ ( · )表示：
G = Γ ( S )
式中： G = [ g 1 , g 2 , … g N g ] T ∈ R N g × 1以及 S = [ S 1 , S 2 , … S N g ] T ∈ R N g × N s； g 1 , g 2 , … g N g表示 G 中包含Ng个雨量计数据样本； S 1 , S 2 , … S N g表示 S 中包含了Ns个（包括卫星降水产品的个数以及经纬度两个地理因子的个数）源数据， 本研究中Ns为7。
图2 宽度学习网络示意图

Fig.2 Schematic diagram of BLS framework

将图2中的 S 和 G 分别设定为训练融合模型的输入和输出， 那么估计的降水 G ^可表示为式（2）（Chen and Liu， 2017）：
G ^ = A W
式中： W是未知矩阵， 它包含了BLS的连接权重， 可实现输入层与输出层的连接； A是源于 S 的矩阵， 是一个转换特征矩阵， 它包含了从输入数据提取的特征以及这些特征经非线性激活函数后的表征输入数据特征多样性的增强特征， 可用式（3）（Chen and Liu， 2017）表示：
A ≡ [ F ( N ) , E ( M ) ] ≡ [ F 1 , F 2 , … F N , E 1 , E 2 , … E M ]
式中： F i = ϕ ( S W f i + β f i )， i=1， 2， …， N可表示第i个映射特征层， 每个特征层含有k个节点， E j = φ ( F ( N ) W f i + β f i )， j=1， 2， …， M表示第j个增强节点； ϕ ( · )和 φ ( · )分别是映射特征层的函数和非线性激活函数（本研究选用tanh（·）作为激活函数）， 根据Chen and Liu（2017）， ϕ ( · )可使用稀疏自编码实现。 W f i ( W e j )和 β f i ( β e j )分别是随机权重项和随机设置的偏置项； N是映射特征层组数， 它表征的是从输入数据提取的特征的个数， M是增强节点的个数， 表示前述特征层经过非线性激活函数的次数， 当N和M的个数越多， 意味着提取的数据特征越多， 特征多样性越强， 模型的非线性映射能力越强； 从转换特征矩阵 A 内的映射层组和增强节点的排列形式可知， 无论是映射层中节点数的增加还是增强层中节点的增加， 均以横向扩展的方式增加节点数， 这是宽度学习系统方法与深度学习方法最大的区别， 也是宽度学习方法效率更高的基础。
给出训练数据 G， 连接矩阵 W 可通过计算伪逆 A+ 的岭回归（Hoerl and Kennard， 1970）来实现：
W = A + G = ( A T A + λ I ) - 1 A T G
式中： λ是W的调整参数， 用于约束W； I是单位矩阵。当k、 N和M给定时， 估计的输出 G ^可通过将式（4）和式（3）代入到式（2）中得到。显然， 当融合模型中设置了不同的节点（k、 N和M）组合时， 会得到不同的估计值。此外， 连接矩阵W的计算只需在给定节点组合时计算一次， 这有别于深度学习方法中针对每一个神经元均需优化权重矩阵的方式（Hammerstrom， 1993）， 在很大程度上提高了宽度学习方法的效率。Chen and Liu（2017）指出， 可使用网格搜索法一步一步地搜索最优节点组合。本研究在训练融合模型的过程中， 采用最小的均方根误差在节点组合［1∶1∶30］×［1∶1∶20］×［1∶1∶120］中选择最优节点组合。

2.3.2　统计指标

本文使用前人研究（Ma et al， 2018； Tang et al， 2020； Wang et al， 2020； Wu et al， 2020）中常用到的四种统计指标（即： CC、 RMSE、 MAE和NSE）量化所提多源降水融合模型的准确性。CC表示融合降水量与地面雨量观测站降水量之间的线性相关程度， 其范围在［-1， 1］， 其绝对值越接近1， 说明二者之间的线性相关程度越强， 融合的降水量越准确。RMSE和MAE分别表示融合降水量以雨量观测站降水量为基准的偏离程度， 其取值范围均在［0， +∞）， 取值越小， 说明融合降水量越准确。NSE常用于描述估计值对真实值的模拟能力， 范围为（-∞， 1］， 该值越接近1， 表明融合模型对雨量计数据的准确模拟能力越强， 融合模型越可靠。此外， KGE是一种结合了相关系数、 偏置比、 模拟均值的较全面的评估模型模拟能力的统计指标（如式5所示）， 取值范围为（-∞， 1］， 本研究使用其评估SVM融合模型和本文所提模型的模拟能力。
K G E = 1 - ( C C - 1 ) 2 + σ ^ σ - 1 2 + μ ^ μ - 1 2
式中： σ ^和 μ ^分别为降水量估计值的标准差和均值； σ和 μ地面雨量计降水量的标准差和均值。

2.3.3　验证融合模型的方法

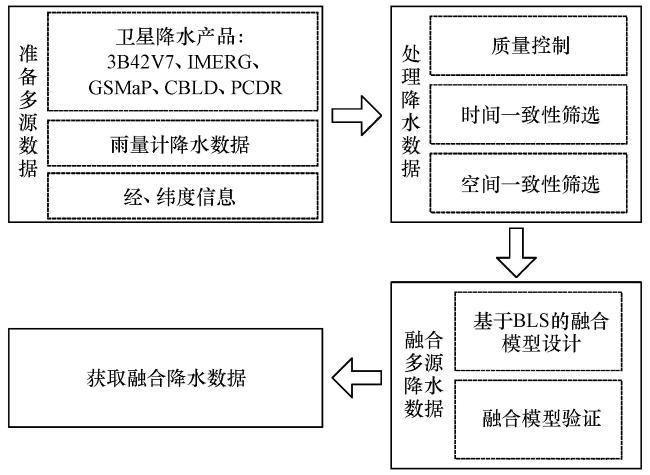
由于降水时间序列具有季节性特征和趋势性， 导致融合模型可能在某个时间段上存在过拟合的情况。因此， 为了避免这种情况的发生， 本研究设计了LOYOCV方法来验证所提的多源降水融合模型在不同时间段上的时间泛化能力。具体地， 本研究使用年份来划分降水数据对应的时间段， 即： 在2014 -2017年中， 选择云南省内所有雨量计在其中三年的日降水数据用于训练所提融合网络， 剩余一年的研究区内所有雨量计降水数据用于验证该融合模型， 该过程被重复4次。在每一次LOYOCV中， 均使用CC、 RMSE、 MAE和NSE来量化所提模型得到的融合降水值的准确性， 若CC和NSE（RMSE和MAE）大于（小于）本文所使用的任意一种卫星产品对应的统计指标， 则认为所提模型能够提高融合降水量的准确性。

2.3.4　基于宽度学习的多源降水数据融合方法的流程

本研究搭建的基于BLS的多源降水数据融合模型的主要流程如图3所示。首先， 准备多源数据。本研究主要使用5种日尺度的卫星降水产品包括3B42V7、 IMERG、 GSMaP、 PCDR、 CBLD和一种日尺度的地面雨量计数据及其对应的经纬度信息， 时间跨度为2014年4月至2017年12月。其次， 处理多源数据， 主要包括质量控制、 时空一致性筛选。质量控制主要包括异常值的剔除以及缺失值的补齐。本研究中， 若一个台站连续30天均未记录到降水量， 则将该台站剔除； 若台站的降水量仅是断续缺失， 则使用缺失值前后5天的降水量的均值进行补齐。由于本研究以地面雨量计数据作为参考数据， 因此需要将格点卫星降水数据通过反距离权重法将其调整为与雨量计数据一致的空间分布， 并剔除所有降水数据中的坏值， 并调整成时间一一对应的降水数据。由于国际交换台的降水数据已被用于本文所用的卫星产品的校正， 因此这些雨量计数据亦需一并剔除。经过数据处理后， 在云南省共计19个雨量计对应的数据用于本研究。 再次， 搭建基于BLS的多源降水融合模型， 并使用留一年交叉验证法验证该模型。设置该融合网络的节点组合为［1∶1∶30］×［1∶1∶20］×［1∶1∶120］， 使用19个雨量计在2014 -2016年对应的所有的降水数据作为训练数据， 剩余的2017年的数据作为验证数据， 使用最小RMSE在训练过程中寻找一组最优节点组合。设置同样的节点组合， 将验证数据选择为2016年的， 剩余年份的数据作为训练数据， 以此类推， 将研究时段内所有年份的数据都作为验证数据后， 意味着完成了针对BLS的多源降水融合模型的留一年交叉验证。最后， 使用各种统计指标从不同的时空尺度上去量化所提方法得到的融合降水的准确性， 进而获得可靠的融合降水数据。
图3 基于BLS的多源降水融合模型流程图

Fig.3 Flowchart of multi-source precipitation assimilation based on BLS

3 基于宽度学习的多源降水融合方法的表现

为了验证所提方法的有效性， 本研究使用了留一年验证法进行交叉验证， 使用CC、 RMSE、 MAE、 NSE量化融合降水的准确性。表2展示了四个统计指标在每一年的对应于19个台站的日平均值。总体来说， 无论是以哪一年的降水数据验证所提模型， 相比于卫星源数据， 所提的融合模型均能获得最优的统计指标（表中进行了加黑标注）。其中， 在所有用于验证融合模型的年份中， 基于BLS的融合降水的日平均CC均超过了0.83， NSE均超过了0.67， 均优于5个卫星产品在对应年份的表现。同时， 通过此表评估了卫星降水产品在云南省的表现。在所有卫星产品中， CBLD总能获得最优的统计指标， 其次是IMERG卫星产品， 接下来是3B42V7和GSMaP， 表现最差的是的PCDR。该评估结果可为学者选择针对云南省的卫星产品时提供参考。为了避免重复展示， 后续的融合模型的表现评估均是基于2017年的数据作为融合模型的验证数据进行的。
表2 留一年验证方法中的日平均统计指标

Table 2 The daily mean statistical metrics of assimilating rainfall data in LOYOCV

年份 降水产品 （序号） CC RMSE /mm MAE /mm NSE
2014 3B42V7（1） 0.676 6.659 2.784 0.369
IMERG（2） 0.724 6.214 2.377 0.455
GSMaP（3） 0.660 6.738 2.556 0.324
CBLD（4） 0.820 4.717 1.918 0.652
PCDR（5） 0.416 8.651 3.661 -0.200
BLS（6） 0.833 4.600 1.834 0.687
2015 3B42V7（1） 0.704 6.657 2.830 0.341
IMERG（2） 0.731 6.217 2.471 0.465
GSMaP（3） 0.660 7.187 2.725 0.233
CBLD（4） 0.848 4.336 1.799 0.665
PCDR（5） 0.505 8.084 3.530 -0.063
BLS（6） 0.853 4.324 1.769 0.684
2016 3B42V7（1） 0.630 6.828 2.967 0.256
IMERG（2） 0.661 6.672 2.555 0.282
GSMaP（3） 0.582 7.377 2.793 0.138
CBLD（4） 0.825 4.539 2.000 0.650
PCDR（5） 0.437 8.045 3.584 -0.056
BLS（6） 0.831 4.505 1.976 0.671
2017 3B42V7（1） 0.621 6.934 3.092 0.242
IMERG（2） 0.647 6.749 2.704 0.306
GSMaP（3） 0.603 7.214 2.863 0.141
CBLD（4） 0.818 4.560 2.063 0.638
PCDR（5） 0.454 8.132 3.660 -0.062
SVM 0.638 6.887 2.498 0.303
BLS（6） 0.839 4.216 1.924 0.692
BLS-N 0.831 4.479 2.022 0.664
BLS-Stability 0.826 4.374 2.000 0.676

表中黑体代表最优统计指标； BL-N代表融合数据源中未加入经纬度信息； BLS-Stability代表使用更少样本加入到融合网络中

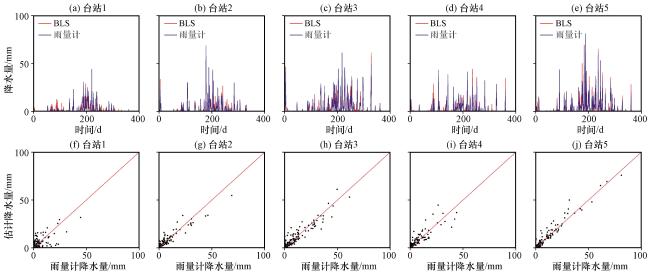
3.1　融合降水数据在时间尺度上的表现

本研究随机选择了云南省的19个雨量计中5个台站对应的融合降水在时间尺度上的表现。该部分以2017年的数据作为验证数据进行各个尺度上的评估。图4展示了随机选择的5个台站对应的2017年的融合降水数据与实际雨量计降水数据在时间尺度上的对比。从图4中的时间序列的对比可见， 对应于台站2、 台站3、 台站4、 台站5的融合降水均能与实测降水值较好地匹配， 尤其体现在BLS融合方法对暴雨量（日降水量≥50 mm）的较准确的捕获方面。从对应的散点图可知， 黑色圆点均围绕在红色对角线周围， 说明了基于BLS的融合降水数据对实际雨量计数据拟合较好， 说明了所提方法的准确性较高。总体而言， BLS融合降水能够捕捉实际雨量计降水的时间趋势， 且对2017年云南省的暴雨量的估计能力较强。
图4 2017年的对应于随机选择的台站1~5基于BLS的融合降水与实际雨量计降水的对比（a~e）及其对应的散点分布（f~j）

Fig.4 The comparison between BLS-based rainfall data and gauge-based rainfall data （a~e） and their corresponding scatter plots （f~j） at Station 1~5 in 2017

从图4（a）~（e）可知， 云南省的降雨多集中在雨季（5 -10月）， 在干季（1 -4月、 11月、 12月）降雨相对较少， 因此， 为了更清晰地展示所提方法在云南省的雨季和干季的表现， 本研究给出了融合降水量在这两个时间尺度上的统计指标（图5）。从图5（a）可知， 相对于卫星降水产品， BLS无论是在雨季还是干季均能获得更高的相关系数， 分别为0.817（雨季）和0.845（干季）， 表现次之的是CBLD， 最差的是PCDR。融合降水与卫星降水在RMSE和MAE上有着相似的表现， 但仍是BLS融合降水数据在雨季和干季均有着小差的误差。在雨季， BLS融合降水的RMSE和MAE分别为5.281 mm和2.802 mm； 在干季， RMSE和MAE分别为2.554 mm和1.025 mm， 均比在卫星产品中表现最好的CBLD降水量的误差小。从图5（d）可见， 在雨季和干季， BLS融合降水的NSE分别为0.667和0.437， 相比于其他5个降水产品， BLS融合模型能最准确地模拟实际降水量， CBLD降水产品的实际降水模拟能力虽然较BLS弱， 但仍是5个卫星降水产品中表现最佳的。纵观卫星产品和融合降水在雨季和干季的表现， 4种降水数据的CC值在干季比在雨季高， 但所有降水数据的NSE在雨季比在干季更高， 说明所有的降水产品在雨季能更好地模拟实际降水量。
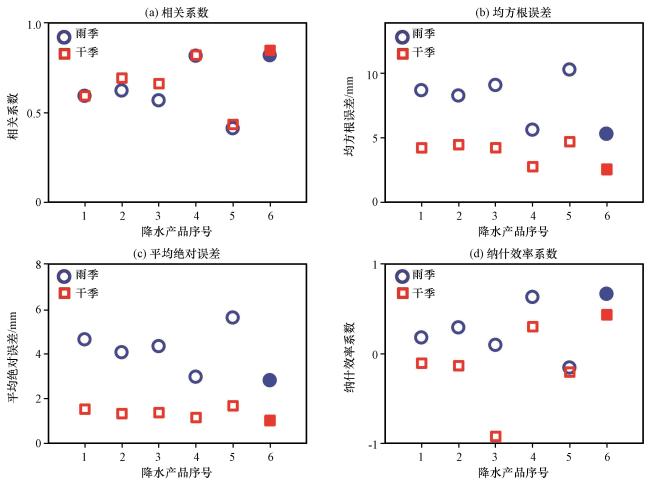
图5 融合降水在雨季和干季的CC（a）， RMSE（b）， MAE（c）， NSE（d）与其他5个卫星降水产品相应的统计指标对比

横轴的1~6分别代表3B42V7、 IMERG、 GSMaP、 CBLD、 PCDR、 BLS； 实心符号代表最优统计指标

Fig.5 The comparison of assimilating rainfall data and satellite-based rainfall data on CC （a）， RMSE （b）， MAE （c）， NSE （d） in rainy season and dry season.The numbers of 1~6 on the horizontal axis stand for 3B42V7， IMERG， GSMaP， CBLD， PCDR， and BLS-based precipitation products； The solid symbol stands for the optimal statistical metrics

3.2　融合降水数据在空间尺度上的表现

为了从不同的角度验证所提融合方法的有效性， 本研究计算了所提方法的融合降水在云南省的19个台站的4个日统计指标， 并与其他5个卫星产品进行了对比， 如图6所示。该图展示了4种统计指标的空间分布， 并使用颜色的深浅表示了统计指标的优劣程度， 图中每一列共计6个子图， 分别表示6种降水产品在CC、 RMSE、 MAE和NSE等统计指标的表现。同时， 统计了各个降水产品表现最优的统计指标的台站数（表3）。首先， 针对CC（图6第1列）， 除了PCDR， 其他降水数据均能在相应台站获得较高的CC值， 其中BLS表现最好， 其次是CBLD， 根据表3可知， 他们分别能在15和4个台站获取最高的CC。CBLD主要位于云南省的中部和西北部获得相对较小的CC， 而BLS仅在云南省中部个别台站表现较CBLD差。在RMSE方面［图6（b）， 即图6第2列］， PCDR表现最差， 尤其是在云南省南部地区， PCDR的降水数据相对于其他降水数据来说有着更大的误差。在此统计指标上， 表现最好的仍是BLS， 其次是CBLD， 他们分别在16个和3个台站获得了最小RMSE（表3）。在平均绝对误差方面［图6（c）， 即图6第3列］， 所有的降水数据均在云南省的南部并靠近省边界的地方表现出较大的误差。此外， BLS能获得最优MAE的所对应的台站数是8， 其次是IMERG与CBLD均为5个台站， 最后是GSMaP为1个台站， 说明BLS的降水数据在MAE方面仍能表现最好， IMERG与CBLD表现大致相似。在NSE方面［图6（d）， 即图6第4列］， GSMaP和PCDR在云南省的中部出现了负值， 表明他们在该地区对地面雨量计降水量模拟能力欠佳。其他降水数据的NSE在大多数的地方都接近1， 尤其是基于BLS的融合降水数据， 在16个台站都获得了最大的NSE值， 其次是CBLD在3个台站获得最优NSE， 说明了BLS融合降水数据能较好地模拟地面实际降水。
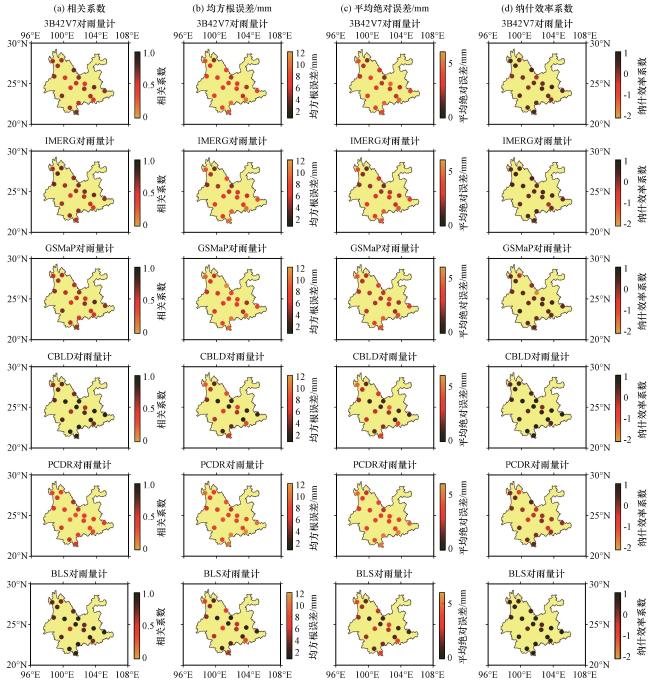
图6 卫星降水产品和融合降水数据在每一个台站对应的CC（a）， RMSE（b， 单位： mm）， MAE（c， 单位： mm）， NSE（d）的空间分布

图中圆点的颜色越深表示该测站的估计的降水量越准确

Fig.6 The spatial distribution of CC （a）， RMSE （b， unit： mm）， MAE （c， unit： mm）， NSE （d） at each site of satellite-based and BLS-based rainfall data.The darker the color of the dots， the more accurate the estimated precipitation at the corresponding gauge stations

表3 各个降水产品获得优异统计指标的台站数

Table 3 The number of sites corresponding to satellite-based and BLS-based rainfall data with the best statistical metric

降水产品/统计指标 3B42V7 IMERG GSMaP CBLD PCDR BLS
CC 0 0 0 4 0 15
RMSE 0 0 0 3 0 16
MAE 0 5 1 5 0 8
NSE 0 0 0 3 0 16

加黑字体代表最多台站数

经过上述评估， 不仅验证了基于BLS融合模型所得降水值较高的准确性， 同时还验证了本研究所用5种卫星降水产品在云南省内的不同的表现。总体来说， 在不同的时空尺度下， 5种卫星降水产品在云南省表现最好的是CBLD， 表现较差的是GSMaP和PCDR。CBLD卫星产品能在云南省获得最优异的表现在于其获得降水值的CPC形变技术以及使用了全球地面雨量计数据进行了校正（Shen et al， 2010； Joyce et al， 2004）。GSMaP表现相对较差， 可能是因为在处理原始数据和校正数据时仅使用了云运动矢量法和卡尔曼滤波方法导致具有较低准确性的降水估计（Liu et al， 2022）。PCDR表现较差的原因在于其仅基于红外传感器， 通过云顶温度间接计算降水， 红外传感器在监测弱降水和小水滴方面远不如微波传感器有效（Jiang et al， 2021）。

4 讨论

4.1　与SVM融合降水对比

本研究搭建了一个基于SVM多源降水融合模型， 以与BLS融合模型进行对比。为了与前述评估使用的验证数据保持一致， 本研究使用2017年的数据作为验证数据来验证SVM融合模型， 使用2014 -2016年的卫星数据、 雨量计数据和经纬度信息训练该模型。使用与BLS融合模型相同的多源降水数据以及经纬信息计算了2017年的基于SVM的融合降水数据， 并计算了4个日统计指标， 将其与BLS融合降水的相应统计指标进行了对比， 如图7所示。在该箱线图中， 每一个箱子从下至上分别是最小值、 第25分位值、 第50分位值、 第75分位值、 最大值。从图7中可知， SVM融合降水的四个统计指标的任何一个分位点值均高于（RMSE和MAE）或低于（CC和NSE）BLS对应的统计值指标， 尤其是SVM对应的NSE值最大为0.528， 远小于BLS对应的最大值（0.939）， 说明SVM在提升融合降水的准确性方面不及BLS。此外， 本研究计算了基于SVM的融合降水数据在2017年的19个台站的日平均统计指标（表2）， 发现各项指标均不及BLS， 甚至比源数据如CBLD更差， 表明SVM对复杂函数关系的模拟能力并不及BLS。图8给出了分别通过SVM和BLS融合模型得到2017年的云南省的19个台站的日降水估计的KGE的空间分布， 以更全面地评估和对比这两种融合模型的准确性和模拟能力。基于SVM融合模型得到降水估计的最大KGE出现在云南省的中部地区， 最小值出现研究区域的边界， KGE值的变化范围在［-0.014， 0.392］， 均小于对应BLS融合模型得到的KGE值（范围为［0.474， 0.903］）。此外， 基于BLS得到的KGE值仅有两个值小于0.5， 而基于SVM的KGE所有值均小于0.5， 说明BLS融合模型的综合表现远优于SVM。为了对比两种融合模型在不同时空尺度上的表现， 本文给出了由两种融合模型得到的2017年的在云南省的日均降水量的空间分布（图9）。以地面雨量计的日均降水量为基准， 基于SVM的融合模型几乎低估了每一个台站对应的日均降水量， 而BLS融合模型的日均降水量更接近雨量计降水。从雨量计的日均降水量的空间分布来看， 较大的日均降水量出现在云南省南部， 较小降水量出现在该地区的中部与北部， 与基于BLS融合模型刻画的日均降水量的空间分布高度相似。总而言之， 无论在表征相关性、 误差、 模拟能力方面， 还是对日均降水量的空间分布的刻画方面， 本文所提融合模型均优于基于SVM的融合模型。
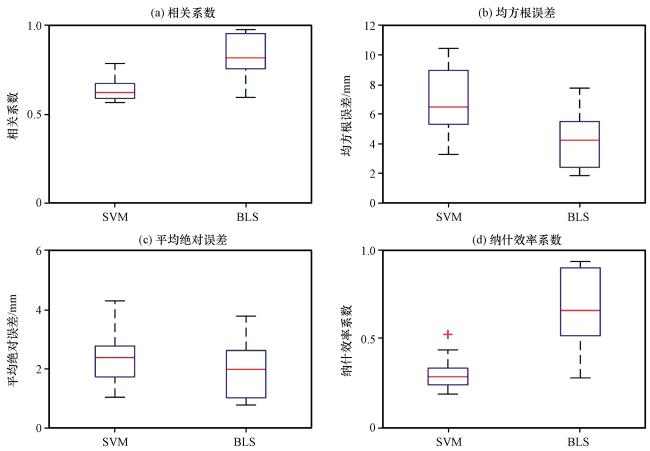
图7 基于SVM和BLS融合降水的CC（a）， RMSE（b）， MAE（c）， NSE（d）的箱线图

Fig.7 The boxplot of CC （a）， RMSE （b）， MAE （c）， NSE （d） of SVM- and BLS-based rainfall estimates

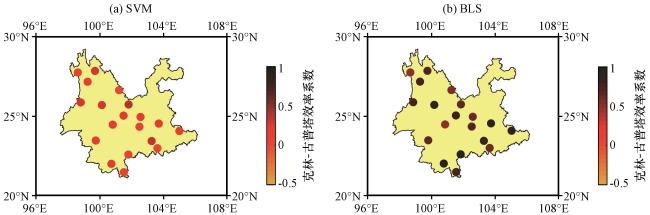
图8 基于SVM（a）和BLS（b）的融合模型的2017年在每一个台站的日降水量估计的KGE的空间分布

Fig.8 Spatial distribution of KGE estimated by daily rainfall based on SVM （a） and BLS （b） daily rainfall estimates at each site in 2017

图9 基于SVM融合模型（a）、 BLS融合模型（b）、 地面雨量计（c）的2017年日均降水量的空间分布

Fig.9 Spatial distribution of mean daily rainfall in 2017 based on SVM （a）， BLS （b） and gauges （c）

基于SVM的融合模型表现较差可能在于以下几方面的原因。首先， 在训练SVM融合模型之前， 需事先设置SVM方法的参数， 这些参数主要涉及到误差项惩罚系数、 核函数、 核函数系数值、 核函数最高次幂、 模型收敛参数、 最大迭代次数等， 其中， 误差项惩罚系数和核函数最高次幂的数值设置得越大， 模型越容易过度拟合。此外， 核函数有高斯核函数和sigmoid核函数可选， 用于实现数据的线性可分。可见， SVM融合模型能获得比较准确的降水量的前提是各类参数的正确设置以及核函数的正确选择， 而这些特征参数的正确设置和核函数的正确选择往往需要事先对数据特征的准确了解， 严重依赖于人为经验。其次， 基础的SVM算法主要思想是试图得到一个超平面来实现线性可分和部分线性可分问题， 而本文的处理对象为地面雨量计降水与多源降水数据及经纬度信息之间的极其复杂的函数关系， 并非简单的线性或部分线性关系， 而求解得到的单一的超平面无法很好地模拟该函数关系， 从而导致经SVM融合模型得到降水估计准确度不高。同时， 虽然SVM方法可以通过核函数来将数据从低纬映射到高维空间， 进而处理非线性问题， 然而， 正如本文提到的SVM方法在核函数的选择方面的局限性， 只有根据数据特征选择了正确的核函数的情况下， 才有可能实现复杂函数关系的模拟。此外， 在高维空间中进行模拟复杂函数关系时， 尤其是面对大量训练样本数据的情况， SVM融合模型的计算复杂度会迅速增加， 需要大量地计算资源和时间成本， 这也视为SVM方法在处理复杂函数关系时的局限性之一。再者， 本文使用的云南省的日降水数据多数集中在0~50 mm之间， 但亦有少部分数据超过50 mm， 这些少数样本在SVM算法中被视为异常值或噪声， 由于SVM中的凸优化问题是使支持向量与超平面之间的距离最大化， 而异常值或噪声的存在会导致得到的超平面发生变化， 从而影响优化结果， 进一步导致SVM算法对复杂函数关系的模拟能力变差， 使降水估计值不准确。相对于SVM方法的复杂的参数设置和核函数的选择， BLS方法在进行模型训练之前， 并不需要设置大量的参数， 仅需要给出节点组合的范围（在本研究中主要涉及到特征层的组数、 每个特征层中的节点个数以及增强节点的个数的范围）， 并不存在人为设置各种复杂参数的情况， 减少了人为经验对估计结果的干扰。同时， 多源降水数据融合模型的搭建往往需要海量的数据作为输入， 在处理大量数据的能力方面， 由于SVM使用的是线性或非线性核函数构建成的相对较简单的模型， 限制了其处理大量数据的能力， 而BLS方法通过横向增加映射特征层和增强节点个数的方式增加网络的复杂度， 节点组合中的个数越多表明网络越复杂， 高复杂度的网络可在大量数据中自适应的发现抽象特征和模式， 从而实现对海量数据的处理。此外， SVM方法在本研究中的实现过程主要是找到一个与训练数据点尽可能地接近超平面， 从而得到融合降水估计值， 其基本思想和结构与BLS方法的结构截然不同， BLS方法中不断动态横向增加的网络节点的方式能有效地提取不同数据的特征， 提高该网络对海量数据的表达能力， 进而实现对复杂函数关系较准确的模拟。

4.2　基于BLS与深度学习网络的降水融合模型对比

为了与时下流行的深度学习网络（Deep Neural Network， DNN； Yan et al， 2015）进行对比， 本研究搭建了两个基于DNN的多源降水融合模型， 用于估计融合降水。一般来说， DNN的网络结构复杂度对应着对函数关系的映射能力， 但过于复杂的网络结构不仅意味着模型可能存在过拟合的情况， 还面临着巨大的时间消耗。在此处引入DNN的目的， 是为了与BLS融合模型进行时间消耗的对比， 因此， 本研究设置了一个具有简单网络结构（DNN1）和稍复杂网络结构（DNN2）的DNN融合模型。即， DNN1的网络结构设置为3层， 每一层10个神经元； DNN2的网络结构为7层， 每一层亦为10个神经元。根据已有研究（Kuok and Yuen， 2020； Zhou et al， 2022）， Levenberg-Marquardt算法用于训练本研究搭建的基于DNN1和DNN2的融合模型。基于BLS的融合模型的节点组合设置为13个映射层组， 每个映射层含有19个节点以及120个增强节点。三个融合模型均在MATLAB平台上运行， 电脑配置RAM为16.0 GB， 处理器为Intel（R） Core（TM） i7-10750H CPU@2.60GHz 2.59 GHz。针对两个DNN融合模型， 使用与BLS融合模型一致的源数据（为了与前文评估BLS融合模型在不同时空尺度上的表现时使用的数据保持一致， 仍选用2014 -2016年的数据作为训练数据， 2017年的数据作为验证数据）， 结果如表4所示。从表4中可知， 相对于DNN2来说， DNN1所用训练时间更少， 为3.101 s， 但是准确性却相对较低（RMSE为4.922 mm）。DNN2获得的降水估计相对于DNN1来说更准确， 但是相对耗时， 因为DNN2的层级结构比DNN1更复杂。然而， 将两个DNN融合模型与BLS相比时， BLS能获得的准确性最高的融合降水（RMSE为4.216 mm）， 且用时最短（0.372 s）。表4中基于BLS和DNN的训练时间差别仅为秒级别的， 这样的时间消耗差别在实际应用中几乎是可以忽略的， 然而， 该效率对比是没有考虑网络复杂度选择的。值得注意的是， 实际应用中网络复杂度选择是建立有效预测网络的前提条件。当考虑网络复杂度时， 两种融合网络的时间消耗差别将是单个网络差别的累积， 累积的时间消耗将是无法忽略的。可见， 相较于DNN降水融合模型， 基于BLS的降水融合模型的效率更高、 更适用于实际应用。
表4 基于BLS和DNN的多源降水融合网络的效率对比

Table 4 Efficiency comparison of assimilating multi-source precipitation based on BLS and DNN

融合方法 训练时间/s RMSE/mm
DNN1 3.101 4.922
DNN2 6.714 4.829
BLS 0.372 4.216
根据Feng and Chen（2018）的研究， BLS与DNN均具备模拟复杂函数关系的能力， 面对同样的数据， 得到的估计值的准确度几乎一致， 但DNN的时间消耗总是比BLS高， 这与本研究的对比结果一致。虽然BLS和DNN是两种不同的神经网络， 二者均有神经网络架构的强大映射能力和泛化能力， 使得这两种网络在函数建模方面均有高性能表现。然而， 两种网络在计算效率方面表现出明显差异， 二者的网络结构差别是引起建模效率差别的根本原因。BLS构建单层神经网络， 通过提高网络的宽度复杂性提高网络的函数建模能力， 其网络权重的优化依赖于伪逆的计算， 而伪逆的计算时间消耗非常小， 且针对每一组节点组合仅计算一次网络权重， 保障了BLS的网络训练高效性； 相反， DNN构建多层神经网络， 通过增加神经网络的层数和每层网络的神经元数量提高网络的函数模拟能力， 每个神经元均涉及网络权重的优化， 庞大的神经元数量导致了DNN的网络训练低效表现。在实际应用中， 我们通常会面对样本维度变化、 样本数量变化、 研究区域变化等情况， 这些情况需要研究人员重新进行网络训练， 显然， 面对这样的实际情况， BLS利用神经网络的宽度复杂性代替深度复杂性这一特点可以节省计算开销、 提高工作效率， BLS相对于DNN的优势使其更适用于多源降水数据融合技术。若不考虑计算开销和时间消耗， 依靠BLS和DNN强大的映射能力， 二者在面临海量数据的多源降水融合领域均是不错的选择。

4.3　经纬度信息在融合模型中的作用

本研究的融合模型中除了加入降水数据外， 还加入了经纬度信息， 从而获得了准确性更高的融合降水。本研究亦测试了未加入经纬度信息的BLS融合模型的准确性（以2017年的数据作为验证数据为例）， 结果如表2所示。从表2中可知， 未加入经纬度信息的BLS融合降水的四个统计指标均比加入的略差， 但是总体来说比5个卫星产品的准确性高， 说明经纬度信息的加入有助于提升融合降水的准确性。降水具有空间异质性的特征， 表现为在不同地理位置（可使用经纬坐标表征）可能有着显著差别的降水量， 即， 降水的空间分布可能与地理位置有着某种相关关系。在BLS融合模型中加入与降水相关的经纬度信息能给模型训练提供更多的有效信息， 加之， BLS模型强大的复杂函数关系的映射能力， 使模型能够自适应地学习到地理位置与降水量之间的相关关系， 从而修正模型输出结果， 得到准确度再次提升的降水量估计值。同时， BLS融合模型在面对更多数据输入时仍能准确地模拟复杂的函数关系得到准确性提高的融合降水数据， 说明BLS有着强大的映射能力， 适用于有着海量数据作为输入的多源降水融合模型。除了经纬度信息外， 地形、 高程、 温度、 风速、 比湿等因子可能与降水量的大小相关（Bhuiyan et al， 2019）， 这些因子的加入亦有可能提升BLS融合降水量的准确性。理论上， 加入更多数据到融合模型的方式能进一步提升估计降水量的准确性， 同时， 亦要求融合模型具有更高的复杂度。因此， 在接下来的研究中， 除了考虑将更多的因子加入到针对云南省的多源降水融合模型中外， 还将采用相关方法评估将哪些因子加入到融合模型， 以平衡模型复杂度和估计降水量准确性之间的关系。

4.4　基于BLS的多源降水融合模型稳定性和泛化性分析

模型的稳定性评估衡量该模型是否能稳定估计准确降水量的重要指标， 为此， 本文设计了一个实例来验证所提模型的稳定性。在该实例中， 使用2014 -2016年的云南省的基于卫星的和地面雨量计的隔一天的日降水数据和经纬度信息作为BLS多源降水融合模型的训练集， 也就是说， 将用相对于前述提到的留2017年验证方法中的一半的训练样本用于该实例， 仍将2017年的云南省的对应于19个台站的日降水数据和经纬度信息作为验证集。BLS的节点组合仍设置为［1∶1∶30］×［1∶1∶20］×［1∶1∶120］， 经过模型训练， 最优节点组合为6×12×120， 有别于使用2014 -2016年的全部样本参与训练时的最优节点组合13×19×120。验证数据的日平均统计指标如表2所示。从表中可知， 该实例中的CC、 RMSE、 MAE和NSE分别为0.826、 4.374 mm、 2.000 mm、 0.626， 与使用全部样本参与训练得到的上述日统计指标分别相差1.55%、 3.61%、 3.80%、 2.31%， 最大的偏差未超过4.00%， 说明所提融合模型在训练样本减少的情况下能较准确估计降水量， 表明基于BLS多源降水融合模型具有较强的稳定性。
基于机器学习的模型的泛化性是评估该模型在未参与训练的数据上的表现能力的重要指标， 因此， 十分有必要对本文所提的基于BLS的多源降水融合模型的泛化性进行评估。虽然本文设计的留一年验证法亦能评估所提模型时间上的泛化能力， 但为了进一步地从更多的角度证明BLS模型的强的泛化性， 本文设计了一个不仅在时间上也在空间上独立的验证实验。在该实验中， 首先， 筛选出19个台站中的某一个台站在2014 -2017年对应的降水数据和经纬信息； 然后， 将剩余台站在2014 -2016年对应的降水数据和经纬度信息用于BLS融合模型的训练， 将前述筛选出的某一台站在2017年对应的数据用于模型的验证。表5给出了使用独立验证法得到的各个降水产品在筛选出的某一台站的2017年的日统计指标对比。从表中可知， 所提模型的降水估计无论是在与地面雨量计数据的相关系数上（CC=0.754）、 模拟雨量计数据的能力上（NSE=0.558）， 还是与参考数据的偏差上（RMSE=3.136 mm、 MAE=1.192 mm）均优于其他5个卫星产品在该台站的表现， 进一步证明了所提融合模型具有较强的泛化能力。
表5 各个降水产品在某一个台站的2017年的日统计指标

Table 5 Daily statistical indicators of six precipitation products at one site in 2017

降水产品 CC RMSE/mm MAE/mm NSE
3B42V7 0.632 4.371 1.800 0.141
IMERG 0.725 3.775 1.406 0.359
GSMaP 0.618 5.330 2.162 -0.277
CBLD 0.724 3.319 1.418 0.505
PCDR 0.439 6.328 2.551 -0.800
BLS 0.754 3.136 1.192 0.558

加黑字体表示最优统计指标

5 结论

本研究基于宽度学习方法搭建了针对云南省的多源降水融合模型， 在该模型中， 不仅考虑了5种卫星降水产品， 还加入了经纬度信息， 以提高融合降水的准确性。本研究设计了留一年交叉验证法验证该模型， 并利用5种统计指标量化融合降水在不同时间和空间尺度上的准确性， 且分别比较了该模型与基于SVM的融合模型以及基于DNN融合模型的性能和效率， 并探索了经纬度信息在所提模型中的效力， 得到以下主要结论：
（1） 在留一年验证中， 基于BLS的融合降水的日平均CC、 RMSE、 MAE、 NSE在2014 -2017年的任何一年都优于3B42V7、 IMERG、 GSMaP、 CBLD、 PCDR， 其中所有日平均CC均高于0.83， NSE均高于0.67。
（2） 在时间尺度上， BLS融合降水能够捕捉实际雨量计降水的时间趋势， 且能较准确地估计2017年云南省的暴雨量； 在雨季， BLS融合降水的CC、 RMSE、 MAE、 NSE分别为0.817、 5.281 mm、 2.802 mm、 0.666， 在干季这些统计指标分别为0.845、 2.554 mm、 1.025 mm、 0.437， 均优于5个卫星产品中表现最好的CBLD降水产品。
（3） 在空间尺度上， 相比5个卫星产品， BLS融合降水分别在19个台站中的15个台站、 16个台站、 8个台站和16个台站表现出最高的CC、 NSE以及最小的RMSE、 MAE。
（4） 基于BLS的融合降水的准确性以及对实际降水的模拟能力高于基于SVM的融合数据， 尤其是SVM对应的NSE和KGE（最大值分别为0.528和0.392）远小于BLS得到的最大值（分别为0.939和0.903）。与两个含有不同层数和神经元的DNN融合模型对比时， 在相同输入数据条件下， 基于BLS的融合模型所用时间更短， 说明所提融合模型的效率更高。
（5） 经纬度信息加入到降水融合模型中能提升降水数据的准确性。
基于BLS融合模型得到降水量的准确性在不同的时空尺度上均高于5个卫星降水产品以及基于SVM融合模型得到的降水估计值， 且所提融合模型的效率远高于基于DNN的融合模型。同时， 所提融合模型在输入样本减少一半的情况下， 仍能较准确的估计降水量， 说明了该模型有着较强的稳定性。经过独立验证的结果论证了BLS融合模型较强的泛化能力。基于BLS融合模型在各方面的优异表现， 使后续使用文中已搭建的融合模型生成准确度高、 时空分辨率更高的针对云南省甚至包括云南省周边地区的降水数据产品成为可能。此外， 本文所提模型中加入的与降水相关的经纬度信息， 提高了降水估计的准确性。因此， 在接下来的研究中， 可在BLS融合模型中加入更多的与降水相关的气候或地形因素（如： 温度、 风速、 比湿、 高程等）以期更进一步地提高融合降水量的准确性。此外， 更多气候或地形因素加入到BLS融合模型中意味着模型面临着更多的数据输入， 在接下来的研究中， 将探索平衡模型计算开销与估计准确性之间关系的方法。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
Ashouri H， Hsu K L， Sorooshian S， et al， 2015.PERSIANN-CDR： Daily precipitation climate data record from multisatellite observations for hydrological and climate studies［J］.Bulletin of the American Meteorological Society， 96（1）： 69-83.DOI： 10. 1175/BAMS-D-13-00068.1 .

Bhuiyan M A E， Nikolopoulos E I， Anagnostou E N， 2019.Machine learning-based blending of satellite and reanalysis precipitation datasets： a multiregional tropical complex terrain evaluation［J］.Journal of Hydrometeorology， 20（11）： 2147-2161.DOI： 10. 1175/JHM-D-19-0073.1 .

Chen C P， Liu Z L， 2017.Broad learning system： an effective and efficient incremental learning system without the need for deep architecture ［J］.IEEE Transactions on Neural Networks and Learning Systems， 29（1）： 10-24.DOI： 10.1109/TNNLS.2017. 2716952 .

Feng S， Chen C P， 2018.Fuzzy broad learning system： a novel neuro-fuzzy model for regression and classification［J］.IEEE transactions on cybernetics， 50（2）： 414-424.DOI： 10.1109/TCYB. 2018.2857815 .

Foehn A， Hernández J G， Schaefli B， et al， 2018.Spatial interpolation of precipitation from multiple rain gauge networks and weather radar data for operational applications in Alpine catchments ［J］.Journal of Hydrology， 563： 1092-1110.DOI： 10.1016/j.jhydrol.2018.05.027 .

Hammerstrom D， 1993.Neural networks at work［J］.IEEE spectrum， 30（6）： 26-32.DOI： 10.1109/6.214579 .

Hoerl A E， Kennard R W， 1970.Ridge regression： biased estimation for nonorthogonal problems［J］.Technometrics， 12（1）： 55-67.DOI： 10.1080/00401706.1970.10488635 .

Huffman G J， Adler R F， Bolvin D T， et al， 2010.The TRMM Multi-Satellite Precipitation Analysis （TMPA） in satellite rainfall applications for surface hydrology［M］.Dordrecht： Springer.DOI： 10.1007/978-90-481-2915-7_1 .

Huffman G J， Bolvin D T， Braithwaite D， et al， 2015.NASA Global Precipitation Measurement （GPM） Integrated Multi-satellite Retrievals for GPM （I-MERG）.Algorithm Theoretical Basis Doc.（ATBD）， version 4.5， Greenbelt， MD， 26 pp.［2023-07-12］.

Huffman G J， Bolvin D T， Braithwaite D， et al， 2012.Developing the integrated multi-satellite retrievals for GPM （IMERG）［C］.In EGU General Assembly Conference Abstracts.Austria： Vienna， 6921.

Huffman G J， Bolvin D T， Nelkin E J， et al， 2007.The TRMM Multisatellite Precipitation Analysis （TMPA）： Quasi-global， multiyear， combined-sensor precipitation estimates at fine scales［J］.Journal of Hydrometeorology， 8（1）： 38-55.DOI： 10.1175/JHM560.1 .

Jiang X， Liu Y， Wu Y， et al， 2021.Evaluation of the performance of multivsource precipitation data in southwest China［J］.Water， 13（22）： 3200.DOI： 10.3390/w13223200 .

Joachims T， 1998.Making large-scale SVM learning practical［R］.Technical report.Universität Dortmund， Sonderforschungsbereich 475-Komplexitätsreduktion in Multivariaten Datenstrukturen， Dortmund.

Joyce R J， Janowiak J E， Arkin P A， et al， 2004.CMORPH： A method that produces global precipitation estimates from passive microwave and infrared data at high spatial and temporal resolution ［J］.Journal of Hydrometeorology， 5（3）： 487-503.DOI： 10. 1175/1525-7541（2004）005<0487： CAMTPG>2.0.CO； 2 .

Kavetski D， Kuczera G， Franks S W， 2006.Bayesian analysis of input uncertainty in hydrological modeling： 2.Application［J］.Water Resources Research， 42（W03）： 1-10.DOI： 10.1029/2005WR004368 .

Kuok S C， Yuen K V， 2020.Broad learning for nonparametric spatial modeling with application to seismic attenuation［J］.Computer‐Aided Civil and Infrastructure Engineering， 35（3）： 203-218.DOI： 10.1111/mice.12494 .

Liu Z， Di Z， Qin P， et al， 2022.Evaluation of six satellite precipitation products over the Chinese Mainland［J］.Remote Sensing， 14（24）： 6277.DOI： 10.3390/rs14246277 .

Ma Y Z， Hong Y， Chen Y， et al， 2018.Performance of optimally merged multisatellite precipitation products using the dynamic Bayesian model averaging scheme over the Tibetan Plateau［J］.Journal of Geophysical Research： Atmospheres， 123（2）， 814-834.DOI： 10.1002/2017JD026648 .

Moré J J， 1978.The Levenberg-Marquardt algorithm： Implementation and theory［M］.Springer， Berlin， Heidelberg.In： Watson， G.A.（eds） Numerical Analysis.Lecture Notes in Mathematics， vol 630.DOI： 10.1007/BFb0067700 .

Shen Y， Xiong A Y， Wang Y， et al， 2010.Performance of high‐resolution satellite precipitation products over China［J］.Journal of Geophysical Research： Atmospheres， 115（D02）： 1-17.DOI： 10. 1029/2009JD012097 .

Sunilkumar K T， Narayana Rao T， Satheeshkumar S， 2016.Assessment of small-scale variability of rainfall and multi-satellite precipitation estimates using measurements from a dense rain gauge network in Southeast India ［J］.Hydrology and Earth System Sciences， 20（5）： 1719-1735.DOI： 10.5194/hess-20-1719-2016 .

Tang G Q， Clark M P， Papalexiou S M， et al， 2020.Have satellite precipitation products improved over last two decades？A comprehensive comparison of GPM IMERG with nine satellite and reanalysis datasets［J］.Remote Sensing of Environment， 240： 111697.DOI： 10.1016/j.rse.2020.111697 .

Tang G Q， Ma Y Z， Long D， et al， 2016.Evaluation of GPM Day-1 IMERG and TMPA Version-7 legacy products over Mainland China at multiple spatiotemporal scales［J］.Journal of Hydrology， 533： 152-167.DOI： 10.1016/j.jhydrol.2015.12.008 .

Ushio T， Sasashige K， Kubota T， et al， 2009.A Kalman filter approach to the Global Satellite Mapping of Precipitation （GSMaP） from combined passive microwave and infrared radiometric data ［J］.Journal of the Meteorological Society of Japan.Series II， 87： 137-151.DOI： 10.2151/jmsj.87A.137 .

Wang Y H， Chen J S， Yang D W， 2019.Bayesian assimilation of multiscale precipitation data and sparse ground gauge observations in mountainous areas［J］.Journal of Hydrometeorology， 20（8）： 1473-1494.DOI： 10.1175/JHM-D-18-0218.1 .

Wang Y， Wang L， Li X， et al， 2020.An integration of gauge， satellite， and reanalysis precipitation datasets for the largest river basin of the Tibetan Plateau［J］.Earth System Science Data， 12（3）： 1789-1803.DOI： 10.5194/essd-12-1789-2020 .

Wu H C， Yang Q L， Liu J M， et al， 2020.A spatiotemporal deep fusion model for merging satellite and gauge precipitation in China ［J］.Journal of Hydrology， 584： 124664.DOI： 10.1016/j.jhydrol.2020.124664 .

Xie P P， Xiong A Y， 2011.A conceptual model for constructing high-resolution gauge-satellite merged precipitation analyses［J］.Journal of Geophysical Research， 116（D2）： 1-14.DOI： 10.1029/2011JD016118 .

Xu G Y， Wang Z J， Xia T， 2019.Mapping areal precipitation with fusion data by ANN machine learning in sparse gauged region ［J］.Applied Sciences， 9（11）： 2294.DOI： 10.3390/app9112294 .

Xu R， Tian F Q， Yang L， et al， 2017.Ground validation of GPM IMERG and TRMM 3B42V7 rainfall products over southern Tibetan Plateau based on a high-density rain gauge network［J］.Journal of Geophysical Research： Atmospheres， 122（2）： 910-924.DOI： 10.1002/2016JD025418 .

Yang X H， Han P， Yang Z T， et al， 2022.Broad Learning Framework for Search Space Design in Rayleigh Wave Inversion［J］.IEEE Transactions on Geoscience and Remote Sensing， 60： 1-17.DOI： 10.1109/TGRS.2022.3208616 .

Yan L C， Yoshua B， Geoffrey H， 2015.Deep learning［J］.Nature， 521（7553）： 436-444.DOI： 10.1038/nature14539 .

Zhang T， Liu Z L， Wang X H， et al， 2018.Facial expression recognition via broad learning system［C］.2018 IEEE international conference on systems， man， and cybernetics （SMC）.Japan： Miyazaki， 1898-1902.DOI： 10.1109/SMC.2018.00328 .

Zhao G X， Wang X S， Kong Y， et al， 2021.Spectral-spatial Joint classification of hyperspectral image based on broad learning system ［J］.Remote Sensing， 13（4）： 583.DOI： 10.3390/rs13040583 .

Zhao H M， Zheng J J， Xu J J， et al， 2019.Fault diagnosis method based on principal component analysis and broad learning system ［J］.IEEE Access， 7： 99263-99272.DOI： 10.1109/ACCESS. 2019.2929094 .

Zhou Y Y， Li X， Tang Q H， et al， 2022.An assimilating model using broad learning system for incorporating multi-source precipitation data with environmental factors over southeast China ［J］.Earth and Space Science， 9： e2021EA002043.DOI： 10.1029/2021EA002043 .

Zhou Y， Qin N X， Tang Q H， et al， 2021.Assimilation of multi-source precipitation data over southeast China using a nonparametric framework［J］.Remote Sensing， 13（6）： 1057.DOI： 10. 3390/rs13061057 .

胡庆芳， 2013.基于多源信息的降水空间估计及其水文应用研究［D］.北京： 清华大学， 1-123.

Hu Q F， 2013.Rainfall spatial estimation using multi-source information and its hydrological application［D］.Beijing： Tsinghua University， 1-123.

黄慧君， 郑建萌， 马涛， 等， 2023.夏季高原低涡切变影响下云南大雨暴雨的分布及成因研究［J］.高原气象， 42（2）： 403-416.DOI： 10.7522/j.issn.1000-0534.2021.00114.Huang H J ，

Zheng J M， Ma T， et al， 2023.Distribution and genesis of heavy rain over Yunnan affected by the plateau low vortex shear in summer［J］.Plateau Meteorology， 42（2）： 403-416.DOI： 10.7522/j.issn.1000-0534.2021.00114 .

贾何佳， 李谢辉， 王磊， 等， 2022.基于机器学习的西南地区遥感干旱监测与评估［J］.高原气象， 41（6）： 1572-1582.DOI： 10.7522/j.issn.1000-0534.2022.00006.Jia H J ，

Li X H， Wang L， et al， 2022.Remote sensing drought monitoring and assessment in southwestern China based on machine learning［J］.Plateau Meteorology， 41（6）： 1572-1582.DOI： 10.7522/j.issn. 1000-0534.2022.00006 .

李哲， 2015.多源降雨观测与融合及其在长江流域的水文应用［D］北京： 清华大学， 1-140.Li Z， 2015.Multi-source precipitation observations and fusion for hydrological applications in the Yangtze River Basin［D］.Beijing： Tsinghua University， 1-140.

刘元波， 傅巧妮， 宋平， 等， 2011.卫星遥感反演降水研究综述［J］.地球科学进展， 26（11）： 1162-1172.DOI： 10.11867/j.issn. 1001-8166.2011.11.1162.Liu Y B ，

Fu Q N， Song P， et al， 2011.Satellite retrieval of precipitation： An overview［J］.Advances in Earth Science， 26（11）： 1162-1172.DOI： 10.11867/j.issn.1001-8166.2011.11.1162 .

肖贻青， 娄盼星， 李明娟， 等， 2023.西北涡与西南涡共同作用引发秦巴区域大暴雨的成因分析［J］.高原气象， 42（1）： 98-107.DOI： 10.7522/j.issn.1000-0534.2022.00013.Xiao Y Q ，

Lou P X， Li M J， et al， 2023.Analysis on a heavy rainstorm in Qinba Region caused by Southwest Vortex and Northwest Vortex［J］.Plateau Meteorology， 42（1）： 98-107.DOI： 10.7522/j.issn. 1000-0534.2022.00013 .

晏红明， 王灵， 金燕， 等， 2023.云南冬季气温变化的主要模态及其影响的关键环流因子［J］.高原气象， 42（2）： 386-402.DOI： 10.7522/j.issn.1000-0534.2021.00070.Yan H M ，

Wang L， Jin Y， et al， 2023.Dominant patterns of winter temperature variation in Yunnan and key circulation factors affecting on them［J］.Plateau Meteorology， 42（2）： 386-402.DOI： 10.7522/j.issn. 1000-0534.2021.00070 .

尹雄锐， 夏军， 张翔， 等， 2006.水文模拟与预测中的不确定性研究现状与展望［J］.水力发电， 32（10）： 27-31.

Yin X R， Xia J， Zhang X， et al， 2006.Recent progress and prospect of the study on uncertainties in hydrological modelling and forecasting［J］.Water Power， 32（10）： 27-31.

Options
文章导航

/

〈 〉

本系统由北京玛格泰克科技发展有限公司设计开发 技术支持：support@magtech.com.cn