1 引言
2 基于集合变换卡尔曼滤波和混合同化的对流尺度集合预报方法
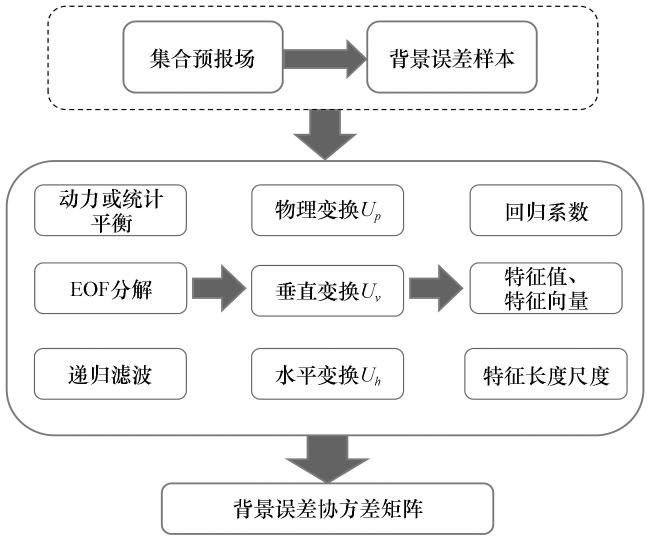
3 多元变量背景误差协方差计算方法
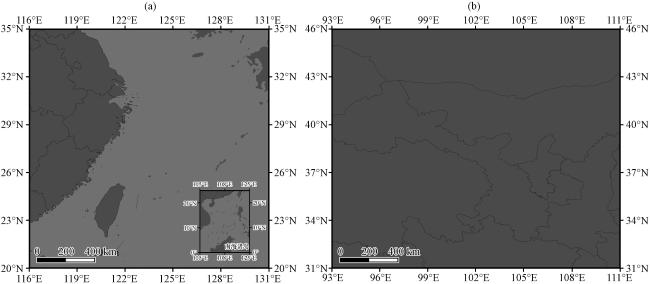
4 试验方案介绍
5 台风和高原边坡对流个例
5.1 2022年台风“梅花”概况
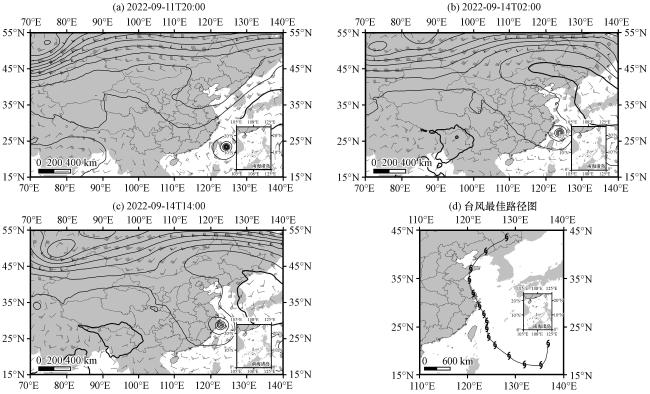
图3 各时次500 hPa位势高度(黑实线, 单位: dagpm, 加粗黑实线为588 dagpm等高线)和风场(风羽, 单位: m·s-1)分布(a) 2022年9月11日20:00, (b) 2022年9月14日02:00, (c) 2022年9月14日14:00, (d) 台风最佳路径图Fig.3 Geopotential height (solid black line, Unit: dagpm, bold solid black line is 588 dagpm contour line) and wind (barb, unit: m·s-1) of 500 hPa at various times.(a) 20:00 on 11 September 2022, (b) 02:00 on 14 September 2022, (c) 14:00 on 14 September 2022, (d) the best track of the typhoon |
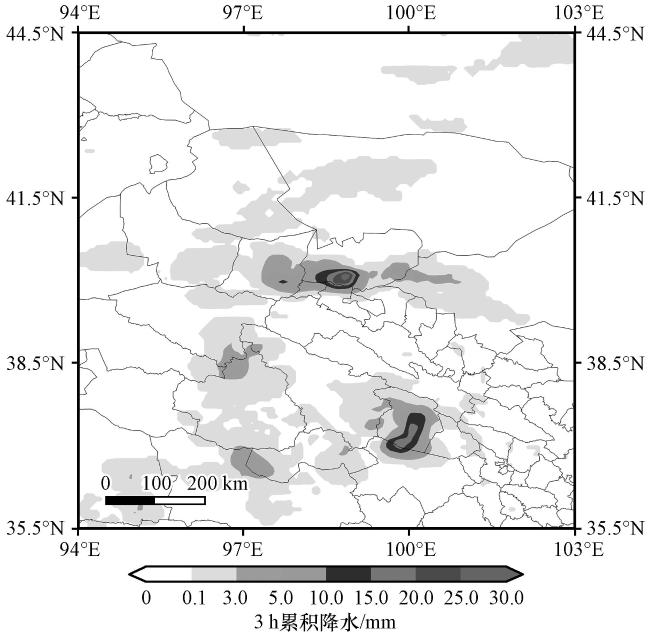
5.2 2022年一次高原边坡对流概述
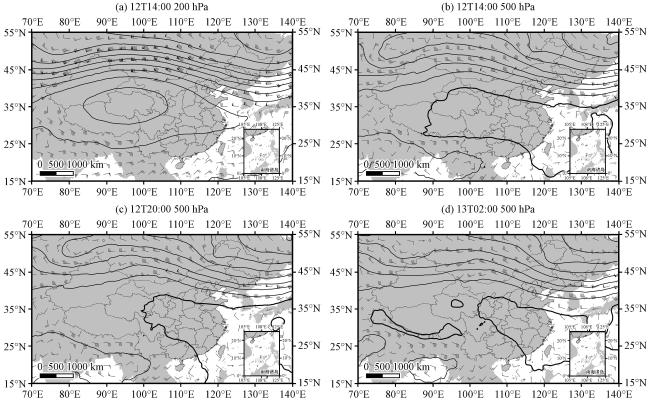
图5 2022年8月12 -13日各时次位势高度(黑实线, 单位: dagpm)和风场(风羽, 单位: m·s-1)分布(a) 12T14:00 200 hPa, (b) 12T14:00 500 hPa, (c) 12T20:00 500 hPa, (d) 13T02:00 500 hPaFig.5 Geopotential height (solid black line, unit: dagpm, bold solid black line is 588 dagpm contour line) and wind (barb, unit: m·s-1) at various times from 12 to 13 August 2022.(a) 14:00 on August 12, 200 hPa; (b) 14:00 on August 12, 500 hPa; (c) 20:00 on August 12, 500 hPa; (d) 02:00 on August 13, 500 hPa |