高原气象

高原气象 >

2025 , Vol. 44 >Issue 3: 733 - 746

DOI: https://doi.org/10.7522/j.issn.1000-0534.2024.00084

一个基于潜在影响的降水预报评分方法

  • 潘留杰 , 1, 2 ,
  • 张宏芳 , 2, 3 ,
  • 祁春娟 1, 2 ,
  • 卢珊 2, 3 ,
  • 杜丽莉 1, 2
展开
  • 1. 陕西省气象台，陕西 西安 710014
  • 2. 秦岭和黄土高原生态气象环境重点实验室，陕西 西安 710014
  • 3. 陕西省气象服务中心，陕西 西安 710014
张宏芳（1981 -）， 女， 陕西平利人， 正高级工程师， 主要从事应用气象与研究. E-mail：

潘留杰（1978 -）， 男， 陕西石泉人， 正高级工程师， 主要从事天气预报与研究. E-mail：

收稿日期: 2024-01-10

  修回日期: 2024-07-26

  网络出版日期: 2025-04-29

基金资助

中国气象局气象能力提升联合专项重点项目(24NLTSZ003)

陕西省社会发展关键领域项目(2022SF-360)

中国气象局创新发展专项(CXFZ2022J023)

陕西省自然科学基础研究计划项目(2023-JC-QN-0285)

收起

A Precipitation Forecast Score Based on Potential Impact

  • Liujie PAN , 1, 2 ,
  • Hongfang ZHANG , 2, 3 ,
  • Chunjuan QI 1, 2 ,
  • Shan LU 2, 3 ,
  • Lili DU 1, 2
Expand
  • 1. Shaanxi Meteorological Observatory，Xi'an 710014，Shannxi，China
  • 2. Key Laboratory of Eco-Environment and Meteorology for the Qinling Mountains and Loess Plateau，Xi'an 710014，Shannxi，China
  • 3. Shaanxi Meteorological Service Centre，Xi'an 710014，Shannxi，China

Received date: 2024-01-10

  Revised date: 2024-07-26

  Online published: 2025-04-29

Copyright

© Editorial Department of Plateau Meteorology （CC BY-NC-ND）
Fold

摘要

传统的二分法列联表检验在计算降水TS（Threat Score）评分时， 漏报和空报事件具有相同的权重， 满足阈值条件的不同降水量的漏报事件的权重相同， 同时阈值区间内不同降水量的命中事件也具有同等的频次计算方式， 在高分辨率网格降水预报检验中显得不够精细。事实上， 同为命中但数值不同， 或漏报事件中预报和观测降水量差异程度的大小产生的影响可能完全不同。本文在综合考虑降水命中、 漏报次数和降水量的基础上， 提出了降水影响预报评分ITS （Impact Threat Score）。“影响”定义为因预报命中或漏报降水对实际发生降水可能带来的潜在后果的刻画。对于命中和漏报事件， 分别通过观测降水的对数以及观测与预报降水的差值的对数定义影响因子， 在此基础上累计得到时空尺度上事件的等价影响AI和CI。单纯考虑CI的影响评分ITS0， 定义为ITS的一个子项； 综合考虑AI和CI共同作用的降水评分定义为ITS。分析表明： ITS0根据漏报降水的差异程度， 赋予动态权重， 能够清楚地分辨漏报事件的影响程度； 而ITS对命中大量级降水有奖赏， 当命中的降水数值越大， 漏报降水的数值与观测差异越小， ITS越大， 对真实降水产生潜在后果的刻画能力也越好。实际应用中， 采用ITS0还是ITS， 可以根据评价的目的和需求来综合考虑。

关键词： 预报检验; 降水影响; TS评分; ITS0评分; ITS评分

本文引用格式

潘留杰 , 张宏芳 , 祁春娟 , 卢珊 , 杜丽莉 . 一个基于潜在影响的降水预报评分方法[J]. 高原气象, 2025 , 44(3) : 733 -746 . DOI: 10.7522/j.issn.1000-0534.2024.00084

Abstract

In traditional contingency tables， the hit and false alarm events are given equal weights when calculating the precipitation TS score.The weight of missed precipitation events with different amounts that satisfy the threshold conditions is also the same.At the same time， the frequency calculation method for hit events of different precipitation amounts within the threshold range is also the same.However， these methods lack precision in the verification of high-resolution grid precipitation forecasts.In fact， the impact of differences in observed precipitation values， even when predictions hit the threshold， may be completely different.Additionally， the impact of differences in the forecasting and observation of precipitation values in missed precipitation events may also vary greatly.The article proposes a precipitation impact forecast score based on the comprehensive consideration of precipitation hit rate， missed alarm ratio， and precipitation amount."Impact" is defined as the characterization of potential consequences that may result from forecast hits or misses on actual precipitation occurrences.For hit and missed events， impact factors are defined by taking the logarithm of observed precipitation and the logarithm of the difference between observed and forecasted precipitation.Based on this， equivalent impacts （AI and CI） of hit and missed events are accumulated at the spatiotemporal scale.The scoring solely considering the impact of CI is defined as a sub-item of the Impact Threat Scoring （ITS）.The precipitation scoring that takes into account the combined effects of A I and CI is defined as the ITS score.Analysis shows that ITS0 assigns dynamic weights based on the degree of difference in missed precipitation， allowing for a clear distinction of the impact level of missed events.On the other hand， ITS rewards the accurate prediction of heavy precipitation.The larger the hit precipitation values and the smaller the difference between the forecasted and observed values in missed events， the larger the ITS score.These factors result in a better ability to depict the potential consequences on actual precipitation.

Key words： forecast verification; precipitation impact; TS score; ITS0; ITS score

1 引言

降水是天气预报中最为重要的气象要素之一， 这不仅是因为降水直接与人们的生活生产紧密相关， 而且降水异常往往造成严重的气象灾害， 对人类生命安全、 生态环境带来严重的影响（Jones et al， 2004； 毕宝贵等， 2016； 代刊等， 2018）。在全球变暖背景下， 极端降水事件的频率和强度呈显著上升的趋势（Alexander et al， 2006； 董晓云等， 2020）。重大极端降水事件频发， 2021年7月18 - 21日， 中国河南遭遇了历史上罕见的极端暴雨（梁旭东等， 2022）， 河南郑州的单日降水量为624.1 mm； 2012年7月12日北京24 h平均降雨量为170.0 mm， 单站最大雨量超过460.0 mm； 2023年7月29日至8月2日， 受台风水汽输送、 副热带高压和地形作用共同影响， 中国北京市及周边地区出现灾害性特大暴雨天气， 气象观测站记录最大小时降水强度达到111.8 mm。这些极端降水事件造成了巨大的影响和严重人员伤亡以及经济财产损失。因此， 深化极端天气气候事件特别是降水的研究， 对提高预报预警能力越来越重要， 其研究工作也越来越广泛（徐珺等， 2022； 郭大梅等， 2022； 江洁等， 2022； 张夕迪等， 2023； 刘侃等， 2024）。
降水预报能力的客观评价是气象预报科研业务中的重要课题（Schaefer， 1990； Baldwin and Kain， 2006； Brill and Mesinger， 2009； 张宏芳等， 2014； 肖颖等， 2023； 谢泽明等， 2024； 刘雨萌等， 2025）。为了准确评价降水的预报表现， 基于二分法列联表， 在点对点对比的基础上定义诸如命中率（POD）、 空报率（FAR）、 预报偏差（Bias）、 TS评分等一系列评分指数来判别模式的预报表现（Mason， 2004； Ebert et al， 2013）， 在天气预报检验中有着广泛的应用， 其中， TS评分也被称作临界成功指数CSI（Critical Success Index）， 是降水预报检验中最重要的指标之一。二分法列联表检验最早被Finley（1884）应用于龙卷的预报效果评估， 至今已经有一百多年的历史。针对Finley（1884）的检验工作， Gillbert （1884）注意到因为检验中包含大量的预报无龙卷， 事实也未观测到龙卷事件发生的样本， 采用准确率不能反映真实的预报能力， 并建议在检验中不考虑“正确预报未发生事件的样本”， 进而定义了CSI检验公式。随后降水检验中也发现存在类似情况， 未预报降水也没有观测到降水的事件样本在降水检验中占比非常大， 客观反映降水预报能力应该去除这类样本， 因此定义了威胁评分TS。
近几十年来， 气象观测手段和天气预报能力快速发展。一方面， 地面气象观测站点更加稠密， 卫星、 雷达等遥感探测设备还能够在空间上作为地面气象观测站点的有效补充， 进而可以观测到更加局地的降水信息； 另一方面， 数值天气预报NWP （Numerical Weather Forecast ）的水平网格间距越来越小， 模式中的积云参数化方案逐渐被能够更加精细描述小尺度大气动力框架的“允许对流”CAM （Convection Allowing Model） 模型所替代， 能更清楚地表达四维空间中天气要素的中小尺度信息， 提供更多的预报细节； 但CAM模型对中小尺度天气结构的不精确描述， 细小的相位误差可能导致空间上高可变性的要素预报出现更大的强度、 形态等预报误差。有研究表明（Mass et al， 2002）， 高分辨率模式通常比粗分辨率NWP的RMSE（Root Mean Squared Error） 更大， 即使是相对平滑的高空风场或温度场。这是因为就RMSE的定义来说， 相对平滑的要素场对减小RMSE更有利， 而更高的水平分辨率必然意味着包括了更多的细节和局地预报信息。这些细节或局地预报信息可能不正确， 在这种情况下， 细节信息就转化为噪音。
为了增强高分辨率NWP的预报检验能力， 气象工作者发展了一系列空间检验方法（Gilleland et al， 2009； Ahijevych et al， 2009； Ebert， 2010； Gilleland et al， 2010； 张宏芳等， 2021； Wu et al， 2020； 潘留杰等， 2024a， 2024b）。宏观来看空间检验主要包括： 属性判别法、 形变场法、 邻域法、 尺度分离法四类。这些检验方法放宽了预报和观测的匹配条件限制， 检验结果与预报员的主观判断更加吻合， 广泛应用于NWP预报性能的诊断分析（Mason， 1989； Brill and Mesinger， 2009； 刘静等， 2022）。但是， 空间检验受阈值条件、 参数设定、 个性需求等因素影响， 其适用性需要多视角分析， 与其相比， 传统二分法“点对点”检验的匹配精度更有优势（薛春芳和潘留杰， 2016； 潘留杰等， 2023）。目前， 天气预报业务中， 二分法检验评分仍然是最为重要的评价指标， 不足之处在于没有考虑不同降水量数值的影响， 特别是就TS评分计算来说， 空报和漏报具有相同的地位， 事实上， 强降水的漏报往往造成严重的灾害事故。本文在传统二分法检验TS评分的基础上， 提出了基于影响的降水预报评分ITS （Impact Threat Score）， 以期为降水二分法检验提供更加丰富的判别标准。

2 传统二分法预报评分

2.1　二分法TS评分

按照是否满足给定的阈值， 可以对降水事件进行“0” “1”标记。对于预报和观测降水来说， 可以有4种组合（表1）， 即： A同时满足阈值条件； B预报满足阈值条件， 观测不满足； C预报不满足阈值条件， 观测满足； D预报和观测同时不满足阈值条件。对关注范围内的所有站点或格点统计计算， 进而定义预报评分。通常， A和B分别被称为命中和空报的次数， C为漏报的次数， D为正确预报未出现的次数。
表1 二分类列联表

Table 1 The binary classification contingency table

观测发生 观测未发生
预报事件发生 A B
预报事件未发生 C D
根据事件分类， 常用的评分指数命中率POD、 空报率FAR、 漏报率MAR（Sprenger et al， 2017）、 Bias和TS评分的定义如下：
P O D = A A + C
F A R = B A + B
M A R = C A + C
T S = A A + B + C
B i a s = A + B A + C
从评分定义的公式可以看出， TS仅受A、 B和C的影响， 与D无关。TS表达式可以变换为：
T S = [ ( P O D ) - 1 + ( 1 - F A R ) - 1 - 1 ] - 1
公式（6）表明， TS评分与命中率POD和空报率FAR有高度的非线性依赖。

2.2　灾害性天气评价中TS评分的局限

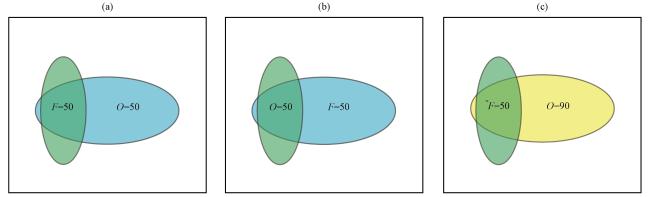
Mason（1989）分析发现， TS评分与事件发生频率紧密相关。为了克服不同气候背景下随机偶然预报正确事件的影响， 发展了ETS （Equitable Threat Score）评分（Brill and Mesinger， 2009）， 也被称作GSS（Gilbert Skill Score）评分 。事实上， 除去随机事件的影响之外， 在降水检验中， 计算TS评分时还存在两种情况需要斟酌： 一是B和C具有相同的地位， 但对不同量级的降水检验而言， 其重要性完全不同， 譬如对气象灾害防御而言， 漏报强降水可能造成严重的损失， 而对于微量降水， 漏报无关紧要。二是对于A而言， 超过单向检验阈值的事件计算相同的次数， 但阈值之上不同强度的降水事件带来的影响， 可能完全不同， 这种情况即使在双向限定阈值评分中也大量存在。图1给出了三种情景的示例， 三种场景下暴雨的TS评分完全一致， 但与图1（a）相比， 图1（b）漏报更少。图1（c）和图1（a）具有完全相同的落区和降水量级， 但图1（c）中， 命中区域的实际降水可能产生更严重的后果， 仍然差别巨大， 在这种情景下， TS评分无法反映在哪种情形下， 预报降水能够更好地表达真实降水可能带来的潜在影响。
图1 不同的预报和观测降水场情景示例（a）观测降水面积大于预报面积， （b）预报降水面积大于观测面积， （c）观测降水面积大于预报面积， 同时降水量大于预报降水量。“F”表示预报， “O”表示观测， 数值表示降水的量级

Fig.1 Illustrates examples of different scenarios for forecasted and observed precipitation fields.（a） The observed precipitation area is larger than the forecasted area.（b） The forecasted precipitation area is larger than the observed area.（c） The observed precipitation area is larger than the forecasted area， and the precipitation amount is also greater than the forecasted precipitation amount.The letter "F" represents the forecast， the letter "O" represents the observation， and the numerical values indicate the amount of precipitation

3 ITS评分定义

大量级降水事件漏报可能会导致严重的气象灾害， 是否漏报以及超过阈值命中事件的降水数值的大小， 都是判断实际降水可能产生影响的重要因素。因此， 首先定义影响因子， 进而定义基于影响的降水预报ITS评分。一般来说， 量级较低的降水造成的气象灾害较小， 量级越大， 可能造成的气象灾害越严重。基于这些原因， 在评分中不仅需要关注不同事件发生的次数， 而且需要加入降水量数值的影响， 可能更能表现预报降水对实际观测降水可能带来的影响。需要重点明确的是， 降水影响含义并不是因降水而导致的直接后果， 而是因预报命中或漏报降水对实际发生降水可能带来的潜在后果的刻画。如何加入降水量级的影响， 最重要的是构建降水量级与发生次数的关系。对于命中降水来说， 不同量级的降水应该有不同的权重； 对于漏报降水来说， 应该有所惩罚， 即使是非常小的降水漏报， 相对于正确的降水预报需要区分对待， 其权重也应该不同。结合预报经验和对数性质， 影响因子主要采用以下原则： ①影响因子应该对所有量级降水适用； ②锚定一个降水量， 其对应的影响因子为1； ③锚定数值之外的降水量， 其影响因子是锚定降水量影响因子的倍乘， 倍乘系数对于超过锚定数值的降水量来说， 应该大于1， 低于锚定数值来说， 应该小于1， 但不是线性关系。按照设定原则， 提出采用降水量的对数作为影响因子的转换函数， 锚定1.0 mm降水的影响因子为1。
表2给出了命中和漏报降水影响因子的详细定义。如果仅有一次命中和一次漏报， 单个事件的影响因子分别定义为 1 + l g O和 1 + l g ( O - F )， 这里O表示观测降水量， F表示预报降水量。检验整个时空要素场时， 对每一单个事件的影响因子求和， 定义为等价影响。从表2可以看出， 对于命中和漏报降水事件来说， 影响因子的关注点是不同的， 命中事件A重点考虑了降水量， 即降水量越大， 影响因子越大。对漏报事件C来说， 则主要聚焦于观测与预报降水的差值， 两者差值越大， 影响因子越大。
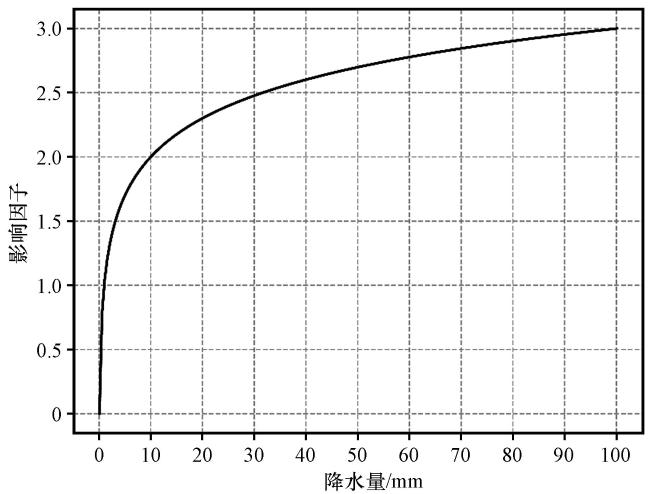
表2 降水事件影响因子（A， C=1）及等价影响

Table 2 The impact factors of precipitation events （A， C=1） and their equivalent impact

观测 预报 事件 影响因子 等价影响
O F A 1 + l g O A I = ∑ A × ( 1 + l g O )
C 1 + l g ( O - F ) C I = ∑ C × [ 1 + l g ( O - F ) ]

O表示观测， F表示预报（"O" in the table represents observation， while "F" represents forecast）

设定R表示降水量， 以24 h累计降水检验为例。图2给出了降水影响因子的变化曲线， 对命中来说， R为1.0 mm， 影响因子为1， 当R低于1.0 mm， 随着R的减小， 影响因子随之减小， R为0.1 mm时， 影响因子为0； 当R增大到10.0 mm时， 影响因子为2， 增大到100.0 mm时， 影响因子为3， 随之类似。分析认为， 影响因子的这种分布是比较合理的， 1.0 mm以下的降水对工农业生产的影响逐渐减小， 而对准确的大量级降水预报的评分赋予更高的权重， 对基于评分优选预报产品， 防汛减灾有重要意义。对漏报事件C来说， O总大于F， 以两者差值作为影响因子的变换函数， 差值越大， C赋予的权重越大， 当差值低于1， C值逐渐减小， 相对单纯地计算超过规定阈值的次数， 也更有意义。事件C的影响因子曲线变化分布与命中事件A一致。
图2 影响因子随降水量 （观测降水O或预报与观测降水的差值O-F） 的变化曲线

Fig.2 Variation curve of impact factor with precipitation amount （observed precipitation O or difference between forecast and observed precipitation O-F）

累计单点事件的影响因子求和， 即构成某一检验区域范围或时间序列降水事件的等价影响， 对于命中事件A和漏报事件C， 其等价影响分别定义为 A I和 C I， 进而定义评分指数 I T S 0和 I T S， 具体如公式（7）和（8）所示。在这里， I T S 0为仅考虑漏报事件的影响， 本文最终定义 I T S同时考虑了漏报和命中事件量级的影响， 但分析认为 I T S 0评分在预报检验中仍然有意义和适用范围， 因此加以保留。
利用 A I和 C I定义 I T S， 也可以在此基础上定义基于 A I和 C I的命中率和空报率， 但基于 A I和 C I定义的命中率和空报率不具有公式（5）的变换关系。
I T S 0 = A A + B + ∑ C × [ 1 + l g ( O - F ) ] = A A + B + C I
I T S = ∑ A × ( 1 + l g O ) ∑ A × ( 1 + l g O ) + B + ∑ C × [ 1 + l g ( O - F ) ] = A I A I + B + C I
以不同量级降水命中、 空报和漏报均为1次为例。对于 I T S 0来说， 假定A， B， CI等于1， I T S 0即蜕化为TS评分。当观测O和预报F的差值在0.1~100.0 mm之间变化时［图3（a）］， 传统的TS评分恒定为0.33， 对降水量不敏感。但 I T S 0最大可以达到0.50， 随着降水差值的增大， I T S 0逐渐减小， 降水量差值达到100.0 mm时， I T S 0减小到0.2。整体而言， I T S 0根据漏报降水的差异程度， 赋予了动态权重， 能够更加精确的刻画实际降水的预报能力。对于 I T S来说［图3（b）］， 观测降水O和两者的差值O-F对评分都有重要影响， 但O对评分的影响是决定性的。当O较小时， 即使观测和预报差异很小， I T S评分依然较小。当两者差值在0.1~100.0 mm之间变化， O为0.5 mm时， I T S值域范围为0.18~0.41； 当O为100.0 mm时， I T S的值域范围0.43~0.75， 因此命中大量级降水对ITS评分的奖赏是非常明显的， 这也反映了评分的目的， 即以降水量为基础及其可能造成影响的预报评分。
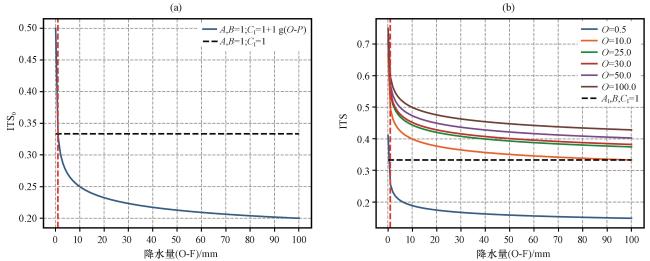
图3 影响评分随降水量差值和降水量的变化曲线（a） ITS0， （b）ITS， 图（a）中黑色虚线为A， B， CI等于1的ITS0评分， 图（b）中的黑色虚线为AI， B， CI等于1的ITS评分， 红色虚线为O-F为1.0 mm或者O为1.0 mm所对应的位置

Fig.3 The curve of impact scores with changes in precipitation difference and precipitation amount.（a） ITS0， （b） ITS.The black dashed lines in （a） and （b） represent the impact scores for A， B， CI equal to 1 and AI， B， CI equal to 1.The red dashed line represents the position corresponding to O-F equals 1.0 mm or O equals 1.0 mm

4 假想个例的降水预报评分试验

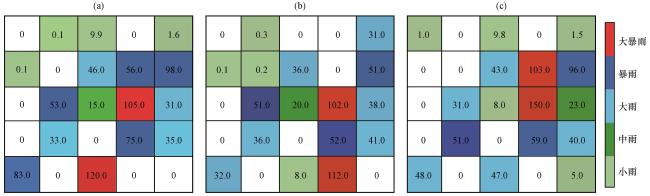
对于传统TS评分来说， 为了刻画不同大小降水量的影响， 采用降水量分级的方法来解决这一问题， 但分级区间不可能过小， 评分一般与日常天气预报中的降水等级一致。然而ITS和ITS0在分辨事件发生频次影响的同时， 根据降水量的大小， 为对应频次赋予不同的影响权重， 不仅适用于分级降水预报的评价， 而且对于整个降水场变量来说， 也有很好的适用性。图4给出了假想的观测和两个假想的降水个例预报， 来进一步分析ITS或ITS0的评分特点。为了方便表述， 给图4每个子图格点赋予坐标， 左下角为起始坐标值， 惯常 x向东和 y向北方向逐渐递增， 譬如图4（a）中左下角为 a 0,0， y方向增加1的格点标注为 a 1,0， x方向增加1个格点标注为 a 0,1， 以此类推， 图4（b）、 4（c）和图4（a）类似。
图4 假想的降水个例（a）观测降水， （b）假想的预报个例1， （c）假想的预报个例2， 图中数值为降水量（单位： mm）

Fig.4 Hypothetical precipitation cases.（a） Observed precipitation， （b） Hypothetical precipitation forecast case 1， （c） Hypothetical precipitation forecast case 2.The numbers in the figure represent precipitation amounts （unit： mm）

单向阈值小雨 R≥0.1 mm和暴雨 R≥50.0 mm降水， 假想预报个例1和个例2的事件分类完全相同（表3）， 两者的TS评分也完全一致［图5（a）］。但由于命中点的降水量级的差异， 个例1和个例2的命中事件等价影响显著不同。对于小雨的预报， 由于 a 4,1格点降水为0.1 mm， 虽然 c 4,1出现漏报， 但其影响因子为0， 累计所有格点的影响因子， 个例2的等价影响CI最终为0， 预报2的ITS0和ITS评分显著高于预报个例1。对于暴雨来说， 两个个例的传统TS评分也完全一致， 但对AI来说， 个例2命中的 a 3,3高于个例1命中的 a 2,1。对于 a 0,0， 虽然个例1和个例2同时表现为漏报， 但个例2降水预报与观测的差异较小， 导致个例2的AI略偏大， CI略偏小， 个例2的暴雨ITS0和ITS优于个例1。结果也充分体现了评分能够更好地表现不同情景下降水量的预报能力。
表3 单向累加的降水量分级的降水预报事件分类

Table 3 Classification of precipitation forecast events based on one-way accumulated precipitation amount

TS ITS0或ITS
预报1事件 预报2事件 预报1事件 预报2事件
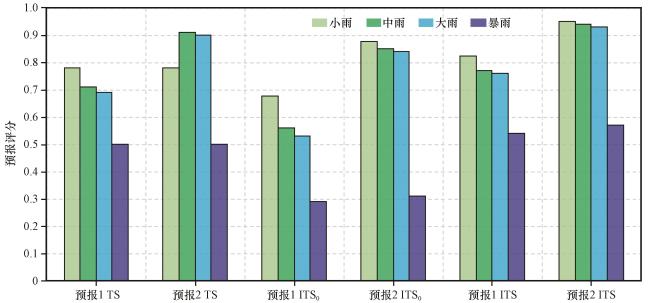
小雨（R≥0.1 mm） A=14 B=2 A=14 B=2 AI=31.21 AI =35.95
C=2 D=7 C=2 D=7 CI=4.7 CI =0.0
中雨（R≥10.0 mm） A=10 B=2 A=12 B=1 AI =26.9 AI =32
C=2 D=11 C=0 D=13 CI =5.7 CI =0.0
大雨（R≥30.0 mm） A=9 B=2 A=10 B=1 AI =24.75 AI =28.1
C=2 D=12 C=1 D=13 CI =5.8 CI =1.9
暴雨（R≥50.0 mm） A=4 B=1 A=4 B=1 AI =11.61 AI =11.64
C=3 D=17 C=3 D=17 CI =8.5 CI =7.7
图5 假想个例的不同量级降水预报的TS、 ITS0和ITS评分

Fig.5 TS， ITS0， and ITS scores for different categories of precipitation forecasts in hypothetical cases

个例2和个例1的小雨和暴雨TS评分相同， 但中雨和大雨TS评分存在显著差异， 这种差异的结果在R≥0.1 mm降水的ITS0和ITS能够清楚体现出来。事实上， 通过阈值的细分， 不同阈值区间的TS评分的整体表现结果和ITS0、 ITS是一致的。但在实际业务中， 阈值无限细分是很难做到的。而ITS0和ITS的优点在于避免用一个评分在阈值无限细分的情况下， 全面反映降水预报在频次、 量级等方面的综合性能。

5 预报评分应用

为了进一步分析ITS评分的特性， 以国家气象信息中心的雷达、 卫星和地面观测站的三源融合网格降水分析实况CMPAS （CMA Multi-source Merged Precipitation Analysis System ）为参照， 采用POD、 MAR、 TS、 ITS0和ITS评分， 分析2022年ECMWF （European Centre for Medium-Range Weather Forecasts ） 模式降水量R≥50.0 mm的单向阈值暴雨在中国的预报表现， 文中涉及的地图是基于自然资源部标准地图服务网站下载的审图号为GS（2016）1569 号的中国地图制作， 底图无修改。有研究表明（潘旸等， 2018）， CMPAS基于概率密度函数匹配法订正雷达和卫星估测降水产品的系统偏差， 在其基础上采用贝叶斯模型平均方法融合地面站点降水观测、 雷达和卫星反演降水数据研制而成。CMPAS与站点观测平均误差为-0.0026 mm·h-1， 独立检验RMSE为0.730 mm·h-1， 相关系数为0.786， 产品精准度高， 可以用来评估模式的降水预报性能。ECMWF数据为每日12:00（世界时， 下同）下发的降水预报产品。需要说明的是， ECMWF降水预报分辨率为0.125°×0.125°， 时间分辨率为3 h。考虑到实际预报业务中模式资料的可用性， 将ECMWF降水预报资料统一截断12 h， 处理成与观测资料时效对应的24 h累计降水。此处重点分析预报评分在前24 h降水预报中的特性， 即分析时段为模式起报后12~36 h的降水量。CMPAS资料时间分辨率为逐小时， 空间分辨率为0.05°×0.05°（以下简称CMPAS05）。为了方便对比， 将ECMWF模式资料插值成与CMPAS05一致的空间分辨率。
针对ITS0和ITS的实际降水应用， 重点分析R≥0.1 mm和R≥50.0 mm的两种代表性类型， 即晴雨和暴雨及以上量级降水预报的特征表现。以≥0.1 mm的降水预报为阈值， 主要目的是分析ITS0和ITS在所有降水量级中的适用性， 而超过50.0 mm的降水， 可能会对工农业生产带来较大的影响。图6给出了2022年中国区域R≥0.1 mm降水统计结果的空间分布。从R≥0.1 mm的发生次数［图6（a）］来看， 西南、 华南和东北地区降水的发生次数高， 在四川盆地、 云南西部最大超过220次， 这些地区的漏报率普遍在10%以下。同时， 新疆和内蒙古等地的降水发生次数较低， 但模式漏报率却相对明显。小雨量级降水预报频次偏多是ECMWF模式的显著特点（张宏芳等， 2014）。由于在ITS0评分中， 漏报次数C及漏报与观测降水数值的差异程度是最主要的因素， 对R≥0.1 mm的降水来说， 发生次数高的华南地区漏报率低， 而漏报率较高的中国北方， 降水发生次数较少， 导致绝对漏报次数较低， 因此ITS0（图略）整体和TS评分［图6（c）］ 基本一致。相对TS， ITS评分在全国大部分地区都是增加的［图6（d）］， 平均增加0.048， 特别是在西北地区东部、 华中地区增加明显。从公式（8）来看， 因为C较小， 导致CI不是主要影响因子， ITS增大主要受AI的影响， 降水量大的地区， AI较大， 从而空报次数B在ITS评分分母中权重减小。而在华北、 内蒙古一些地区， ITS减小， 主要原因是在北方地区的降水量较小， 一些情况降水量小于1.0 mm， 增大了B和CI在ITS中权重。
图6 2022年中国区域降水量R≥0.1 mm的预报检验（a）发生次数， （b）漏报率MAR， （c）TS评分， （d） ITS评分

Fig.6 Verification of ECMWF model forecast for precipitation R≥0.1 mm in China for the year 2022.（a） the number of occurrences， （b） MAR， （c） TS score， （d） ITS score

图7给出了超过50.0 mm降水的发生次数、 MAR、 POD和TS评分的空间分布。从图7中可以看出， 暴雨发生次数具有典型的地域特征， 东南部次数高， 西北部显著偏低， 广东、 海南单点次数最多超过20次， 西北部内陆很多地方年均发生不到1次。从MAR来看， 华南沿海、 西南地区漏报率高， 部分地方超过0.45， 而山东、 辽宁、 江西漏报率低。从FAR来看（图略）， 东南沿海空报率明显低于华中、 华北和东北一些地区， 在河南、 陕西、 山西和吉林、 黑龙江部分地方FAR接近或达到1.0， 可能的原因一方面是由于模式在不同区域的预报性能差异； 另一方面， 这些地区本身暴雨次数少， 尽管空报次数绝对数值并不高， 但空报率却非常大。POD和FAR在空间位置上有明显的互斥关系， FAR高值区一般为POD的低值区， 但在华南和东南沿海， 一些区域FAR较低， 但POD也并不高， 这可能是这些地区暴雨实际发生的频次较高， 暴雨漏报可能导致较低的命中率。华北、 东北和西北地区东部TS评分高值区能很好地反映其与POD的对应关系， 在陕西南部、 山西北部、 山东、 辽宁等地命中率高值区与TS评分大值区非常吻合， 数值上超过0.9， 是年暴雨发生次数少， 且命中的直接体现， 而在东南沿海广东、 广西和福建等地， MAR较高， POD不高、 FAR也较低， 但TS评分却相对较高， 能更好地反映年暴雨发生频次较多情况下模式对暴雨的预报性能。
图7 2022年中国区域水量R≥50.0 mm的检验评分（a）发生次数， （b） 漏报率MAR， （c）命中率POD， （d） TS评分

Fig.7 Verification scores for precipitation R≥ 50.0 mm in China's regional in 2022.（a） the number of occurrences， （b） MAR， （c） POD， （d） TS score

暴雨漏报可能会造成较大的影响， 但当预报和观测差异较小的情况下， 预报仍然有重要价值。虽然在阈值范围命中， 但数值差异较大， 应该在评分上给以“惩罚”， ITS0遵从这一原则。图8给出了ITS0评分的空间分布， 由于漏报等价影响CI是在C的基础上开展， 其基准值为1， 只有当预报和观测差值小于1.0 mm， ITS0才可能大于TS， 因此在大多数情况下， ITS0都小于TS。ITS0的空间分布显示［图8（a）］， 华南沿海ITS0相对于TS评分显著降低， 最大差值超过-0.2， 图7分析表明模式在这些地方存在较多漏报， ITS0则更好地表明了对于这些漏报事件来说， 预报和观测降水量的数值差异较大。ITS0在西北地区东部、 华中和东北部分地区高于TS， 最大增加值为0.04， 表明模式在这些地区的暴雨虽然有漏报， 但其降水量和观测的差异很小， 在某种程度上来说， 可能比命中事件的降水量报得更准确， 有很好的参考应用价值。
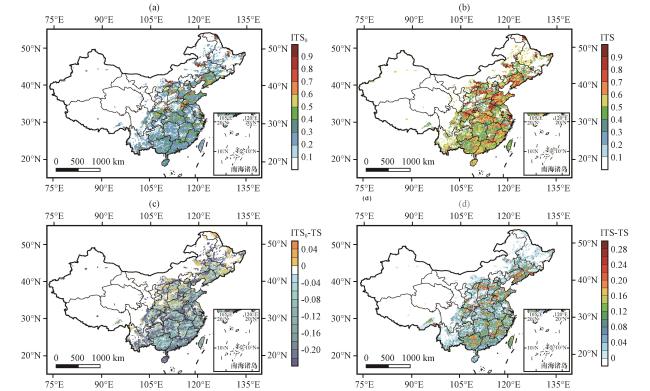
图8 2022年中国区域降水量R≥50.0 mm ECMWF模式的ITS0、 ITS以及与其TS评分的差值（a）ITS0， （b） ITS， （c） ITS0与TS评分的差值， （d） ITS与TS评分的差值

Fig.8 ITS0 scores， ITS scores， and the difference between ITS0/ITS scores and TS scores for ECMWF model forecasts with precipitation amount R≥50.0 mm in China in 2022.（a） ITS0， （b） ITS， （c） the difference between ITS0 and TS， （d） the difference between ITS and TS

R≥0.1 mm和R≥ 50.0 mm 的降水预报检验分析都表明， ITS相对于TS整体是增加的， 事实上ITS取决于AI和CI， 当命中越高的降水量级事件， 漏报事件与观测的差值越小， ITS越大， 因此， 从这一角度来看， ITS是刻画不同产品产生影响程度的很好指征。此外， 在天气预报业务中， 大量级降水在整个降水事件中的占比较低， 即使是非常好的预报， 也可能导致传统评价时采用的TS评分数值相对较低， 从而在主观预报服务中表现出降水预报能力低下， 而ITS评分很好地解决了这一问题。图8（b）显示， 尽管华南地区ITS0较低， 但ITS评分却有很好的表现， 模式能够命中大量级的降水事件， 提高模式预报的ITS评分。在华中、 华北和东北TS评分高值区， 同时也是ITS评分的高值区， 平均高于TS评分0.2， 表明模式在这些地区不仅能够更好地命中较强降水事件， 而且对于漏报事件来说， 其降水量级和观测差值也相对较小。
模式在中国西部、 青藏高原降水预报频次显著偏多（Pan et al， 2024）， 一些研究表明， 由于缺乏观测数据并且气候/天气模型对青藏高原及其周边地区的多尺度地形影响描述不足， 模型对大地形的影响的物理机制需要进一步改进（Wu et al， 2020； Wang et al， 2020）。在历史气候模拟中， 与长期平均值相比， 一些模型对降水量进行了过度估计， 超过30%~40%。从2022年ECMWF的R≥0.1 mm降水预报频次来看， 中国西部和青藏高原Bias异常偏高， 由于这些地方FAR高， 采用影响因子AI和CI后， Bias空间变化不明显。而在中国的中东部采用影响因子后， Bias明显减小， 特别是在西南和华南地区， 非常接近于1， 表明考虑降水实际量级后， 这些地方预报检验更加合理。R≥50.0 mm降水主要在东部， Bias空间上波动很大， 但从平均来看， 考虑影响因子前后， 三者的Bias分别为1.05、 1.07和0.97， 考虑AI和CI影响后， ITS对应的Bias有所减小， 在实际预报业务中， 由于空间位置预报偏差以及暴雨可能产生的灾害后果， Bias一般会增加一些， 从考虑影响因子后的Bias来看， 虽然数值变化较小， 但也说明了这一趋势。
图9 R≥0.1 mm（a、 c、 e）和R≥50.0 mm（b、 d、 f）的预报偏差（a）、 （b）为TS评分对应的Bias， （c）、 （d）为考虑等价影响AI后ITS0对应的Bias， （e）、 （f）为考虑等价影响AI和CI后对应的Bias

Fig.9 Bias for R≥0.1 mm（a、 c、 e） and R≥50.0 mm（b、 d、 f）.（a）， （b） represent the Bias corresponding to TS score； （c）， （d） represent the Bias corresponding to ITS0 after considering the AI； （e）， （f） represent the Bias after considering the AI and CI

6 结论与讨论

降水是天气预报中最为重要的要素， 随着计算能力的提高， 数值模式的水平分辨率越来越高， 降水预报也越来越精细。准确客观地评价降水的预报表现， 不仅能够更好地理解数值模式参数化方案、 中小尺度物理过程和模式框架对降水的捕捉能力， 而且对实际天气预报重点关注方向和防汛减灾有重要意义。TS评分是传统二分法点对点评分的一个重要指标， 除了TS评分之外， POD、 FAR、 ETS评分等一系列评分指标都用来评价降水的预报能力， 但已有采用二分法的评价指标对降水本身数值大小的考虑并不充分。对于粗分辨率模式来说， 模式的降水预报， 由于时空分辨率较低， 评分对降水数值大小并不十分敏感。但在高分辨率网格降水检验中存在诸多不足， 主要表现在一方面随着模式分辨率越来越高， 模式能够更好地捕获降水的空间细节特征， 相邻区域内的降水可能出现较大的数值差异； 另一方面气象观测站网也越来越密， 无论是预报还是观测都能够更好地表现时空降水的精细特征， 基于精细的降水预报， 也能够更好地服务于灾害性天气预报， 但从传统的二分法预报评分来说， 不区分漏报降水事件的具体情形， 阈值区间内降水量数值也无差别对待， 譬如观测出现249.0 mm的大暴雨， 预报量级分别为101.0 mm和240.0 mm， 都判定为正确， 在TS评分中具有相同的权重， 事实上， 这两种预报产生的结果和影响是完全不同的。
针对传统二分法列联表预报评分对降水检验可能产生的潜在结果刻画能力不足的问题， 提出一个基于影响的降水预报评分ITS。需要重点说明的是， 这里所说的降水影响并不是因降水而导致的直接结果， 而是因命中或漏报降水带来的潜在后果。ITS评分是在TS评分的基础上， 发展了影响因子的概念。对于降水命中事件来说， 单点的影响因子定义为： 1 + l g O； 对于漏报降水事件来说， 单点影响因子定义为： 1 + l g ( O - F )， 而单独考虑漏报降水事件的影响评分ITS0视作ITS的一个子项。这样定义的优点在于， 可以评价限定阈值条件下的降水预报表现， 也可以评价降水预报作为一个整体的预报表现。
基于一个假想的个例和ECMWF模式对中国2022年的降水预报， 分析ITS0和ITS特性， 并考察其与传统预报评分的差异， 结果表明， 在大多数情况下， ITS0都小于TS。ITS0高于TS表明模式对超过阈值的降水量虽然有漏报， 但差异很小， 对实际预报仍然有很强的指示意义。ITS一方面刻画了漏报事件与观测的差值大小， 另一方面反映了命中降水事件的大小差异。ITS的另一种解释可以认为， 实际发生的不同量级的降水可能产生不同的影响， 而ITS评分是不同降水产品对不同量级降水潜在后果的刻画， 某个降水预报对大量级降水的命中越好， 漏报事件与观测的误差越小， ITS评分越大， 从而这个降水预报产品就更好地反映了降水实际产生的影响。
分析中国区域2022年ECMWF模式的单向阈值暴雨的ITS0和ITS评分， 结果发现， 东南沿海ITS0显著低于TS， 而在华中、 华北和东北的部分地方ITS0有提升； 同时模式在这些地区命中满足阈值的降水事件的数值更大， 是ITS评分的高值区， 因此模式对这些地区真实降水可能产生的结果的刻画能力更好。从应用的实例来看， 虽然ITS0视为ITS的子项， 但也可以独立应用， 以此重点针对漏报事件开展分析， 具体选择ITS0或ITS， 可以根据场景和需求甄别选择。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
Ahijevych D， Gilleland E， Brown B G， et al， 2009.Application of spatial verification methods to idealized and NWP-gridded precipitation forecasts［J］.Weather and Forecasting， 24（6）： 1485-1497.

Alexander L V， Zhang X， Peterson T C， et al， 2006.Global observed changes in daily climate extremes of temperature and precipitation［J］.Journal of Geophysical Research， 111（D5）： D05109.DOI： 10.1029/2005JD006290 .

Baldwin M E， Kain J S， 2006.Sensitivity of several performance measures to displacement error， bias， and event frequency［J］.Weather and Forecasting， 21（4）： 636-648.DOI： 10.1097/01.blo.0000203478.27044.9a .

Brill K， Mesinger F， 2009.Applying a General Analytic Method for Assessing Bias Sensitivity to Bias-Adjusted Threat and Equitable Threat Scores［J］.Weather and Forecasting， 24（6）： 1748-1754.DOI： DOI： 10.1175/2009WAF2222272.1 .

Ebert E， Wilson L， Weigel A， et al， 2013.Progress and challenges in forecast verification［J］.Meteorological Applications， 20（5）： 130-139.DOI： 10.1002/met.1392 .

Ebert E， 2010.Fuzzy verification of high-resolution gridded forecasts： a review and proposed framework［J］.Meteorological Applications， 15（1）： 51-64.DOI： https： //doi.org/10.1002/met.25 .

Finley J P， 1884.Tornado predictions［J］.American Meteorological Journal， 1： 85-88.

Gillbert G F， 1884.Finley’s Tornado predictions［J］.American Meteorological Journal， 1： 166-172.

Gilleland E， Ahijevych D A， Brown B G， et al， 2010.Verifying forecasts spatially［J］.Bulletin of the American Meteorological Society， 91（10）： 1365-1373.DOI： https： //doi.org/10.1175/2010BAMS2819.1 .

Gilleland E， Ahijevych D， Brown B， et al， 2009.Intercomparison of spatial forecast verification methods［J］.Weather and Forecasting， 24（5）： 1416-1430.DOI： https： //doi.org/10.1175/2009WAF2222225.1 .

Jones C， Waliser D E， Lau K M， et al， 2004.Global occurrences of extreme precipitation and the madden-julian oscillation： observations and predictability［J］.Journal of Climate， 17， 23： 4575-4589.DOI： https： //doi.org/10.1175/3238.1

Mason I， 1989.Dependence of the critical success index on sample climate and threshold probability ［J］.Australian Meteorological Magazine， 37： 75-81.1.

Mason S J， 2004.On using climatology as a reference strategy in the Brier and ranked probability skill scores［J］.Monthly Weather Review， 132： 1891-1895.DOI： https： //doi.org/10.1175/1520-0493（2004）132<1891： OUC AAR>2.0.CO； 2 .

Mass C， Ovens D， Westrick K， et al， 2002.Does increasing horizontal resolution produce more skillful forecasts？［J］Bulletin of the American Meteorological Society， 83（3）： 407-430.DOI： https： //doi.org/10.1175/1520-0477（2002）083<0407： DIHRPM>2.3.CO； 2 .

Pan L J， Zhang H F， Mian L， et al， 2024.Assessment of ECMWF's precipitation forecasting performance for China from 2017 to 2022［J］.Journal of Tropical Meteorology， 2024， 30（3）： 257-274.DOI： 10.3724/j.1006-8775.2024.023 .

Schaefer J T， 1990.The critical success index as an indicator of warning skill［J］.Weather and Forecasting， 5（4）： 570-575.DOI： https： //doi.org/10.1175/1520-0434（1990）005<0570： TCSIAA>2.0.CO； 2 .

Sprenger M， Schemm S， Oechslin R， et al， 2017.Nowcasting foehn wind events using the AdaBoost machine learning algorithm［J］.Weather and Forecasting， 32（5）： 1079-1099.DOI： https： //doi.org/10.1175/WAF-D-16-0208.1 .

Wang Y， Yang K， Zhou X， et al， 2020.Synergy of orographic drag parameterization and high resolution greatly reduces biases of WRF-simulated precipitation in central Himalaya［J］.Climate Dynamics， 54（1）： 1729-1740.DOI： 10.1007/s00382-019-05080-w .

Wu Z P， Chen J， Zhang H B， et al， 2020.A combined verification method for predictability of persistent heavy rainfall events over East Asia based on ensemble forecast［J］.Journal of Tropical Meteorology， 26（1）： 35-46.DOI： 10.16555/J.1006-8775. 2020. 004 .

毕宝贵， 代刊， 王毅， 等， 2016.定量降水预报技术进展［J］.应用气象学报， 27（5）： 534-549.DOI： 10.11898/1001-7313.20160503.Bi B G ，

Dai K， Wang Y， et al， 2016.Advances in techniques of quantitative precipitation forecast［J］.Journal of applied Meteorological Science， 27（5）： 534-549.DOI： 10.11898/1001-7313.20160503 .

代刊， 朱跃建， 毕宝贵， 2018.集合模式定量降水预报的统计后处理技术研究综述［J］.气象学报， 76（4）： 493-510.DOI： 10.11676/qxxb2018.015.Dai K ，

Zhu Y J， Bi B G， 2018.The review of statistical post-process technologies for quantitative precipitation forecast of ensemble prediction system［J］.Acta Meteorologica Sinica， 76（4）： 493-510.DOI： 10.11676/qxxb2018. 015 .

董晓云， 余锦华， 梁信忠， 等， 2020.CWRF模式极端降水模拟误差订正［J］.应用气象学报， 31（4）： 504-512.DOI： 10.11898/1001-7313.20200412.Dong X Y ，

Yu J H， Liang X Z， et al， 2020.Bias correction of summer extreme precipitation simulated by CWRF model［J］.Journal of Applied Meteorological Science， 31（4）： 504-512.DOI： 10.11898/1001-7313.20200412 .

郭大梅， 潘留杰， 李明娟， 等， 2022.关中北部一次暴雨水汽条件及不稳定分析［J］.高原气象， 41（6）： 1481-1491.DOI： 10.7522/j.issn.1000-0534.2021.00090.Guo D M ，

Pan L J， Li M J， et al， 2022.Water vapor condition and instability analysis of a rainstorm in Northern Guanzhong［J］.Plateau Meteorology， 41（6）： 1481-1491.DOI： 10.7522/j.issn.1000-0534.2021.00090 .

江洁， 周天军， 张文霞， 2022. 近 60 年来中国主要流域极端降水演变特征［J］.大气科学， 46（3）： 707-724.DOI： 10.3878/j.issn.1006-9895.2111.21187.Jiang J ，

Zhou T J， Zhang W X， 2022.Temporal and spatial variations of extreme precipitation in the main river basins of China in the past 60 years ［J］.Chinese Journal of Atmospheric Sciences， 46（3）： 707-724.DOI： 10.3878/j.issn.1006-9895.2111.21187 .

梁旭东， 夏茹娣， 宝兴华， 等， 2022.2021年7月河南极端暴雨过程概况及多尺度特征初探［J］.科学通报， 67： 997-1011.DOI： 10.1360/TB-2021-0827.Liang X D ，

Xia R D， Bao X H， et al， 2022.Preliminary investigation on the extreme rainfall event during July 2021 in Henan Province and its multi-scale processes ［J］.Chinese Science Bulletin， 67： 997-1011.DOI： 10.1360/TB-2021-0827 .

刘静， 任川， 赵梓淇， 等， 2022.多区域高分辨率模式强降水预报检验分析［J］.气象， 48（10）： 1292-1302.DOI： 10.7519/j.issn.1000-0526.2022.050502.Liu J ，

Ren C， Zhao Z Q， et al， 2022.Comparative analysis on verification of heavy rainfall forecasts in different regional models［J］.Meteorological Monthly， 48（10）： 1292-1302.DOI： 10.7519/j.issn.1000-0526.2022.050502 .

刘侃， 陈超辉， 陈祥国， 等， 2024.一次高原地区强降水过程的对流可分辨尺度集合预报评估［J］.高原气象， 43（2）： 353-365.DOI： 10.7522/j.issn.1000-0534.2023.00066.Liu K ，

Chen C H， Chen X G， et al， 2024.Evaluation of convective-scale ensemble forecast for a severe precipitation event in the Plateau Region［J］.Plateau Meteorology.43（2）： 353-365.DOI： 10.7522/j.issn.1000-0534.2023.00066 .

刘雨萌， 赵林， 李照国， 等， 2025.一种偏差校正方法在青藏高原夏季CMIP6降水数据订正中的应用评估［J］.高原气象， 44（1）： 16-31.DOI： 10.7522/j.issn.1000-0534.2024.00046.Liu Y M ，

Zhao L， Li Z G， et al， 2025.Application evaluation of a bias correction method in the correction of CMIP6 precipitation data for summer in Qinghai-Xizang Plateau［J］.Plateau Meteorology， 44（1）： 16-31.DOI： 10.7522/j.issn.1000-0534.2024.00046 .

潘留杰， 代刊， 张宏芳， 等 ， 2024b.邻域法在天气预报中的应用研究进展［J］.大气科学学报， 47（6）： 962-975.DOI： 10.13878/j.cnki.dqkxxb.20231207001.PanL J ， DaiK， ZhangH F， et al， 2024.DOI： 10.13878/j.cnki.dqkxxb. 20231207001.Application and research progress of the neighborhood method in weather forecasting［J］.Transactions of Atmospheric Sciences， 47（6）： 962-975.DOI： 10.13878/j.cnki.dqkxxb.20231207001 .

潘留杰， 张宏芳， 刘嘉慧敏， 等 ， 2024a.MODE检验在天气预报中的应用研究进展［J］.地球科学进展， 39（2）： 193-206.DOI： 10.11867/j.issn.1001-8166.2024.012.Pan L J ， ZhangH F， LiuJ H， et al， 2024a.Advancements in study on the application of MODE Verification method in weather forecasting［J］.Advances in Earth Science， 39（2）： 193-206.DOI： 10.11867/j.issn.1001-8166.2024.012 .

潘留杰， 张宏芳， 刘静， 等， 2023.智能网格SCMOC及多模式降水预报对比［J］.大气科学学报， 46（2）： 217-229.DOI： 10.13878/j.cnki.dqkxxb.20220213001.Pan L J ，

Zhang H F， Liu J， et al， 2023.Comparative analysis of SCMOC and various numerical models for precipitation forecasting［J］.Transactions of Atmospheric Sciences， 46（2）： 217-229.DOI： 10.13878/j.cnki.dqkxxb.20220213001 .

潘旸， 谷军霞， 宇婧婧， 等， 2018.中国区域高分辨率多源降水观测产品的融合方法试验［J］.气象学报， 76（5）： 755-766..DOI： 10.11676/qxxb2018.034.Pan Y ，

Gu J X， Yu J J， et al， 2018.Test of merging methods for multi-source observed precipitation products at high resolution over China［J］.Acta Meteorologica Sinica， 76（5）： 755-766.DOI： 10.11676/qxxb2018.034 .

肖颖， 庞轶舒， 马振峰， 等， 2023.NCEP CFSv2模式对川渝夏季降水次季节预测技巧评估及预报偏差分析［J］.高原气象， 42（6）： 1576-1588.DOI： 10.7522/j.issn.1000-0534.2023.00007.Xiao Y ，

Pang Y S， Ma Z F， et al， 2023.Sub-seasonal Forecasting skills assessment and deviation analysis of CFSv2 for summer precipitation in Sichuan and Chongqing［J］.Plateau Meteorology， 42（6）： 1576-1588.DOI： 10.7522/j.issn.1000-0534.2023.00007 .

谢泽明， 余晔， 董龙翔， 等， 2024.Fitch风电场参数化方案入流风速的校正及效果检验［J］.高原气象， 43（3）： 790-801.DOI： 10.7522/j.issn.1000-0534.2023.00077.Xie Z M ，

Yu Y， Dong L X， et al， 2024.Correction and validation of the Inflow wind speed of the fitch wind farm pa-rameterization［J］.Plateau Meteorology， 43（3）： 790-801.DOI： 10.7522/j.issn.1000-0534.2023.00077 .

徐珺， 李如梦， 张庆红， 等， 2022.从大尺度环流解读河南“21·7”特大暴雨事件的极端性［J］.中国科学： 地球科学， 52（10）： 1873-1886， DOI： 10.1360/N072022-0025.Xu J ，

Li R， Zhang Q H， et al， 2022， Extreme large-scale atmospheric circulation associated with the “21·7” Henan flood［J］.Science China Earth Sciences， 65（10）： 1847-1860.DOI： 10.1007/s11430-022-9975-0 .

薛春芳， 潘留杰， 2016.基于MODE方法的日本细网格模式降水预报的诊断分析［J］.高原气象， 35（2）： 406-418.DOI： 10. 7522/j.issn.1000-0534.2015.00010.Xue C F ，

Pan L J， 2016.Diagnostic analysis of precipitation forecasting from Japan Thin-Grid Model based on MODE［J］.Plateau Meteorology， 35（2）： 406-418.DOI： 10.7522/j.issn.1000-0534.2015.00010 .

张宏芳， 潘留杰， 卢珊， 等， 2021.基于时域对象的网格降水预报的追踪诊断分析［J］.高原气象， 40（3）： 559-568.DOI： 10.7522/j.issn.1000-0534.2020.00021.Zhang H F ，

Pan L J， Lu S， et al， 2021.Tracking diagnosis analysis of grid precipitation forecast based on time-domain object［J］.Plateau Meteorology， 40（3）： 559-568.DOI： 10.7522/j.issn.1000-0534.2020.00021 .

张宏芳， 潘留杰， 杨新， 2014.ECMWF、 日本高分辨率模式降水预报能力的对比分析［J］.气象， 40（4）： 424-432.DOI： 10.7519/j.issn.1000-0526.2014.04.004.Zhang H F ，

Pan L J， Yang X， 2014.Comparative analysis of precipitation forecasting capabilities of ECMWF and Japan high resolution models［J］.Meteorological Monthly， 40（4）： 424-432.DOI： 10.7519/j.issn.1000-0526.2014.04.004 .

张夕迪， 胡艺， 张芳， 等， 2023.华北地区两次低涡暴雨过程降水特征和成因对比分析［J］.大气科学， 47（5）： 1593-1610.DOI： 10.3878/j.issn.1006-9895.2212.22060.Zhang X D ，

Hu Y， Zhang F， et al， 2023.Comparative study of the characteristics and causes of two low-vortex heavy rain events in North China［J］.Chinese Journal of Atmospheric Sciences， 47（5）： 1593-1610.DOI： 10.3878/j.issn.1006-9895.2212.22060 .

Options
文章导航

/

〈 〉

本系统由北京玛格泰克科技发展有限公司设计开发 技术支持：support@magtech.com.cn