高原气象

高原气象 >

2025 , Vol. 44 >Issue 3: 823 - 832

DOI: https://doi.org/10.7522/j.issn.1000-0534.2024.00099

基于深度学习的多气象要素影响的供热负荷预测模型研究

  • 苗芮 , 1, 2 ,
  • 李明财 , 1, 2 ,
  • 孙玫玲 1, 2 ,
  • 潘迪 3 ,
  • 张希帆 3
展开
  • 1. 天津市海洋气象重点实验室，天津 300074
  • 2. 天津市气象科学研究所，天津 300074
  • 3. 天津市气象服务中心，天津 300074
李明财（1976 -）， 男， 吉林抚松人， 正高级工程师， 主要从事城市气象服务研究. E-mail：

苗芮（1991 -）， 女， 甘肃武威人， 工程师， 主要从事供热气象服务研究. E-mail：

收稿日期: 2024-04-15

  修回日期: 2024-11-14

  网络出版日期: 2025-05-12

基金资助

天津市重点研发计划项目(21YFSNSN00130)

天津市气象局科研项目(202225ybxm12)

收起

Research on Heating Load Prediction Model based on the Influence of Multiple Meteorological Elements using Deep Learning

  • Rui MIAO , 1, 2 ,
  • Mingcai LI , 1, 2 ,
  • Meiling SUN 1, 2 ,
  • Di PAN 3 ,
  • Xifan ZHANG 3
Expand
  • 1. Tianjin Key Laboratory of Marine Meteorology，Tianjin 300074，China
  • 2. Tianjin Institute of Meteorological Science，Tianjin 300074，China
  • 3. Tianjin Meteorological Service Center，Tianjin 300074，China

Received date: 2024-04-15

  Revised date: 2024-11-14

  Online published: 2025-05-12

Copyright

© Editorial Department of Plateau Meteorology （CC BY-NC-ND）
Fold

摘要

准确的供热负荷预测对于提高集中供热系统能效和建筑物室内舒适度尤为重要。本研究以中国北方大城市天津为案例， 利用2021 -2022年采暖季实测小时供热负荷和气象观测数据， 分析了气温、风速、相对湿度和太阳辐射综合气象要素对供热负荷的影响， 并基于非线性外部输入的自回归（NARX）神经网络算法构建了一种高效的短期供热负荷预测模型。结果表明， 供热负荷具有显著的日变化及月变化特征， 与气温呈显著负相关， 与太阳辐射呈弱负相关， 与湿度、风速的相关关系有明显的季节差异。相较于仅考虑气温的供热负荷预测模型， 同时引入气温、风速、相对湿度和太阳辐射的预测模型性能最佳， 相对误差降低约1.4%。与LSTM神经网络预测模型相比， NARX神经网络模型的相对误差减少约3.6%， 有效提高了预测精度。

关键词： 气象要素; 供热负荷预测; NARX神经网络; 集中供热

本文引用格式

苗芮 , 李明财 , 孙玫玲 , 潘迪 , 张希帆 . 基于深度学习的多气象要素影响的供热负荷预测模型研究[J]. 高原气象, 2025 , 44(3) : 823 -832 . DOI: 10.7522/j.issn.1000-0534.2024.00099

Abstract

Accurate heating load forecasting is crucial for enhancing the efficiency of district heating systems and improving indoor comfort in buildings.This study takes Tianjin， a major city in northern China， as a case study.Based on hourly heating load and meteorological data from the heating season in 2021 -2022， the impacts of comprehensive meteorological factors， such as temperature， wind speed， relative humidity， and solar radiation， on heating load is analyzed.An efficient short-term heating load prediction model is constructed using the Nonlinear Autoregressive with Exogenous Inputs （NARX） neural network algorithm.The results show that the hourly heating load that displays significant diurnal and monthly variations， has a notably negative correlation with temperature， weakly negative correlation with solar radiation， while the relationships with humidity and wind speed vary depending on the season.Compared to the prediction model considering only temperature， the model incorporating temperature， wind speed， relative humidity， and solar radiation together has better prediction performance， reducing the relative error by approximately 1.4%.By comparing the forecast results with the LSTM neural network prediction model， the NARX model significantly enhances prediction accuracy with decreasing the relative error by about 3.6%.

Key words： meteorological factors; heating load prediction; NARX neural network; centralized heating

1 引言

集中供热是目前最高效、环保和经济实惠的供热方式， 中国拥有世界上最大规模的集中供热系统。作为典型的北方城市， 天津的集中供热普及率已达到99.9%（数据来源于天津市住房和城乡建设委员会）。供热负荷预测是供热行业运控调节中重要的前期工作， 准确的供热负荷预测能够减少供热供给和需求之间的差异， 降低热量损失（张文倩， 2019； 夏雨， 2019； 鹿宇， 2022； Wang et al， 2023）。优化集中供热系统的调节方法、提高供热负荷的预测精度， 实现按需供热对集中供热系统运行具有科学指导意义。
由于建筑物和社会学参数等随机因素不会在短期内发生较大变化， 因而短期供热负荷预测主要受到气象条件的影响（孙玫玲等， 2019； 全德海， 2020）。如何根据室外气象条件的变化精准调控供热， 在冷空气活动时避免供热量过低造成室内热舒适度偏低， 在气温偏高时避免供热量过高造成能源浪费， 成为十分重要的问题。室外气温的变化作为决定室内外温差及热传递的关键驱动力， 是影响供热负荷最重要的气象因子。现有研究已尝试考虑气温以外的其他气象因素， 如太阳辐射、风速等因子对供热负荷的影响， 并基于此开展供热负荷预测（Werner， 1984； Wojdyga， 2008； 张德山等， 2008； 王文标等， 2016； 张文倩， 2019）。
国内外学者应用于供热负荷预测的方法主要为建模分析、统计分析以及人工智能方法。建模分析法如反应系数法（Stephenson and Mitalas， 1967）和状态空间法（江亿， 1981）等理论方法， 以及基于以上理论研究开发的建筑动态能耗模拟软件， 包括Trnsys、Energy Plus等（Chan， 2011； 孙玫玲等， 2018， 2019）， 都是将控制理论运用到建筑负荷计算中， 基于能量守恒定律和热传递原理建立建筑热物理模型。统计分析法是基于历史数据支撑的负荷预测方法， 如利用回归分析法建立温度、太阳辐射照度与负荷的关系（Kelvin et al， 2011）， 采用多元线性回归及指数平滑法的供热负荷预测方法（Ferbar and Strmcnik， 2016）， 研究表明， 综合考虑气温、风速和太阳辐射强度等气象参数对供热负荷的影响， 负荷预测的模型精度有所提高（王文标等， 2016）。统计分析法算法比较简单， 易于获取与供热负荷有线性关系的常规影响因素。回归分析方法多为基于历史气象和供热数据建立线性函数关系， 在处理时间序列上存在一些局限性， 尤其是对动态特性和非线性关系， 以及变量之间的自相关处理能力（Liu et al， 2003）。物理建模分析法多为针对建筑物的热负荷预测模型， 如直接应用于集中供热系统， 则普适性有欠缺， 且使用固定的物理模型会降低动态供热负荷的预测精度（Li and Huang， 2013）。
近年来随着大数据和人工智能技术的发展， 机器学习和深度学习等数据驱动方法被逐渐应用于动态供热负荷的时间序列预测， 常用的方法包括支持向量回归（Zhao and Liu， 2018）、BP（Back Propagation）神经网络（王凇， 2022）、长短时记忆（Long short term memory， LSTM）神经网络（张腾达等， 2022； 张嘉益和薛贵军， 2023）算法。相比回归分析法和物理建模法， 人工智能方法在处理动态特性和非线性关系方面具备优势， 可有效提高预测精度。NARX神经网络为带有外部输入的非线性自回归神经网络模型， 适用于时间序列预测， 由输入层、输出层和多个隐含层组成， 如今逐渐被用于电力负荷预测（Hashmi， 2015； 李志新和赖志琴， 2019； 王雪菲等， 2022）、光伏发电负荷预测（Sansa et al， 2014）和供热负荷预测（Powell et al， 2014； 谢吉洋等， 2018）等能源预测领域。NARX模型因其动态反馈性质， 相较于传统机器学习方法在训练时间、参数调优及处理非线性关系的能力上具有优势（谢吉洋等， 2018）。与BP和LSTM等神经网络相比， NARX神经网络模型更适合处理时滞关系， 能够通过引入时滞的输入和输出， 更好地捕捉时间延迟， 提高对动态系统的建模和预测能力， 从而提升计算效率（王雪菲等， 2022）。短期供热负荷预测与电力负荷预测的目的一样， 旨在合理安排能源供给并提高能源利用效率， 以满足需求和降低成本， 且负荷与当前时刻及之前一段时间内的气象参数和负荷均有关系， 存在时滞性。研究表明， 使用NARX模型预测美国得克萨斯州的某校园能源系统的供热和电力负荷时， 考虑天气和时间变量后， 供热负荷的预测效果优于电力负荷（Powell et al， 2014）。
目前NARX神经网络模型在中国北方地区燃气集中供热系统的负荷预测应用相对较少， 为获取最优的短期燃气供热负荷预测模型， 本研究利用天津市气象局的气象自动站观测数据和供热企业实测的供热负荷数据， 首先分析多个气象要素对供热负荷的影响， 为模型输入变量的选取做准备； 其次， 运用NARX神经网络算法构建短期供热负荷预测模型， 通过评估检验确定最优的模型结构， 并将其预测结果与相同数据支持下的LSTM预测模型进行对比， 以期用最优的供热负荷预测模型提升供热行业科学运行水平， 助力节能减排。

2 资料来源与方法介绍

2.1　资料来源

本文用到的供热数据来源于天津市静海区某供热企业， 包括2021年11月1日至2022年3月31日（北京时， 下同）的逐小时供热负荷数据， 数据缺测率为0.1%， 识别到异常数据占比为0.4%； 用到的气象数据来自天津市气象信息中心， 采用天津市静海区国家基本气象站逐小时观测数据， 包括逐小时平均气温（单位： ℃）、平均相对湿度（单位： %）、平均2 min风速（单位： m·s-1）以及总辐射辐照度（单位： W·m-2）， 数据均经过严格的质量控制。

2.2　研究方法

2.2.1　供热负荷数据预处理

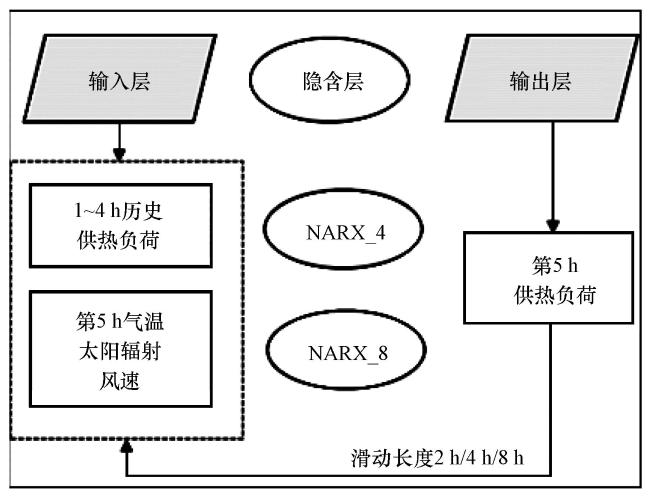
数据的准确性会直接影响对供热负荷和气象因素的相关性研究及预测模型的建立。在供热数据采集中， 由于人为错误和系统故障， 可能导致历史供热负荷数据异常。因而在研究开始前， 需要对异常数据进行预处理， 包括检查数据的一致性、处理无效值和缺失值等。
首先识别异常数据， 包括： （1）序列中的缺测值； （2）与相邻时段数据差别较大的异常数据； （3）供热站工作日志中记录的异常数据。然后对异常数据进行处理， 在本研究中主要是通过相邻数据的平均值来修正或补全异常数据。

2.2.2　 NARX神经网络模型数据集构建

为了考察气温、风速、湿度、太阳辐射对供热负荷的影响， 构建数据集如表1所示。在逐时供热负荷的模型建立过程中， 考虑到气象要素的季节变化， 故选择每月序列的前80%为训练集， 后20%为测试集。
表1 多要素数据集

Table 1 Multi-factor datasets

数据集 历史供热负荷 平均气温 太阳辐射 平均风速 相对湿度
数据集A ○ ○ × × ×
数据集B ○ ○ ○ × ×
数据集C ○ ○ × ○ ×
数据集D ○ ○ × × ○
数据集E ○ ○ ○ ○ ×
数据集F ○ ○ ○ × ○
数据集G ○ ○ × ○ ○
数据集H ○ ○ ○ ○ ○

“○”表示该数据集包含该要素， “×”表示该数据集不包含该要素（'○' indicates that the dataset contains the element； '×' indicates that the dataset does not contain the element）

2.2.3　 NARX神经网络模型训练数据归一化处理

使用神经网络模型进行多变量预测时， 因为不同变量的量纲不同， 数值差异较大， 会影响模型中激活函数的输入输出范围， 从而导致损失函数无法正常工作。因此需要对各变量进行归一化处理， 以平等考虑各变量对供热负荷的影响。本研究中采用极值归一化方法， 将各变量的数值归算到区间［0， 1］内， 公式为：
x ' = x - x m i n x m a x - x m i n
式中： x '为归一化后的样本数据； x为原始样本数据； x m i n， x m a x分别代表样本时间序列的最小值和最大值。

2.2.4　 NARX神经网络模型训练步骤及参数设置

为了确定滑动窗口长度对预测性能的影响， 连续2 h\4 h\8 h历史供热负荷数据分别组成历史数据向量， 并结合气温等气象因子形成数据集（见表1）， 随后进行NARX神经网络模型训练。模型训练输入输出的示意如图1所示， 如当滑动窗口为4 h， 滑动步长为2 h（默认滑动步长为滑动窗口的一半）， 输入数据集E， 则第一次训练时输入第1~4 h的历史供热负荷、第5 h的气温、太阳辐射和风速， 第5 h的供热负荷作为输出； 第二次训练时输入第3~6 h的历史供热负荷、第7 h的气温、太阳辐射和风速， 第7 h的供热负荷作为输出； 以此类推， 直到全部数据用于模型训练。
图1 NARX神经网络模型训练示意图

Fig.1 Diagram of the training process of the NARX neural network model

为了研究滑动窗口长度和隐含层数量对供热负荷预测精度的影响， 本文提出6个模型（见表2）， 每个模型分别用表1中的数据集A-H进行10次训练和验证， 共计480组实验， 以分析供热负荷预测的误差分布情况。
表2 不同模型对应的滑动窗口长度和隐含层数量

Table 2 Sliding window length and number of hidden layers for different hourly models

滑动窗口长度/h 4隐含层 8隐含层
2 NARX2_4 NARX2_8
4 NARX4_4 NARX4_8
8 NARX8_4 NARX8_8

2.2.5　 NARX神经网络模型评估方法

为了评估供热负荷预测模型的性能， 采用均方根误差（Root Mean Squared Error， RMSE）、平均绝对误差（Mean Absolute Error， MAE）和对称平均绝对百分比误差（Symmetric Mean Absolute Percentage Error， SMAPE）作为评估标准， 评估预测模型的准确性， 计算公式如下所示：
R M S E = 1 n ∑ i = 1 n ( y i - y p i ) 2
M A E = 1 n ∑ i = 1 n | y p i - y i |
S M A P E = 100 % n ∑ i = 1 n | y p i - y i | ( | y p i | + | y i | ) / 2
式中： y i为实际供热负荷值； y p i为模型预测值； n为模型训练的滑动步长。采用学生t检验对评估计算值进行检验。

3 结果分析

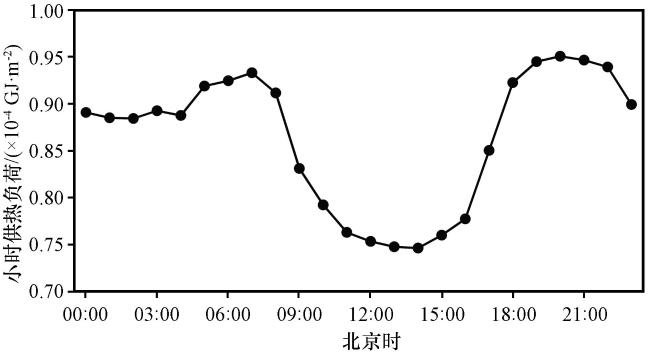
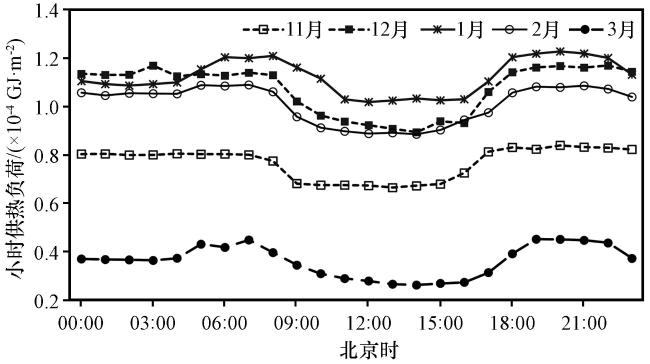
3.1　供热负荷的时间特征分析

图2表示2021 -2022年采暖季逐小时单位面积供热负荷的日变化， 供热负荷表现出显著的日变化特征。其中， 20:00 -21:00供热负荷达到峰值0.95×10-4 GJ·m-2， 次高峰出现在22:00和07:00， 为0.93×10-4 GJ·m-2； 而最低值出现在12:00 -14:00， 为0.75×10-4 GJ·m-2。具体变化趋势表现为， 20:00 - 08:00期间， 由于气温较低， 供热负荷维持在较高水平， 20:00 -04:00逐渐下降， 随后在04:00 - 07:00回升； 07:00 -14:00， 随着气温升高， 供热负荷逐渐降低， 并在12:00 -14:00达到最低点； 14:00 - 20:00， 随着气温下降， 供热负荷再次增大。
图2 2021 -2022年采暖季逐小时单位面积供热负荷的日变化

Fig.2 Daily variation of hourly unit area heating load during 2021 -2022 heating season

由于气象要素具有显著的季节变化特征， 因而需进一步考察供热负荷的季节变化。图3展示了2021 -2022年采暖季各月的供热负荷日变化特征， 可见， 各月供热负荷均呈现出显著的日变化特征， 夜间供热负荷较高， 而白天尤其是10:00 -15:00较低。对比各月的日变化特征， 发现2月和12月的日变化特征最为显著， 而1月的日变化特征最不明显。
图3 2021 -2022年采暖季各月的逐小时单位面积供热负荷的日变化（单位： ×10-4 GJ·m-2）

Fig.3 Daily variation of hourly unit area heating load for each month during the 2021 -2022 heating season.Unit： ×10-4 GJ·m-2

3.2　供热负荷与气象因子的相关分析

为了探究逐时供热负荷与各气象因子的关系， 进一步分析采暖季各月逐时供热负荷与气象要素的相关性。如表3所示， 各月供热负荷均与平均气温表现出显著的负相关关系， 其中， 2月和12月相关性最高， 11月次之， 而1月相关性最弱， 这与图3中负荷日变化特征的逐月差异类似。
表3 2021 -2022年采暖季各月逐小时气象要素和供热负荷的相关关系

Table 3 Correlations between hourly meteorological factors and heating load for each month during the 2021 -2022 heating season

月份 平均气温 相对湿度 太阳辐射 平均风速
11月 -0.659* -0.154* -0.204* 0.122*
12月 -0.711* -0.122* -0.360* 0.008
1月 -0.343* 0.325* -0.304* -0.135*
2月 -0.763* 0.333* -0.303* -0.272*
3月 -0.574* 0.079* -0.310* -0.160*

*表示通过 α = 0.05的显著性检验（* indicates statistical significance at α=0.05）

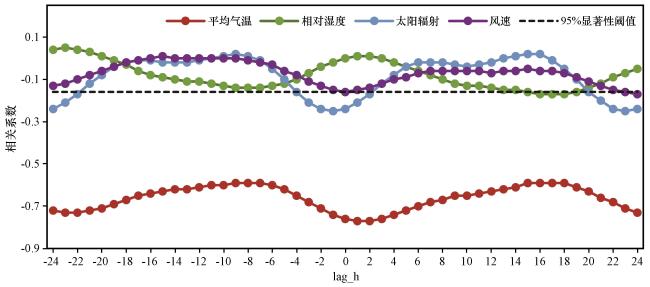
此外， 太阳辐射与供热负荷在各月均呈弱的负相关。相对湿度和风速与负荷表现出弱相关关系， 其中， 相对湿度在1 -2月与供热负荷呈弱正相关， 11 -12月弱负相关； 平均风速在1 -3月与供热负荷呈弱负相关。
以上对逐小时供热负荷和气象要素的相关分析均为同时相关， 为了考察气象要素与供热负荷的时滞相关关系， 图4展示了2021 -2022年采暖季整体逐小时供热负荷与各气象要素的时滞相关系数。可以看出， 气温在超前24 h到滞后24 h范围内与供热负荷始终存在显著的负相关关系， 且在滞后1~2 h以及同时相关性最强。除气温外， 太阳辐射在超前和滞后20~24 h、以及超前3 h到滞后1 h期间呈弱负相关关系。
图4 2021 -2022年采暖季逐小时供热负荷与各气象要素的时滞相关系数

其中横坐标表示超前24 h到滞后24 h， 0表示同时相关， 黑色虚线表示95%显著性检验的临界值

Fig.4 The lagged correlation coefficients of hourly heating load with various meteorological factors during the 2021 -2022 heating season.The horizontal axis represents a range from 24 hours ahead to 24 hours behind， with 0 indicating simultaneous correlation， and the black dashed line indicating the threshold for the 95% significance test

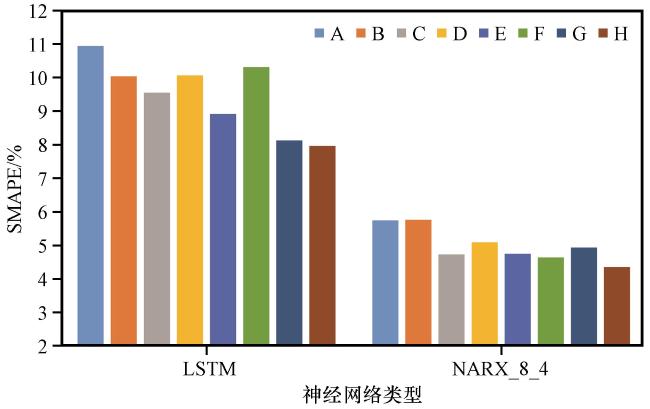
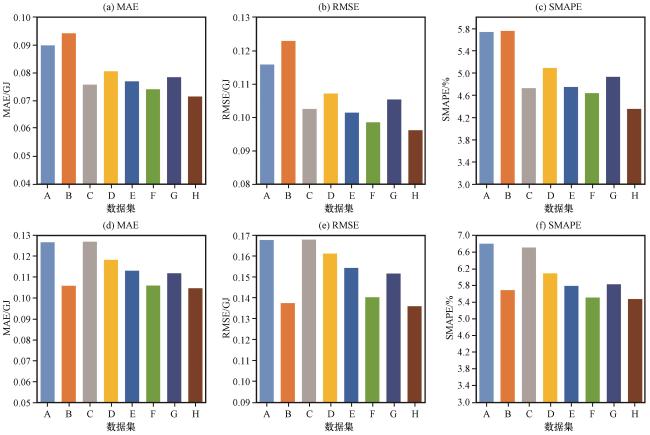
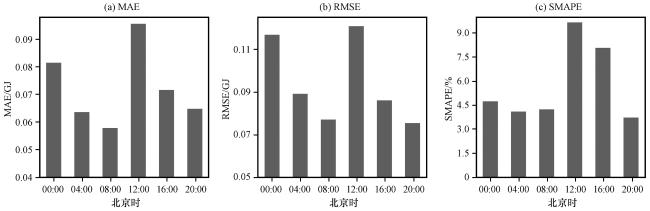
综上所述， 逐时供热负荷呈显著的日变化特征， 20:00和21:00达到峰值， 中午时段则最低。各月对比显示， 2月和12月供热负荷的日变化特征最为显著， 1月则最不明显。供热负荷与平均气温呈显著负相关， 与太阳辐射呈弱负相关， 而相对湿度和风速与供热负荷的相关性因月份而异， 总体较弱。时滞相关分析表明， 供热负荷与气温在滞后1~2 h及同时的相关性最强。总体来看， 供热负荷与气象因子的关系具有明显的季节差异。

3.3　供热负荷预测模型实验结果

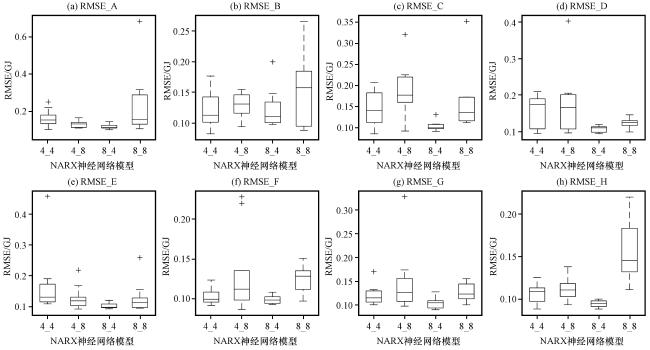
通过训练和验证供热负荷预测的每个模型， 共得到480组实验结果， 其RMSE、MAE、SMAPE指标的箱线图如图5~7所示（为了更好地比较结果， 仅展示滑动窗口为4 h和8 h的实验结果， 因滑动窗口2 h的模型误差分布较为分散， 并存在较多异常值； 图5~7中（a）~（h）分别代表输入数据集A至数据集H， 包含了不同的要素， 其中数据集A表示仅输入历史供热负荷和平均气温， 数据集H表示输入历史供热负荷、平均气温、风速、相对湿度和太阳辐射， 具体见表1， 横坐标X_Y表示不同的滑动窗口X和隐含层数Y的NARX神经网络模型）。结果显示， 滑动窗口长度为8 h且隐含层数为4层的NARX神经网络预测模型（NARX_8_4）在大多数数据集上的评价指标的分布最为集中， 并具有最小的中位数。因此， 可以得出“NARX_8_4”模型为逐小时负荷预测的最佳模型。
图5 供热负荷预测中使用不同数据集训练模型的均方根误差RMSE箱线图

Fig.5 The box plot of root mean square error RMSE for the training of the heating load models using different datasets

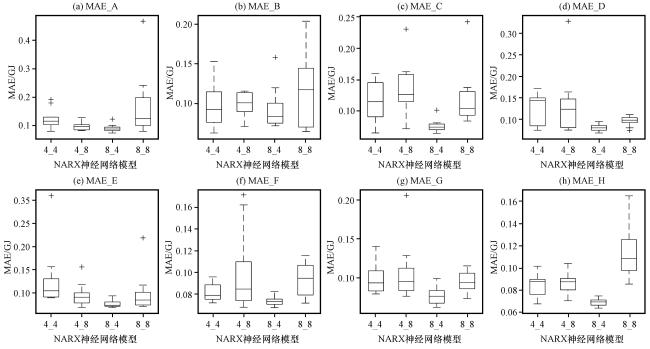
图6 供热负荷预测中使用不同数据集训练模型的平均绝对误差MAE箱线图

Fig.6 The box plot of mean absolute error MAE for the training of the heating load models using different datasets

图7 供热负荷预测中使用不同数据集训练模型的对称平均绝对百分比误差SMAPE箱线图

Fig.7 The box plot of symmetric mean absolute percentage error SMAPE for the training of the heating load models using different datasets

比较不同隐含层数的模型结果可以得出， 具有4层隐含层的模型误差评价指标略小于具有8层隐含层的模型。这可能是因为当隐含层增至8层时， NAXR神经网络存在过拟合的风险（表现为在训练集上优于测试集）。同时， 随着隐含层数的增加， 模型的训练时间会显著延长， 导致模型稳定性下降。综上所述， 本文选择了4层隐含层的NAXR神经网络。

3.4　不同气象要素数据集的供热负荷预测模型对比

为了研究在NARX神经网络模型中引入不同气象要素的影响， 给出数据集A-H对应的NARX神经网络模型预测结果与真实值的对比图（图8， 仅选取部分预测样本展示， A~H代表8个数据集， 具体见表1）。整体来看， 8个数据集的预测值相对接近， 但使用数据集H训练的模型预测偏差最小， 最接近真实值。这表明同时引入气温、风速、相对湿度和太阳辐射对供热负荷预测具有正贡献， 且误差最小， 具体而言， RMSE为0.136 GJ， MAE为0.105 GJ， SMAPE为4.4 %， 与仅考虑气温的预测模型相比， RMSE和MAE减小约0.02GJ， SMAPE减小约1.4%。
图8 2021年11月27日08:00至30日20:00供热负荷预测模型真实值与预测值对比图

Fig.8 The comparison between the original values and predicted values of the heating load models from 08:00 to 20:00 on November 27， 2021

3.5　模型比较

本节比较了最优NARX神经网络模型NARX_8_4与长短期记忆神经网络模型（LSTM）在逐时供热负荷预测中的表现。对于LSTM神经网络模型的滑动窗口同样设置为8 h， 且使用与NARX神经网络模型相同的数据集进行训练和预测。根据误差结果（图9）， LSTM模型在8个数据集上的SMAPE均大于8.0 %， 相比之下， 基于数据集H的NARX_8_4模型的相对误差较LSTM模型降低了3.6 %。
图9 LSTM和NARX_8_4神经网络模型的对称平均绝对百分比误差SMAPE对比

Fig.9 The comparison of symmetric mean absolute percentage error （SMAPE） between LSTM and NARX_8_4 neural network prediction models

4 讨论

本研究探讨了供热负荷的日变化和月变化特征以及气象因素的影响， 经过优化配置开发的NARX神经网络模型， 实现了基于综合气象因素和历史供热数据的短期供热负荷预测。基于以上研究结果， 依托天津市气象局的智能网格预报， 可通过业务平台为供热企业提供短期供热负荷预测。经该企业评估， 与传统的人工经验式调控方式相比， 该模型在节能效果和服务效率方面具有优势， 主要表现在与上年能耗相比， 基于气象相似日计算得到的节能量2%~3%； 同时， 与以往参考单一气温预报的人工调控方式相比， 基于多要素的负荷预测值（供热量）， 可以直接用于调控供水温度和流量， 使调控更为科学可靠。此外， 利用最新收集的2023 -2024年采暖季供热数据和气象观测数据构建的数据集， 输入最优NARX神经网络模型， 得到的预测结果误差如图10（d）~（f）所示， 与本研究的模型训练结果一致［图10（a）~（c）］， 即同时输入气温、风速、相对湿度和太阳辐射得到的预测结果最接近真实值。
图10 2021 -2022年采暖季（a~c）和2023 -2024年采暖季（d~f）供热负荷预测模型的评估结果对比

Fig.10 Comparison of evaluation results of heating load prediction models in 2021 -2022 heating season （a~c） and 2023 -2024 heating season （d~f）

由于供热负荷具有显著的日变化特征， 进一步分析负荷预测模型的准确率随时间的变化。图11显示了使用数据集H的NARX_8_4神经网络模型在不同时段的误差， 其中12:00误差较大， 而08:00和20:00误差相对较小。这表明模型较好的掌握了一天中负荷高峰时段的规律； 而对于负荷最低时段12:00， 模型的泛化能力相对较弱， 可能是因为供热站中午时段有时会采取降低供热量或间歇供热策略以节省能源， 增加了该时段负荷的随机性。因此， 后续应加强对分时段模型的修正， 以进一步提高模型的准确性。
图11 使用H数据集的NARX_8_4神经网络预测模型评估结果随时间的变化

Fig.11 Variation of Error over time for the NARX_8_4 neural network prediction model using the H dataset

尽管本研究取得了一定的成果， 但仍存在一些局限性。首先， 基于天津的实测数据， 模型的适用性可能受到不同地区的气候特征和供热系统运行机制的限制。因此， 未来的研究可以考虑在不同城市或地区进行模型验证， 以提高普适性。其次， 我国北方地区集中供热系统涉及多种热源， 除燃气外， 还包括地热源和热电联产等。目前针对不同热源对气象因素的响应关系研究较少， 未来研究需探讨不同热源类型的供热负荷响应特征， 以提供更具针对性的预测模型和调控策略。

5 结论

本文利用逐小时供热负荷及气象观测数据， 研究了综合气象要素对供热负荷的影响； 并采用NARX神经网络算法构建了短期供热负荷预测模型， 对模型性能进行了检验评估。结论如下：
（1） 供热负荷具有显著的日变化特征， 其中20:00和21:00达到峰值， 而12:00 -14:00则最低。不同月份供热负荷的日变化有所差异， 2月和12月最为显著， 而1月最不明显。
（2） 相关分析显示， 供热负荷与平均气温呈显著负相关， 与太阳辐射呈弱负相关， 与相对湿度、风速的相关性随季节变化。时滞相关分析表明， 供热负荷与气温在滞后1~2 h及同时的相关性最强。
（3） 通过多次训练和测试， 选择最优的滑动窗口长度及隐含层数， 构建了基于综合气象要素影响的供热负荷预测模型。结果表明， 8 h滑动窗口长度和4层隐含层的NARX神经网络模型效果最佳。
（4） 对比不同气象因素的数据集发现， 包含气温、风速、相对湿度和太阳辐射的数据集可提高供热负荷预测模型的性能， 相较于仅输入气温， 相对误差减小约1.4 %。此外， 在相同的数据条件下， NARX_8_4神经网络模型的预测误差较LSTM模型降低约3.6 %。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
Chan A L S， 2011.Developing future hourly weather files for studying the impact of climate change on building energy performance in Hong Kong［J］.Energy and Buildings， 43（10）： 2860-2868.

Ferbar T L， Strmcnik E， 2016.The comparision of Holt-winters method and multiple regression method： a case study［J］.Energy and Buildings， 109： 266-276.

Hashmi M U， Arora V， Priolkar J G， 2015.Hourly electric load forecasting using Nonlinear AutoRegressive with eXogenous （NARX） based neural network for the state of Goa， India［C］.International Conference on Industrial Instrumentation and Control， 1418-1423.

Kelvin K K W， Danny W W L， Liu D L， et al， 2011.Future trends of building heating and cooling loads and energy consumption in different climates［J］.Building and Environment， 46（1）： 223-234.

Li Z W， Huang G S， 2013.Re-evaluation of building cooling load prediction models for use in humid subtropical area［J］.Energy and Buildings， 62（3）： 442-449.

Liu R， Kuang J， Gong Q， et al， 2003.Principal component regression analysis with SPSS［J］.Computer Methods and Programs in Biomedicine， 71（2）： 141-147.

Powell K M， Akshay S， Wesley J C， et al， 2014.Heating， cooling， and electrical load forecasting for a large-scale district energy system［J］.Energy， 74： 877-885.

Sansa I， Missaoui S， Boussada Z， et al， 2014.PV power forecasting using different artificial neural networks strategies［C］.International Conference on Green Energy， Piscataway， NJ： IEEE， 2014： 54-59.

Stephenson D G， Mitalas G P， 1967.Cooling load calculation by thermal response factors［J］.ASHRAE Transaction， 73（1）： 2.

Wang Y M， Li Z W， Liu J J， et al， 2023.Data-driven analysis and prediction of indoor characteristic temperature in district heating systems［J］.Energy， 282： 129023.

Werner S， 1984.The heat load in district heating system［J］.Sweden： Chalmers Unicersity of Technology.

Wojdyga K， 2008.An influence of weather conditions on heat demand in district heating systems［J］.Energy and Buildings， 40（11）： 2009-2014.

Zhao J， Liu X J， 2018.A hybrid method of dynamic cooling and heating load forecasting for office buildings based on artificial intelligence and regression analysis.Energy and Buildings， 174： 293-308.

江亿， 1981.模拟房间热响应的新方法——状态空间法［J］.建筑技术通讯（暖通空调） （2）： 49.

Jiang Y， 1981.A new method to simulate room thermal response——State space method［J］.Building Technology Communication （2）： 49.

李志新， 赖志琴， 2019.基于NARX神经网络的电力负荷中期预测［J］.贵州农机化， 1： 26-31.

Li Z X， Lai Z Q， 2019.Medium term forecast of power load based on NARX neural network［J］.Guizhou Agricultural Mechanization， 1： 26-31.

鹿宇， 2022.热力站供热负荷预测的影响因素研究［D］.北京： 北京建筑大学.Lu Y， 2022.Study on the influencing factors of heating load forecast for thermal power station［D］.Beijing： Beijing University of Civil Engineering and Architecture.

全德海， 2020.室外温度变化与间歇供暖对值班供暖室温的影响［J］.建筑节能， 2（48）： 163-168.

Quan D H， 2020.Effect of outdoor temperature change and intermittent heating on room temperature of non-working time heating［J］.Building Energy Efficiency， 2（48）： 163-168.

孙玫玲， 李明财， 曹经福， 2018.利用采暖/制冷度日分析不同气候区建筑能耗的适用性评估［J］.气象与环境学报， 34（5）： 135-141．

Sun M L， Li M C， Cao J F， 2018.Applicability of cooling/heating degree days in evaluating building energy consumption of different climate zones［J］.Journal of Meteorology and Environment.Journal of Meteorology and Environment， 34（5）： 135-141.

孙玫玲， 袁闪闪， 张宇峰， 等， 2019.基于精细化气象预报的供热调控技术研究进展［J］.建筑科学， 35（10）： 182-190.

Sun M L， Yuan S S， Zhang Y F， et al， 2019.A review of research process in heating regulation technology based on fine meteorological forecast［J］.Building Science， 35（10）： 182-190.

王凇， 2022.基于机器学习的智慧供热负荷预测研究［D］.吉林建筑大学.Wang S， 2022.Research on intelligent heating load forecasting based on machine learning［D］.Jilin Jianzhu University.

王文标， 蔡麒， 汪思源， 2016.基于气象因素的集中供热系统热负荷预测研究［J］.计算机测量与控制， 24（2）： 22-26.

Wang W B， Cai Q， Wang S Y， 2016.Research of district heating system heat load prediction based on weather factors［J］.Computer Measurement &Control， 24（2）： 22-26.

王雪菲， 李勇， 余国晓， 等， 2022.基于DMD-NARX模型的短期电力负荷预测方法［J］.黑龙江大学自然科学学报， 39（3）： 307-316.

Wang X F， Li Y， Yu G X， et al， 2022.Short-term power load forecasting method based on DMD-NARX model［J］.Journal of Natural Science of Heilongjiang University， 39（3）： 307-316.

夏雨， 2019.基于西安实测的某集中供热系统动态分析及调控策略［D］.西安： 西安工程大学.Xia Y， 2019.Dynamic analysis and control strategy of a central heating system based on field measurement in Xi'an［D］.Xi'an： Xi'an University of Engineering.

谢吉洋， 闫冬， 谢垚， 等， 2018.基于NARX神经网络的热负荷预测中关键影响因素分析［J］.计算机应用， 38（11）： 3180-3187.

Xie J Y， Yan D， Xie Y， et al， 2018.Analysis of key factors in heat demand prediction based on NARXneural network［J］.Journal of Computer Applications， 38（11）： 3180-3187.

张德山， 王保民， 陈正洪， 等， 2008.北京市城市集中供热节能气象预报系统的应用［J］.煤气与热力， 28（11）： 23-25.Zhang D S， Wang B M， Chen Z H， et al， 2008.Application of weather forecast system for Beijing city centralized heat-supply energy-saving system［J］.Gas & Heat， 28（11）， 23-25.

张嘉益， 薛贵军， 2023.基于混合神经网络的短期供热负荷预测模型研究［J］.自动化仪表， 44（5）： 63-68.

Zhang J Y， Xue G J， 2023.Research on short-term heating load forecasting model based on hybrid neural network［J］.Process Automation Instrumentation， 44（5）： 63-68.

张腾达， 李琦， 陈波， 2022.基于LSTM的热力站短期热负荷预测研究［J］.计算机仿真， 39（9）： 507-512.

Zhang T D， Li Q， Chen B， 2022.Research on short-term heat load forecasting of thermal power station based on LSTM［J］.Computer Simulation， 39（9）： 507-512.

张文倩， 2019.基于气象因素的集中供暖系统的热负荷预测研究［D］.保定： 华北电力大学.Zhang W Q， 2019.Research on Heat load forecasting of centralized heating system based on meteorological factors［D］.Baoding： North China Electric Power University.

Options
文章导航

/

〈 〉

本系统由北京玛格泰克科技发展有限公司设计开发 技术支持：support@magtech.com.cn